Как найти массу сплава в математике

Задачи ЕГЭ на сплавы, смеси, растворы.

Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.

. В сосуд, содержащий  литров -процентного водного раствора некоторого вещества, добавили  литров воды. Сколько процентов составляет концентрация получившегося раствора?

В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .

Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:

.

. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Пусть масса первого раствора равна . Масса второго — тоже . В результате получили раствор массой . Рисуем картинку.

Получаем:

Ответ: .

. Виноград содержит  влаги, а изюм — . Сколько килограммов винограда требуется для получения  килограммов изюма?

Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось  воды, значит, «сухого вещества» было . В изюме  воды и  «сухого вещества». Пусть из кг винограда получилось  кг изюма. Тогда

 от  от 

Составим уравнение:

и найдем .

Ответ: .

. Имеется два сплава. Первый сплав содержит  никеля, второй —  никеля. Из этих двух сплавов получили третий сплав массой  кг, содержащий  никеля. На сколько килограммов масса первого сплава меньше массы второго?

Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .

Запишем простую систему уравнений:

Первое уравнение — масса получившегося сплава, второе — масса никеля.

Решая, получим, что .

Ответ: .

. Смешав -процентный и -процентный растворы кислоты и добавив  кг чистой воды, получили -процентный раствор кислоты. Если бы вместо  кг воды добавили  кг -процентного раствора той же кислоты, то получили бы -процентный раствор кислоты. Сколько килограммов -процентного раствора использовали для получения смеси?

Пусть масса первого раствора , масса второго равна . Масса получившегося раствора равна . Запишем два уравнения, для количества кислоты.

Решаем получившуюся систему. Сразу умножим обе части уравнений на , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.

Ответ: .

Задачи на смеси и сплавы — подробнее

Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.

То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.

Обычно концентрация измеряется в процентах.

Что такое процент?

Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.

Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).

Почему?

Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).

Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?

Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.

Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.

Более подробно о процентах – в темах  «Дроби, и действия с дробями»и «Проценты».

Поехали дальше.

Масса раствора, смеси или сплава равна сумма масс всех составляющих.

Логично, правда?

Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.

И еще одна очевидность:

При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.

А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.

Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.

Когда мы их смешаем, чему будет равна масса нового раствора?

( displaystyle 10+14=24) кг.

А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.

Перейдем к задачам.

Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике

ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)

В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.

Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).

Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.

Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.

Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).

ЕГЭ №17 Экономическая задача. Вклады

Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!

Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.

По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.

Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!

На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.

С самого начала моей профессиональной деятельности мне приходится искать ответ на вопрос: «Как научить решать детей различного вида задачи?». Я, думаю, что эта проблема беспокоит любого практикующего учителя, как начальной школы, так и старшей.

С введением ЕГЭ и ОГЭ данный вопрос стал еще более актуальным. Если рассмотреть учебники по которым ведется преподавание математики в наших школах, то становится понятно, что решение задач любого вида рассматривается только с одной стороны, тогда как на самом деле большую часть из них можно решать более простыми и красивыми способами.

Рассмотренные мною методы решения задач на смеси и сплавы позволяют упростить решение данного вида задач, расширить математический кругозор учащихся, развивают умение отбирать и анализировать информацию.

1. С ПОМОЩЬЮ РИСУНКА

В ходе решения различных задач я пришла к выводу, что их решать проще, если есть определенная картинка. Изображаем каждую смесь (сплав) в виде прямоугольника разбитого на фрагменты, количество которых соответствует количеству составляющих эту смесь (этот сплав) элементов.

Задача 1. Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Изобразим каждый из сплавов в виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). Кроме того, на модели отобразим характер операции — сплавление, поставим знак «+» между первым и вторым прямоугольниками. Поставив знак «=» между вторым и третьим прямоугольниками, мы тем самым показываем, что третий сплав получен в результате сплавления первых двух. Полученная схема имеет следующий вид:

Теперь заполняем получившиеся прямоугольники в соответствии с условием задачи:

1. Над каждым прямоугольником («маленьким») указываем соответствующие компоненты сплава. При этом обычно бывает достаточно использовать первые буквы их названия (если они различны). Удобно сохранять порядок соответствующих букв.
2. Внутри прямоугольников вписываем процентное содержание (или часть) соответствующего компонента. Понятно, что если сплав состоит из двух компонентов, то достаточно указать процентное содержание одного из них. В этом случае процентное содержание второго компонента равно разности 100% и процентного содержания первого.
3. Под прямоугольником записываем массу (или объем) соответствующего сплава (или компонента).

Рассматриваемый в задаче процесс можно представить в виде следующей модели-схемы:

Решение.

1-й способ. Пусть хг — масса первого сплава. Тогда, (200-х)г — масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему:

Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):

Решив это уравнение, получаем х=140. При этом значении х выражение 200-х= 60. Это означает, что первого сплава надо взять140г, а второго — 60г.

2-й способ. Пусть х г и у г — масса соответственно первого и второго сплавов, то есть пусть исходная схема имеет вид:

Легко устанавливается каждое из уравнений системы двух линейных уравнений с двумя переменными:

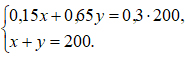
Решение системы приводит к результату: x = 140, y = 60. Значит, первого сплава надо взять 140 г, а второго — 60 г.

Ответ: 140г, 60г.

В конечном итоге задачу можно решить с помощью уравнения или системы уравнений, однако без рисунка это сделать гораздо сложнее. Стоит отметить, что решение задач на смеси и сплавы таким способом является основным и наиболее часто используемым.

2. С ПОМОЩЬЮ ПРИРАВНИВАНИЯ ПЛОЩАДЕЙ РАВНОВЕЛИКИХ ПРЯМОУГОЛЬНИКОВ

Как нам известно из курса геометрии площади равновеликих прямоугольников равны. Это свойство можно использовать при решении задач на смеси и сплавы, когда известны концентрации смешиваемых растворов, полученного раствора и масса какого-нибудь из них.

Пример: Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора. Сколько граммов каждого раствора надо было взять?

Пусть x г масса первого раствора, тогда масса второго (600 — x) г.

На горизонтальной оси отложим массы всех трех растворов, на вертикальной — процентное содержание соляной кислоты. На рисунке площадь голубого прямоугольника равна 15х, сиреневого — 5(600 — х).

15 х = 5 (600 — х)

х = 150

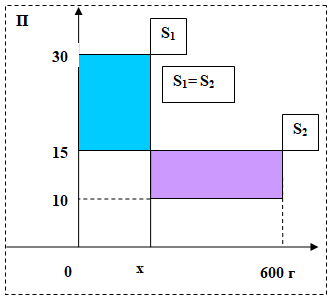
Ответ: 150г 30% и 450г 10% раствора.

При рассмотрении этого способа возникло сомнение в равновеликости полученных прямоугольников. Для доказательства этого возьмем два раствора с некоторым веществом: I — имеет a %концентрацию этого вещества, II — с %, причем с>a. При их смешивании получили раствор массой m, концентрация вещества в котором составляет b %.

Изобразим на координатной плоскости имеющиеся данные, причем массу раствора с большей концентрацией возьмем за x, тогда масса второго раствора будет (m — x).

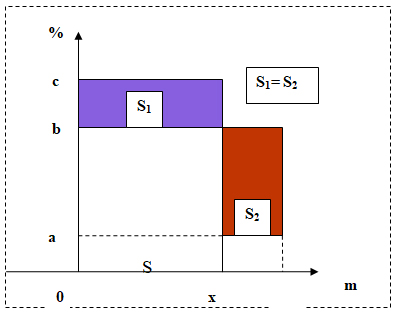
Предположим, что площади закрашенных прямоугольников равны:

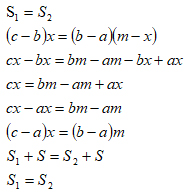
Наше предположение верно. Следовательно, данный способ можно использовать при решении задач в том случае, когда известны концентрации смешиваемых растворов, полученного раствора и масса одного из них.

3. АРИФМЕТИЧЕСКИЙ СПОСОБ РЕШЕНИЯ

При написании данной работы, я столкнулась со способом решения задач, который в разных источниках называется по-разному: арифметический, метод креста, метод рыбки, метод квадрата. Несмотря на то, что существует некоторая разница в оформлении, суть этого способа не меняется.

Любой человек понимает, что когда происходит смешивание каких либо веществ, они берутся в каком-то отношении. Суть этого метода заключается в том, что существует возможность найти в каком отношении взяты смешиваемые вещества. Так же возможно найти массу двух из веществ, если известна масса третьего.

Рассмотрим пример решения задачи. В точке начала двух отрезков обозначают концентрацию смеси. Далее указывают концентрации составных частей смеси, а справа — разности концентраций смеси и ее составных частей:

Возьмем два раствора с некоторым веществом: I — имеет a % концентрацию этого вещества, II — с %, причем с>a. При их смешивании получили раствор массой m, концентрация вещества в котором составляет b %. Исходя из предложенной схемы, получим, что вещества берутся в отношении:

РЕШЕНИЕ ЗАДАЧ МЕТОДОМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Применяется для решения задач на разбавление и смешивание растворов.

Преимущества: легко восстановить в памяти (в отличие от метода креста), решает задачу одним уравнением.

В основе метода лежит определение:

где ω — массовая доля растворенного вещества,

m в-ва — масса растворенного вещества,

m — масса раствора.

Следовательно, масса растворенного вещества равна произведению массы раствора на массовую долю растворенного вещества:

mв-ва = m · ω (2).

При сливании растворов складываются как массы растворов:

m1 + m2 = m3 (3)

так и массы растворенных веществ:

mв-ва1 + mв-ва2 = mв-ва3

Подставляя вместо массы растворенных веществ произведение (2), получаем:

m1 · ω1 + m2 · ω2= m3 · ω3

Заменяя неизвестную массу на выражение (3), получаем:

m1 · ω1 + m2 · ω2= (m1 + m2) · ω3 (4), или

m1 · ω1 + (m3 — m1) · ω2= m3 · ω3 (5)

Пример: Определите массы 10%-ного и 50%-ного (по массе) растворов, необходимые для получения 200 г 20%-ного раствора.

Решение:

ω1 = 10%, ω2 = 50%, ω3= 20%, m3 = 200 г, m2 = 200 — m1

Составляем уравнение (5):

m1 · 10 + (200 — m1) · 50 = 200 · 20

40 ·m1 = 6000

m1 = 150 (г),

m2 = 200 — m1 = 200 — 150 = 50 (г)

Ответ: 150 г, 50 г.

Пример 2: Определите массы 25%-ного (по массе) раствора и воды, необходимые для получения 200 г 10%-ного раствора.

Решение:

ω1 = 25%, ω2 = 0%, ω3= 10%, m3 = 200 г

Составляем уравнение (5):

m1 ·25 + m2 · 0 = 200 · 10

25 · m1 = 2000

m1 = 80 (г),

m2 = 200 — m1 = 200 — 80 =120 (г)

Ответ: 80 г, 120 г.

ЗАДАЧИ НА ВЫСУШИВАНИЕ И ВЫПАРИВАНИЕ

При решении этих задач надо иметь ввиду, что все тела, вещества, продукты содержат в себе воду, которая частично испаряется. Поэтому при решении этих задач мы каждый раз разделяем данное нам вещество на воду и «сухой остаток», масса которого не меняется в условиях задачи.

Задача 1. Собрали 8 кг свежих цветков ромашки, влаж­ность которых 85%. После того как цветки высушили, их влажность составила 20%. Чему равна масса цветков ромашки после сушки?

Решение.

Заполним таблицу по условию задачи:

1) 0,15 · 8 = 1,2 кг — масса сухого вещества в 8 кг;

2) 1,2 кг сухого вещества — это 80% массы высушенных цветов, значит, масса высушенных цветов равна 1,2 : 0,8 = 1,5 кг.

Ответ: 1,5 кг.

Задача 2. Из 22 кг свежих грибов получается 2,5 кг сухих грибов, содержащих 12% воды. Каков процент воды в свежих грибах?

Решение.

Заполним таблицу по условию задачи:

1) 2,5 · 0,88 = 2,2 кг — масса сухого вещества;

2) 2,2 : 22 · 100 = 10% сухого вещества содержится в свежих грибах;

3) 100 — 10 = 90% воды в свежих грибах.

Ответ: 90%.

Задача 3. Только что добытый каменный уголь содержит 2% воды, а после двухнедельного пребывания на воздухе он содержит 12% воды. На сколько килограммов увеличится масса одной добытой тонны угля после того, как она две недели пролежит на воздухе?

Эта задача обратна предыдущим, здесь влажность угля увеличива­ется за счет поглощения влаги из воздуха.

Решение.

Заполним таблицу по условию задачи:

1) 1000 · 0,98 = 980 кг — сухого вещество в добытом угле;

2) 980 кг — это 88%, 980 : 0,88 =1114 кг — масса угля после двух недель пребывания на воздухе;

3) 1114 — 1000 = 114 кг — увеличение массы одной добытой тонны угля.

Ответ: на 114 кг.

Задачи, решаемые другими способами.

Задача 10. Трава при высыхании теряет около 28% своей массы. Сколько было накошено травы, если из нее было получено 1,44 т сена?

Решение. Заполним таблицу по условию задачи:

Зависимость прямо пропорциональная. Задача решается простой пропорцией.

Существует множество способов решения задач на смеси и сплавы. Для каждой конкретной задачи подходит свой метод решения, иногда не один. Ученику придется самому решать, какой способ он будет использовать. Однако знание способов решения задач на смеси и сплавы для их решения не достаточно: нужно уметь рассуждать, решать задачи на дроби и проценты, на составление уравнений и их систем.

Как правило, ученики очень не любят задачи на сплавы и смеси. Для них они являются сложными и непонятными.

Поэтому многие даже время не тратят на попытки решения такой задачи в ЕГЭ, а просто пропускают ее. А зря!

Сейчас покажем, как можно решить такую задачу, выполнив всего три действия.

1. Как решить задачу на смеси и сплавы: 3 действия
2. Примеры решения задач на смеси: от простого к сложному
3. Примеры решения задач на сплавы: от простого к сложному

Как решить задачу на смеси и сплавы: 3 действия

 Итак, решение любой задачи на смеси и сплавы сводится к выполнению трех действий:

1. Необходимо составить таблицу, в которой указываем общую массу каждого вещества и чистую массу каждого вещества. Эти данные содержатся в условии задачи. Если какие-то данные в условии отсутствуют, то обозначаем их как неизвестные — х, у.
2. Составляем систему уравнений, основываясь на том, что при соединении двух смесей (или сплавов) их массы складываются. Т.е. мы складываем как общую массу двух изначальных смесей (или сплавов), так и чистую массу каждого вещества, содержащихся в них. Решаем полученную систему уравнений.
3. После решения системы уравнений и нахождения всех неизвестных обязательно возвращаемся к условию задачи и смотрим, что требовалось найти. Многие ученики, решив правильно систему уравнений, неправильно записывают ответ. Ведь решение системы – это еще не ответ к задаче! Вернитесь к условиям задачи, прочитайте, что именно требовалось найти, и запишите ответ.

 Примеры решения задач на смеси: от простого к сложному

 А теперь разберем на примерах, как с помощью этих трех действий решать задачи на смеси и сплавы.

Задача 1

Смешали 3 литра раствора, содержащего 20% кислоты, и 5 литров раствора, содержащего 40% той же кислоты. Какова концентрация кислоты в полученном растворе.

Решение:

Для решения задачи выполняем три действия, о которых мы говорили выше:

1. Составляем таблицу, в которой указываем общую массу раствора и массу чистого вещества, то есть в нашем случае – кислоты.

Из условий задачи имеем три раствора:

Раствор 1: 3 литра с 20% кислотой, т.е. общая масса = 3 литра, масса чистого вещества = 3 * 20% = 3 * 0,2 = 0,6

Раствор 2: 5 литров с 40% кислотой, т.е. общая масса = 5 литров, масса чистого вещества = 5 * 40% = 5 * 0,4 = 2

Раствор 3: какое-то количество раствора (обозначим его общую массу за х) с какой-то концентрацией кислоты (обозначим ее чистую массу за у), заносим эти данные в таблицу:Первое действие выполнено, переходим ко второму.

2. Составляем уравнения. Вспоминаем, что общая масса раствора 3 является суммой общих масс раствора 1 и раствора 2. А масса чистого вещества в растворе 3 является суммой массы чистового вещества в растворе 1 и массы чистового вещества в растворе 2. Таким образом, получаем:

3 + 5 = х

0,6 + 2 = у

Решаем простейшее уравнение и получаем, что х = 8, а у = 2,6. Таким образом, раствор 3 получился 8 литров, из которых 2,6 литра – это кислота.

Но ответ к задаче записывать рано! Переходим к третьему действию решения нашей задачи.

3. Возвращаемся к условию задачи и вспоминаем, а что же требовалось найти. В нашей задаче требовалось определить концентрацию кислоты в растворе 3. Когда мы решили уравнения, мы нашли общую массу раствора 3 и массу чистого вещества (кислоты), содержащегося в нем.

Чтобы определить концентрацию вещества необходимо разделить массу чистого вещества на общую массу раствора.

Таким образом, концентрация кислоты в растворе 3 равна:

2,6 / 8 = 0,325

Переводим долю вещества в проценты. Для этого умножаем полученный результат на 100:

0,325 * 100 = 32,5%

Ответ: 32,5%

Задача 2

Газ в сосуде А содержал 21% кислорода, а газ в сосуде В содержал 5% кислорода. Масса газа в сосуде А была больше массы газа в сосуде В на 300 г. Когда перегородку между сосудами убрали, газы перемешались, и получился третий газ, который содержит 14,6% кислорода. Найти массу третьего газа.

Решение:

1. Составляем таблицу. Для этого обозначим массу газа в сосуде В – х. Остальные данные берем из условий задачи и формируем таблицу:2. Составляем уравнение. Известно, что третий газ имеет содержание кислорода 14,6%, соответственно мы можем приравнять массу чистого вещества газа 3 к 0,146 * (х + (х +300)). Получим уравнение:

(х +300)  * 0,21 + х * 0,05 = 0,146 (х + (х +300))

0,21х + 63 + 0,05х = 0,292х + 43,8

0,26х + 63 = 0,292х + 43,8

0,032х = 19,2

х = 600

3. Возвращаемся к условиям задачи и вспоминаем, что нужно было найти. А найти нам нужно было массу третьего газа. Подставляем в уравнение общей массы газа 3 из таблицы и получаем:

600 + 600 + 300 = 1500 г

Ответ: масса третьего газа равна 1500 г.

Задача 3

Смешали 40%ый и 15%ый растворы кислоты, затем добавили 3 кг чистой воды, в результате чего получили 20%ый раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%ый раствор кислоты. Сколько килограммов 40%го и 15%го растворов кислоты было смешано?

Решение:

1. Составляем таблицу. По условиям задачи мы имеем пять растворов:

Раствор 1: 40%ая кислота. Обозначим ее массу за х, тогда масса чистого вещества = х * 40% = 0,4х

Раствор 2: 15%ая кислота. Обозначим ее массу за у, тогда масса чистого вещества = х * 15% = 0,15х

Вода: вода, масса которой равна 3 кг. Концентрация кислоты в воде равна 0. Таким образом, масса чистого вещества равна 3 * 0 = 0

Раствор 3: 80%ая кислота. Ее масса по условию задачи равна 3 кг, тогда масса чистого вещества равна 3 * 80% = 3 *0,8 = 2,4

Раствор 4: соединение раствора 1, раствора 2 и воды. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 0

Раствор 5: соединение раствора 1, раствора 2 и раствора 3. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 2,4.

Сводим полученные результаты в таблицу:2. Составляем уравнение.

По условиям задачи раствор 5 имеет концентрацию 50%. Таким образом, чтобы получить массу чистого вещества в растворе 5 нужно его общую массу умножить на концентрацию. Получаем (х + у + 3) * 0,5. Теперь берем массу чистого вещества раствора 5, которую мы выразили в таблице и приравниваем два этих уравнения:

 (х + у + 3) * 0,5 = 0,4х + 0,15у + 2,4

Аналогично поступаем с раствором 4. По условиям задачи его концентрация равна 20%. Тогда получаем следующее уравнение:

(х + у + 3) * 0,2 = 0,4х + 0,15у

Объединяем полученные уравнения в систему:Решаем систему и получаем х = 3,4, у = 1,6

3. Возвращаемся к условиям задачи.

По условиям задачи необходимо было найти, какое количество килограммов 40%го и 15%го растворов кислоты было смешано. Общая масса 40%й кислоты мы обозначали х, а общую массу 15%й кислоты мы обозначили у. Следовательно, масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.

Ответ: масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.

Примеры решения задач на сплавы: от простого к сложному

Задача 1

Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы, содержащий 1/12 часть олова, сплавляется с другим куском, содержащим 1/10 часть олова. Полученный сплав содержит 1/11 часть олова. Найдите вес второго куска, если вес первого равен 84 кг

Решение:

1. Составим таблицу. Обозначим массу второго куска – х.2. Составим уравнение. По условию задачи сплав 3 содержит 1/11 часть олова, тогда масса чистого вещества равна  1/11 * (84 + х). Таким образом, можно составить следующее уравнение:

1/12 * 84 + 1/10 * х = 1/11 * (84 + х)

7 + х/10 = 84/11 + х/11

х/10 – х/11 = 7/11

х/110 = 7/11

х/10 = 7

х = 70

3. Возвращаемся к условию задачи. Найти нужно было вес второго куска. Вес второго куска равен 70 кг.

Ответ: 70 кг.

Задача 2

Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Решение.

1. Составим таблицу. Пусть масса первого сплава – х, масса второго сплава – у. Остальные данные берем из решения и составляем таблицу:2. По условиям задачи масса третьего сплава равна 200 г, значит:

х + у = 200

Содержание меди в третьем сплаве по условиям задачи равно 30%, т.е. масса чистого вещества равна 0,3(х + у). Следовательно, берем массу чистого вещества из таблицы и приравниваем:

0,15х + 0,65у = 0,3(х + у)

Получившиеся уравнения сводим в систему и решаем ее:х = 200 – у

0,15(200 – у) + 0,65у = 0,3 * 200

30 – 0,15у + 0,65у = 60

0,5у = 30

у = 60

х = 140

3. Возвращаемся к условиям задачи. Необходимо было найти массу первого и второго сплава. Масса первого сплава — 140 г, масса второго сплава -60 г.

Ответ: 140 г и 60 г.

Задача 3

В первом сплаве  содержание меди составляет 70%, а во втором – 40%. В каком отношении надо взять эти сплавы, чтобы получить из них новый сплав, который содержит 50% меди?

Решение:

1. Составим таблицу. Обозначим массу первого сплава – х, массу второго сплава – у. Тогда:2. По условиям задачи содержание меди в третьем сплаве равно 50%. Таким образом, масса чистого вещества равна 0,5 (х + у). Приравняем полученное уравнение к массе чистого вещества в составе третьего сплава из таблицы, получим:

0,7х + 0,4у = 0,5 (х + у)

0,7х + 0,4у = 0,5х + 0,5у

0,2х = 0,1у

х/у = ½

3. Возвращаемся к условию задачи. Необходимо было определить отношение первого и второго сплавов в третьем сплаве. Отношение сплавов равно ½.

Ответ: ½

Итак, решение задач на сплавы и смеси можно свести к трем действиям: составление таблицы, составление уравнения (или системы уравнений), возвращение к условиям задачи, чтобы дать ответ на поставленный вопрос. Задание 11 ЕГЭ по математике профильного уровня является одной из самых сложных задач, так как может содержать текстовую задачу любого типа. Это может быть как задача на сплавы и смеси, так и задача на движение, работу, проценты. Как решать все эти задачи вы можете узнать на нашем сайте или

Тема: «Способы решения задач на растворы, смеси и сплавы»

Оглавление:

1.Введение……………………………………………………………………………………………..

2. Задачи на растворы, смеси и сплавы…………………………………………..

2.1. Теоретические основы решения задач на растворы, смеси и сплавы ………………………………………………………………………………………

2.2. Способы решения задач на растворы, сплавы и смеси…………….

2.3. Решение задач на растворы, смеси и сплавы…………………………….

3. Заключение………………………………………………………………………………….

4. Список источников информации………………………………………………..

5. Приложение…………………………………………………………………………………

Введение

При подготовке к сдаче ЕГЭ по математике на профильном уровне встретила задачи на растворы, смеси и сплавы, которые в школьном курсе математики почти не рассматриваются.

Они также встречаются на уроках химии и физики.

Имеют практическое значение в повседневной жизни. Например, как правильно приготовить маринад для консервирования, как смешать клей для обоев, приготовить раствор для заливки фундамента дома, разбавить уксусную кислоту для употребления в пищу, приготовить различной концентрации растворы.

Задачи на растворы, смеси и сплавы являются хорошим средством развития логического мышления, средством к углублению свои знаний .

Одним из возможных путей подготовки к ЕГЭ является изучение методов (способов, алгоритмов) решения задач на растворы, смеси и сплавы. В данной ситуации будет полезным не только самому научиться решать такого типа задачи, но и научить одноклассников.

Объект исследования: Задачи на смеси и сплавы

Предмет исследования: Способы решения задачи на растворы, смеси и сплавы

Цель: Изучить способы решения задач на смеси и сплавы.

Задачи: 1. Изучить способы решения задачи на растворы, смеси и сплавы.

2.Выявить алгоритм решения задач данного вида.

3. Научиться решать задачи на растворы, смеси и сплавы. Гипотеза: все задачи на растворы, сплавы и смеси делятся на несколько типов, а каждый из типов имеет конкретный способ решения.

Человеку часто приходится смешивать различные жидкости, порошки, газообразные или твердые вещества, или разбавлять что-либо водой.

В задачах такого типа эти операции приходится проводить мысленно и выполнять расчеты.

Текстовые задачи на смеси, сплавы и растворы входят в различные сборники заданий по подготовке к итоговой аттестации по математике за курс основной школы, включаются в варианты ЕГЭ.

Теоретические основы решения задач на растворы, смеси, сплавы.

Чтобы лучше понимать условия задач, необходимо знать следующие понятия:

• Все получающиеся сплавы или смеси однородны.

• При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.

• Процент — одна сотая любого вещества.  

• Производительность объекта — скорость работы

• Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе.  

• Это отношение может быть выражено либо в дробях, либо в процентах.

• Сумма концентраций всех компонент, составляющих смесь, равна единице.

Глава 2. Типы задач «на смеси сплавы, растворы». Способы их решения.

Все задачи на растворы, смеси, сплавы, можно разделить на три типа:

• на вычисление концентрации;

• на вычисление количества чистого вещества в смеси (или сплаве);

• на вычисление массы смеси (сплава).

Существуют следующие способы решения задач:

• с помощью таблиц;

• с помощью схемы;

• старинным арифметическим способом;

• алгебраическим способом;

• с помощью графика;

• с помощью расчетной формулы.

• правило квадрата

• приравнивание площадей равновеликих прямоугольников

• Способ Л.Ф.Магницкого для трех веществ

• Правило креста

Алгоритм решения задачи на сплавы, растворы и смеси:

• Изучить условия задачи;

• Выбрать неизвестную величину (обозначить ее буквой);

• определить все взаимосвязи между данными величинами;

• Составить математическую модель задачи (выбрать способ решения задачи, составить пропорцию или уравнение относительно неизвестной величины) и решить ее;

• провести анализ результата.

Глава 3. Рассмотрим несколько задач и решим их различными способами.

Задача 1. Сколько нужно добавить воды в сосуд, содержащий 200 г
70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?

Решение: 1 способ – с помощью таблицы:

Наименование веществ, смесей

Наименование веществ, смесей

Масса

раствора (г)

Масса вещества (г)

Исходный раствор

70 % = 0,7

200

0,7·200

Воды долили

—

x

—

Новый раствор

8 % = 0,08

200 + x

0,08(200 + x)

Так как подливали только воду, масса уксусной кислоты в растворе не изменилась. Составляем уравнение : 0,08(200 + х) = 0,7·200

16 + 0,08х = 140

0,08х = 124

х = 1550г

Ответ :1,55 кг воды.

Уксусная кислота

Уксусная кислота

70%

8%

+ х литров воды

200 (200 + х) г.

0,08(200 + х) = 0,7·200; 16 + 0,08х = 140; 0,08х = 124; х = 1550г Ответ :1,55 кг воды.

Задача 2: В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Решение — с помощью формулы:

Концентрация раствора равна

 Объем вещества в исходном растворе равен 0,12*5=0,6 литра. При добавлении 7 литров воды общий объем раствора увеличится, а объем растворенного вещества останется прежним. Таким образом, концентрация полученного раствора равна: 

Ответ: 5.

Задача 3: Сначала приготовили 25%-ый водный раствор поваренной соли. Затем одну треть воды выпарили. Найдите концентрацию получившегося раствора.

Решение – с помощью схемы:

До выпаривания:

После выпаривания:

Сейчас соль стала составлять третью часть всего раствора, т.е. 100% : 3 = %

Ответ: %.

Задача 4: Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение: 1 способ – с помощью формулы.

Пусть количество каждого из растворов было V. Тогда количество сухого вещества в первом растворе 0,15V , а во втором – 0,19V. После того как растворы смешали их общий объем стал 2V, а количество сухого вещества в смеси стало 0,15V+0,19V. Концентрация раствора равна:

Таким образом, концентрация полученного

раствора равна:

Ответ: 17.

2 способ — правило креста или прямоугольника

15

19-х

х

19

Х-15

Запишем исходные концентрации в левый столбец таблицы, искомую полученную концентрацию х запишем в центральный столбец. Правый столбец таблицы заполним разностями исходных и полученной концентрации, вычитая из

большей концентрации меньшую.

Отношение полученных разностей

равно отношению долей, в которых требуется смешать растворы для получения из растворов исходной концентрации раствора с требуемой концентрацией. Так как объемы смешиваемых растворов равны, имеем:

Ответ: 17.

Задача 5. Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Решение — с помощью схемы:

Задача 6 Свежие абрикосы содержат 80 % воды по массе, а курага (сухие абрикосы) – 12 % воды. Сколько понадобится килограммов свежих абрикосов, чтобы получить 10 кг кураги?

Решение: (с помощью схемы)

При высыхании абрикосов испаряется вода, количество сухого вещества не изменяется. Выразим количество сухого вещества в свежих абрикосах и в кураге. Пусть взяли х кг свежих абрикосов. Тогда схема для решения такой задачи имеет вид: вода

вода

с.в.

с.в.

20%

88%

х кг *0,2

10 кг *0,88

80%

12%

=

Составим уравнение, подсчитав количество сухого вещества в левой и правой части схемы:

0,2х=8,8

х=44.

Ответ:44кг.

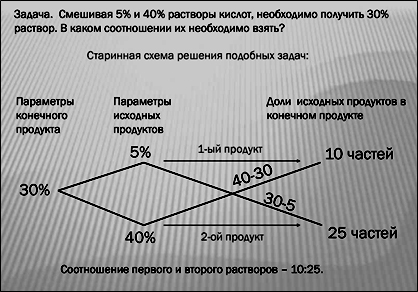
Задача 7. При смешивании 5% -ного раствора кислоты с 40% -ным раствором кислоты получили 140 г 30% -ного раствора. Сколько грамм каждого раствора надо было взять?

5

10

30

40

25

Решение — старинным арифметическим способом.

Рассмотрим пары 30 и 5; 30 и 40. В каждой паре их большего числа вычтем меньшее и результат запишем в конце соответствующей чёрточки. Получилась схема:

Из неё делается заключение, что 5% раствора следует

взять 10 частей, а 40 % — 25 частей. Узнав, сколько

приходится на одну часть 140: (10+25) = 4 г., получаем,

что 5% — ного раствора необходимо взять 40г,

а 40% -ного -100 г

Ответ: 40 г — 5% -ного раствора и 100г — 40% — ного раствора.

Задача 8 : В 100г 20%-ного раствора соли добавили 300г её 10%-ного раствора. Определите процентную концентрацию раствора

с помощью расчетной формулы

m₁=100г .

m₂=300г . а= а= =0,125

а₁=0,2 .

а₂=0,1 .

………….

а -? Ответ:12,5%

с помощью правила креста

0,2 Х- 0,1

Х

0,1 0,2- Х

1:3=(х-0,1):(0,2-х);

Х=0,125; х=12,5%.

Ответ: х=12,5%.

х + у = 1 { х + у = {

х + у = 1

х + у =