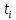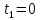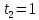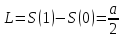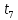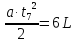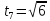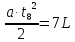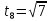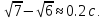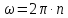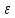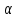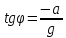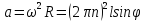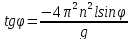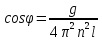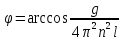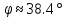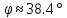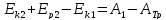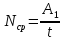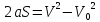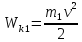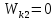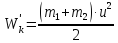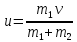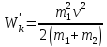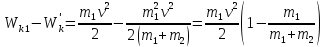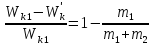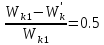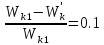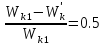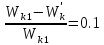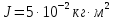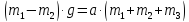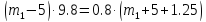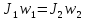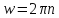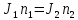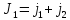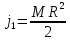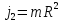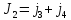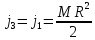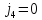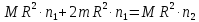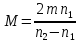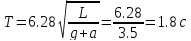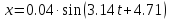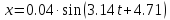Как найти массу платформы физика

40

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

РГЗ1 по физике, вариант 2

1.13 Наблюдатель стоит в начале
электропоезда. Первый вагон прошел мимо
него за время
.
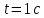
Какое время будет двигаться мимо него
седьмой вагон? Движение поезда
равноускоренное, его начальная скорость
.

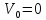
Решение:

Скорость поезда при заданных условиях
будет описываться формулой:

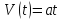
Пройденное расстояние:

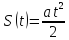
Будем обозначать через

момент времени, когда начало
-го
вагона поравнялось с наблюдателем.
Например,

,

.

По условию,

, где

– длина вагона.

Значит,

.

Начало седьмого вагона поравняется с
наблюдателем в момент

, к этому времени проедут шесть вагонов,
поэтому

,

.

Конец седьмого вагона — это начало
восьмого:

,

.

Ответ:

1.29 Колесо автомашины вращается
равноускоренно. После 50 полных оборотов
частота вращения колеса возросла от n₁
= 4 об/с до n₂ = 6
об/с. Определить угловое ускорение
колеса
.

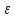
Решение:

,

,

,

.

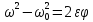
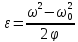
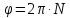
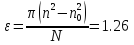
Ответ:

= 1.26 рад/с².

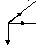
2.28 Грузик, привязанный к шнуру
длиной l = 1.5 м, вращается в горизонтальной
плоскости с частотой n = 28 об/мин. Какой
угол

с вертикалью образует шнур?

Решение:

n = 28 об/мин = 0.46 Гц

OX:
,

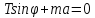
OY:
,

,

,

,

,

,

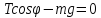
Ответ:

3.13 Автомобиль массой m = 4 т подъезжает
к горке высотой h = 10 м и длиной склона S
= 80 м со скоростью V₀=36 км/ч. Какую
среднюю мощность развивает автомобиль
на подъеме, если его скорость на вершине
горы при постоянной силе тяги оказалась
V = 21,6 км/ч? Коэффициент трения принять
равным
.

Решение:

Автомобиль в начале горки имел кинетическую
энергию Е_к1, к конце горки имел
Е_к1+Е_p2.
При этом двигатель совершил работу А₁
и сила трения совершила работу А_тр.
Изменение энергии тела равно работе
сил, приложенных к телу:

Из этого уравнения находим А₁

,
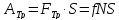
делаем рисунок, указываем силы,
действующие на машину, видим как найти
силу реакции опоры. Найдем энергию.

, время t ищется из
,
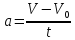
а ускорение ищется из

.

Ответ:

3.39 Движущееся тело массой m₁
ударяется о неподвижное тело массой
m₂. Считая удар неупругим и
центральным, найти, какая часть
первоначальной кинетической энергии
переходит при ударе в теплоту. Задачу
решить сначала в общем виде, а затем
рассмотреть следующие случаи: 1) m₁
= m₂; 2) m₁ = 9m₂.

Решение:

Кинетическая энергия первого тела до
удара

; кинетическая энергия второго тела до
удара

. После удара кинетические энергии обоих
тел

, где

— общая скорость тел.

Следовательно,

. Тогда кинетическая энергия, перешедшая
при ударе в тепло:

. Искомое отношение:

.

1. Если m₁ =
   m₂ , то
   

2. Если m₁ =
   9m₂ , то
   

Ответ: при m₁
= m₂
,

, при m₁ =
9m₂ ,

.

4.13 Через блок перекинута невесомая
нить, к концам которой привязаны два
груза. Груз массой m₂
= 5 кг поднимается со скоростью, меняющейся
по закону V = 5 + 0,8t
(м/с), груз массой m₁
опускается. Момент инерции блока

, его радиус R = 0,2 м.
Найти массу опускающегося груза m₁.
Трением пренебречь.

Решение:

Ускорение грузов будет а = 0,8 м/с²
(из данного закона движения).

Заменим блок материальной точкой массы
m₃, обращающейся по
окружности радиусом R
(это будет «инерционная» масса
блока).

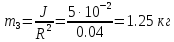
Составим простое уравнение сил (m₁
больше m₂)

.

Подставим в него все известные значения:

.

Осталось одно неизвестное m₁.

Ответ:

4.38 Платформа в виде диска вращается
по инерции около вертикальной оси с
частотой n₁ = 14 об/мин. На краю
платформы стоит человек. Когда человек
перешел в центр платформы, частота
вращения возросла до n₂ = 25 об/мин.
Масса человека m = 70 кг. Определить массу
платформы M. Момент инерции
человека рассчитывать так же, как и для
материальной точки.

Решение:

Закон сохранения момента импульса

, или учитывая что

,

. Момент инерции

, где

— момент инерции диска,

— момент инерции человека, момент инерции

, где

, а

, т.к. расстояние между осью и человеком
стало равно 0. Итак

отсюда

.

Ответ:

5.3 Математический маятник установлен
в лифте, который поднимается с ускорением
а = 2,5 м/с². Определить период Т
собственных колебаний маятника. Его
длина равна 1 м.

Решение:

.

Ответ: T = 1.8 c.

5.28 Даны амплитуда и период свободных
колебаний пружинного маятника: А = 4 см,
Т = 2 с. Написать уравнение этих колебаний.
В момент возникновения колебаний х(0) =
0, х(0) < 0.

Решение:

x < 0 — пружина сжата на
амплитуду 4 см , Фаза Q =
4,71, то есть сдвинута на 270ᵒ, угловая
скорость

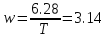
Уравнение гармонических колебаний

Подставив данные в формулу получим:

Ответ:

Соседние файлы в папке Физика

• #
• #

• Комментировать
• Жалоба
• Ссылка