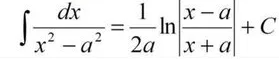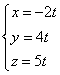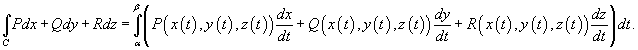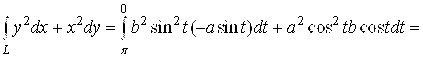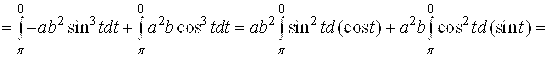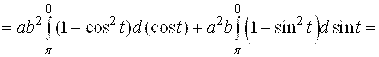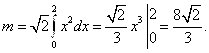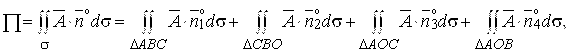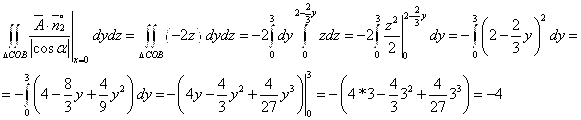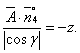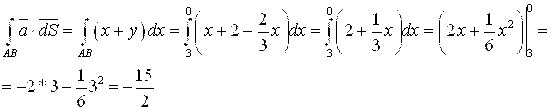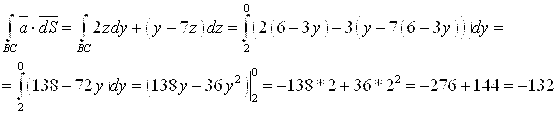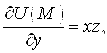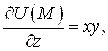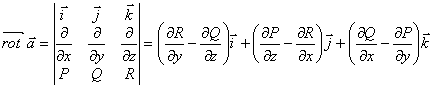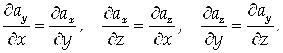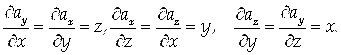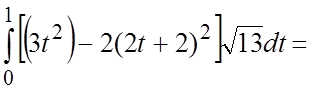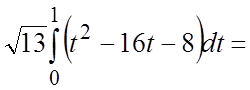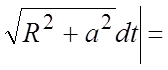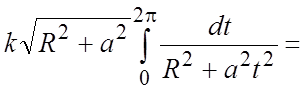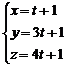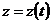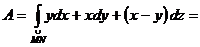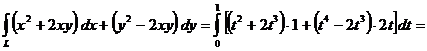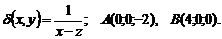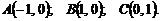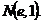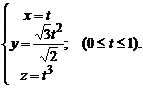Вариант 13
Вычислить криволинейные интегралы:
1. , где
— отрезок прямой ОВ; О(0;0;0); В(-2;4;5)
Решение
Сначала составим уравнение прямой OB.
Введем параметр T: и перепишем уравнение прямой в параметрической форме:
Далее применяем формулу
Очевидно, что параметр T изменяется в интервале [0,1]. Тогда криволинейный интеграл равен
Ответ:
2. 
— дуга кривой
,
Решение
Так как кривая L задана в полярной системе координат, то для вычисления криволинейного интеграла следует использовать формулу
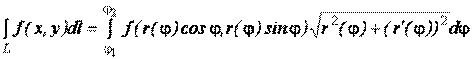
В силу того, что
,
Имеем
Ответ:
3. , где
— окружность
.
Решение
Перейдем к полярным координатам:
Уравнение кривой
примет вид
Для вычисления интеграла применим формулу 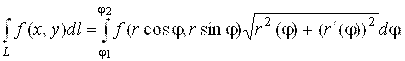
Так как
то
Ответ:
4. , где
— верхняя половина эллипса
., «пробегаемая» по ходу часовой стрелки.
Решение
По формуле
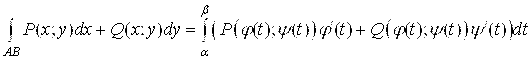
Имеем
,
,
,
,
,
,
,
.
Тогда

Ответ:
5. Показать, что данное выражение является полным дифференциалом функции . Найти функцию
.
.
Решение
P(X;Y)= , Q(X;Y)=,
= ,
=
=
.
Так как P, Q, ,
непрерывны и
=
, то данное выражение является полным дифференциалом некоторой функции F(X;Y) и
В качестве (X0;Y0) можно брать любую точку из области непрерывности функций P, Q, ,
, поэтому возьмем (0;0).
Ответ:
6. Вычислить массу отрезка прямой , заключённого между координатными осями, если линейная плотность в каждой его точке пропорциональна квадрату абсциссы в этой точке, а в точке
равна 4.
Решение
Так как линейная плотность в каждой точке пропорциональна квадрату абсциссы в этой точке, а в точке равна 4, то
По формуле для массы Для вычисления интеграла воспользуемся формулой
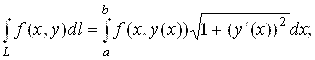
Так как то
Ответ:
1. Дана функция и точки
,
. Вычислить: 1) производную этой функции в точке
по направлению
; 2)
Решение
Найдём направляющие косинусы вектора . Его длина
. Следовательно
,
,
Вычисляем частные производные функции в точке
,
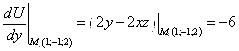
Тогда по формуле
Градиент скалярного поля U есть вектор GradU, направленный по нормали к поверхности уровня поля в сторону возрастания поля и численно равный наибольшей производной по направлению
Он вычисляется по формуле .
В нашем случае ,
,
Тогда ,
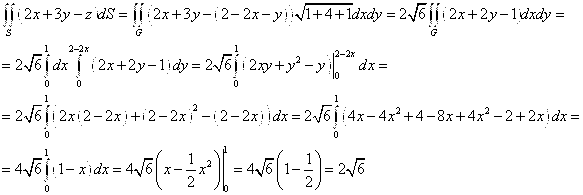
2. Вычислить поверхностный интеграл первого рода по поверхности S, где S – часть плоскости , отсеченная координатными плоскостями.
Решение
Данная поверхность S представляет собой часть плоскости , расположенную в первом октанте.
Запишем уравнение плоскости в виде . Тогда
,
.
Используя формулу , имеем
Ответ:
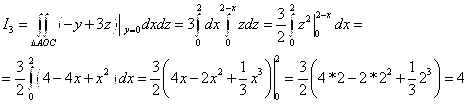
3. Вычислить поверхностный интеграл второго рода , где S – часть поверхности параболоида
(нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостью z=2.
Решение
Поверхность S является частью параболоида , отсеченной плоскостью
. Поверхность S однозначно проецируется на плоскость
в область
― круг радиуса
с центром в начале координат. Уравнение окружности
, которая является границей
.
Поэтому, получаем
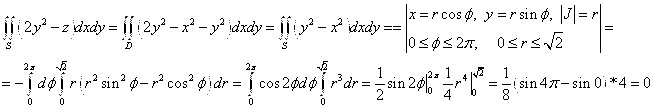
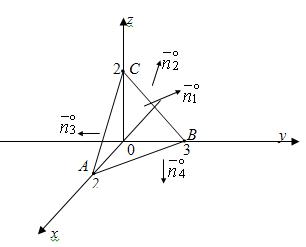
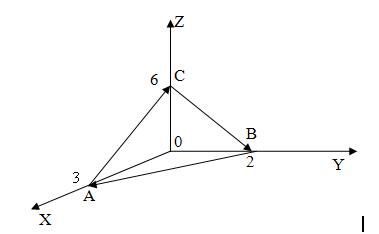
4. Вычислить поток векторного поля через внешнюю сторону пирамиды, образуемою плоскостью
и координатными плоскостями, двумя способами: а) использовав определение потока; б) с помощью формулы Остроградского-Гаусса.
,
:
Решение
При вычислении потока данного примера рассмотрим сумму потоков, т. к. поверхность состоит из четырех частей.
Где – соответственно нормали к поверхностям
и
.
Будем вычислять каждый из слагаемых интегралов отдельно. В первом интеграле взаимно однозначно проектируется, например, на плоскость
, а уравнение его плоскости
.
Принимая ,
Найдем единичный вектор нормали к этой плоскости .
Здесь , что и соответствует нормали к внешней стороне треугольника. После этого находим

Во втором интервале ,
и

В третьем интеграле и

В четвертом интеграле и
Окончательно получаем .
Решим задачу с помощью теоремы Остроградского:
Поэтому
Где – объем пирамиды
.
Ответ:
5. Вычислить циркуляцию векторного поля по контуру треугольника, полученного в результате пересечения плоскости
:
с координатными плоскостями, при положительном направлении обхода относительно нормального вектора
этой плоскости двумя способами: 1) использовав определение циркуляции; 2) с помощью формулы Стокса
,
:
Решение
В результате пересечения плоскости с координатными плоскостями получим треугольник
и укажем на нем положительное направление обхода контура
.
1. Вычислим циркуляцию данного поля по формуле:
На отрезке имеем:
,
,
,
.
,
,
,
На отрезке ,
,
,
,
,
,
,
На отрезке ,
,
,
,

2. Вычислим циркуляцию данного поля с помощью формулы Стокса. Для этого вычислим:

в формуле Стокса возьмем боковую поверхность пирамиды
:
.
По формуле Стокса имеем: ,
Где ,
Следовательно, .
Ответ:
6. Найти величину и направление наибольшего изменения функции в точке
.
Решение
Находим частные производные функции в любой точке
и в точке
:
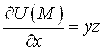
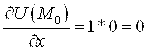
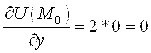

Тогда в точке имеем
. Наибольшая скорость изменения поля в точке
достигается в направлении
:
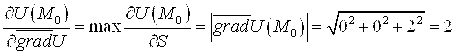
7. Найти наибольшую плотность циркуляции векторного поля в точке
.
Решение
Модуль ротора векторного поля равен максимальному значению поверхностной плотности циркуляции векторного поля. По формуле:
Тогда
Тогда в т. ,
Ответ:
8. Выяснить, является ли векторное поле потенциальным.
Решение
Поле является потенциальным, если выполнены следующие условия:
В нашем случае
Следовательно, поле потенциальное.
| < Предыдущая | Следующая > |
|---|
Следствия.
а) Если плоская кривая l задана явно: , и
, то
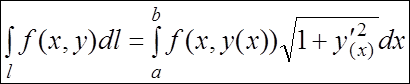
б) Если плоская кривая l задана в полярных
координатах: , то
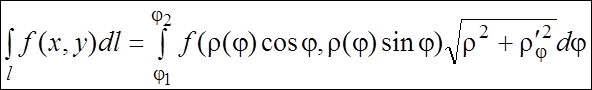
Некоторые приложения КИ-1
1. Масса материальной линии. Пусть ,
—
линейная плотность массы материальной линии l. Тогда масса этой линии
есть:
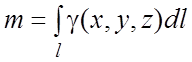
(5.4)
2. Длина пространственной (или плоской) кривой l есть L: 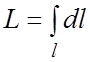
3. Статические моменты и
координаты центра тяжести.
а) Для плоской
линии c плотностью
и
массой m статические моменты относительно координатных осей Oy и Ox:
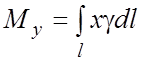
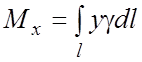
координаты центра тяжести:
,
.
б) Для пространственной
линии l c плотностью и массой m статические моменты
относительно плоскостей и Oxy:
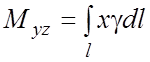
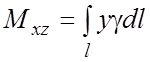
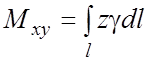
координаты центра тяжести:
,
,
.
Пример 17.
Вычислить
КИ-1: 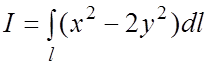
соединяющий точки и
.
Ñ Уравнения отрезка прямой
AB в параметрической форме:
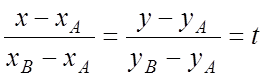
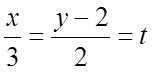
. Тогда
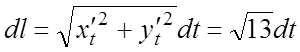
(5.1) имеем 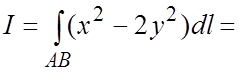
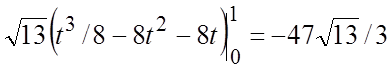
Замечание. В случае явного задания
отрезка прямой
следует воспользоваться
формулой (5.2). #
Пример 18. Вычислить КИ-1: 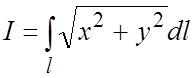
уравнением при условии
.
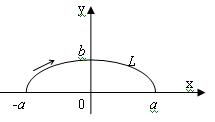
Ñ Для построения кривой l преобразуем уравнение ее
к виду ; таким образом, l есть полуокружность с
центром в точке радиуса 1, расположенная слева
от оси Oy (рис. 14.22).

в подынтегральной функции и в уравнении l наводит на мысль провести вычисления
в полярных координатах, которые связаны с декартовыми координатами формулами . Тогда: из
Рис. 14.22 получаем
– уравнение l в полярных координатах; из рис. 14.22 (или условий
,
,
следует:
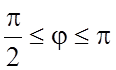
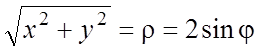
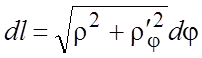
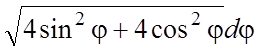
, и из (5.3)
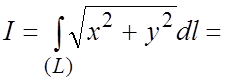
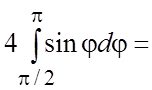
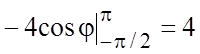
Пример 19. Найти массу одного витка
материальной винтовой линии ,
,
(рис.
14.23), если линейная плотность в точке обратно пропорциональна квадрату расстояния этой точки от начала координат.
Ñ По условию задачи
плотность +
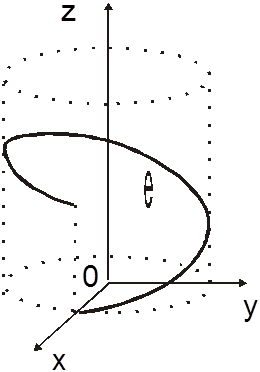
=
, где k – коэффициент про-
порциональности,
. Для одного витка
.
Из формул (5.4) и (5.1) имеем: 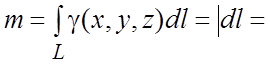
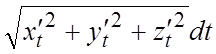
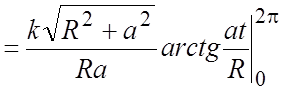
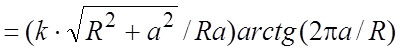
#
Задачи для
самостоятельного решения
Вычислить криволинейные интегралы первого рода:
81. 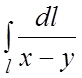
, заключенный между точками
и
.
82. 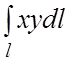
где l – контур прямоугольника с вершинами:
.
83. 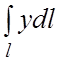
где l– дуга параболы ,
отсеченная параболой .
84. 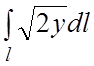
где l– первая арка циклоиды .
85. 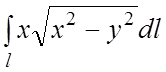
.
86. 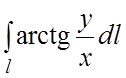
, заключенная внутри круга радиуса R с центром в точке
.
87. 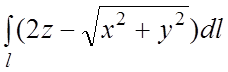
конической винтовой линии ,
,
.
88. 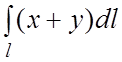
, лежащая в первом октанте.
89. 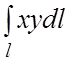
,
.
90. 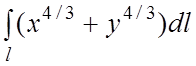
в первом квадранте.
91. Найти массу первого
витка винтовой линии , плотность которой в каждой
точке равна полярному радиусу этой точки.
92. Найти массу линии ,
, от
точки, соответствующей t=0, до произвольной точки, если плотность в
каждой точке обратно пропорциональна квадрату полярного радиуса и в точке равна единице.
93. Найти массу дуги
параболы , если линейная плотность в текущей точке
равна .
Вычислить координаты
центра тяжести дуги однородной кривой :
94. , от точки
до точки
.
95. .
96. .
14.5.2 Криволинейные интегралы второго рода
(КИ-2)
Пусть : 1) в
точках непрерывной кривой AB из пространства определены
ограниченные скалярные функции ;
2) — произвольное разбиение кривой AB на элементарные дуги
с длинами
и
проекциями ,
,
на соответствующие оси координат; 3)
— произвольный набор точек;
4) 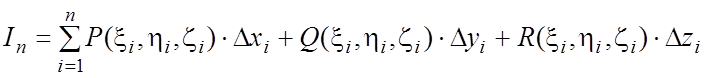
данному разбиению и данному выбору точек.
Определение. Конечный предел
интегральной суммы при
, не зависящий ни от способа разбиения AB , ни от выбора точек
, называется криволинейным интегралом
второго рода от функций по пути AB:
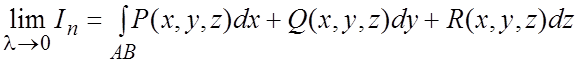
Механически КИ-2
представляет собой работу переменной силы , точка
приложения которой описывает кривую AB.
Пример 4.
Вычислить работу векторного поля 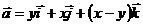
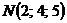
Решение.
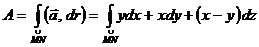
Уравнение прямой 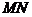
и вычислим производные от функций 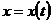
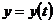
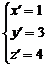
Пределы интегрирования для переменной 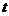
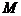
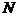
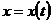
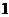
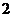
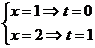
Следовательно,
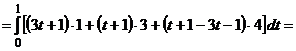
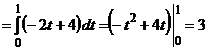
Пример 5.
Вычислите работу векторного поля 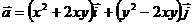
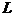
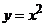
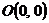
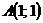
Решение
Зададим кривую 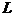
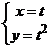
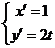
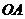

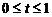
Учитывая это, криволинейный интеграл можно свести к определенному интегралу.
Вариант 1
1. Вычислить момент инерции относительно оси OX однородного участка линии 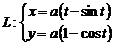
2. Найти работу поля вектора 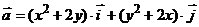
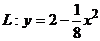
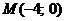
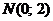
Вариант 2
1. Вычислить массу отрезка прямой AB, если линейная плотность в каждой точке
2. Найти работу поля вектора 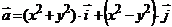
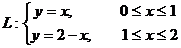
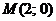
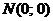
Вариант 3
1. Вычислить массу дуги параболы 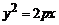
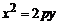
2. Найти работу поля вектора 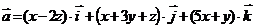
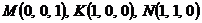
Вариант 4
1. Вычислить массу контура прямоугольника ABCD, если линейная плотность в каждой его точке определяется выражением 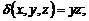
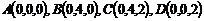
2. Найти работу поля вектора 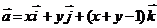
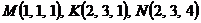
Вариант 5
1. Вычислить длину дуги кривой 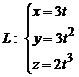
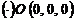
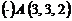
2. Найти работу поля вектора 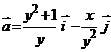
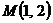
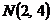
Вариант 6
1. Вычислить массу участка линии 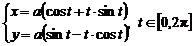
2. Найти работу поля вектора 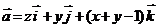
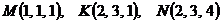
Вариант 7
1. Вычислить момент инерции относительно начала координат однородного первого витка винтовой линии 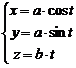
2. Найти работу поля вектора 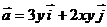
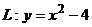
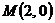
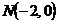
Вариант 8
1. Вычислить массу части окружности 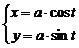
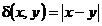
2. Найти работу поля вектора 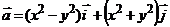
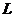
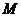
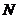
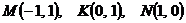
Вариант 9
1. Вычислить статический момент относительно оси OX однородного контура 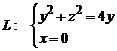
2. Найти работу поля вектора 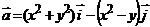
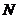
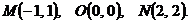
Вариант 10
1. Вычислить массу контура треугольника ABC, если линейная плотность в каждой его точке 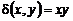
2. Найти работу поля вектора 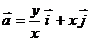
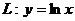
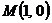
Вариант 11
1. Вычислить момент инерции относительно оси OY однородного участка линии 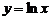
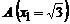
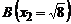
2. Найти работу поля вектора 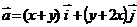
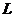
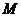
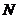
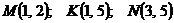
Вариант 12
1. Вычислить массу контура 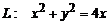
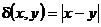
2. Найти работу поля вектора 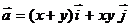
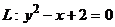
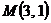
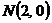
Вариант 13
1. Вычислить статический момент относительно оси OX однородной части кривой 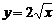
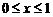
2. Найти работу поля вектора 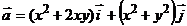
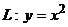
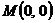
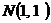
Вариант 14
1. Вычислить массу дуги линии 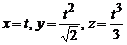
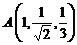
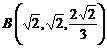
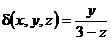
2. Найти работу поля вектора 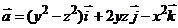
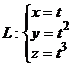
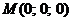
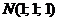
Вариант 15
1. Найти массу контура правого лепестка лемнискаты 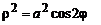
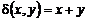
2. Найти работу поля вектора 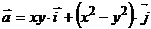
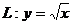
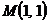
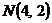
Вариант 16
1. Вычислить длину дуги кривой
2. Найти работу поля вектора 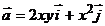
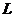
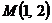
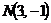
Вариант 17
1. Вычислить массу прямолинейного стержня 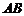
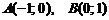
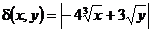
2. Найти работу поля вектора 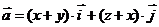
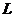
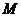
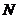
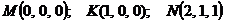
Вариант 18
1. Вычислить момент инерции верхней половины окружности 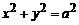
2. Найти работу поля вектора 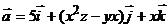
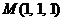
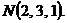
Вариант 19
1. Вычислить массу первого витка винтовой линии 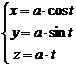
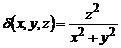
2. Найти работу поля вектора 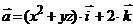
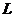
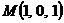
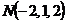
Вариант 20
1. Найти центр тяжести однородной дуги окружности радиуса 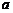
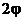
2. Найти работу поля вектора 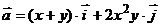
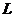
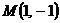
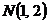
Вариант 21
1. Вычислить массу прямолинейного стержня 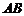
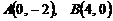
2. Найти работу поля вектора 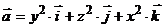
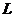
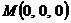
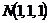
Вариант 22
1. Вычислить длину дуги линии 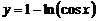
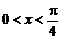
2. Найти работу поля вектора 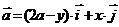
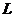
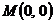
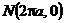
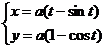
Вариант 23.
1. Вычислить массу контура треугольника 
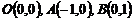
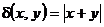
2. Найти работу поля вектора 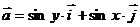
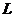
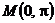
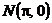
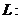
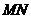
Вариант 24
1. Вычислить момент инерции относительно начала координат участка однородной линии 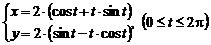
2. Найти работу поля вектора 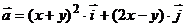
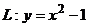
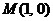
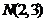
Вариант 25
1. Вычислить массу контура 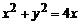
2. Найти работу поля вектора 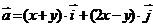
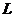
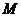
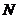
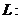
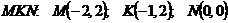
Вариант 26
1. Вычислить длину дуги цепной линии 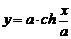
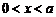
2. Найти работу поля вектора 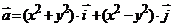
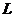
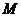
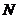
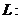
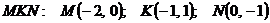
Вариант 27
1. Найти координаты центра тяжести однородной кардиоиды 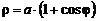
2. Найти работу поля вектора 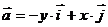
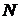
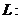
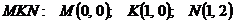
Вариант 28
1. Найти координаты центра тяжести однородной кардиоиды 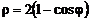
2.
Вариант 29
1. Найти массу четверти эллипса 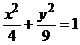
2.
Вариант 30
1. Найти координаты центра тяжести первого витка однородной винтовой линии 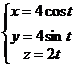
2.
Приложения криволинейных интегралов
Краткая теория
Длина дуги
Длину дуги
плоской или пространственной линии
определяют по формуле:
Масса дуги
Если
– линейная плотность вещества в точках дуги,
то массу
дуги
определяют по формуле:
Статистические моменты
Статистические
моменты
и
плоской дуги
относительно координатных осей
и
определяют по формулам:
Моменты инерции
Моменты
инерции
,
плоской дуги
относительно координатных осей
и
определяют по формулам:
Полярный момент инерции
Полярный
момент инерции
плоской дуги
относительно начала координат определяют по
формуле:
Площадь фигуры
Площадь
фигуры, расположенной в плоскости
и ограниченной замкнутой линией
, вычисляют по формуле:
Работа, приложенная к точке, при перемещении по дуге
Работу, совершаемую силой
приложенной в точке
при перемещении ее по дуге
, вычисляют по формуле:
Примеры решения задач
Задача 1
Найти
момент инерции относительно оси
четверти однородной окружности
, расположенной в первом
квадранте.
Решение
Окружность
однородна, следовательно
, следовательно искомый
момент инерции:
Для
удобства вычислений перейдем к параметрическим уравнениям окружности
Тогда:
Ответ:
Задача 2
Найти
массу дуги кривой
от точки
до
, если плотность в каждой точке
ее равна абсциссе точки;
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
дуги:
Искомая масса будет выражаться
криволинейным интегралом 1-го рода:
Производная:
Искомая масса:
Ответ:
.
Задача 3
Найти
массу дуги окружности
, лежащей в первой
четверти, если плотность в каждой ее точке равна абсциссе точки.
Решение
Плотность:
Искомая масса будет
выражаться криволинейным интегралом 1-го рода:
Параметрическое
уравнение окружности:
Окружность лежит в
первой четверти, поэтому
Ответ:
.
Задача 4
Вычислить
работу силы
при обходе точки ее приложения по границе
области
в положительном направлении, начиная от точки
.
Решение
Искомая
работа будет равна криволинейному интегралу 2-го рода:
Для
вычисления интеграла воспользуемся формулой Грина:
Ответ:
.
Задача 5
Вычислить
работу силового поля
при перемещении материальной точки вдоль пути
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Параметр
:
Перейдем к
определенному интегралу:
Искомая работа:
Ответ:
Задача 6
Вычислить
работу силы
при перемещении материальной точки вдоль линии
от точки
до точки
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ:
Условие
Вычислить массу прямолинейного стержня АВ , где А(0‚-2)‚ В(4‚0)‚ если плотность в каждой его точке обратно пропорциональна расстоянию до начала координат.|

математика
523
Решение
★
m= ∫_ ( ∪ AB) μ (x;y)d [i]l[/i]- криволинейный интеграл первого рода по длине дуги
μ (x;y) — обратно пропорциональна расстоянию произвольной точки М(x;y) до начала координат.
[m]d=sqrt{x^2+y^2} [/m]- расстояние произвольной точки М(x;y) до начала координат.
[m]μ (x;y)=frac{1}{sqrt{x^2+y^2}}[/m]
[b]Составим уравнение прямой АВ:[/b]
[m]frac{x-x_{A}}{x_{B}-x_{A}}=frac{y-y_{A}}{y_{B}-y_{A}}[/m]
[m]frac{x-0}{4-0}=frac{y-(-2)}{0-(-2)}[/m]
[m]frac{x}{4}=frac{y+2}{2}[/m] ⇒ [m]frac{x}{2}=y+2[/m] ⇒ [m]y=frac{1}{2}x-2[/m]
0 ≤ x ≤ 4
тогда
[m]y`=frac{1}{2}[/m]
и
[m]dl=sqrt{1+(y`(x))^2}dx=sqrt{1+(frac{1}{2})^2}dx=frac{sqrt{5}}{2}[/m]
[m]μ (x;y)=frac{1}{sqrt{x^2+y^2}}=frac{1}{sqrt{x^2+(frac{1}{2}x-2)^2}}=frac{1}{frac{5}{4}x^2-2x+4}[/m]
m= ∫_ ( ∪ AB) μ (x;y)d [i]l[/i]= [m]∫ _{0}^{4}frac{1}{frac{5}{4}x^2-2x+4}cdot frac{sqrt{5}}{2}dx[/m] — определенный интеграл=
= [m] sqrt{5}∫ _{0}^{4}frac{1}{5x^2-8x+16}dx=∫ _{0}^{4}frac{1}{x^2-frac{8}{5}x+frac{16}{5}}dx=∫ _{0}^{4}frac{1}{(x-frac{4}{5})^2-(frac{4}{5})^2+frac{16}{5}}dx=∫ _{0}^{4}frac{1}{(x-frac{4}{5})^2-(frac{8}{5})^2}dx[/m]
табличный интеграл см. скрин