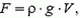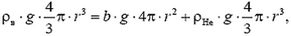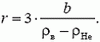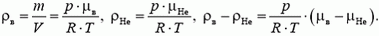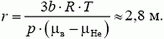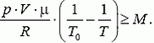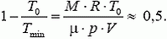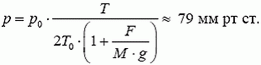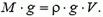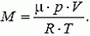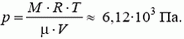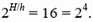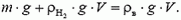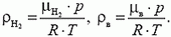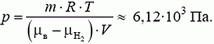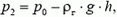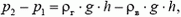Калькулятор Подъемная сила воздушного шара рассчитывает параметры воздушного шара, где в качестве подъемного газа используется горячий воздух. В случае в гелием расчет становится проще. Опять же, если речь идет о задачах на молекулярно-кинетическую теорию, то просят найти либо массу гелия, требуемую для подъема шара с заданной массой оболочки и массой груза, либо массу груза, которую может поднять заданная масса гелия при заданной массе оболочки воздушного шара. Калькулятор ниже позволяет найти любое неизвестное значение, включая массу оболочки. Стоит заметить, что в задачах обычно приводится температура окружающего воздуха и его давление, но для расчета они на самом деле не нужны.
Как обычно, теория и формулы расчета приведены под калькулятором.
Подъемная сила воздушного шара, наполненного гелием
Использовать округленное значение молярной массы воздуха (29)
Точность вычисления
Знаков после запятой: 3
Расчет параметров воздушного шара, наполненного гелием
Воздушный шар поднимается под действием выталкивающей силы, или силы Архимеда, потому что закон Архимеда распространяется не только на жидкости, но и на газы. Соответственно, чтобы шар начал подниматься, выталкивающая сила, действующая на шар, должна превышать силу тяжести. Для решения задач обычно находят граничное условие (по массе), что позволяет приравнять силу тяжести и выталкивающую силу. То есть чуть больше масса гелия, или чуть меньше масса груза — и шар начинает подниматься. Уравнение равновесия выглядит таким образом:
,
где
M — масса оболочки,
m — масса груза,
mₐ — масса гелия в шаре,
mₑ — масса окружающего воздуха, вытесненного шаром,
g — ускорение свободного падения.
Сократив g и перенеся массу нагретого воздуха в правую часть, получим
Разберемся с массой воздуха, вытесненного шаром. Ключевой момент для шаров с гелием — его давление и температура равны давлению и температуре окружающего воздуха. Поэтому, если рассмотреть два одинаковых объема, равных объему, занимаемому гелием, то из уравнения Менделеева-Клапейрона можно записать:
Откуда, после сокращения RT
Молярная масса гелия 4 г/моль, молярная масса воздуха 28.98 г/моль (в задачах часто округляют до 29). Чтобы равенство выполнялось, масса гелия должна быть меньше массы вытесненного воздуха. Получаем следующее выражение для массы воздуха:
Подставив mₑ в равенство выше, получим итоговую формулу, которая связывает все параметры воздушного шара:
Из этого равенства можно получить формулы для вычисления нужного неизвестного.
Масса оболочки:
Масса груза:
Масса гелия:
Стоит заметить, что шары, наполненные гелием, используют для подъема в стратосферу. Давление воздуха там ниже, следовательно, чтобы вытеснить нужную массу воздуха, необходимую для подъема, нужно занять больше объема. Таким образом, шары, предназначенные для подъема в стратосферу, должны иметь возможность сильно расширяться, то есть их оболочка не должна оказывать сопротивления изменению объема шара (об этом, кстати, пишут и в условиях задач). Самый простой способ этого достичь — сделать оболочку «с запасом», поэтому такие воздушные шары при запуске кажутся почти пустыми.
Баканина Л.П. Задачи о воздушных шарах // Квант. — 1975. — № 1. — С. 60-63.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В наш век самолетов и ракет, для которых доступны любые высоты над поверхностью Земли, воздушные шары, громоздкие, ненадежные и неуправляемые, уже отошли в прошлое, хотя когда-то именно они дали человеку возможность подняться в воздух. Впрочем, в некоторых случаях воздушные шары очень удобны, они используются и сейчас. Например, с аэростата удобно обучать прыжкам с. парашютом, а метеорологи исследуют давление, температуру и воздушные потоки в атмосфере с помощью шаров-зондов.
Задачи о воздушных шарах даются иногда на вступительных экзаменах. Обычно их можно разделить на два типа:
1) задачи, в которых нужно найти связь между габаритами и наполнением шара и подъемной силой, действующей на шар у поверхности Земли;
2) задачи, в которых нужно определить максимальную высоту подъема шара; при этом задается какая-нибудь модель атмосферы, то есть закон изменения давления и температуры с высотой.
По существу, задачи обоих типов – это задачи на статику. Для их решения нужно уметь применять уравнение состояния газов и найти условие равновесия шара, на который действует сила притяжения Земли и выталкивающая сила со стороны окружающего шар воздуха. Если выталкивающая сила больше силы притяжения (разность этих сил называют подъемной силой), шар поднимается вверх. Но по мере подъема уменьшается плотность окружающего воздуха, а, следовательно, уменьшается и выталкивающая сила, по закону Архимеда равная
где ρ — плотность воздуха, а V — объем шара. На некоторой высоте выталкивающая сила окажется равной силе притяжения – это и будет максимальной высотой подъема шара.
Разберем теперь несколько конкретных задач, которые в разные годы предлагались на вступительных экзаменах в Московский физико-технический институт.
Задача 1. Сферическая оболочка воздушного шара сделана из материала, квадратный метр которого имеет массу b = 1 кг/м2. Шар наполнен гелием при нормальном атмосферном давлении. При каком минимальном радиусе шар поднимает сам себя? Температура гелия и температура окружающего воздуха одинаковы и равны 0 ºС. Молекулярная масса воздуха 29 кг/кмоль, молекулярная масса гелия 4 кг/кмоль.
При увеличении радиуса шара выталкивающая сила растет пропорционально кубу радиуса, а вес оболочки – пропорционально квадрату радиуса. Следовательно, выталкивающая сила растет быстрее и, начиная с какого-то значения радиуса, станет больше, чем вес оболочки. Тогда шар начнет подниматься. Обозначим этот радиус оболочки через r. При этом
откуда
Плотности воздуха ρв и гелия ρНе при данных условиях найдем с помощью закона Менделеева–Клапейрона 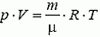
Окончательно получаем
Задача 2. Объем воздушного шара равен V = 230 м3, масса оболочки М = 145 кг. Шар наполнен горячим воздухом при нормальном атмосферном давлении. Какую температуру должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Температура наружного воздуха t0 = 0 оС.
При нагревании воздуха его плотность уменьшается, так как 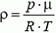
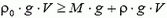
Отсюда
значит,
Tmin » 2T0 = 546 ºK = 273 ºC.
Задача 3. Для удержания на поверхности Земли метеорологического шара-зонда с массой М = 20 кг необходимо приложить силу F = 1000 Н. Шар поднимается до такой высоты, где его объем увеличивается в два раза. Температура воздуха, измеренная на этой высоте с помощью зонда, оказалась равной t = –43 ºС. Вычислить давление воздуха на этой высоте, если на поверхности Земли давление р0 = 754 мм рт. ст., а температура t0= +17 °С.
Условие равновесия шара у поверхности Земли записывается так:
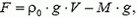
где V — объем шара у поверхности Земли, а 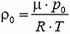
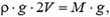
где 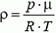
Задача 4. Шар-зонд, наполненный водородом, имеет герметичную оболочку постоянного объема V = 50 м3. Масса шара вместе с водородом М = 5 кг. Определить, на какую максимальную высоту он сможет подняться, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура в стратосфере t = –60 ºС. Молекулярная масса воздуха 29 кг/кмоль. Давление у поверхности Земли р0 = 1 атм.
На максимальной высоте выталкивающая сила равна весу шара- зонда:
Выразив плотность окружающего воздуха через давление и температуру, получим
Таким образом, давление воздуха на этой высоте равно
Посмотрим теперь, во сколько раз давление р меньше давления у поверхности Земли р0: 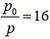
Из условия известно, что давление падает в два раза через каждые 5 км подъема, то есть 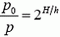
Отсюда
H = 4h = 20 км.
Задача 5. Нерастяжимая оболочка шара-зонда объема V = 75 м3 имеет в нижней части небольшое отверстие. Масса оболочки t = 7 кг. Шар наполнен водородом. Определить, на какую максимальную высоту сможет подняться этот шар-зонд, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура воздуха в стратосфере t = –60 °С, температура водорода равна температуре окружающего воздуха. Давление у поверхности Земли р0 = 1 атм.
Эта задача отличается от предыдущей тем, что оболочка шара не герметична, а имеет отверстие. Следовательно, давление внутри шара все время равно давлению в атмосфере, и по мере увеличения высоты подъема шара водород вытекает из отверстия. Будем, считать, что подъем происходит достаточно быстро и можно пренебречь диффузией воздуха внутрь оболочки, тогда условие равновесия шара на максимальной высоте
Плотности водорода и воздуха можно найти из уравнения Менделеева-Клапейрона:
Таким образом, давление на максимальной высоте
Отношение 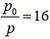
Высота подъема в задаче 5 получилась такая же, как для герметичного шара в задаче 4, но не следует забывать, что мы рассматривали разные шары, с разными объемами и массами. А если оба шара совершенно одинаковы и отличаются только тем, что у одного оболочка герметичная, а у другого имеет отверстие, — какой из шаров поднимется выше в этом случае?
Выталкивающая сила будет одинакова для обоих шаров, так как их объемы равны. Если начальные массы шаров были одинаковы, то после подъема шар с отверстием окажется легче, так как часть наполняющего его газа вытечет при подъёме. Следовательно, шар с отверстием сможет подняться на большую высоту.
Обычно человеку, впервые задумавшемуся над этим вопросом, такой результат кажется странным. Часто задают вопрос: «Как вообще в шаре с отверстием возникает подъемная сила? Ведь снизу, там, где отверстие, воздух и газ внутри шара находятся в равновесии».
Давайте рассмотрим верхнюю точку шара. Если в нижней точке шара давление воздуха и газа равно р0, в верхней точке давление воздуха 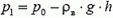
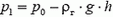
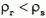
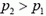
то, так как h мало — всего несколько метров, 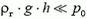
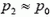
то здесь оба члена одинаковы по порядку величины, и учитывать их надо оба. Кстати сказать, то, что мы считаем ρв и ρг постоянными, — тоже приближение, на самом деле они уменьшаются с высотой по мере уменьшения давления. Но учет этого обстоятельства дал бы значительно меньшую поправку к выталкивающей силе, этой поправкой можно пренебречь.
Упражнения
1. Определить подъемную силу воздушного шара, в котором находится t г водорода. Оболочка шара герметичная и сделана из легкого неупругого материала, который может свободно растягиваться.
2. На сколько градусов надо нагреть воздух внутри сообщающегося с атмосферой воздушного шара, сферическая оболочка которого имеет диаметр 10 м и весит 10 кг, для того чтобы шар взлетел? Атмосферное давление 735 мм. рт. ст., температура окружающего воздуха +27 °С.
3. Воздушный шар представляет собой баллон постоянного объема, наполненный гелием. Через отверстие в нижней части шар сообщается с атмосферой. Как изменится максимальная высота подъема шара, если гелий нагреть до температуры t1? Температуру атмосферы считать постоянной и равной t0, а давление изменяющимся по закону 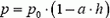
Ответы.
1. 13,5m·g.
2. Не менее чем на 5º.
3. 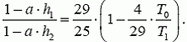
Как вычислить массу газа
Довольно часто встает вопрос: как можно вычислить массу какого-либо газа, содержащегося в определенном объеме при определенных условиях (давлении, температуре)? Произвести эти вычисления несложно, надо лишь знать несколько правил.

Инструкция
Предположим, перед вами поставлена задача: надо определить массу углекислого газа, занимающего при нормальном давлении и комнатной температуре объем в 0,18 м^3. Прежде всего вспомните универсальное правило, согласно которому 1 моль любого газа при нормальных условиях занимает объем, равный 22,4 литра. (Точнее – 22, 414 литра, но для упрощения расчетов эту величину можно округлить).
Потом переведите данный вам объем в литры. 0,18м^3 – это 180 литров. Соответственно, в нем содержится 180/22,4 = 8,036 молей углекислого газа.
А теперь остается последний шаг. Формула углекислого газа — СО2. Его молярная масса: 12 + 16*2 = 44 грамма/моль. То есть в одном моле углекислого газа содержится примерно 44 грамма этого вещества. Сколько же его в 8,036 молях? Произведите умножение: 44*8,036 = 353, 58 грамма или округленно 353,6 грамма. Задача решена.
Если вам надо найти массу того же углекислого газа, но находящегося при условиях весьма отличающихся от нормальных? Например, какое-то количество этого газа поместили в герметичный сосуд объемом V, нагрели до температуры Т, измерили его давление, оказавшееся равным P. Вопрос: какая масса углекислого газа содержится в сосуде при таких условиях?
И эта задача также очень простая. Для ее решения надо всего лишь вспомнить про уравнение Менделеева-Клапейрона, названное в честь двух выдающихся ученых. Оно было выведено ими для описания состояний так называемого «идеального газа». Его формула такова: PV = MRT/m. Или в слегка видоизмененной форме: PVm = МRT, где З – давление в паскалях, V – объем в кубических метрах, m – молярная масса газа, M – его фактическая масса, T – температура в градусах Кельвина, R – универсальная газовая постоянная, примерно равная 8,31.
Легко можно видеть, что фактическая масса газа М вычисляется по формуле: М = PVm / RT. Подставив в эту формулу все известные данные, и помня, что молярная масса углекислого газа m равна 44 грамма/моль, вы легко получите ответ.
Конечно же, ни углекислый газ, ни какой-либо другой не является идеальным газом. Поэтому, уравнение Менделеева-Клапейрона не вполне точно описывает его состояние. Но, если условия не очень сильно отличаются от нормальных, погрешности вычислений малы, и ими можно пренебречь.
Источники:
- формула углекислого газа
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Страница 58 из 84
§54. Воздухоплавание
Вопросы
1. Почему воздушные шары наполняют водородом или гелием?
Ответ:
Водород или гелий имеет меньшую плотность, по сравнению с воздухом. В итоге возникает сила Архимеда, поднимающая шар в воздухе.
2. Как рассчитать подъёмную силу шара, наполненного гелием?
Ответ:
По силе Архимеда ($F_{А}= gρ_{возд}V$) необходимо понять, какая масса воздуха находится в объеме шара и вычесть из этой массы массу газа в шаре и массу самого шара. Эта разница и станет показателем подъемной силой. ($P_{г} = gm_{г}, m_{г} = ρ_{г}V$).
3. Почему уменьшается выталкивающая сила, действующая на шар, по мере его подъёма?
Ответ:
Мы знаем, что для поднятия шара в воздух необходимо действие выталкивающей силы. $F_{А}$, действующей на шар. при этом ее действие должно превышать силу тяжести $F_{тяж}$, т. е. $F_{А}>F_{тяж}$ шара.
Кроме того, известно, что по мере поднятия шара меняется плотность атмосферы, слои становятся более разряженными, в итоге действие выталкивающей силы уменьшается. ($F_{А} = gρV$, ).
4. Как регулируют высоту подъёма воздушного шара, наполненного горячим воздухом?
Ответ:
Шар можно поднять с помощью горелки, которая устанавливается под отверстием внизу воздушного шара. В итоге, когда горелка подогревает воздух, то меняется его плотность, он становится более разряженным, так как молекулы реагируют друг с другом, сталкиваются, оказывают давление на стенки шара. Часть молекул воздуха либо вылетает вовсе из шара, либо за счет действия на стенки шара его объем увеличивается. То и другое влияет на плотность среды в шаре.
При уменьшении плотности, но сохранении объема шара, появляется подъемная сила, сила выталкивания. Она и поднимает шар вверх. При остывании воздуха плотность увеличивается, и/или шар становится меньшего объема. Шар теряет подъемную силу.
Упражнение 29
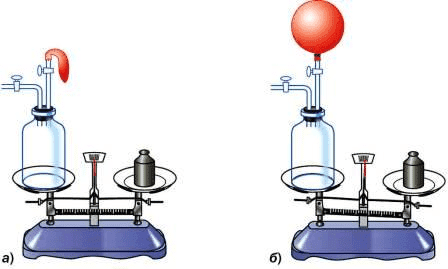
1. На весах уравновешена бутылка, внутри которой находится сжатый воздух. Через пробку бутылки пропущена стеклянная трубка с краном, к наружному концу которой привязана оболочка резинового шара (рис. 162,а). Если часть воздуха из бутылки перейдёт в оболочку и раздует её (рис. 162,б), то равновесие весов нарушится. Объясните наблюдаемое явление.
рис. 162
Ответ:
В нашем случае при открытии крана произойдет увеличение объема тела (бутылка и шарик) и воздух из бутылки частично уйдет в шарик. В итоге получается, что произойдет изменение плотности этого тела (бутылка и шарик). Сила выталкивания изменится.
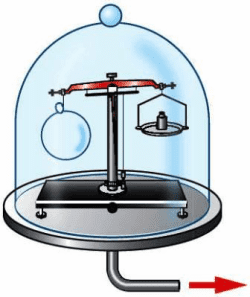
2. На весах уравновесили лёгкий стеклянный шарик. Затем весы поместили под колокол воздушного насоса и откачали воздух. Равновесие весов нарушилось (рис. 163). Почему?
рис. 163
Ответ:
Мы знаем, что сила Архимеда она же выталкивающая сила зависит от среду в которую погружаем тело, от ее плотности, а также от массы и объема погружаемого тела. При этом изменение любой из этих характеристик приведет к изменению баланса. В нашем случае мы изменим плотность среды, в которую погрузили тело (стеклянный шар). В итоге, выталкивающая сила стала меньше, ведь она была равна массе среды в объеме тела (стеклянный шар). Шар потерял выталкивающую силу, весы разбалансировались.
3. Один шарик надут воздухом, другой — водородом, третий — углекислым газом. Какие шарики не взлетят? Объясните почему.
Ответ:
$ρ_{возд}$ = 1290 кг/$м^{3}$;
$ρ_{вод}$ = 90 кг/$м^{3}$;
$ρ_{угл}$ = 1980 кг/$м^{3}$.Нам необходимо найти значение силы Архимеда и понять, будет ли она подъемной или нет. Возникнет ли выталкивающая сила?
Если $F_{А}$, действующая на шар будет больше силы тяжести$F_{тяж}$, то есть$F_{А}$ >$F_{тяж}$, то возникнет выталкивающая сила.
Получается так, если ниже плотность газа, заполняющего воздушный шар в данном объёме, тем меньше действующая на него сила тяжести, тем больше подъёмная сила!
При этом газы с меньшей, чем у воздуха плотностью будут обладать такой выталкивающей силой.Получается:
Шар надутый водородом, взлетит, так как плотность водорода ниже плотности воздуха.
Шар надутый углекислым газом, не взлетит, так как плотность углекислого газа выше плотности воздуха.
Шар надутый воздухом, не взлетит, так как вес оболочки шарика с учётом веса воздуха выше веса окружающего воздуха.
Как найти массу газа в баллоне?
#37026
2020-03-24 14:18 GMT
Есть баллон с метаном, объемом 210 литров, с давлением 24,5 МПа! Какая масса газа уместиться в такой баллон? Желательно с формулами и пояснениями к ним
#37028
2020-03-24 15:34 GMT
#37026
РоманУфа :Есть баллон с метаном, объемом 210 литров, с давлением 24,5 МПа! Какая масса газа уместиться в такой баллон? Желательно с формулами и пояснениями к ним
Вот вам формула с пояснениями:

Отсюда (m=frac{PVM}{RT}).
Для метана (M=0.016;frac{кг}{моль} ).
Как видите, нужно ещё знать температуру. Чем больше температура, тем меньше масса газа.
Подставляете числа в формулу и считаете.
#37029
2020-03-24 16:56 GMT
#37028
zam :#37026
РоманУфа :Есть баллон с метаном, объемом 210 литров, с давлением 24,5 МПа! Какая масса газа уместиться в такой баллон? Желательно с формулами и пояснениями к ним
Вот вам формула с пояснениями:

Отсюда (m=frac{PVM}{RT}).
Для метана (M=0.016;frac{кг}{моль} ).
Как видите, нужно ещё знать температуру. Чем больше температура, тем меньше масса газа.
Подставляете числа в формулу и считаете.
А в каких единицах измерения подставлять значения???
#37031
2020-03-24 17:32 GMT
#37029
РоманУфа :А в каких единицах измерения подставлять значения???
Главное, что бы все в одной системе. Наиболее популярная — Си.
Тогда (P = 24.5; МПа = 2.45 cdot 10^7 ; Па),
(V=0.21; м^3)
,
(T=293;K)
(нормальная комнатная температура).
#37032
2020-03-24 18:26 GMT
#37031
zam :#37029
РоманУфа :А в каких единицах измерения подставлять значения???
Главное, что бы все в одной системе. Наиболее популярная — Си.
Тогда (P = 24.5; МПа = 2.45 cdot 10^7 ; Па),
(V=0.21; м^3)
,(T=293;K)
(нормальная комнатная температура).Огромное спасибо за помощь
#37041
2020-03-25 09:37 GMT
zam, тут давление больно высокое.
245 атмосфер.
У Метан Tk=190,65 К Pk=45,8 атмосферы
Плохо помню какие есть методы исследовани я веществ в критическом состоянии и как они себя видут, но думается там уже будет жидкость, а не пар.
Относительный удельный вес жидкого метана 0,555
210 Л *0,555= 116,55 кг.

#37047
2020-03-25 12:31 GMT
#37041
Очепятка :но думается там уже будет жидкость, а не пар.
В задании сказано: «Какая масса газа…».
Так что, условия там такие, что метан в газообразном состоянии.
#37053
2020-03-25 13:49 GMT
#37047
zam :#37041
Очепятка :но думается там уже будет жидкость, а не пар.
В задании сказано: «Какая масса газа…».
Так что, условия там такие, что метан в газообразном состоянии.
Так Вы фразу целиком читайте. «Какая масса газа уместиться в такой баллон?»
Это не значит, что газ в болоне, это значит что закачиваем мы газ. А балон такой что сжимает газ до жидкого состояния.