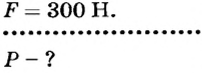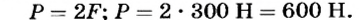Задача № 107
Два груза m1=1кг
и m2=0,5
кг связаны
легким шнуром, перекинутым через блок
(рис.). Блок радиусом R=10
см вращается
с угловым ускорением ε=20
рад/с2.
Найти массу
блока, если она равномерно распределена
по его ободу.
Дано:
,
,
,
Найти:
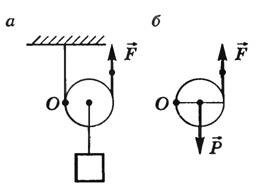
Рисунок:

Решение:
Применим
при решении задачи основные законы
поступательного движения. На каждый из
движущихся грузов действуют две силы:
сила тяжести

,
направленная
вниз, и сила Т
натяжения нити,
направленная
вверх.
Груз
по
условию задачи в 2 раза меньше по массе
чем груз
.
Следовательно груз
будет двигаться вверх с ускорением
.
А груз
будет двигаться вниз с ускорением
.
Так
как вектор ускорения
груза
направлен
вверх, то:
(1)
Равнодействующая
этих сил вызывает равноускоренное
движение и, по второму закону Ньютона,
равна:
(2)
Из
формулы (2) получаем:
(3)
Вектор
ускорения
груза
направлен
вниз, следовательно:
(4)
Равнодействующая
этих сил вызывает равноускоренное
движение и, по второму закону Ньютона,
равна:
(5)
Из
формулы (5) получаем:
(6)
Согласно
основному закону динамики вращательного
движения, вращающий момент
,
приложенный к блоку, равен произведению
момента инерции
блока на его угловое ускорение
:
(7)
Определим
вращающий момент. Силы натяжения нитей
действуют не только на грузы, но и на
блок. По третьему закону Ньютона, силы
и
,
приложенные к ободу блока, равны
соответственно силам
и
,
но по направлению им противоположны.
При движении грузов блок ускоренно
вращается против часовой стрелке.
Следовательно,
.
Вращающий
момент, приложенный к блоку, равен
произведению разности этих сил на плечо,
равное радиусу блока R,
т.е.:
(8)
Момент
инерции блока в виде колеса, масса
которого равномерно распределена по
ободу:
(9)
Угловое
ускорение блока связано с линейным
ускорением грузов соотношением:
(10)
Подставим
в формулу (7) формулы (8), (9) и (10):
(11)
Из
формулы (11) получаем:
(12)
Так
как
и
,
то подставим формулы (3) и (6) в формулу
(12):
(13)
Преобразуем
формулу (13) к виду:
или
с учетом формулы (10):
(14)
Из
формулы (14) выразим массу блока и найдем
её:

Ответ:

Соседние файлы в папке Вариант №7
- #
- #
- #
- #
- #
- #
- #
Преподаватель который помогает студентам и школьникам в учёбе.
Блоки в физике — виды, формулы и определения с примерами
Содержание:
Блоки:
Всегда ли удобно использовать рычаг
Поднять груз на значительную высоту с помощью рычага очень сложно. Чем высота больше, тем длиннее должен быть рычаг. Такого недостатка нет у блока.
Что такое блок
Блок — это устройство, состоящее из веревки, переброшенной через колесо, которое может вращаться на оси.
Обод колеса, как правило, имеет желоб, в котором прокладывается трос или веревка.
Ось блока может быть неподвижной или перемещаться вместе с колесом. В связи с этим блоки бывают подвижными и неподвижными.
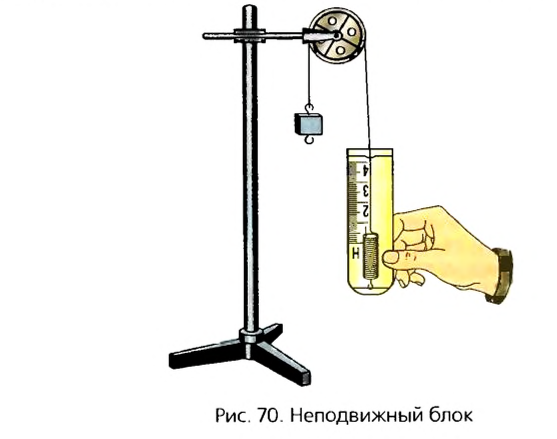
Какой блок называют неподвижным
У неподвижного блока ось вращения не изменяет своего положения в пространстве. Она с помощью специальной обоймы закреплена на балке или на другой опоре (рис. 70). Если на конец веревки, переброшенной через блок, подействовать силой, то другой конец начнет двигаться вверх. Если к этому концу прикрепить груз определенной массы, то он будет подниматься вверх. Если на свободный конец веревки действует сила, направленная вниз, то на груз действует сила, направленная вверх. Измерение этих сил показывает, что они равны.
Почему неподвижный блок не дает выигрыша в силе
Неподвижный блок выигрыша в силе не дает, он только изменяет направление действия силы.
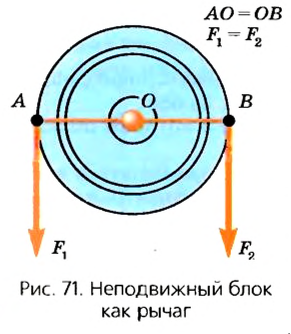
Такую особенность можно легко объяснить, учитывая, что неподвижный блок похож на равноплечий рычаг. Для этого перенесем точки действия сил вверх к точкам А к В, где веревка касается блока (рис. 71). Плечи этих сил OA и ОВ будут одинаковыми, как радиусы окружности. Согласно условию равновесия рычага силы F1 и F2 также должны быть одинаковыми. Опыт подтверждает эти выводы.
- Заказать решение задач по физике
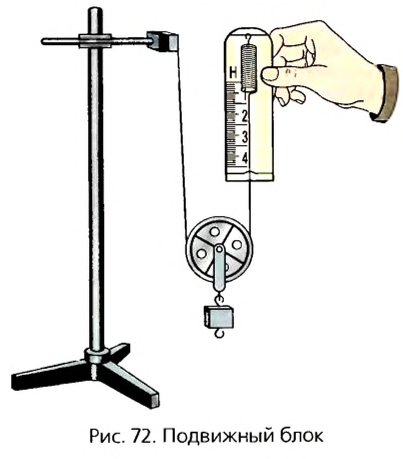
Какой блок называют подвижным
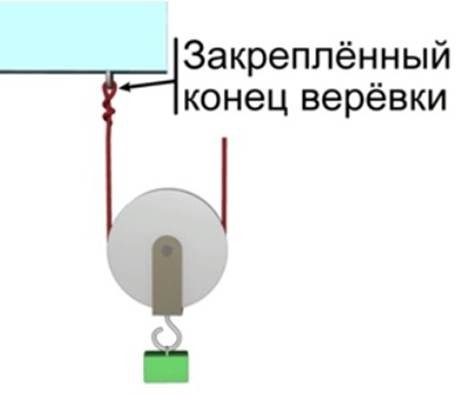
Подвижным называют блок, ось которого перемещается в пространстве. При использовании такого блока обычно один конец веревки или троса закрепляют на опоре, а груз — на обойме, в которой блок закреплен. На рисунке 72 показан опыт с таким блоком. К оси легкого подвижного блока подвешен груз массой 102 г. Итак, на ось блока действует сила 1 Н. Стрелка динамометра, присоединенного к свободному концу веревки, показывает примерно 0,5 Н. Некоторые небольшие различия связаны с тем, что блок сам имеет вес и на него действует сила трения.
Почему подвижный блок дает выигрыш в силе
Такую особенность подвижного блока можно объяснить, учитывая свойства рычага (рис. 73). Диск блока можно считать рычагом длиной 2R (где R — радиус колеса). Ось вращения такого рычага проходит через точку А на ободе колеса, а точками приложения сил являются точки О и В. Так как 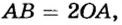
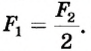
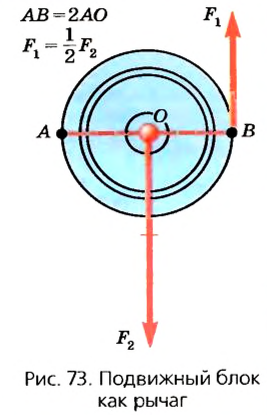
Пример решения задачи
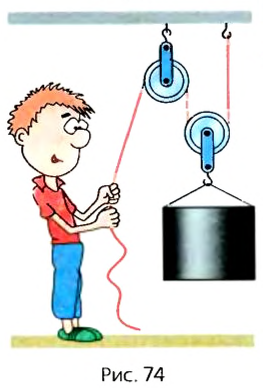
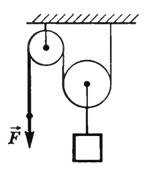
Определить вес груза, который удерживается системой подвижного и неподвижного блоков, если на свободный конец троса действует сила 300 Н (рис. 74).
Дано:
Решение
Неподвижный блок выигрыша в силе не дает. Поэтому вычисления производим с учетом только подвижного блока, который дает выигрыш в силе в два раза. О массе блока в условии задачи не сказано, поэтому весом блока можно пренебречь по сравнению с весом груза. Таким образом,
Ответ. Вес груза равен 600 Н.
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Давление газов и жидкостей
- Движение жидкостей и газов
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Столкновения в физике
- Рычаг в физике
приложенная сила — 250 H
выигрыш в силе на подвижном блоке 2раза
значит сила подъема F=2*250 =500 H
вес груза P = mr*g =40*10=400 Н
если подъм равномерный ,то
масса блока m=(F-P)g =(500-400)/10=100/10=10 кг
кпд = P/F *100% = 400/500*100%=80%
Простыми словами: блок – это колесо, на окружности которого есть желобок. Колесо может вращаться вокруг своей оси, а в желоб можно проложить ремень, или веревку.
Например, велосипедное колесо можно считать блоком, если с него снять резиновую шину и вместо нее проложить в желоб веревку, канат и т. п. К одному концу веревки можно прикрепить груз, а за второй конец – тянуть, то есть, прикладывать к нему силу.
Если вместо веревки желают использовать цепь, то вместо колеса с желобом часто используют колесо с выступающими зубцами. Это исключает проскальзывание цепи и увеличивает сцепление. Такие конструкции называют звездочками. К примеру, велосипед содержит две звезды – одну ведущую, на оси с педалями, вторую – ведомую, на оси заднего колеса.
Блоки применяют в различных механизмах, например, для подъема грузов.
Чем шкив отличается от блока
Есть разница между шкивом и блоком при их внешнем сходстве.
Шкив — соединяется с осью жестко, он будет передавать вращательное усилие с оси на ремень, или с ремня на ось.
Блок — свободно вращается на оси, с оси на ремень или с ремня на ось вращательное усилие не передаёт.
Условия для вывода формул
Упростим задачу получения формул для блоков. Будем считать блок идеальным.
Пусть для этого выполняются некоторые условия:
- считаем, блок невесомым, то есть, у него нет массы,
- считаем, что блок абсолютно жесткий, то есть, нет его деформации,
- при вращении блока трение отсутствует.
Пояснения к условиям
Эти три условия нужны для того, чтобы наши усилия затрачивались только на перемещение полезного груза, и не затрачивались на вращение блока. Груз мы прикрепляем к одному концу веревки, в то время, как тянем за другой ее конец.
Более строгим языком: условия должны выполняться, чтобы приложенная сила совершала лишь работу по перемещению полезного груза, а энергия на вращение блока не затрачивалась.
Честно говоря, в реальности ничего идеального не существует и все эти условия полностью соблюсти нельзя. Блоки изготавливают из прочных металлов, а они обладают массой. Трение можно только лишь уменьшить, но совсем избавиться от него не получится. Но, так как масса блока мала, по сравнению с поднимаемым грузом и трение значительно уменьшено, будем в этой статье считать блок идеальным.
Рассмотрим такие идеальные блоки.
Два вида блоков
Блоки, по их перемещению, можно разделить на два вида.
Неподвижный блок – вращается, оставаясь на месте (вращающееся колесо велосипеда, к примеру, лежащего на боку).
Подвижный блок – вращается и движется поступательно (велосипедное колесо во время поездки на велосипеде).
Примечание:
Если говорить более строгим языком, то через центр блока перпендикулярно плоскости блока проходит ось вращения. Блок называют неподвижным, если при вращении блока вокруг оси, точки, лежащие на этой оси, остаются неподвижными. Если же, точки, лежащие на оси, проходящей через центр блока, при его вращении будут двигаться поступательно — блок назовут подвижным.
Неподвижный блок
Рассмотрим блок, изображенный на рисунке 1.
Рис. 1. Неподвижный блок может вращаться вокруг красной точки в центре. Силы приложены к точкам черного цвета, слева и справа от центральной точки
Назовем красную точку на рисунке 1 кратко «точкой вращения». Блок может вращаться вокруг этой точки. При этом все точки блока будут двигаться по окружностям вокруг красной точки, а красная точка будет оставаться неподвижной.
Примечание:
Через точку, обозначенную на рисунке 1 красным цветом, проходит ось вращения блока перпендикулярно плоскости рисунка.
К левой части веревки, нарисованной черным цветом и пропущенной через желобок, приложена сила ( F_{1} ), а к правой части веревки – сила ( F_{2} ). Обе силы на рисунке направлены вниз.
Соединим три отмеченные точки прямой линией. На ней отметим расстояние между точкой, вокруг которой блок вращается и, точками, к которым приложены силы.
Рис. 2. Диаметр окружности соединяет три точки неподвижного блока, отмечены расстояния между точками приложения сил и осью вращения
Теперь для упрощения уберем с рисунка 2 некоторые элементы, получим картину, представленную на рисунке 3. То есть, мы заменили неподвижный блок рычагом.
Рис. 3. Неподвижный блок заменили рычагом, силы приложены по разные стороны от точки (оси), вокруг которой блок может вращаться
Определим вращательный момент каждой силы:
(M_{1} = F_{1} cdot R)
(M_{2} = F_{2} cdot R )
Подробнее о моменте силы читайте здесь (откроется в новой вкладке).
Теперь запишем условие равновесия рычага:
[-M_{1} + M_{2} = 0]
Пояснения к условиям равновесия рычага читайте в этой статье (откроется в новой вкладке).
И, подставив выражения для сил и их плеч, получим
( — F_{1} cdot R + F_{2} cdot R = 0)
( F_{2} cdot R = F_{1} cdot R )
Сократив обе части на ( R ), запишем для неподвижного блока следствие из условия равновесия:
[ large boxed { F_{2} = F_{1} } ]
Сила – это вектор, если между двумя векторами стоит знак равенства, значит, у них совпадают длина и направление.
О равенстве векторов читайте тут (откроется в новой вкладке).
Например, чтобы поднять мешок 50 килограммов без блока, нужно приложить силу примерно 500 Ньютонов. Используя неподвижный блок, мы прикладываем эту же силу, но благодаря блоку направляем ее вниз, а не наверх. Тянуть вниз удобнее, потому, что мы дополнительно прикладываем свой вес к тому концу веревки, за который тянем. Мы тянем вниз, а подвешенный мешок при этом поднимается вверх.
Важно! Неподвижный блок меняет направление вектора силы
Подвижный блок
Рассмотрим рисунок 4. На нем изображен подвижный блок. Он может вращаться вокруг точки, обозначенной на рисунке 4 красным цветом. Красную точку назовем «точкой вращения».
Рис. 4. Неподвижный блок может вращаться вокруг красной точки, расположенной на краю блока. Точки приложения сил (черные) лежат по одну сторону от точки, вокруг которой блок может вращаться
Проведем прямую линию через три отмеченные точки (рис. 5) и отметим на ней расстояния между точкой, вокруг которой блок вращается и, точками, к которым приложены силы.
Рис. 5. Диаметр окружности соединяет три точки подвижного блока, отмечены расстояния между точками приложения сил и осью вращения
Уберем с рисунка окружность и получим такую картину (рис. 6). Мы заменили подвижный блок рычагом. Обе точки приложения сил находятся по одну сторону от оси вращения. Подробнее о таких видах рычагов читайте по этой ссылке.
Рис. 6. Подвижный блок заменили рычагом, силы приложены по одну сторону от точки (оси), вокруг которой блок может вращаться
Вращательные моменты сил:
(M_{1} = F_{1} cdot 2 cdot R)
(M_{2} = F_{2} cdot R )
Теперь запишем условие равновесия рычага:
[M_{1} + (- M_{2} ) = 0]
Подставляя выражения для сил и их плеч, получим
( F_{1} cdot 2 cdot R — F_{2} cdot R = 0)
( F_{1} cdot 2 cdot R = F_{2} cdot R )
Разделим обе части на ( R ), и получим для подвижного блока следствие из условия равновесия:
( F_{1} cdot 2 = F_{2} )
Или же
[ large boxed { F_{1} = frac{F_{2}}{2} } ]
Из выражения видно, что сила, с которой нужно тянуть вверх, в два раза меньше силы, приложенной к центральной части блока.
Из рисунков 4 – 6 видно: чтобы поднять груз вверх, нужно так же, тянуть вверх.
Поднимая мешок массой 50 килограммов без блока, мы прикладываем силу примерно 500 Ньютонов. Используя подвижный блок, мы прикладываем силу 250 Ньютонов, это в 2 раза меньше, чем без блока. Направляем силу для подъема вверх, как и без блока.
Важно! Подвижный блок меняет модуль вектора силы
Способ быстро запомнить условие для подвижного блока: Вверх тянут две веревки, а вниз – одна (см. рис 4). Блок находится в равновесии, когда
Совместное усилие двух веревок, тянущих вверх = силе одной веревки, тянущей вниз
Для подвижного блока справедливо утверждение: во сколько раз выиграем в силе, во столько же раз проиграем в расстоянии. Если получаем выигрыш в силе в 2 раза, то проигрываем в расстоянии в 2 раза. Значит, чтобы поднять такой конструкцией груз на 1 метр, нужно вытянуть 2 метра веревки
Нужно запомнить
Сила – это вектор. У любого вектора две главные характеристики: длина и направление.
Подробнее о характеристиках векторов можно прочитать здесь.
Неподвижный блок – изменяет вектор силы по направлению.
Подвижный блок – изменяет вектор силы по величине (по модулю) т. е. длину вектора.
Комбинации блоков
Если подвижный и неподвижный блоки соединить так, как показано на рисунке 7, то получим устройство, которое позволяет получить выигрыш в 2 раза. На рисунке малый блок – неподвижный, большой – подвижный. Размеры блоков для такого их соединения не имеют значения.
Рис. 7. Скомбинировав таким образом подвижный и неподвижный блоки, можно получить выигрыш в силе в 2 раза
А если соединить так, как показано на рисунке 8, получим выигрыш в силе в 3 раза. Если получаем выигрыш в силе в 3 раза, то в 3 раза проигрываем в расстоянии. Значит, чтобы поднять такой конструкцией груз на 1 метр, нужно протянуть 3 метра веревки.
Малый блок на рисунке – неподвижный, большой – подвижный. Соотношение размеров блоков для такого их соединения не будет иметь большого значения, если расстояние между блоками будет намного превышать размеры самих блоков.
Рис. 8. Скомбинировав подвижный и неподвижный блок таким образом, можно получить выигрыш в силе в 3 раза. На рисунке малый блок – неподвижный, большой — подвижный
Важно! Применяя любые комбинации блоков, мы не получим выигрыша в работе. Если выигрываем в силе, то во столько же раз проигрываем в расстоянии!
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Подвижный блок отличается от неподвижного тем, что его ось не закреплена, и он может подниматься и опускаться вместе с грузом.
Рисунок 1. Подвижный блок
Как и неподвижный блок, подвижный блок состоит всё из того же колеса с желобом для троса. Однако здесь закреплен один конец троса, а колесо подвижно. Колесо движется вместе с грузом.
Как заметил ещё Архимед, подвижный блок по сути является рычагом и работает по тому же принципу, давая выигрыш в силе за счёт разницы плеч.
Рисунок 2. Силы и плечи сил в подвижном блоке
Подвижный блок перемещается вместе с грузом, он как бы лежит на веревке. В таком случае точка опоры в каждый момент времени будет находиться в месте соприкосновения блока с веревкой с одной стороны, воздействие груза будет приложено к центру блока, где он и крепится на оси, а сила тяги будет приложена в месте соприкосновения с веревкой с другой стороны блока. То есть плечом веса тела будет радиус блока, а плечом силы нашей тяги — диаметр. Правило моментов в этом случае будет иметь вид:
$$mgr = F cdot 2r Rightarrow F = mg/2$$
Таким образом, подвижный блок дает выигрыш в силе в два раза.
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис. 3). Неподвижный блок применяется только для удобства. Он, изменяет направление действия силы, позволяет, например, поднимать груз, стоя на земле, а подвижный блок обеспечивает выигрыш в силе.
Рисунок 3. Комбинация неподвижного и подвижного блоков
Мы рассмотрели идеальные блоки, то есть такие, в которых не учитывалось действие сил трения. Для реальных же блоков необходимо вводить поправочные коэффициенты. Используют такие формулы:
Неподвижный блок
$F = f • mg $
Подвижный блок
$F = f • 1/2 mg $
В этих формулах: $F$ — прилагаемое внешнее усилие (обычно это сила рук человека), $m$ — масса груза, $g$ — коэффициент силы тяжести, $f$ — коэффициент сопротивления в блоке (для цепей примерно 1,05, а для верёвок 1,1).
«Подвижный блок» 👇
Задача 1
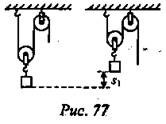
С помощью системы из подвижного и неподвижного блоков грузчик поднимает ящик с инструментами на высоту $S_1$ = 7 м, прикладывая силу $F$ = 160 Н. Какова масса ящика, и сколько метров верёвки придётся выбрать, пока груз поднимется? Какую работу выполнит в результате грузчик? Сравните её с работой, выполненной над грузом по его перемещению. Трением и массой подвижного блока пренебречь.
Решение
Дано:
$F$ = 160 H
$S_1$ = 7 м
$m, S_2 , A_1 , A_2$ — ?
Подвижный блок даёт двойной выигрыш в силе и двойной проигрыш в перемещении. Неподвижный блок не даёт выигрыша в силе, но меняет её направление. Таким образом, приложенная сила будет вдвое меньше веса груза: $F = 1/2P = 1/2mg$, откуда находим массу ящика: $m=frac{2F}{g}=frac{2cdot 160}{9,8}=32,65 кг$
Перемещение груза будет вдвое меньше, чем длина выбранной верёвки:
[S_2=2S_1=2cdot 7=14 м]
Выполненная грузчиком работа равна произведению приложенного усилия на перемещение груза: $A_2=Fcdot S_2=160cdot 14=2240 Дж $.
Работа, выполненная над грузом:
[A_1=mgS_1=32,65cdot 9,8cdot 7=2240 Дж]
Ответ: Масса ящика 32,65 кГ. Длина выбранной верёвки 14 м. Выполненная работа равна 2240 Дж и не зависит от способа подъёма груза, а только от массы груза и высоты подъёма.
Задача 2
Какой груз можно поднять с помощью подвижного блока весом 20 Н, если тянуть веревку с силой 154 Н?
Решение
Дано:
$Р_Б$ = 20 Н
$F$ = 154 H
$f$ = 1,1
$P$ — ?
Запишем правило моментов для подвижного блока: $F = f • 1/2 (P+ Р_Б)$, где $f$ — поправочный коэффициент для верёвки.
Тогда $P=2frac{F}{f}-P_Б=2cdot frac{154}{1,1}-20=260 Н$
Ответ: Вес груза 260 Н.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме