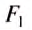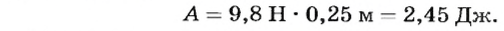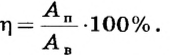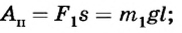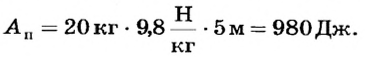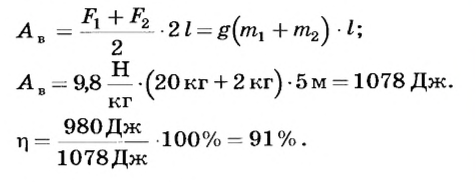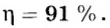В гидравлическом прессе площадь малого поршня 5
с
м
2
, площадь большого — 500
с
м
2
. Сила, действующая на малый поршень, 400 Н, на большой — 36 кН. Какой выигрыш в силе даёт этот пресс? Почему пресс не даёт максимального (наибольшего) выигрыша в силе? Какой выигрыш в силе должен был бы давать этот пресс при отсутствии силы трения между поршнем и стенками пресса?
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §49. Упражнение 25. Номер №2
Решение
Дано:
S
1
= 5
с
м
2
;
S
2
= 500
с
м
2
;
F
1
= 400 Н;
F
2
= 36 кН;
Найти:
F
2
F
1
− ?
S
2
S
1
− ?
Решение:
Выигрыш в силе с учётом силы трения:
F
2
F
1
=
36000
400
= 90;
Максимальный выигрыш в силе в отсутствие силы трения:
S
2
S
1
=
500
5
= 100.
Пресс не даёт максимального (наибольшего) выигрыша в силе, так как часть силы теряется на преодоление силы трения.
Ответ. 90; 100.
Random converter
- Калькуляторы
- Механика
Калькулятор выигрыша в силе
Этот мощный болторез представляет собой одновременно работающие четыре рычага первого рода
Калькулятор определяет выигрыш в силе для реального простейшего механизма.
Пример: Сила 50 Н приложена к простейшему механизму, который поднял груз весом 465 Н. Рассчитать идеальный и реальный выигрыш, если КПД механизма 75%.
Входные данные
Коэффициент полезного действия
η %
СилаСкоростьРасстояние
На входе
in
На выходе
out
Поделиться ссылкой на этот калькулятор, включая входные параметры
Выходные данные
Идеальный выигрыш в силе (IMA)
Реальный выигрыш в силе (AMA)
Определения и формулы
Простейшие механизмы
Принципы простейших механизмов
Выигрыш в силе идеального простейшего механизма
Коэффициент полезного действия
Авиационный турбовинтовой двигатель PT6-A50. Университет Торонто
Определения и формулы
Простейшие механизмы
Для большинства людей механизмы — сложные машины вроде банкоматов, холодильников, автомобилей или самолетов. Однако любое устройство, которое передает или изменяет силу или момент силы для определенных целей может быть названо механизмом. Например, винт или обычное колесо являются механизмами. Простейшие механизмы — это устройства с одной-двумя движущимися частями либо вообще без них, которые используются для выполнения работы путем изменения силы или движения. Это простейшие устройства, которые используют выигрыш в силе для ее увеличения. Такие устройства называют простейшими механизмами.
Ученые эпохи Возрождения определили шесть простейших механизмов (в алфавитном порядке): блок, винт, ворот, клин, наклонная плоскость и рычаг. Можно сказать, что в составе большинства современных механизмов и машин в качестве «кирпичиков» входят простейшие механизмы. Конечно, бывают машины и механизмы, в которых используются не только механические силы, но и ядерные или электромагнитные силы. Можно даже отметить, что подавляющее большинство физических сил в классической механике имеет электромагнитную природу. Однако здесь мы ограничимся рассуждениями только о механизмах, действие которых зависит только от сил гравитации и сил, изучаемых в классической механике.
Ротационная печатная машина, ок. 1870 г. Музей науки в Лондоне
Принципы простейших механизмов
Выигрыш в силе идеального простейшего механизма
Выигрыш в силе (механический эффект) для различных простейших механизмов рассчитывается по-разному. Однако приведенные ниже расчеты относятся к любому из простейших механизмов. Для идеального простого механизма с линейным перемещением, выигрыш в силе представляет собой отношение силы на выходе механизма к силе на его входе:
где MA — выигрыш (сокращение от англ. mechanical advantage), Fin — сила, приложенная на входе механизма и Fout — сила на выходе механизма. Это идеальный или теоретический выигрыш (IMA, от англ. ideal mechanical advantage). Он зависит только от физических размеров механизма и определяет его максимальную производительность.
Поскольку для любого механизма справедлив закон сохранения энергии, в идеальном механизме, где нет трения или упругой деформации, выходная мощность Pout всегда равна входной мощности Pin:
Мы знаем, что мощность — это физическая величина, равная скорости выполнения работы или преобразования энергии, следовательно
Для любого простейшего механизма правило сохранения энергии можно переписать в виде
А это, в свою очередь, можно записать в виде
Из этих уравнений можно сделать вывод, что выигрыш в силе идеального механизма равен отношению входной скорости к выходной скорости перемещения деталей механизма:
Поскольку скорость определяется как быстрота перемещения тела, можно записать
и
20-тонный маховик парового двигателя ткацкой фабрики мощностью 700 л. с., изготовленного в 1903 г.; в течение 67 лет двигатель приводил в движение сотни ткацких станков с помощью приводных ремней; Музей науки в Лондоне
Коэффициент полезного действия
КПД простейшего механизма определяется как отношение мощности на выходе к мощности на входе механизма:
Одноцилиндровый газовый двигатель внутреннего сгорания, запатентованный бельгийским инженером Этьеном Ленуаром и построенный в Англии в 1865 г. Это первый двигатель внутреннего сгорания, который работал на газе, подаваемом в города для освещения, и которому не нужны были уголь и вода, без которых не могли работать паровые двигатели
Он измеряет степень уменьшения мощности в реальном механизме за счет трения и других факторов, которые всегда имеются в неидеальном механизме, относительно идеальной теоретической максимальной мощности, когда Pin = Pout. Другие факторы включают упругую деформацию и износ деталей механизма. КПД идеального механизма равно 100%. Как мы уже говорили, мощность равна произведению силы на скорость, следовательно КПД равен выигрышу, деленному на отношение скоростей:
Следовательно, для неидеального механизма реальный выигрыш (AMA от англ. actual mechanical advantage) зависит от КПД так:
Теперь можно записать уравнение связи идеального и реального выигрыша с КПД:
Другие калькуляторы простейших механизмов:
- Калькулятор выигрыша в силе наклонной плоскости
- Калькуляторы рычага
- Калькулятор выигрыша в силе, даваемого полиспастом
- Калькулятор выигрыша в силе винта
- Калькулятор выигрыша в силе, даваемого клином
- Калькулятор выигрыша в силе, даваемого воротом
Механика
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
В гидравлическом прессе площадь малого поршня 5 см2, площадь большого – 500 см2. Сила, действующая на малый поршень, 400 Н, на большой – 36 кН. Какой выигрыш в силе даёт этот пресс? Почему пресс не даёт максимального (наибольшего) выигрыша в силе? Какой выигрыш в силе должен был бы давать этот пресс при отсутствии силы трения между поршнем и стенками пресса?
|
Ответ: |
|
| Дано: | Решение |
|---|---|
|
`S_1 = 5″ см»^2` `S_2 = 500″ см»^2` `F_1 = 400 Н` `F_2 = 36″ кН» = 36*10^3 Н` |
`F_2/F_1 = (36*10^3 Н)/(400 Н) = 90` `S_2/S_1 = (500″ см»^2)/(5″ см»^2) = 100` |
| Найти: | |
|
`F_2/F_1 = ?` `S_2/S_1 = ?` |
Пресс не даёт максимального выигрыша в силе, потому что между поршнем и стенками пресса присутствует сила трения, на преодоление которой тратится сила, действующая на малый поршень.
При отсутствии силы трения между поршнем и стенками пресса выигрыш в силе был бы равен 100 (отношению площадей большого и малого поршней).
Содержание:
Золотое правило механики:
Используя простые механизмы, можно изменять как силу, приложенную к телу, так и путь, от которого зависит значение работы. Означает ли это, что с помощью простых механизмов можно получить выигрыш в работе?
Теоретические сведения
В технике, на производстве и в повседневной жизни используют простой механизм, который называется наклонная плоскость. Это устройство, в котором длинная доска или рейка положена так, что образует некоторый угол с горизонтом. Как правило, этот угол меньше 45о.
Использование наклонной плоскости позволяет получить выигрыш в силе. Выигрыш в работе, как утверждает «золотое правило» механики, получить невозможно. В реальных условиях тот, кто пользуется наклонной плоскостью, даже проигрывает в работе, поскольку при перемещении тела но наклонной плоскости выполняется дополнительная работа по преодолению трения.
Золотое правило механики
Рассмотренные нами простые механизмы применяют при выполнении работы в тех случаях, когда нужно меньшей силой уравновесить большую. Тогда перед нами встаёт вопрос: Простые механизмы дают выигрыш в силе, а дают ли они выигрыш в работе ?
Уравновесим рычаг, приложив к нему две разные по значению силы
Видим, что теперь в правиле рычага можно заменить отношение плечей сил на отношение путей точек приложения сил, тогда получим: 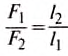
По определению механической работы: 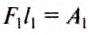
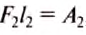
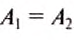
Рычаг выигрыша в работе не даёт.
Это касается и других простых механизмов.
Ни один из простых механизмов не даёт выигрыша в работе: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии.
Это правило назвали «золотым правилом» механики.
Дает ли выигрыш в работе простой механизм
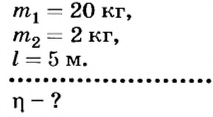
Закрепим конец нити на крючке динамометра и прикрепим к ней груз массой 1 кг (рис.124). Начнем равномерно поднимать его вверх. Динамометр покажет, что к нити приложена сила 9,8 Н. Поднимем груз на высоту 0,25 м и рассчитаем работу, которая при этом будет выполнена:
Конец нити закрепим неподвижно на штативе и пропустим ее через подвижный блок, к которому прикреплен груз массой 1 кг.
К свободному концу нити прикрепим динамометр и обозначим на линейке положение точки присоединения динамометра (рис. 125). Постепенно будем поднимать динамометр до тех пор, пока груз не переместится на 0,25 м. Динамометр при этом будет показывать силу 4,9 Н, но путь, который прошла точка присоединения динамометра, будет равен 0, 5 м. Выполненная работа в этом случае
Проанализировав результаты эксперимента, можно сделать вывод, что использовав подвижный блок, мы получили выигрыш в силе в 2 раза, но проиграли в пути, на котором действовала эта сила, тоже в 2 раза. Работа оказалась одинаковой и в первом, и во втором случае.
Итак, поднимать груз при помощи подвижного блока легче, чем без него. Однако путь, на котором действует сила, будет соответственно большим.
Никакого выигрыша в работе блок не дал. Подобное явление можно наблюдать и при использовании рычага и наклонной плоскости. Такая закономерность была замечена учеными еще в античные времена и выражена в «золотом правиле» механики.
«Золотое правило» механики — это когда ни один простой механизм не дает выигрыша в работе. Если выигрываем в силе, то проигрываем в расстоянии.
При использовании простых механизмов оказывается, что при этом имеется даже некоторый проигрыш в работе. Так, выполняя работу с помощью простого механизма, нужно перемещать еще блок или рычаг, имеющих определенный вес, преодолевать силы трения. Эту работу нельзя назвать полезной.
Как оценить качество простого механизма
Чтобы оценить качество какого-либо простого механизма, сравнивают полезную работу, которую необходимо выполнить без этого механизма, с работой, которая выполняется с использованием простого механизма.
Число, показывающее, какую часть от всей выполненной работы 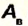
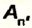
В формулах КПД обозначают греческой буквой 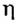
Коэффициент полезного действия удобно выражать в процентах. Тогда
Коэффициент полезного действия может иметь различные значения. Чем его значение больше, тем лучшим считается механизм. Но ни один исследователь или инженер не смог бы изготовить механизм с КПД большим или равным 100 %. И это не из-за несовершенства технологий. Просто этому мешают законы природы, которые человек не в силах изменить.
Таким образом, чтобы оценить качество механизма, необходимо сравнить выполненную и полезную работу.
- Заказать решение задач по физике
Пример задачи с решением
С помощью подвижного блока массой 2 кг на высоту 5 м подняли груз массой 20 кг. Определить коэффициент полезного действия установки.
Дано:
Решение
По определению
Полезная работа
Выполненная работа
Ответ.
- Потенциальная энергия
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
- Работа, мощность и энергия
- Энергия в физике
- Мощность в физике
- Взаимодействие тел
- Механическая энергия и работа
Простые механизмы. «Золотое правило» механики
- Виды простых механизмов
- Принцип действия рычага
- «Золотое правило» механики
- Блоки и полиспасты
- «Золотое правило» механики для гидравлического пресса
- «Золотое правило» механики для наклонной плоскости
- Задачи
п.1. Виды простых механизмов
Простой механизм – это механическое устройство, изменяющее направление или величину силы.
По традиции, сложившейся ещё со времен Возрождения, к простым механизмам относятся:
- наклонная плоскость и её разновидности – клин и винт;
- рычаг и его разновидности – блок и ворот;
- колесо;
- поршень.
Примеры физических систем в механике
п.2. Принцип действия рычага
Подробно рычаги и условия равновесия были рассмотрены в §26 данного справочника.
Там же было получено правило моментов $$ F_1L_1=F_2L_2. $$
Если (F_2) – это нагрузка, а (F_1) — приложенная сила, то выигрыш в силе: $$ i=frac{F_2}{F_1}=frac{L_1}{L_2} $$
В этом разделе мы рассмотрим принцип работы рычага с точки зрения закона сохранения энергии.
Пусть действие приложенной силы (F_1) приводит к перемещению (h_1) левого плеча вниз.
Работа приложенной силы равна (A_1=F_1h_1).
Тогда правое плечо при этом переместится вверх на расстояние (h_2).
Работа нагрузки (A_2=-F_2h_2). Работа нагрузки отрицательна, т.к. направления вектора нагрузки (F_2) и вектора перемещения (h_2) противоположны. Для замкнутой системы выполняется закон сохранения энергии, а значит, сумма работ должна быть равна нулю: $$ A_1+A_2=F_1h_1-F_2h_2=0 $$
Получаем, что (F_1h_1=F_2h_2).
Равнобедренный треугольник с основанием (h_1) и боковыми сторонами (L_1) слева подобен равнобедренному треугольнику с основанием (h_2) и боковыми сторонами (L_2) справа (по двум пропорциональным сторонам и углу между ними). Следовательно, выигрыш в силе: $$ i=frac{F_2}{F_1}=frac{h_1}{h_2}=frac{L_1}{L_2} $$
Что соответствует результату, полученному ранее.
п.3. «Золотое правило» механики
«Золотое правило» механики
Ни один механизм не дает выигрыша в работе.
Во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии.
Выигрыш в силе для рычага $$ i=frac{F_2}{F_1}=frac{h_1}{h_2} $$ показывает, что перемещение (h_1) левого плеча с приложенной силой (F_1) обязательно должно быть в разы больше перемещения (h_2) правого плеча с нагрузкой.
 |
Архимеду приписывают следующую фразу: «Дайте мне точку опоры, и я переверну Землю». Попробуем для начала хотя бы сдвинуть Землю на 1 микрон с орбиты, (h_2=1 text{мкм}=10^{-6} text{м}). Это послужит хорошей иллюстрацией «золотого ПРАВИЛО» механики. |
Допустим, мы нашли «точку опоры» и можем приложить к рычагу силу, равную собственному весу (F_1=720 text{Н}). Сила, удерживающая Землю на орбите вокруг Солнца равна (F_2=3,6cdot 10^{22} text{Н}). Получаем, что нам нужно со своей стороны переместить рычаг на $$ h_1frac{F_2}{F_1}h_2=frac{3,6cdot 10^{22}}{720}cdot 10^{-6}=5cdot 10^{13} (text{м})=5cdot 10^{10} (text{км}) $$ т.е. 50 миллиардов километров.
Расстояние от Солнца до Земли – 1 астрономическая единица – это «всего лишь» 150 миллионов километров:(1 text{а.е.}approx 1,5cdot 10^{11} text{(м)}).
Радиус всей Солнечной системы – около 100 астрономических единиц, т.е. около (1,5cdot 10^{13} text{м}). Тогда (5cdot 10^{13} text{м}) — это чуть больше полутора диаметров Солнечных систем.
Значит, если на одной стороне рычага мы сдвигаем Землю на 1 микрон, то на другой стороне – прикладывая весь свой вес – должны преодолеть расстояние в полторы Солнечных системы. Вот что такое – «проигрыш в расстоянии».
п.4. Блоки и полиспасты
Блок — это колесо с желобом, по которому пропущена веревка или трос.
В технике используют неподвижные и подвижные блоки.
 |
Неподвижный блок Ось неподвижного блока закреплена и при подъёме грузов неподвижна. Неподвижный блок – равноплечий рычаг с точкой вращения (O). Получаем тождество $$ FR=FR $$ где (R) — радиус блока. Выигрыша в силе нет. Неподвижный блок позволяет менять направление действия силы, но выигрыша в силе не даёт. Зато нет и проигрыша в расстоянии: на какое расстояние опустится веревка справа, на такое же расстояние поднимется груз слева. |
 |
Подвижный блок Ось подвижного блока поднимается или опускается вместе с грузом. По правилу моментов для рычага с точкой вращения (O) получаем тождество: $$ Fcdot OA=frac F2cdot OB Leftrightarrow Fcdot R=frac F2cdot 2R $$ Откуда следует двойной выигрыш в силе. Подвижный блок даёт выигрыш в силе в 2 раза. |
В реальных ситуациях выигрыш в силе при использовании подвижного блока получается меньшим, т.к. часть работы уходит на подъем самой веревки и блока (они тоже имеют вес) и преодоление трения.
На практике используют комбинации из неподвижных и подвижных блоков – полиспасты.
Они позволяют получить выигрыш в силе и менять её направление.
Чем больше в полиспасте подвижных блоков, тем большим будет выигрыш в силе.
Характеристики полиспастов представлены в таблице.
| № | К-во неподвижных блоков | К-во подвижных блоков | Изменение направления силы, раз | Выигрыш в силе, раз | Проигрыш в расстоянии, раз |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 2 | 2 |
| 3 | 1 | 2 | 1 | 3 | 3 |
| 4 | 1 | 3 | 1 | 4 | 4 |
| 5 | 1 | 4 | 1 | 5 | 5 |
| 6 | 1 | 5 | 1 | 6 | 6 |
п.5. «Золотое правило» механики для гидравлического пресса
Подробней о гидравлическом прессе – см. §30 данного справочника.
 |
Когда малый поршень под действием силы (F_1), опускается вниз на расстояние (h_1), он вытесняет некоторый объём жидкости. На столько же увеличивается объём жидкости под большим поршнем, который при этом поднимается на высоту (h_2). При опускании малого поршня слева сила (F_1) совершает работу (A_1=F_1h_1), где (h_1) — длина хода. При этом из левого сосуда в правый вытесняется объем воды $$ V=S_1h_1=S_2h_2 $$ |
В правом сосуде при подъёме поршня совершается работа $$ A_2=F_2h_2. $$
Давление на одном уровне в обоих сообщающихся сосудах равно $$ p=frac{F_1}{S_1}=frac{F_2}{S_2}. $$
Получаем: $$ left. begin{array}{r} p=frac{F_1}{S_1}=frac{F_2}{S_2}Rightarrow frac{S_2}{S_1}=frac{F_2}{F_1}\ V=S_1h_1=S_2h_2Rightarrow frac{S_2}{S_1}=frac{h_1}{h_2} end{array} right} Rightarrow frac{F_2}{F_1}=frac{h_1}{h_2}Rightarrow F_1h_1=F_2h_2Rightarrow A_1=A_2 $$
Работы малого и большого поршня равны.
Таким образом, «золотое правило» для гидравлического пресса также выполняется.
Гидравлический пресс не дает выигрыша в работе.
Выигрыш в силе равен проигрышу в расстоянии: $$ i=frac{F_2}{F_1}=frac{h_1}{h_2} $$
п.6. «Золотое правило» механики для наклонной плоскости
Если груз поднимать равномерно вертикально вверх на высоту (h) (из точки C в точку B), необходимо прикладывать силу, равную весу (P). При этом работа по подъему груза равна произведению веса на высоту: $$ A_{CB}=Ph $$
Если груз поднимать равномерно по наклонной плоскости вверх на высоту (h) (из точки A в точку B), работа по подъему груза равна произведению приложенной силы на длину: $$ A_{AB}=FL $$
В любом случае тело, оказавшись в точке B, приобретает потенциальную энергию begin{gather*} E_p=mgh,\[7pt] Delta E_p=E_p-E_{p0}=mgh-0=mgh end{gather*}
Работа внешних сил при этом $$ A_{CB}=A_{AB}=Delta E_p $$
Получаем begin{gather*} Ph=FL\[7pt] i=frac PF=frac Lh end{gather*}
Наклонная плоскость не дает выигрыша в работе.
Выигрыш в силе компенсируется проигрышем в расстоянии.
Выигрыш в силе равен отношению длины наклонной плоскости к высоте.
Например, из пяти наклонных плоскостей, представленных на рисунке, наибольший выигрыш в силе даст плоскость 5, т.к. у нее отношение (frac Lh) максимально (угол наклона минимален).
В реальности, если учесть силу трения, этот выигрыш уменьшается, т.к. с уменьшением угла наклона сила трения растет.
п.7. Задачи
Задача 1. Груз весом 200 Н равномерно поднимают по наклонной плоскости на высоту 5 м, прикладывая силу 100 Н. Найдите длину наклонной плоскости. Трением можно пренебречь.
Дано:
(P=200 text{Н})
(h=5 text{м})
(F=100 text{Н})
__________________
(L-?)
Работы при подъеме тела вверх и при перемещении вдоль наклонной плоскости равны: (A=Ph=FL). Получаем begin{gather*} L=frac PF h end{gather*} Подставляем begin{gather*} L=frac{200}{100}cdot 5=10 (text{м}) end{gather*} Ответ: 10 м
Задача 2. При штамповке детали больший поршень гидравлического пресса поднялся на 1 см, а меньший поршень опустился на 20 см. Какая сила действовала на деталь, если на малый поршень действовала сила 500 Н.
Дано:
(h_1=20 text{см}=0,2 text{м})
(h_2=1 text{см}=0,01 text{м})
(F_1=500 text{Н})
__________________
(F_2-?)
Работы по перемещению поршней равны: begin{gather*} A=F_1h_1=F_2h_2 end{gather*} Сила, действующая на деталь begin{gather*} F_2=frac{h_1}{h_2}F_1,\[6pt] F_2=frac{0,2}{0,01}cdot 500=10000 (text{Н})=10 (text{кН}) end{gather*} Ответ: 10 кН
Задача 3. К концам рычага длиной 1 м подвешены грузы массой 8 кг и 12 кг. На каком расстоянии от середины рычага должна быть точка опоры, чтобы рычаг находился в равновесии? Ответ запишите в сантиметрах.
Дано:
(m_1=8 text{кг})
(m_2=12 text{кг})
(d=1 text{м})
__________________
(x-?)
Плечо для груза 1: begin{gather*} L_1=frac d2+x end{gather*} Плечо для груза 2: begin{gather*} L_2=frac d2-x end{gather*} Условие равновесия: begin{gather*} F_1L_1=F_2L_2\[6pt] F_1left(frac d2+xright)=F_2left(frac d2-xright)\[6pt] (F_1+F_2)x=(F_2-F_1)frac d2 end{gather*} Учитывая, что (F_1=m_1g) и (F_2=m_2g): begin{gather*} x=left(frac{m_2-m_1}{m_1+m_2}right)frac d2 end{gather*} Получаем begin{gather*} x=left(frac{12-8}{8+12}right)cdot frac 12=frac 15cdot frac 12=0,1 (text{м})=10 (text{см}) end{gather*} Ответ: 10 см
Задача 4. Если груз лежит на левой чашке неравноплечих весов, его уравновешивают гири массой (m_1=2 text{кг}) на правой чашке. Если же груз положить на правую чашку, его уравновесит только одна гиря массой (m_2=0,5 text{кг}) на левой чашке. Какова масса (m) груза? Во сколько раз одно плечо весов длиннее другого?
Пусть длина правого плеча (L_1), левого плеча – (L_2).
По условию задачи begin{gather*} left{ begin{array}{l} mL_1=m_1L_2\ m_2L_1=mL_2 end{array} right. end{gather*} Разделим верхнее равенство на нижнее begin{gather*} frac{mL_1}{m_2L_1}=frac{m_1L_2}{mL_2}Rightarrow frac{m}{m_2}=frac{m_1}{m}Rightarrow m^2=m_1m_2 end{gather*} Масса груза begin{gather*} m=sqrt{m_1m_2}\[7pt] m=sqrt{2cdot 0,5}=1 text{кг} end{gather*} Отношение плечей begin{gather*} frac{L_1}{L_2}=frac{m_1}{m}=frac 21=2 end{gather*} Левое плечо длиннее правого в 2 раза.
Ответ: 1 кг; левое плечо длиннее правого в 2 раза
Задача 5*. Прямолинейный кусок проволоки массой (m=40 text{г}) подвешен за середину. Левую половину куска согнули, как показано на рисунке. Какой массы груз надо подвесить в точке A, чтобы восстановить равновесие.
Пусть длина всей проволоки (L).
Тогда расстояние от центра тяжести проволоки слева до точки подвеса (OK=L/4), а расстояние от центра тяжести проволоки справа до точки подвеса (OE=L/2).
Груз массой (M) подвешен на расстоянии (OA=L/2).
Из ПРАВИЛА моментов получаем: begin{gather*} Mgcdotfrac L2+frac{mg}{2}cdot frac L4=frac{mg}{2}cdot frac L2 end{gather*} Справа в равенстве – моменты, поворачивающие проволоку вокруг точки подвеса O против часовой стрелки, слева – по часовой стрелке.
Сокращаем на (gL) begin{gather*} frac M2+frac m8=frac m4Rightarrow frac m4-frac m8=frac m8Rightarrow M=frac m4\[6pt] M=frac{40}{4}=10 (text{г}) end{gather*} Ответ: 10 г
Задача 6*. Балка массой 1200 кг и длиной 3 м лежит на опорах, равноудаленных от ее концов. Расстояние между опорами 2 м.
Какую силу, перпендикулярную балке и направленную вертикально вверх нужно приложить, чтобы приподнять балку за один из её краёв?
Дано:
(M=1200 text{кг})
(CD=3 text{м})
(AB=2 text{м})
(gapprox 10 text{м/с}^2)
__________________
(F-?)
По условию begin{gather*} AC=BD=frac 12(CD-AB)=frac 12(3-2)=0,5 text{м} end{gather*} Если приподнять балку за левый край с силой (F), то останется только одна опора (B). Балка превращается в рычаг с осью вращения, проходящей через точку (B). Точка (K) — центр тяжести отрезка балки (CB).
Точка (E) — центр тяжести отрезка балки (BD).
По правилу моментов begin{gather*} Fcdot CB+m_2gcdot BE=m_1gcdot KB end{gather*} Слева – моменты, поворачивающие балку вокруг точки (B) по часовой стрелке, справа – против часовой стрелки.
Искомая сила: begin{gather*} F=frac{m_1gcdot KB-m_2gcdot BE}{CB} end{gather*} Плечи сил: begin{gather*} CB=CD-BD=3-0,5=2,5 text{м}\[6pt] KB=frac 12 CB=1,25 text{м}\[6pt] BE=frac 12 BD=0,25 text{м} end{gather*} Распределение масс: begin{gather*} m_1+m_2=M\[6pt] frac{m_1}{m_2}=frac{CB}{BD}=frac{2,5}{0,5}=5Rightarrow 1+5=6 text{частей}\[6pt] m_1=frac 56 M=frac 56cdot 1200=1000 text{кг},\[6pt] m_2=frac 16 M=frac 16cdot 1200=200 text{кг} end{gather*} Подставляем: begin{gather*} F=frac{1000cdot 10cdot 1,25-200cdot 10cdot 0,25}{2,5}=frac{12500-500}{2,5}=4800 (text{Н})=4,8 (text{кН}) end{gather*} Ответ: 4,8 кН