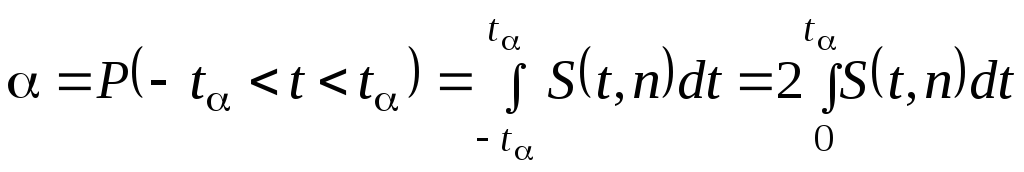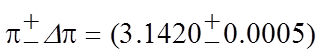Как найти максимальную погрешность при - Avtoru.top

Максимальная погрешность

При оценке результатов измерений иногда
пользуются понятием максимальнойилипредельной допустимой погрешности,
величину которой определяют в доляхилиS. В настоящее
время существуют разные критерии
установления максимальной погрешности,
т.е. границы поля допуска ±,
в котором случайные погрешности должны
уложиться. Пока общепринятым является
определение максимальной погрешности,
равной = 3(или 3S). В последнее
время на основании информационной
теории измерений проф. П.В. Новицкий
рекомендует пользоваться величиной = 2.

Доверительные вероятности и интервал

При оценке погрешностей результатов
измерения требуется определить точность
и надежность полученных результатов
для среднего значения и среднего
квадратичного отклонения. Пусть означает вероятность того, что результат
измерений отличается от истинного
значения на величину, не большую чем.
Это можно записать в виде

. (14)

Вероятность называетсякоэффициентом надежностиилидоверительнойвероятностью,
а интервал значений отдо–доверительным интервалом.

Из выражения (14) следует, что результат
измерений не выходит за пределы
доверительного интервала с вероятностью,
равной , т.е. чем
больше доверительный интервал, тем
вероятнее, что результаты измерения не
выйдут за его пределы и надежность будет
выше. Очевидно, что при этом будет больше
допустимая погрешность (точность
измерения уменьшается). Следовательно,
для характеристики величины случайной
погрешности необходимо задавать два
значения – величину погрешности
(доверительный интервал) и величину
доверительной вероятности, так как
указание только величины погрешности
делает задачу неопределенной. Знание
доверительной вероятности позволяет
оценить степень надежности полученного
результата.

На практике степень надежности проводимых
измерений зависит от их характера. При
большинстве обычных измерений можно
ограничиться доверительной вероятностью
0,9 или 0,95, если не требуется более высокая
степень надежности. Вероятность
определяется законом распределения
погрешностей. Для нормального закона
распределения значение доверительной
вероятности можно определять по (7) или
по таблице прил. 3. Так, например,
средней квадратичной ошибке соответствует значение доверительной
вероятности 0,683; ошибке 2– 0,954; ошибке 3–
0,997.

Ошибки конечного ряда измерений

До настоящего времени искомая величина
А определялась большим числом
измерений (n 17),
и при этом считалось, что она лежит в
некотором интервале.При технических измерениях неизвестная
величина находится при малом числе
измерений(п2),
поэтому следует вводить коэффициентt_на количество измерений

или.

Закон изменения коэффициента t_определяется распределением Стьюдента
(псевдоним английского статистика
Госсета).Распределением Стьюдентапри любомп  2
называется распределение с плотностью
вероятностиS(t, п):

где п
– число измерений;Г– гамма-функция;– нормированное значение случайной
величины.

Для любого заданного значения t_доверительную вероятность (надежность)
неравенстваопределяют с помощью интеграла:

или по
таблице прил. 4.

Значения определяются
из выражения

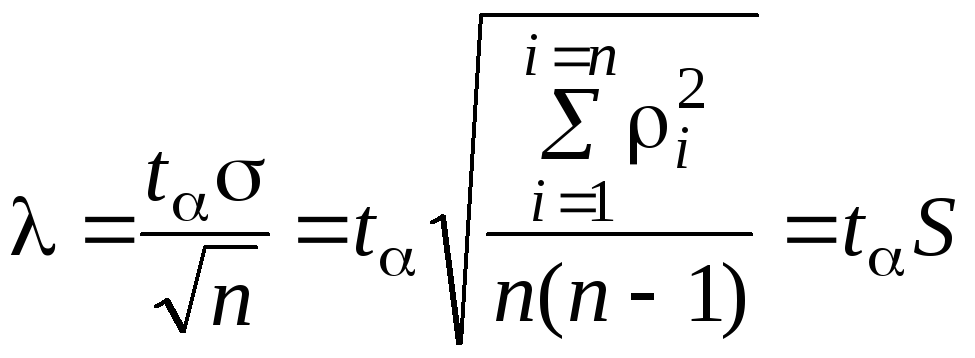
Точность, величина надежности и число
измерений связаны между собой. Зависимость
относительной ошибки от числа измерений
при заданной надежности показана в
табл. 2.

Таблица
2

Относительная	Число измерений п при величине надежности 
ошибка	0,5	0,7	0,8	0,9	0,95	0,99	0,999
1,0	2	3	4	5	7	11	17
0,5	3	6	9	13	18	31	50
0,3	6	13	20	32	46	78	127
0,2	13	29	43	70	99	171	277
0,1	47	109	166	273	387	668	1089

Как показывают расчеты, при
малом числе измерений п
и заданной погрешности
метод Стьюдента дает меньшую надежность,
чем при нормальном законе распределения;
при
распределение Стьюдента приближается
к нормальному.

Соседние файлы в папке Спецгл. ч.2

Источник

Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».

Сначала надо вспомнить основные понятия теории погрешности.

Абсолютная погрешность физической величины ΔА — это
разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:

ΔА = А — А_пр .

Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной
погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.

Относительная погрешность измерения
ε_Аравна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из
множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.

Зная относительную погрешность, найти абсолютную погрешность измерений можно так:

ΔА = ε_A· А.

«Правило ничтожных погрешностей»

при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟4 от другого.

Запись результата с указанием погрешности.

Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.

Пример:

Результат записывается в виде:

А = А_изм ± ΔА, например: ℓ = (13 ± 2) мм.

При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении
погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения). Значение величины и погрешность следует
выражать в одних и тех же единицах!

Пример:

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения

Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?

Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за
топливо?

Источник

Введение

Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B, C, … — физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_иA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)

Δ_оA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔA=Δ_иA + Δ_оA

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае A_пр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется, как показано в таблице 1.

Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A_прε (ε выражается десятичной дробью).

Таблица 1

Формулы для нахождения относительной погрешности косвенных измерений

Nº п/п	Формула физической величины	Формула относительной погрешности
1
2
3	A=B+C
4

2. О классе точности электроизмерительных приборов

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иA от всей шкалы прибора (A_max):

Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (A_max), определяют абсолютную погрешность Δ_иA измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений

1. Записать результаты измерений в виде двойных неравенств:

A_{1 пр} – ΔA₁ < A_{1 пр} < A_{1 пр} + ΔA₁
A_{2 пр} – ΔA₂ < A_{2 пр} < A_{2 пр} + ΔA₂
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.

Рисунок 1.

4. Как оформлять отчет о проделанной работе

Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».

Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.

Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.

домашней странице BARSIC

Расчёт ошибок косвенных измерений

Пусть искомая
величина Апри выбранном
методе косвенных измерений рассчитывается
по формуле:

A
= f(x₁
,x₂
,x₃
,…,x_n
) (12)

где x₁,x₂,…,x_n
— величины, найденные в результате прямых
измерений, с учётом ошибок о которых
шла речь выше. Из-за этих ошибок величина
«А»
так же будет определяться с ошибками.

Пусть X₁,X₂,…,X_N
— значения f(x₁
,x₂
,x₃
,…,x_n), вычисленные
для разных серий измерений (x₁,x₂,…,x_n).

Таблица 1

Таблица коэффициентов
Стьюдента

Число измерений	Доверительная вероятность
0.7	0.8	0.9	0.95	0.99	0.999
2	2.0	3.1	6.3	12.7	63.7	636.6
3	1.3	1.9	2.9	4.3	9.9	31.6
4	1.3	1.6	2.4	3.2	5.8	12.9
5	1.2	1.5	2.1	2.8	4.6	8.6
10	1.1	1.4	1.8	2.3	3.3	4.8
15	1.1	1.3	1.8	2.1	3.0	4.1
20	1.1	1.3	1.7	2.1	2.9	3.9

Абсолютной ошибкой
косвенных измерений, по аналогии с
абсолютной ошибкой прямых измерений,
называют разность между истинным
значением «А» и её значениями,
полученными в результате измерений:

(13)

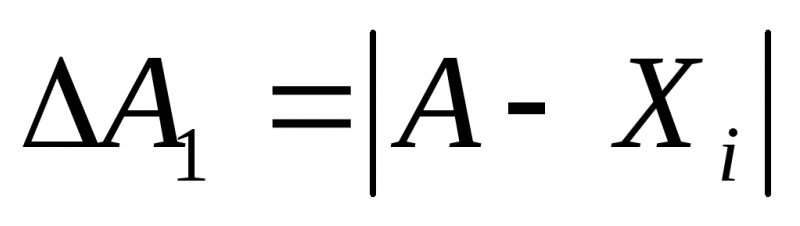
Размерность
абсолютной ошибки совпадает с размерностью
определяемой величины. Относительной
ошибкой косвенных измерений называют
отвлечённое число:

(14)

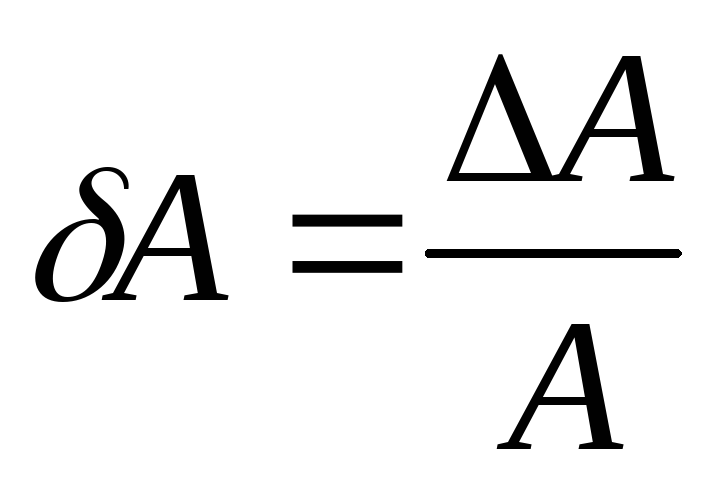
Иногда относительную
ошибку выражают в процентах:

(15)

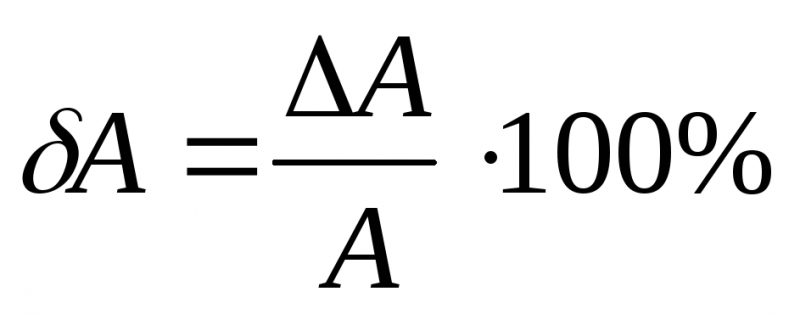
Для определения
величины «А» в формулах (12)…(15) по
теории

вероятностей
следует брать величину Х, которую можно
определить двумя способами:

1) А
= Х
= (Х₁
+ Х₂
+…+Х_n)/n
(16)

2) A
= X
= f(x₁
+ x₂
+…+x_n)
(17)

где x₁,x₂
,…, x_n
определяют по формуле (3). Если ошибки
измерений малы, то оба способа дают
практически тождественные результаты.

Рассмотрим способы
нахождения ошибки величины А,
определённой из косвенных измерений,
по найденным значениям оши

бок прямых измерений.
Выше отмечалось, что возможны различные
соотношения между приборной систематической
и случайными ошибками.

1-й случай. Преобладают
приборные ошибки. В этом случае можно
дать только оценку максимальной ошибки.
Формулы для нахождения предельной
ошибки косвенных измерений по внешнему
виду совпадают с формулами дифференциального
исчисления. В связи с этим для предельной
абсолютной ошибки используется формула:

(18)

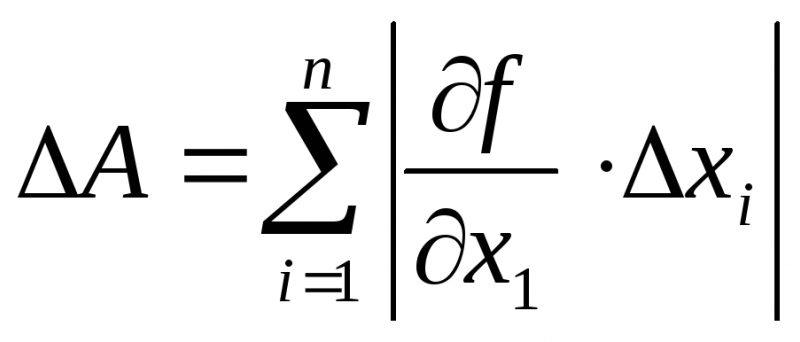
а для расчёта
предельной относительной ошибки пригодна
фор

— 19 —

мула:

(19)

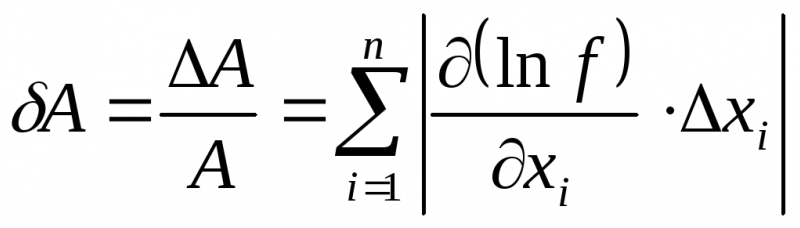
Формулы для расчёта
предельных ошибок некоторых часто
встречающихся функций, когда приборные
ошибки превышают случайные, приведены
в Таблице 2. Эти выражения легко
рассчитываются по формулам (18) и (19).

2-й случай. Преобладают
случайные ошибки. Для определения
среднеквадратичной ошибки теория
вероятностей даёт следующую формулу:

(20)

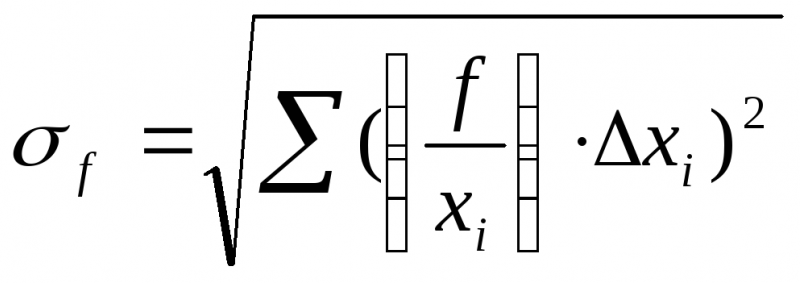
Относительная
ошибка вычисляется по формуле:

(21)

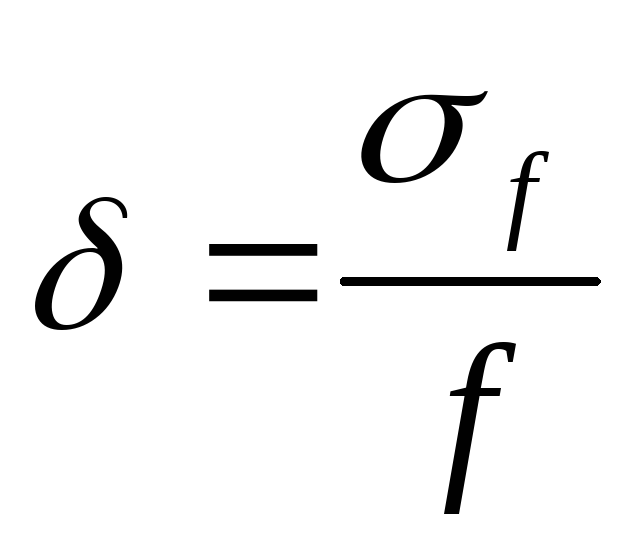
При выполнении
промежуточных расчётов необходимо
помнить, что число точных цифр в результате
расчётов не может увеличиваться. Поэтому
промежуточные результаты округляют,
сохраняя

1…2 избыточных
знака. При этом последующие цифры,
меньшие

5,отбрасываются;если
первая из отбрасываемых цифр больше 5,

то последняя из
оставшихся цифр увеличивается на
единицу. Ес

ли первая
отбрасываемая цифра 5, то предыдущая
цифра остаётся

без изменений,
если она чётная, и увеличивается на
единицу, если

она нечётная.
Выражения для среднеквадратичной ошибки
некоторых часто встречающихся функций
приведены в Таблице 3. Для определения
ошибок косвенных измерений используют
большую из инструментальной или случайной
ошибок прямого измерения.

Методики расчета

Существует несколько методов определения отклонения. Наиболее простой и доступный способ:

Необходимые измерения проводят не менее 5 раз. Это дает возможность вычислить наиболее точное значение параметра. Результаты вносят в таблицу excel.
Полученные величины складывают и делят на количество замеров. В результате получится действительное значение. Его обычно применяют вместо истинного, так как нет возможности вычислить последнее.
Следующий шаг — определение абсолютной погрешности. Ее считают для каждого измерения. Чтобы узнать величину этого показателя, из результата каждого замера вычитают действительное значение

Для обработки данных неважно, положительная или отрицательная получилась цифра. Используют модули полученных чисел, пренебрегая знаками.
Чтобы определить относительную погрешность измерения, нужно разделить абсолютную на действительное значение

Полученное число умножают на 100%.

Для определения предельного отклонения выбирают наибольшее значение из всех полученных.

Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:

Каждый показатель абсолютной погрешности возводят в квадрат и записывают.
Полученные результаты складывают между собой.
Сумму всех квадратов делят на число, которое на единицу меньше количества измерений.
Из результата вычислений извлекают квадратный корень — это и будет среднее квадратическое отклонение.

Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения

Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.

Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение

При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.

При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.

а a изм аист ед.изм. 4

Это
размерная, положительная величина, характеризующая отклонение измеренного от
истинного значений.

Относительная погрешность – это
отношение абсолютной погрешности к истинному значению измеряемой величины.

(5)

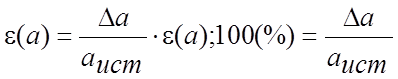
Относительная
погрешность (5) – безразмерная величина, она измеряется в долях или процентах и
показывает какую часть от истинного значения измеряемой величины составляет
погрешность.

На
практике вместо неизвестного истинного значения используют среднее значение
измеряемой величины.

Формула (5) позволяет по
известной одной из характеристик определить другую. Часто вначале удобнее найти
относительную, а через неё абсолютную.

Если
измерение выполнено и погрешности определены, то окончательный результат
записывается в виде

. (6)

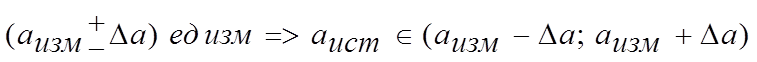
что эквивалентно заданию
интервала, в котором лежит истинное значение искомой величины. И чем уже данный
интервал, тем точнее измерения и наоборот.

4.
Вычисление погрешностей.

За
абсолютную погрешность однократно измеряемой величины применяют приборную
погрешность.

Для
простых измерительных и цифровых приборов приборная погрешностьравная
половине цены деления прибора.

. (7)

Например:
приборная погрешность

миллиметровой линейки (с=1 мм/_дел) равна, Δа_пр
= 0,5 мм.

штангенциркуля (с=0,05 мм/_дел) – Δа_пр
= 0,025 мм.

эл.
секундомера (с=0,001 с/_дел) – Δа_пр
= 0,0005 с.

Для
стрелочных электроизмерительных приборов приборная погрешность определятся
через класс точности прибора (характеристика прибора указанная на его
шкале).

,
(8)

представляющая
собой отношение приборной погрешности к максимальному значению измеряемой
прибором величины. Из (8) для приборной погрешности стрелочных
электроизмерительных приборов получаем:

ΔАприб. = 0,01 · К · Аmax
.
                          (9)

Часто
в расчетах приходится использовать физические и математические постоянные,
которые как правило выражаются сложными десятичными дробями

(π=
3.141593… , е = 2.718282… , с = 2.99792… · 108 м/_с

q_e =
1,60219… · 10-19 Kл , m_е=
1.67265… · 10-31к2 и т.д.).

При
использовании постоянных мы вынуждены их округлять т.е. брать приближённые
значения, это также даёт вклад в погрешность. К погрешностям табличных величин
относятся так же как и к приборным.

За
погрешность табличной величины принимают половину единицы последнего разряда
табличной величины, выбранной с заданной точностью.

Например; при определении
плотности тела цилиндрической формы необходимо использовать число π.
Предварительно оговаривается точность расчётов (например вычисления проводят с
точностью до

четырёх значащих цифр).
Тогда используемое число π и погрешность Δπ соответственно будут равны:

π =
3.142, Δπ = 0.0005

и окончательная запись числа
π с погрешностью имеет вид:

б)
Погрешности многократно измеряемых величин.

Погрешности
многократных измерений в рамках линейной теории оцениваются по следующей схеме

Что такое погрешность?

Представьте, что вас отправили в магазин купить сахар, но вот незадача: фасованный в пачках как раз закончился и остался только на развес. Что делать, вы просите продавца тогда отмерить вам ровно килограмм. Продавец взял лопатку, наполнил пакет, положил его на весы, и они выдают значение — 1.000 кг.

Как удачно положили.

Вы рассчитываетесь и счастливым возвращаетесь домой. А теперь представим, что по необыкновенной случайности у вас дома имеются весы, показывающие массу с точностью до миллиграмма. Вы решаете интереса ради перевесить пакет, чтобы посмотреть, действительно ли его масса равна строго килограмму.

И какого же удивление, когда более точные весы показывают массу не в 1.000 кг, а в 0.999990 кг. Иными словами, вас обсчитали. Обсчитали, между прочим, на десять миллиграмм!

Чем меньше цена деления прибора, тем точнее измерение. Ваши весы с учетом массы до миллиграмма оказались точнее магазинных «граммовых» весов. Однако и это не предел, ведь существуют фармакологические весы, определяющие массу до микрограмма — одной миллиардной килограмма. Так можно продолжать до бесконечности, пока у нас не закончатся технологические возможности сконструировать еще более точные весы.

Однако все измерительные приборы, пусть и самые точные, несовершенны. Несовершенно даже само то, как мы видим, слышим и ощущаем мир вокруг. Это, наряду с прочими факторами, приводит к тому, что при измерении величины получается ее приближенное значение, не истинное.

Разница между приближенным и истинным значениями и называется погрешностью.

Важно. Погрешность не равно ошибке

В обычном, бытовом языке мы привыкли к тому, что слово «погрешность» у нас ассоциируется с просчетом или упущением.

В физике погрешность — обыденное явление, присутствующее внутри практически каждой величины, и мало что имеет общего с ошибкой в привычном понимании слова.

Все величины, которые, к примеру, вы видите в типовых физических задачах на вычисление, так или иначе содержат погрешность. Ее не обозначают для удобства. Поэтому помните о невозможности проводить эксперименты в идеальных условиях и о том, что ни один прибор чаще всего не сможет показать результат таким, каков он есть на самом деле.

Как правило, при однократном проведении измерения определить значение погрешности крайне затруднительно: для ее выявления обычно проводят серию равноточных измерений — измерений, произведенных в одинаковых условиях.

После результаты сличаются, то есть сравниваются между собой и, при необходимости, сопоставляются с различными экспериментальными величинами. На основе данных, полученных в результате измерений и сличения, вычисляется погрешность.

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

При многократном измерении одной и той же величины каждый раз получают несколько отличающиеся результаты, как по абсолютной величине, так и по знакам, каким бы опытом не обладал исполнитель и какими бы высокоточными приборами он не пользовался.
Погрешности различают: грубые, систематические и случайные.
Появление грубых погрешностей (промахов) связано с серьезными ошибками при производстве измерительных работ. Эти ошибки легко выявляются и устраняются в результате контроля измерений.Систематические погрешностивходят в каждый результат измерений по строго определенному закону. Они обусловлены влиянием конструкции измерительных приборов, погрешностями градуировки их шкал, износом и т. д. (инструментальные погрешности)иливозникают из-за недоучета условий измерений и закономерностей их изменений, приближенности некоторых формул и др. (методические погрешности). Систематические погрешности делятся на постоянные (неизменные по знаку и вели чине) и переменные (изменяющие свою величину от одного измерения к другому по определенному закону).
Такие погрешности заранее определимы и могут быть сведены к необходимому минимуму путем введения соответствующих поправок.Например, заранее может быть учтено влияние кривизны Земли на точность определения вертикальных расстояний, влияние температуры воздуха и атмосферного давления при определении длин линий светодальномерами или электронными тахеометрами, заранее можно учесть влияние рефракции атмосферы и т. д.
Если не допускать грубых погрешностей и устранять систематические, то качество измерений будет определяться только случайными погрешностями. Эти погрешности неустранимы, однако их поведение подчиняется законам больших чисел. Их можно анализировать, контролировать и сводить к необходимому минимуму.
Для уменьшения влияния случайных погрешностей на результаты измерений прибегают к многократным измерениям, к улучшению условий работы, выбирают более совершенные приборы, методы измерений и осуществляют тщательное их производство.
Сопоставляя ряды случайных погрешностей равноточных измерений можно обнаружить, что они обладают следующими свойствами:
а) для данного вида и условий измерений случайные погрешности не могут превышать по абсолютной величине некоторого предела;
б) малые по абсолютной величине погрешности появляются чаще больших;
в) положительные погрешности появляются так же часто, как и равные им по абсолютной величине отрицательные;
г) среднее арифметическое из случайных погрешностей одной и той же величины стремится к нулю при неограниченном увеличении числа измерений.
Распределение ошибок, соответствующее указанным свойствам, называется нормальным (рис. 12.1).

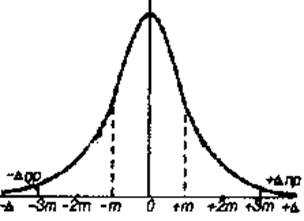
Рис. 12.1. Кривая нормального распределения случайных погрешностей Гаусса

Разность между результатом измерения некоторой величины (l) и ее истинным значением (X) называют абсолютной (истинной) погрешностью.

Δ = l — X

Истинное (абсолютно точное) значение измеряемой величины получить невозможно, даже используя приборы самой высокой точности и самую совершенную методику измерений. Лишь в отдельных случаях может быть известно теоретическое значение величины. Накопление погрешностей приводит к образованию расхождений между результатами измерений и действительными их значениями.Разность суммы практически измеренных (или вычисленных) величин и теоретического ее значения называется невязкой. Например, теоретическая сумма углов в плоском треугольнике равна 180º, а сумма измеренных углов оказалась равной 180º02′; тогда погрешность суммы измеренных углов составит +0º02′. Эта погрешность будет угловой невязкой треугольника.
Абсолютная погрешность не является, полным показателем точности выполненных работ. Например, если некоторая линия, фактическая длина которой составляет 1000 м, измерена землемерной лентой с ошибкой 0,5 м, а отрезок длиною 200 м – с ошибкой 0,2 м, то, несмотря на то, что абсолютная погрешность первого измерения больше второго, все же первое измерение было выполнено с точностью в два раза более высокой. Поэтому вводят понятие относительной погрешности:

Отношение абсолютной погрешности измеряемой величины Δ к измеренной величине l называют относительной погрешностью.

Относительные погрешности всегда выражаются дробью с числителем, равным единице (аликвотная дробь). Так, в приведенном выше примере относительная погрешность первого измерения составляет

а второго

30 Поверка и калибровка си. Определения. Правовые основы.

В
соответствии с законом РК «Об обеспечении
единства измерений» введены следующие
понятия:

— поверка
средства измерений —
совокупность операций, выполняемых
органами Государственной метрологической
службы (другими уполномоченными на то
органами, организациями) с целью
определения и подтверждения соответствия
средства измерений установленным
требованиям;

— калибровка
средств измерений —
совокупность операций, выполняемых с
целью определения и подтверждения
действительных значений метрологических
характеристик и/или пригодности к
применению средства измерений, не
подлежащего государственному
метрологическому контролю и надзору.

В
обоих случаях, как при поверке, так и
при калибровке, определяются метрологические
характеристики средств измерений,
причем часто по одной и той же методике,
называемой методикой
поверки,
но на этом их сходство заканчивается. Различия
между этими понятиями имеют
более принципиальный характер.

Во-первых,
в сферах распространения ГМКиН могут
применяться только поверенные СИ, а
калиброванные — не могут.

Во-вторых,
поверке могут подвергаться только СИ
утвержденного типа, то есть внесенные
в Государственный реестр СИ, а калибровке
— любые, в том числе нестандартизованные
и изготовленные в одном экземпляре.

В-третьих,
при поверке проверяется соответствие
СИ своему типу, внесенному в Государственный
реестр, тогда как при калибровке
определяются действительные
метрологические характеристики, которые
прибор имеет на момент калибровки.

Если
при поверке СИ обнаружено его несоответствие
хотя бы одному пункту утвержденного
типа, средство измерений должно быть
забраковано. При калибровке этому СИ
будут приписаны новые значения
метрологических характеристик.

Положительные
результаты поверки удостоверяются
поверительным клеймом или свидетельством
о поверке. Если средство измерений по
результатам поверки признано непригодным
к применению, оттиск поверительного
клейма и свидетельство о поверке
аннулируются и выписывается извещение
о непригодности или делаются соответствующие
записи в технической документации.

Результаты
калибровки удостоверяются калибровочным
знаком (клеймом), наносимым на средство
измерений, или сертификатом о калибровке,
а также, записью в эксплуатационных
документах. В соответствии с законом
РК «Об обеспечении единства измерений»
калибровка средств измерений является
процедурой добровольной и осуществляемой
по желанию владельца прибора с целью,
например, получения достоверных
результатов измерений, влияющих, в
конечном счете, на результаты труда.
ГМКиН на такие средства измерений не
распространяется.

Абсолютная погрешность — измерительный прибор

Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.

Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.

Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.

Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.

В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.

В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.

Источник

Физические величины и погрешности их измерений — Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение.

При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины,
Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте,

Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений, При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов.

Отсчет по шкале прибора указывает непосредственно измеряемое значение.
Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).

Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины X Д, Действительное значение величины X Д (согласно РМГ 29-99 ) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.

Различают абсолютную (∆ X) и относительную (δ) погрешности измерений.
Абсолютная погрешность измерения – это п огрешность средства измерений, выраженная в единицах измеряемой физической величины, характеризующая абсолютное отклонение измеряемой величины от действительного значения физической величины: ∆X = X – X Д,

Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%, При оценке точности косвенных измерений некоторой величины X 1, функционально связанной с физическими величинами X 2, X 3,, X 1 = F (X 2, X 3, ), учитывают погрешности прямых измерений каждой из величин X 2, X 3, и характер функциональной зависимости F (),

Как вычислить погрешность измерений?

Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).

расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.

Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.

У нас есть два варианта определения длины этого бруска. (1). Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2). Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).

Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.

В чем измеряется погрешность?

Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).

Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Инструментальные и методические погрешности.
Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях.
Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.

Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.

Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.

Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Как найти абсолютную погрешность измерительного прибора?

Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δ и x + Δ о x при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.

Что такое погрешность метода измерений?

По источнику возникновения — Инструментальная погрешность Эта погрешность определяется несовершенством прибора, возникающим, например, из-за неточной калибровки, Методическая погрешность Методической называют погрешность, обусловленную несовершенством метода измерений.

Что такое погрешность измерительного прибора?

Определение — Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.

Как определить погрешность деления?

Как определить погрешность и объем жидкости — Погрешность равна половине цены деления мензурки. В нашем случае погрешность составляет 2,5 мл. Чтобы определить объем, берем ближайшее число от верхней границы жидкости (на рисунке — это значение 40 мл) и прибавляем количество штрихов (на рисунке — 2 штриха) по 5 мл: V = 40 + 2 × 5 = 50 мл.

Как рассчитывается приведенная погрешность?

Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений.

Общие требования» и им подобных.
Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия.
Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п.

Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.

Абсолютная погрешность: Δ = X д — X изм, выражается в единицах измеряемой величины, например в килограммах (кг), при измерении массы. где X д – действительное значение измеряемой величины, принимаются обычно показания эталона, образцового средства измерений; X изм – измеренное значение.
Относительная погрешность: δ = (Δ ⁄ X д ) · 100, выражается в % от действительного значения измеренной величины.
Приведённая погрешность: γ = (Δ ⁄ X н ) · 100, выражается в % от нормирующего значения. где X н – нормирующее значение, выраженное в тех же единицах, что и Δ, обычно принимается диапазон измерения СИ (шкала).

По характеру проявления:

систематические (могут быть исключены из результатов);
случайные;
грубые или промахи (как правило не включаются в результаты измерений).

В зависимости от эксплуатации приборов:

основная – это погрешность средства измерения при нормальных условиях; (ГОСТ 8.395-80)
дополнительная погрешность – это составляющая погрешности средства измерения, дополнительно возникающая из-за отклонения какой-либо из влияющих величин от нормативного значения или выход за пределы нормальной области значений. Например: измерение избыточного давления в рабочих условиях цеха, при температуре окружающего воздуха 40 ºС, относительной влажности воздуха 18% и атмосферном давлении 735 мм рт. ст., что не соответствует номинальным значениям влияющих величин при проведении поверки.

Наимено вание погреш ности

Формула

Форма выражения, записи

Обозначение класса точности

В докумен тации

На сред стве изме рений

Абсолют ная

Δ = X д — X изм

Δ = ±50 мг Примеры: Номинальная масса гири 1 кг ±50 мг Диапазон измерения весов среднего III класса точности от 20 г до 15 кг ±10 г

Класс точности: М 1 Класс точности: средний III Примечание: на многие виды измерений есть свои НД по выражению погрешностей, здесь для примера взято для гирь и весов.

М 1

Относи тельная

δ = (Δ ⁄ X д ) · 100

δ = ±0,5 Пример: Измеренное значение изб.

Как вычислить абсолютную погрешность формула?

Поиск: Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ).

Чему равна абсолютная погрешность?

При измерении каких-либо величин важным понятием является понятие о погрешности. Это связано с тем, что абсолютно точно измерить какую либо величину невозможно. Поэтому вводят понятие погрешности. Есть очень много видов погрешности, связанных с человеческим фактором или процессом измерения.

Для чего нужна погрешность измерений?

Каждое физическое измерение в исследованиях и промышленности сопровождается определенной погрешностью. Даже незначительные колебания в условиях окружающей среды могут влиять на измерение и вызывать отклонения, которые делают результат измерения ненадежным.

Для получения правильных результатов измерений необходимо учитывать связанную с результатами погрешность. Погрешность измерений указывает на недостающую информацию о настоящем значении измеряемой величины. Она определяется параметром, выраженным в процентах и относящимся к результату измерения, который обозначает отклонение значений, которое обоснованно можно присвоить измеряемой величине на основе имеющейся информации.

Другими словами, это диапазон, в пределах которого с определенной вероятностью находится истинное значение измеряемой величины.

Как найти абсолютную погрешность пример?

Абсолютная погрешность — Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример : в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26. Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности.
Обозначим точное число буквой А, а буквой а – приближение к точному числу.
Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях.
Тогда формула будет выглядеть следующим образом: Δа=А-а.
Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой.

Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения. Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см.

Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Как определить цену деления и погрешность?

Найти две соседних отметки шкалы, возле которых написаны величины, соответствующие этим отметкам шкалы; найти разность этих величин; сосчитать количество промежутков между величинами отметок шкалы; полученную разность величин разделить на количество промежутков.

Что такое максимальная погрешность измерений?

Предельная погрешность измерения в ряду измерений – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.

Как рассчитывается приведенная погрешность?

Общие требования» и им подобных. Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия. Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п.

Абсолютная погрешность: Δ = X д — X изм, выражается в единицах измеряемой величины, например в килограммах (кг), при измерении массы. где X д – действительное значение измеряемой величины, принимаются обычно показания эталона, образцового средства измерений; X изм – измеренное значение.
Относительная погрешность: δ = (Δ ⁄ X д ) · 100, выражается в % от действительного значения измеренной величины.
Приведённая погрешность: γ = (Δ ⁄ X н ) · 100, выражается в % от нормирующего значения. где X н – нормирующее значение, выраженное в тех же единицах, что и Δ, обычно принимается диапазон измерения СИ (шкала).

По характеру проявления:

систематические (могут быть исключены из результатов);
случайные;
грубые или промахи (как правило не включаются в результаты измерений).

В зависимости от эксплуатации приборов:

основная – это погрешность средства измерения при нормальных условиях; (ГОСТ 8.395-80)
дополнительная погрешность – это составляющая погрешности средства измерения, дополнительно возникающая из-за отклонения какой-либо из влияющих величин от нормативного значения или выход за пределы нормальной области значений. Например: измерение избыточного давления в рабочих условиях цеха, при температуре окружающего воздуха 40 ºС, относительной влажности воздуха 18% и атмосферном давлении 735 мм рт. ст., что не соответствует номинальным значениям влияющих величин при проведении поверки.

Наимено вание погреш ности

Формула

Форма выражения, записи

Обозначение класса точности

В докумен тации

На сред стве изме рений

Абсолют ная

Δ = X д — X изм

М 1

Относи тельная

δ = (Δ ⁄ X д ) · 100

δ = ±0,5 Пример: Измеренное значение изб.

Как вычислить погрешность функции?

Главная страница УЧЕБНЫЕ МАТЕРИАЛЫ ПРОГРАММА КУРСА КОНСПЕКТЫ ЛЕКЦИЙ ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ВОПРОСЫ К ЗАЧЁТУ РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Кафедра физхимии ЮФУ (РГУ) ЧИСЛЕННЫЕ МЕТОДЫ И ПРОГРАММИРОВАНИЕ Материалы к лекционному курсу Лектор – Щербаков И.Н. Пусть X – некоторая величина, истинное значение которой известно или неизвестно и равно x*, Число x, которое можно принять за значение величины X, мы будем называть ее приближенным значением или просто приближенным числом. Число x называют приближенным значением по недостатку, если оно меньше истинного значения ( x < x* ), и по избытку, если оно больше ( x > x* ). Например, число 3,14 является приближенным значением числа π по недостатку, а 2,72 – приближенным значением числа е (основание натурального логарифма) по избытку. Абсолютная погрешность приближенного числа есть абсолютная величина разности между истинным значением величины и данным ее приближенным значением. Δx = | x * – x | Поскольку истинное значение величины обычно остается неизвестным, неизвестной остается также и абсолютная погрешность. Вместо нее приходится рассматривать оценку абсолютной погрешности, так называемою предельную абсолютную погрешность, которая означает число, не меньшее абсолютной погрешности (далее, в том случае, если это не принципиально, будем под абсолютной погрешностью понимать именно предельную абсолютную погрешность). Абсолютная погрешность приближенного числа не в полной мере характеризует его точность. Действительно, погрешность в 0,1 г слишком велика при взвешивании реактивов для проведения микро-синтеза, допустима при взвешивании 100 г колбасы, и не может быть замечена при измерении массы, например, железнодорожного вагона. Более информативным показателем точности приближенного числа является его относительная погрешность, Относительной погрешностью δx приближенного значения величины X называют абсолютную величину отношения его абсолютной погрешности к истинному значению этой величины. Часто эту относительную погрешность выражают в процентах. C учетом положительности абсолютной погрешности можно записать: δx = Δx / | x* | Ввиду того, что фактически вместо абсолютной погрешности приходится рассматривать предельную, относительную погрешность также заменяют предельной относительной погрешностью, которая означает число, не меньшее относительной погрешности. Более того, при отыскании предельной относительной погрешности приходится заменять неизвестное истинное значение величины x* приближенным – x, Последняя замена обычно не отражается на величине относительной погрешности ввиду близости этих значений и малости абсолютной погрешности. δx = Δx / | x | Например, для приближенного значения π = 3,14 предельная абсолютная погрешность составляет 0,0016, а относительная – 0,00051 или 0,051%. Выражение относительной погрешности в процентах иногда называют процентной погрешностью.

Как рассчитать абсолютную погрешность?

Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ).

Adblock
detector

Источник

From Wikipedia, the free encyclopedia

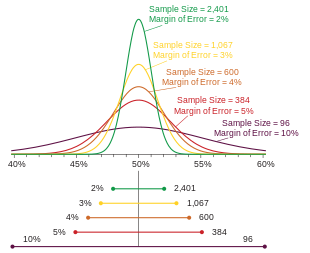
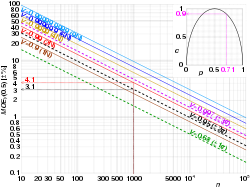
Probability densities of polls of different sizes, each color-coded to its 95% confidence interval (below), margin of error (left), and sample size (right). Each interval reflects the range within which one may have 95% confidence that the true percentage may be found, given a reported percentage of 50%. The margin of error is half the confidence interval (also, the radius of the interval). The larger the sample, the smaller the margin of error. Also, the further from 50% the reported percentage, the smaller the margin of error.

The margin of error is a statistic expressing the amount of random sampling error in the results of a survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a census of the entire population. The margin of error will be positive whenever a population is incompletely sampled and the outcome measure has positive variance, which is to say, whenever the measure varies.

The term margin of error is often used in non-survey contexts to indicate observational error in reporting measured quantities.

Concept[edit]

Consider a simple yes/no poll as a sample of respondents drawn from a population reporting the percentage of yes responses. We would like to know how close is to the true result of a survey of the entire population , without having to conduct one. If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), we would expect those subsequent results ${displaystyle p_{1},p_{2},ldots }$ to be normally distributed about . The margin of error describes the distance within which a specified percentage of these results is expected to vary from .

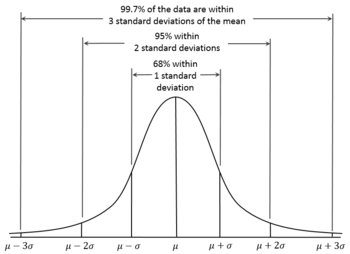
According to the 68-95-99.7 rule, we would expect that 95% of the results ${displaystyle p_{1},p_{2},ldots }$ will fall within about two standard deviations ( ${displaystyle pm 2sigma _{P}}$ ) either side of the true mean . This interval is called the confidence interval, and the radius (half the interval) is called the margin of error, corresponding to a 95% confidence level.

Generally, at a confidence level gamma , a sample sized of a population having expected standard deviation sigma has a margin of error

${displaystyle MOE_{gamma }=z_{gamma }times {sqrt {frac {sigma ^{2}}{n}}}}$

where ${displaystyle z_{gamma }}$ denotes the quantile (also, commonly, a z-score), and ${displaystyle {sqrt {frac {sigma ^{2}}{n}}}}$ is the standard error.

Standard deviation and standard error[edit]

We would expect the average of normally distributed values ${displaystyle p_{1},p_{2},ldots }$ to have a standard deviation which somehow varies with . The smaller , the wider the margin. This is called the standard error ${displaystyle sigma _{overline {p}}}$ .

For the single result from our survey, we assume that , and that all subsequent results ${displaystyle p_{1},p_{2},ldots }$ together would have a variance ${displaystyle sigma _{P}^{2}=P(1-P)}$ .

${displaystyle {text{Standard error}}=sigma _{overline {p}}approx {sqrt {frac {sigma _{P}^{2}}{n}}}approx {sqrt {frac {p(1-p)}{n}}}}$

Note that corresponds to the variance of a Bernoulli distribution.

Maximum margin of error at different confidence levels[edit]

For a confidence level gamma , there is a corresponding confidence interval about the mean ${displaystyle mu pm z_{gamma }sigma }$ , that is, the interval ${displaystyle [mu -z_{gamma }sigma ,mu +z_{gamma }sigma ]}$ within which values of should fall with probability gamma . Precise values of ${displaystyle z_{gamma }}$ are given by the quantile function of the normal distribution (which the 68-95-99.7 rule approximates).

Note that ${displaystyle z_{gamma }}$ is undefined for , that is, ${displaystyle z_{1.00}}$ is undefined, as is ${displaystyle z_{1.10}}$ .

	${displaystyle z_{gamma }}$			${displaystyle z_{gamma }}$
0.68	0.994457883210	0.999	3.290526731492
0.90	1.644853626951	0.9999	3.890591886413
0.95	1.959963984540	0.99999	4.417173413469
0.98	2.326347874041	0.999999	4.891638475699
0.99	2.575829303549	0.9999999	5.326723886384
0.995	2.807033768344	0.99999999	5.730728868236
0.997	2.967737925342	0.999999999	6.109410204869

Since ${displaystyle max sigma _{P}^{2}=max P(1-P)=0.25}$ at p=0.5 , we can arbitrarily set , calculate ${displaystyle sigma _{P}}$ , ${displaystyle sigma _{overline {p}}}$ , and ${displaystyle z_{gamma }sigma _{overline {p}}}$ to obtain the maximum margin of error for at a given confidence level gamma and sample size , even before having actual results. With

${displaystyle MOE_{95}(0.5)=z_{0.95}sigma _{overline {p}}approx z_{0.95}{sqrt {frac {sigma _{P}^{2}}{n}}}=1.96{sqrt {frac {.25}{n}}}=0.98/{sqrt {n}}=pm 3.1%}$

${displaystyle MOE_{99}(0.5)=z_{0.99}sigma _{overline {p}}approx z_{0.99}{sqrt {frac {sigma _{P}^{2}}{n}}}=2.58{sqrt {frac {.25}{n}}}=1.29/{sqrt {n}}=pm 4.1%}$

Also, usefully, for any reported ${displaystyle MOE_{95}}$

${displaystyle MOE_{99}={frac {z_{0.99}}{z_{0.95}}}MOE_{95}approx 1.3times MOE_{95}}$

Specific margins of error[edit]

If a poll has multiple percentage results (for example, a poll measuring a single multiple-choice preference), the result closest to 50% will have the highest margin of error. Typically, it is this number that is reported as the margin of error for the entire poll. Imagine poll reports ${displaystyle p_{a},p_{b},p_{c}}$ as

${displaystyle MOE_{95}(P_{a})=z_{0.95}sigma _{overline {p_{a}}}approx 1.96{sqrt {frac {p_{a}(1-p_{a})}{n}}}=0.89/{sqrt {n}}=pm 2.8%}$

(as in the figure above)

${displaystyle MOE_{95}(P_{b})=z_{0.95}sigma _{overline {p_{b}}}approx 1.96{sqrt {frac {p_{b}(1-p_{b})}{n}}}=0.87/{sqrt {n}}=pm 2.7%}$

${displaystyle MOE_{95}(P_{c})=z_{0.95}sigma _{overline {p_{c}}}approx 1.96{sqrt {frac {p_{c}(1-p_{c})}{n}}}=0.27/{sqrt {n}}=pm 0.8%}$

As a given percentage approaches the extremes of 0% or 100%, its margin of error approaches ±0%.

Comparing percentages[edit]

Imagine multiple-choice poll reports ${displaystyle p_{a},p_{b},p_{c}}$ as . As described above, the margin of error reported for the poll would typically be ${displaystyle MOE_{95}(P_{a})}$ , as ${displaystyle p_{a}}$ is closest to 50%. The popular notion of statistical tie or statistical dead heat, however, concerns itself not with the accuracy of the individual results, but with that of the ranking of the results. Which is in first?

If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), and report result ${displaystyle p_{w}=p_{a}-p_{b}}$ , we could use the standard error of difference to understand how ${displaystyle p_{w_{1}},p_{w_{2}},p_{w_{3}},ldots }$ is expected to fall about ${displaystyle {overline {p_{w}}}}$ . For this, we need to apply the sum of variances to obtain a new variance, ${displaystyle sigma _{P_{w}}^{2}}$ ,

${displaystyle sigma _{P_{w}}^{2}=sigma _{P_{a}-P_{b}}^{2}=sigma _{P_{a}}^{2}+sigma _{P_{b}}^{2}-2sigma _{P_{a},P_{b}}=p_{a}(1-p_{a})+p_{b}(1-p_{b})+2p_{a}p_{b}}$

where ${displaystyle sigma _{P_{a},P_{b}}=-P_{a}P_{b}}$ is the covariance of ${displaystyle P_{a}}$ and ${displaystyle P_{b}}$ .

Thus (after simplifying),

${displaystyle {text{Standard error of difference}}=sigma _{overline {w}}approx {sqrt {frac {sigma _{P_{w}}^{2}}{n}}}={sqrt {frac {p_{a}+p_{b}-(p_{a}-p_{b})^{2}}{n}}}=0.029,P_{w}=P_{a}-P_{b}}$

${displaystyle MOE_{95}(P_{a})=z_{0.95}sigma _{overline {p_{a}}}approx pm {3.1%}}$

${displaystyle MOE_{95}(P_{w})=z_{0.95}sigma _{overline {w}}approx pm {5.8%}}$

Note that this assumes that $P_{{c}}$ is close to constant, that is, respondents choosing either A or B would almost never chose C (making ${displaystyle P_{a}}$ and ${displaystyle P_{b}}$ close to perfectly negatively correlated). With three or more choices in closer contention, choosing a correct formula for ${displaystyle sigma _{P_{w}}^{2}}$ becomes more complicated.

Effect of finite population size[edit]

The formulae above for the margin of error assume that there is an infinitely large population and thus do not depend on the size of population , but only on the sample size . According to sampling theory, this assumption is reasonable when the sampling fraction is small. The margin of error for a particular sampling method is essentially the same regardless of whether the population of interest is the size of a school, city, state, or country, as long as the sampling fraction is small.

In cases where the sampling fraction is larger (in practice, greater than 5%), analysts might adjust the margin of error using a finite population correction to account for the added precision gained by sampling a much larger percentage of the population. FPC can be calculated using the formula^[1]

${displaystyle operatorname {FPC} ={sqrt {frac {N-n}{N-1}}}}$

…and so, if poll were conducted over 24% of, say, an electorate of 300,000 voters,

${displaystyle MOE_{95}(0.5)=z_{0.95}sigma _{overline {p}}approx {frac {0.98}{sqrt {72,000}}}=pm 0.4%}$

${displaystyle MOE_{95_{FPC}}(0.5)=z_{0.95}sigma _{overline {p}}{sqrt {frac {N-n}{N-1}}}approx {frac {0.98}{sqrt {72,000}}}{sqrt {frac {300,000-72,000}{300,000-1}}}=pm 0.3%}$

Intuitively, for appropriately large ,

${displaystyle lim _{nto 0}{sqrt {frac {N-n}{N-1}}}approx 1}$

${displaystyle lim _{nto N}{sqrt {frac {N-n}{N-1}}}=0}$

In the former case, is so small as to require no correction. In the latter case, the poll effectively becomes a census and sampling error becomes moot.

References[edit]

^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. Blackwell Publishing. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)

Sources[edit]

Sudman, Seymour and Bradburn, Norman (1982). Asking Questions: A Practical Guide to Questionnaire Design. San Francisco: Jossey Bass. ISBN 0-87589-546-8
Wonnacott, T.H.; R.J. Wonnacott (1990). Introductory Statistics (5th ed.). Wiley. ISBN 0-471-61518-8.

External links[edit]

«Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. «Margin of Error». MathWorld.

Источник

Максимальная погрешность

Доверительные вероятности и интервал

Ошибки конечного ряда измерений

Введение

Формулы для нахождения относительной погрешности косвенных измерений

Расчёт ошибок косвенных измерений

Методики расчета

а a изм аист ед.изм. 4

Например: приборная погрешность

Что такое погрешность?

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

30 Поверка и калибровка си. Определения. Правовые основы.

Абсолютная погрешность — измерительный прибор

Как вычислить погрешность измерений?

В чем измеряется погрешность?

Как найти абсолютную погрешность измерительного прибора?

Что такое погрешность метода измерений?

Что такое погрешность измерительного прибора?

Как определить погрешность деления?

Как рассчитывается приведенная погрешность?

Как вычислить абсолютную погрешность формула?

Чему равна абсолютная погрешность?

Для чего нужна погрешность измерений?

Как найти абсолютную погрешность пример?

Как определить цену деления и погрешность?

Что такое максимальная погрешность измерений?

Как рассчитывается приведенная погрешность?

Как вычислить погрешность функции?

Как рассчитать абсолютную погрешность?

Concept[edit]

Standard deviation and standard error[edit]

Maximum margin of error at different confidence levels[edit]

Specific margins of error[edit]

Comparing percentages[edit]

Effect of finite population size[edit]

See also[edit]

References[edit]

Sources[edit]

External links[edit]

Не пропустите также:

Например:
приборная погрешность