Задача
1
1.
Определить максимальную абсолютную,
относительную, приведённую погрешности
и сделать запись результата измерения
напряжения аналоговым вольтметром с
классом точности 1,5 с пределом 1 В для
показания 0,87 В.
Решение
Для
аналогового вольтметра с классом
точности р = 1,5 максимальная абсолютная
погрешность равна (рис. 5.1):
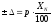
где
р – класс точности;
XN
– нормирующее значение измеряемой
величины, равное пределу измерения

В.
Приведённая
погрешность:
Относительная
погрешность:
В
соответствии с правилами округления
результат измерения имеет вид
0,870
В
Задача
2
Определить
абсолютную погрешность и сделать запись
результата измерения напряжения цифровым
вольтметром с классом точности 0,1/0,05 с
пределом 10 В для показания 7,93 В.
Решение
Для
цифрового вольтметра относительная
погрешность равна (рис.5.1):
Здесь
XK
= 10 В предел измерений;
c/d
= 0,1/0,05
– класс точности;
Х
=7,93 В – показание цифрового вольтметра.
По
относительной погрешности определяется
абсолютная:
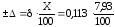
0,009 В
В
соответствии с правилами округления
результат измерения имеет вид
7,930
В
6.
Раздел
№6. «Обработка результатов прямых
многократных равноточных измерений»
6.1.
Основные положения
При
однократных измерениях оценку погрешности
производят на основе класса точности
используемых средств измерений (раздел
5).
Получаемый
при этом предел допускаемой погрешности
СИ неполно характеризует
качество измерений, т. е. остается
неизвестным закон распределения
вероятностей погрешностей и не ясно,
какая из составляющих систематическая
с
или случайная
доминируют в сумме
=
с
+
(6.1)
Для
того, чтобы оценить случайную погрешность
и определить более точно
усредненный результат измерения проводят
многократные наблюдения и статистическую
обработку их.
Структура
погрешности в каждой точке шкалы СИ
полностью характеризуется
плотностью распределения вероятностей.
Определение оценки плотности
распределения вероятностей (гистограммы)
требует проведения нескольких сотен
измерений
В
практике электроизмерений чаще всего
имеют дело с нормальным распределением.
Результаты
наблюдений, являющихся случайными
величинами X,
распределены по нормальному закону
(закону Гаусса), если их плотность
вероятностей
имеет вид
X
— математическое ожидание.
Для
решения многих задач не требуется знания
функции и плотности распределения
вероятностей, а вполне достаточными
характеристиками случайных
погрешностей служат их простейшие
числовые характеристики: математическое
ожидание и среднеквадратическое
отклонение. Числовые
вероятностные характеристики погрешностей,
представляющие собой неслучайные
величины, теоретически определяются
при конечном числе опытов.
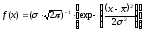
Где
— дисперсия;
Практически
число опытов всегда ограничено, поэтому
реально пользуются
числовыми характеристиками, которые
принимают за искомые вероятностные
характеристики и называют оценками
характеристик. Определение
оценок числовых характеристик может
быть выполнено по значительно
меньшему числу наблюдений N порядка
10-20).
Пусть
при измерении величины А, N
раз получен ряд значений X1,X2,Х3,
…
XN.
Если число измерений N достаточно велико,
то за истинное значение измеряемой
величины принимают наиболее достоверное
значение — среднее арифметическое
(действительное)
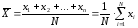
Зная
среднее арифметическое значение, можно
определить отклонение результата
единичного измерения от среднего
значения
i
=
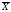
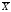
Это
отклонение может быть вычислено для
каждого измерения. Следует помнить, что
сумма отклонения результата измерений
от среднего значения равна нулю, а сумма
их квадратов минимальна. Эти свойства
используются при обработке результатов
измерений для контроля правильности
вычислений.
Среднее
квадратическое отклонение (СКО)
погрешности однократного измерения
σ равно

В
теории случайных погрешностей вводится
также понятие о среднем квадратическом
отклонении среднего арифметического
х
(средняя квадратическая погрешность
результата измерений)
(6.6)
где
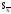
оценка средней квадратической погрешностих
ряда из N измерений.
При
оценке результатов измерений пользуются
понятием предельно допустимой
(максимальной) погрешности ряда измерений
макс
= 3
(6.7)
Рассмотренные
оценки результатов измерений, выражаемые
одним числом, называют точечными
оценками. Поскольку подобную оценку
обычно принимают за действительное
значение измеряемой величины, то
возникает вопрос
о точности и надежности полученной
оценки. Судят об этом по вероятности
того, что результат измерений
(действительное значение) отличается
от истинного не более чем на .
Это можно записать в виде
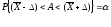
Вероятность
называется доверительной вероятностью
или

надежности, а интервал значений от
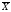
до
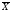
— доверительным интервалом. Обычно
его выражают в долях средней квадратической
погрешности
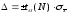
где
ta
(N)
— табулированный
коэффициент распределения Стьюдента,
который зависит
от доверительной вероятности
и
числа измерений N (таблица 6.1).
Результат
измерения записывается в виде
Х±;
(6.10)
При
расчетах необходимо пользоваться
правилами округления, изложенными
в разделе 5.
Коэффициенты
Стьюдента tα
для заданных значений
, N
Таблица
6.1
|
α N |
0,9 |
0,91 |
0,92 |
0,93 |
0,94 |
0,95 |
0,96 |
0,97 |
0,98 |
0,99 |
|
5 |
2,132 |
2,227 |
2,333 |
2,456 |
2,601 |
2,776 |
2,999 |
3,298 |
3,747 |
4,604 |
|
6 |
2,015 |
2,008 |
2,191 |
2,298 |
2,422 |
2,571 |
2,757 |
3,003 |
3,365 |
4,032 |
|
7 |
1,943 |
2,019 |
2,105 |
2,202 |
2,314 |
2,447 |
2,613 |
2,829 |
3,163 |
3,707 |
|
8 |
1,895 |
1,967 |
2,047 |
2,137 |
2,241 |
2,365 |
2,517 |
2,715 |
2,998 |
3,499 |
|
9 |
1,860 |
1,938 |
2,005 |
2,091 |
2,190 |
2,306 |
2,449 |
2,634 |
2,896 |
3,355 |
|
10 |
1,833 |
1,900 |
1,973 |
2,056 |
2,151 |
2,262 |
2,399 |
2,574 |
2,821 |
3,250 |
|
11 |
1,812 |
1,877 |
1,949 |
2,029 |
2,121 |
2,228 |
2,260 |
2,528 |
2,764 |
3,169 |
|
12 |
1,796 |
1,859 |
1,929 |
2,007 |
2,097 |
2,201 |
2,329 |
2,491 |
2,718 |
3,106 |
|
13 |
1,782 |
1,845 |
1,913 |
1,989 |
2,077 |
2,179 |
2,303 |
2,461 |
2,681 |
3,055 |
|
14 |
1,771 |
1,832 |
1,899 |
1,974 |
2,061 |
2,160 |
2,282 |
2,436 |
2,650 |
3,012 |
|
15 |
1,761 |
1,822 |
1,888 |
1,962 |
2,047 |
2,145 |
2,264 |
2,415 |
2,624 |
2,477 |
|
16 |
1,753 |
1,813 |
1,878 |
1,951 |
2,034 |
2,131 |
2,249 |
2,398 |
2,602 |
2,947 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Слайд 2
Задача 1. Определить максимальную абсолютную, относительную, приведѐнную
погрешности и сделать запись результата измерения напряжения
аналоговым вольтметром с классом точности 1,5 с пределом 1 В для показания 0,87 В.

Слайд 3
Решение: Для аналогового вольтметра с классом точности
р = 1,5 максимальная абсолютная погрешность равна
:
±∆ = p ∙XN/100 =1,5∙1/100 =0,015 B ,
где р – класс точности; XN – нормирующее значение измеряемой величины

Слайд 4
±γ =p% =1,5%
Приведѐнная погрешность: р% = 1,5%
±δ
= p∙XN/X = 1,5 ∙ 1/0.87 =1,72
Относительная погрешность: 1,72%
В соответствии с правилами округления результат измерения имеет вид 0,870 ± 0,015 В

Слайд 5
Задача 2. Определить абсолютную погрешность и сделать
запись результата измерения напряжения цифровым вольтметром с
классом точности 0,1/0,05 с пределом 10 В для показания 7,93 В.

Слайд 6
Решение Для цифрового вольтметра относительная погрешность равна
:
±δ=(с + d(XK/ X -1))=0,1 +
0,05 (10/7,93 -1 )=0,113%
Здесь XК = 10 В предел измерений; c/d = 0,1/0,05 – класс точности; Х =7,93 В – показание цифрового вольтметра.
По относительной погрешности определяется абсолютная:
±∆=δ ∙X/100 =0,113 ∙ 7,93/100=0,009 B
В соответствии с правилами округления результат измерения имеет вид 7,930± 0,009 В

Слайд 7
Задача 3.
Определить доверительный интервал и записать результат
измерения напряжения 37,86 В при погрешности однократного
измерения 0,14 В, если число измерений равно 5, доверительная вероятность 0,93.

Слайд 8
Решение: Доверительный интервал результата измерения при доверительной
вероятности равен ∆ = ± tα∙σ
tα — коэффициент распределения Стьюдента, зависящий от α и числа измерений N.
При α =0,93 и N= 5 в соответствии с табл.1 имеем значение t = 2,456.
Средняя квадратическая погрешность результата измерений х равна
σx= ± σ/N =0,14/√5 =0,0625 B

Слайд 9
Доверительный интервал результата измерения получается равным
∆
= ±2,456 ∙0,0623 = 0,153 В
Результат:
37,86 ±9,15B, α=0,93

Слайд 10
Задача 4. Дан результат измерения физической величины,
выраженный в делениях шкалы и равный α.
Дано: α = 49 дел., α макс = 150 дел., Iн = 7,5 А, Кл = 0,5.

Слайд 11
Измерение произведено прибором с указанными параметрами (класс
точности, верхний предел измерения, число делений шкалы).
Вычислить значение измеренной величины и наибольшую ожидаемую абсолютную и относительную погрешности. Записать результат измерения с учетом погрешности.

Слайд 12
Решение: 1) цена деления CI амперметра (вольтметра
– CB, ваттметра – СP)
равна
CI =Iн /αmax =7,5/150 =0,05 А/дел;
2) измеренное значение тока
I = α ∙ CI =49∙0,05 =2,45 A;
3) допускаемая наибольшая погрешность прибора
∆I =± K∙Iн /100 =±0,5∙7,5 /100 =±0,0375 A=0,04 A;

Слайд 13
4) наибольшая ожидаемая относительная погрешность измерения;
δI =
± ∆I∙100 / I = ± 0,04∙100
/2,45 = ±1,6 %
5) наибольшая ожидаемая абсолютная погрешность измерения равна наибольшей допускаемой погрешности прибора, т. е.
∆I =±0,04 A;
Результат измерения: I = 2,45 ±0,04 A= 2,45(1±0,016) A.

Слайд 14
Задача 5. Приведены данные ряда многократных замеров
частоты. Считая, что систематическая составляющая погрешности измерения
пренебрежимо мала, а случайные погрешности распределены по нормальному закону, вычислить среднее арифметическое значение результата частоты f ,оценку среднего квадратического значения случайной погрешности отдельного замера s,

Слайд 15
оценку среднего квадратического значения случайной погрешности в
определении среднего арифметического S. Проверить, нет ли
среди погрешностей отдельных измерений грубых погрешностей ( по правилу « 3-х сигм»). Задавшись доверительной вероятностью, вычислить границы доверительного интервала. Записать результат измерений.

Слайд 16
50,06; 49,82; 48,98: 50,30; 50,15; 50,08; 49,93;
49,76; 49,92; всего – 9 значений.
Решение:
1) определяем среднее арифметическое значение частоты:
x = ∑xi /n = (50,06 + 49,82+ 48,98 + 50,30+ 50,15+ 50,08+ 49,93+ 49,76+ 49,92) / 9 =50,003=50,00 Гц;
2) определяем оценку среднеквадратического отклонения отдельного замера S.
Для этого находим погрешности отдельных замеров: ∆i

Слайд 17
Получаем следующий ряд значений : +0,06;
–0,18; –0,02; +0,30; +0,15; +0,08; –0,07; 0,24;
–0,08.
Вычисляем S по формуле: S = √∑ ∆i2/ n-1 , S = ± 0,1674 Гц = ±0,17 Гц;

Слайд 18
3) проверим, имеются ли грубые ошибки (промахи)
по правилу: ∆i >3σ, 3S =0,51 Гц;
. Среди имеющихся девяти остаточных погрешностей наибольшая – в четвертом замере, равная 0,30 и не превосходит 3S = 0,51, поэтому повторного расчета S не требуется. В противном случае необходимо исключить грубые ошибки и вновь выполнить расчеты по пунктам 1 и 2;
4) находим оценку среднеквадратического отклонения (ошибки) среднего арифметического значения: Sx= ±S/√n =±0,1674/3 = ±0,0558 = ±0,06 Гц;

Слайд 19
5) определим границы доверительного интервала, приняв
доверительную вероятность равной Р = 0,95;
по
табл. 1. находим коэффициент Стьюдента tα для заданной доверительной вероятности
Р = 0,95 и n = 9: tα = 2,3;
доверительный интервал равен ∆ = ± tα ∙Sx =±2,3∙0,6 = ±0,138 =0,14 Гц;
6) результат измерения частоты x = 50,00 ±0,14 Гц, при Р = 0,95.

Слайд 20
Задача 6. Дано: α1 = 30 дел.,
α2 = 45 дел.
Амперметр: Кл=1,5, верхний
предел измерения тока Iн = 1,5 A,
αмакс = 75 дел.
Вольтметр: верхний предел измерения напряжения Uн = 300 В, αмакс = 150, Кл =1,0.

Слайд 21
Решение:
1) цена деления амперметра:
CI =Iн
/αmax =1,5/75 =0,02 А/дел;
2) наибольшая
допускаемая погрешность амперметра:
∆I =± K∙Iн /100 =±1,5∙1,5 /100 =±0,0225 A=0,02 A;
3) измеренный ток равен I = α ∙ CI =30∙0,02 =0,60 A;

Слайд 22
4) относительная погрешность измерения тока:
δI =
± ∆I / I = ± 0,0225
/0,6 = ±0,0375А=0,04А
5) цена деления вольтметра:
CU =Uн /αmax =300 / 150 = 2 B/дел;
6) наибольшая допускаемая погрешность вольтметра:
∆U =± K∙Uн /100 =±1,0∙ 300 /100 =± 3B;

Слайд 23
7) измеренное напряжение равно U= α2 ∙
CU =45∙ 2 =90 В;
 относительная
относительная
погрешность измерения напряжения составляет
δU = ± ∆U / U = ±3, / 90 = ±0,033B=0,03B
9) мощность и сопротивление резистора:
P = U ∙ I = 90 ∙ 0,6 =54 Bt, R = U / I = 90 / 0,6 = 150 Oм;

Слайд 24
10) относительная погрешность измерения мощности (наибольшая ожидаемая,
то же и для измерения сопротивления) равна
δP
= δR = δU + δI = ± ( 0,03 + 0,04) = ±0,07
т. к. и при умножении, и при делении двух измеренных значений относительная погрешность результата измерения равна сумме относительных погрешностей измерения каждого значения

Слайд 25
11) абсолютная погрешность и результат измерения мощности
составят
∆?= δ? ∙ ? = ±(0,07
∙ 54) = 3,78 ≈ 4 Вт, ? = (54 ± 4) Вт;
12) абсолютная погрешность и результат определении сопротивления:
∆?= δ? ∙ ? = ±(0,07 ∙ 150) = 10,5 ≈ 11 Ом, ? = (150 ± 11) Ом.

Систематические погрешности (ошибки) обычно остаются постоянными на протяжении всей серии измерений. Например, при переключении шкалы вольтметра с одного предела на другой меняется его внутреннее сопротивление, что может внести в последующие измерения систематическую погрешность.
Систематические погрешности надо стараться отслеживать и учитывать, корректируя полученные результаты, т.е. исправляя их на необходимую величину. Однако обнаружение систематических погрешностей требует, как правило, дополнительных более точных или альтернативных экспериментов, проведение которых невозможно в рамках лабораторных работ. В этих случаях достаточно указать возможный источник ошибок.
Все остальные погрешности являются случайными.
Промахи — грубые ошибки, обычно они связаны с неправильным отсчетом по шкале прибора, нарушением условий эксперимента и т.д. Их надо отбросить. В сомнительных случаях вопрос о том, является ли данный результат промахом, решают с помощью повторного, если возможно, более точного эксперимента или привлекая математические методы обработки полученных результатов, изучение которых лежит за рамками излагаемого элементарного анализа оценки погрешностей.
Приборные погрешности определяются двумя факторами:
1. классом точности прибора, связанным с его устройством – элементной базой и принципом действия.
Абсолютная погрешность через класс точности оценивается следующим образом:
(Dx) к.т.= (g/100)A,
где g — класс точности в %, указанный на панели прибора,
А= Аmax – предел измерения для стрелочных приборов, либо А есть текущее значение для магазинов сопротивления, индуктивности, емкости;
2. ценой делений шкалы прибора:
(Dx) ц.д.= h,
где h – цена деления шкалы прибора, т.е. расстояние между ближайшими штрихами шкалы, выраженное в соответствующих единицах измерения.
Погрешности разброса возникают вследствие различия экспериментальных значений при многократном повторении измерений одной и той же величины. Простейший способ определения (Dх)р дает метод Корнфельда, который предписывает следующий образ действий, если физическая величина х измерена n раз:
1) имея х1 , …,хn – значений измеряемой величины х, выбираем из хmax и хmin и находим среднее значение х:
;
2) находим абсолютную погрешность Dxр =
3) Записываем результат в виде: с
, где a — доверительная вероятность того, что истинное значение измеренной величины находится на отрезке
.
Доверительная вероятность определяет собой долю средних значений х, полученных в аналогичных сериях измерений, попадающих в доверительный интервал. (Эта формула доказывается в теории ошибок.)
Недостатком метода Корнфельда является то обстоятельство, что вероятность приводимого результата определяется исключительно количеством n проведенных измерений и не может быть изменена посредством увеличения или уменьшения доверительного интервала ± Dх. Такую возможность предусматривает несколько более сложный метод расчета погрешностей Стьюдента [2,3,7]. Последовательность расчета погрешностей этим методом такова:
1) Вы измерили и получили несколько i = 1,…,m значений случайной
величины i. Сначала исключаем промахи, то есть заведомо неверные
результаты.
2) По оставшимся n значениям определяем среднее значение величины :
.gif)
3) Определяем среднеквадратичную погрешность среднего значения :

i
4) Задаемся доверительной вероятностью a. По таблице коэффициентов
Стьюдента (Приложение 1) определяем по известному значению
числа измерений n и доверительной вероятности a коэффициент
Стьюдента tan.
5) Определяем погрешность среднего значения величины (доверительный интервал)
D= tan s<X>
6) Записываем результат
= (
± D
) с указанием доверительной вероятности a.
В научных статьях обычно приводят доверительный интервал
D = s<X>,
соответствующий доверительной вероятности α =0,7. Такой интервал называется стандартным, при его использовании часто значение доверительной погрешности не приводят. Использование метода Стьюдента является необходимым, когда требуется знать значение физических параметров с заданной доверительной вероятностью (как в ряде лабораторных работ). На практике доверительная вероятность погрешности разброса выбирается в соответствии с доверительной вероятностью, соответствующей классу точности измерительного прибора.
Для большинства исследований, в которых не выдвигается жестких требований к вероятности полученных результатов, метод Корнфельда является вполне приемлемым.
В теории ошибок показывается, что результирующая погрешность , если все эти погрешности рассчитаны для одной и той же доверительной вероятности. На практике, т.к. суммарная погрешность округляется до одной значащей цифры, достаточно выбрать максимальную из трех вычисленных погрешностей, и если она в 3 или более раз превосходит остальные, принять ее за погрешность измеренной величины, при этом фактор, с которым связана эта погрешность и будет в данном случае определять собой точность (а вернее — погрешность) эксперимента (подробнее см. в работе [1]).

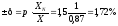
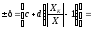
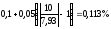
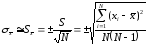
 относительная
относительная