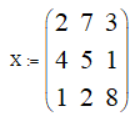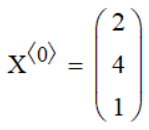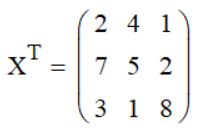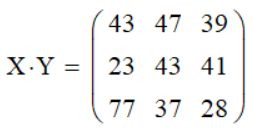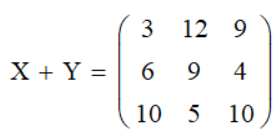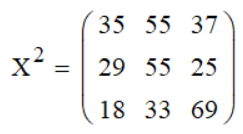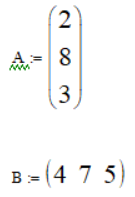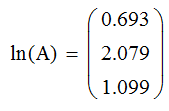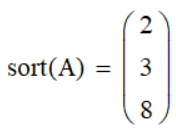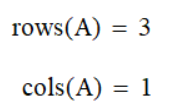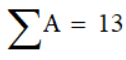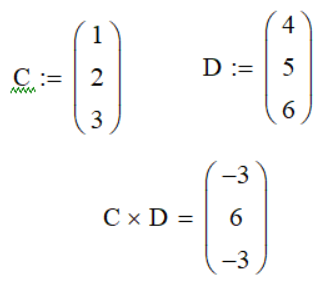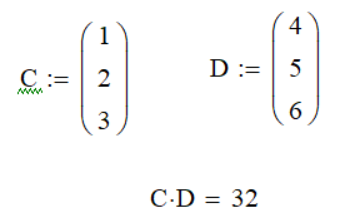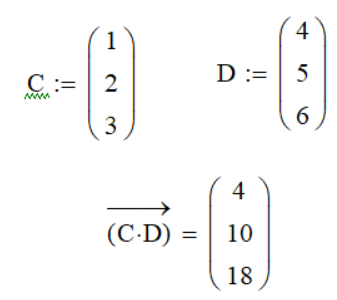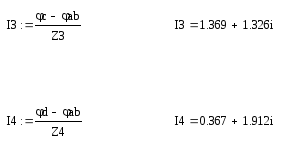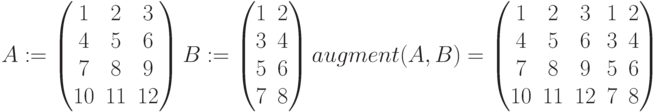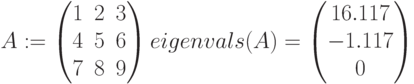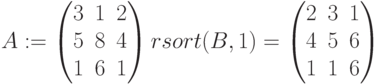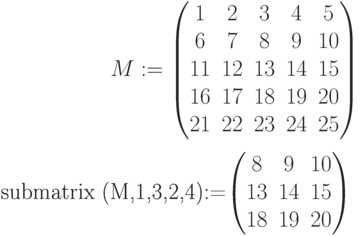Матрица в Mathcad
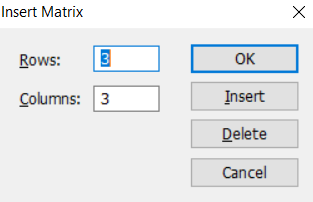
Для быстрого построения матрицы в Mathcad, нажмите Ctrl+M, появится окно Insert Matrix
Указываем размерность матрицы, rows – количество строк, columns – количество столбцов. Жмем Ок.
Вводим значения
Последний элемент матрицы равен (нумерация первого элемента начинается с нуля)
Найдем максимальное значение матрицы max(X)
Найдем минимальное значение матрицы min(X)
Среднее значение матрицы равно
Первая матрица-столбец равна
Транспонирование матрицы в Mathcad XT
Вычисление обратной матрицы
Вычисление определителя матрицы
Умножение матрицы на матрицу
Сложение матриц — сумма элементов матрицы Mathcad
Возведение матрицы в степень
Далее, создадим две матрицы в виде векторов 3×1 и 1×3
Здесь A – матрица-столбец; B – матрица-строка
Первый элемент вектора A (нумерация начинается с нуля) равен
Количество элементов в матрице-столбце через функцию length(A) равно
Найдем значения для функции ln x, подставив значения матрицы A
Сортировка вектора sort(А)
Количество элементов в векторе rows(A), cols(A)
Сумма вектора
Векторное произведение в Mathcad
Скалярное произведение
Векторизация
2896
Min(v)- возвращает
минимальный элемент
Re(v) -возвращает
вектор реальных частей вектора с
комплексными
переменными
Im(v)-то же для мнимых
частей
Приведенные
примеры помогут изучить методы расчёта
электрических цепей, сводящееся к
составлению уравнений Кирхгофа в
матричной форме и решение этих уравнений
в системе MathCAD.
Пример
2.1.
Рассмотрим цепь, изображенную на рис
1.2, параметры элементов цепи возьмём
как в примере 1.5. Требуется рассчитать
токи во всех ветвях различными методами.
Рассчитаем токи
во всех ветвях с помощью уравнений
Кирхгофа. Зададим данные:
где mE, aE — модуль
и аргумент (в радианах) значения ЭДС,
заданной в показательной форме;
mZ3, aZ3 — модуль и
аргумент сопротивления Z3.
В
все величины, заданные в показательной
форме, переведём в алгебраическую форму.
Далее составим
систему уравнений по законам Кирхгофа.
Предварительно запишем систему уравнений
в системе MathCAD не для вычисления, а как
комментарий:
Эти уравнения
записаны не по правилам записи в системе
MathCAD, и если бы мы оставили эти уравнения
для вычисления, то MathCAD непременно
показал ошибку. Эти уравнения нам
необходимы как комментарий. MathCAD
позволяет записывать математические
выражения как невычисляемые, для этого
необходимо:
— щелкнуть мышью
на данном формульном блоке, чтобы он
активизировался;
— щелкнуть на
кнопке меню Format;
— в этом меню
щелкнуть на кнопке Properties;
— в открывшемся
меню щелкнуть Calculation;
— в открывшемся
меню поставить «птичку» в Disable Evaluation;
— OK.
После этого в
правом верхнем углу активизированного
выражения появится чёрный квадратик,
указывающий на то, что выражение является
не вычисляемым, а используется как
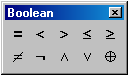
комментарий. Знак равенства в таких
выражениях следует брать как знак «=»
операции отношения из палитры
Boolean, открывается
при нажатии на соответствующую кнопку
на палитре Math.
Систему уравнений
(2.1) запишем в матричной форме.
г
Зададим в системе
MathCAD матрицы А и В.
Сначала запишем
А:= .
Затем зададим
шаблон матрицы размером 6х6 и получим
Д
наводим курсор на соответствующий
элемент шаблона матрицы, щелкаем мышью
и с клавиатуры вводим значения элемента
в виде математического выражения. Все
переменные этого выражения должны быть
предварительно определены, иначе MathCAD
покажет на ошибку.
А
создадим вектор — столбец правой части.
Для нахождения вектора искомых токов записываем
гдеоперация вычисления матрицы, обратной
А.
Результат вычисления
токов вы ведем на экран:
Теперь выполним
тот же самый расчёт методом контурных
токов.
П
обход всех независимых контуров по
часовой стрелке и обозначим контурные
токи I11, I22, I33. Тогда система контурных
уравнений примет вид:
В матричной форме эта система запишется
где
— матрица сопротивлений системы контурных
уравнений;
— вектор — столбец
контурных токов;
— вектор столбец
контурных ЭДС.
Запишем
и
в системе MathCAD.
Т
исходные контурные токи можно получить:
П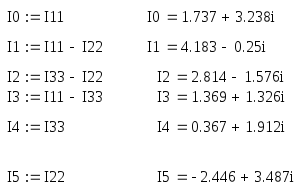
токи ветвей.
Н
выполним тот же расчёт методом узловых
потенциалов. Непосредственно для
исходной цепи, изображенной на рис 1.2,
метод узловых потенциалов применять
нельзя, т.к. проводимость ветви содержащей
источник ЭДС, равно бесконечности.
Поэтому сделаем эквивалентное
преобразование цепи путём переноса
источника в смежные ветви ad и ac. После
этого узлы а и b объединятся в один узел
аb. После такого преобразования цепь
примет вид, показанный на рис.2.1.
Рисунок 2.1 — Схема
электрической цепи на рис 1.2 после
переноса ЭДС.
Преобразованная
цепь имеет три узла ab, c, d. Положим
потенциал одного из узлов, например ab,
равным нулю:,
тогда для узлов с, d система потенциальных
уравнений имеет вид:
Или в матричной
форме:
В системе MathCAD
запишем выражения для вычисления
элементов матрицы Y и I.
Напомним, что в
матрице Y
только диагональные элементы имеют
знак плюс, а остальные – знак минус.
Диагональные элементы имеют следующий
смысл: Ycc
есть сумма проводимостей ветвей,
сходящихся к узлу «с», Ydd
– сумма проводимостей ветвей, сходящихся
к узлу «d».
Определим токи в
ветвях.
Вывод: Все методы
расчёта дали один и тот же результат,
следовательно, расчёты верны. Наиболее
простым для данной цепи является метод
контурных токов.
Соседние файлы в папке 2. Самоучители Derive+MathCAD
- #
- #
- #
- #
20.04.20153.66 Кб8Содержание OneNote.onetoc2
Slawa писал(а):А что делает функция match? (не нахожу я ее в help).
Наравне с мин/макс значением меня интересует НОМЕР его элемента (координаты) в матрице. Есть что- то подобное в маткаде?
Кроме функции match есть функции для построчного/»постолбцового» поиска:
lookup(z, A, B) Looks in a vector or matrix, A, for a given value, z, and returns the value(s) in the same position(s) (i.e., with the same row and column numbers) in another matrix, B. When multiple values are returned, they appear in a vector in row-wise order, starting with the top left corner of B and sweeping to the right.
hlookup(z, A, r) Looks in the first row of a matrix, A, for a given value, z, and returns the value(s) in the same column(s) in the row specified, r. When multiple values are returned, they appear in a vector.
vlookup(z, A, c) Looks in the first column of a matrix, A, for a given value, z, and returns the value(s) in the same row(s) in the column specified, c. When multiple values are returned, they appear in a vector.
В М11 есть, по идее должны быть и М2000/2001
MathCAD: cделай это по-разному…
Просто пара-тройка «весёлых картинок» с занятий по MathCAD, чтоб не выкидывать, версия — Prime II или III, или 15-я, какая попалась:
4 способа извлечь строку из матрицы
2 способа найти скалярное произведение векторов
2 способа узнать длину вектора
Перестановка местами максимального и минимального элемента матрицы. На самом деле, условие не совсем корректно. Если максимальный и минимальный элементы единственны или нужны только первые их вхождения (или последние, если поменять знаки «<«, «>» на «≤», «≥»), то достаточно следующего «школьного» и однопроходного кода:
Перестановка местами максимального и минимального элемента матрицы (только одна)
Если же нужно все вхождения минимального элемента заменить на максимальный и наоборот, придётся делать 2 прохода по матрице, примерно так:
Перестановка местами максимального и минимального элемента матрицы (все вхождения)
Конечно, значения максимума и минимума можно было найти стандартными функциями max, min, но они всё равно бы делали такой же проход.
Тем не менее, обмен местами минимальных и максимальных значений легко было бы сделать и без программирования (приведён пример для вектора):
обмен местами минимальных и максимальных значений в векторе без написания подпрограммы-функции
То же самое — с определением номера максимального элемента вектора. Корректно было бы вернуть вектор, состоящий из всех номеров максимальных элементов, на случай, если их несколько:
список номеров элементов вектора, которые совпадают с максимальным
В матрице найти номера строк, суммы элементов которых максимальны, учесть, что строк может быть больше одной:
Mathcad, номера строк, суммы элементов которых максимальны
Решаем символьно квадратное уравнение и сразу же упрощаем вид полученных mathcad формул:
Решаем символьно квадратное уравнение
09.06.2015, 16:19 [12851 просмотр]
Часто используемые функции
augment(A,B) — Возвращает матрицу, сформированную путем размещения массива В справа от массива А. А и В должны иметь одинаковое число строк:
ceil(y) – возвращает наименьшее целое, большее или равное y. Значение y должно быть вещественным числом:
cols(A) – число столбцов матрицы А.
csort(B,n) – сортирует строки матрицы В таким образом, чтобы расположить элементы столбца n в порядке возрастания. Нумерация столбцов по умолчанию начинается с нуля:
eigenvals(A) – определяет вектор собственных значений для квадратной матрицы А:
find(x,y,…) – возвращает значения x,y,…, удовлетворяющие ограничениям: равенствам или неравенствам, заданным в блоке given решения уравнений. Число уравнений должно равняться числу неизвестных.
floor(y) – возвращает наибольшее целое, меньшее или равное y. Значение y должно быть вещественным числом:
identity(n) – создает единичную матрицу размером
, в которой диагональные элементы равны 1, а остальные элементы равны 0:
length(v) – длина вектора v.
max(v) – максимальный по значению элемент вектора v.
min(v) – минимальный по значению элемент вектора v.
maximize(f,v) – возвращает вектор размерности n, который обеспечивает функции f максимальное значение. Функция f – функция n переменных; вектор v – вектор начальных приближений ответа;
minimize(f,v) — возвращает вектор размерности n, который обеспечивает функции f минимальное значение. Обращение аналогично функции Maximize.
mean(M) – среднее арифметическое элементов вектора или матрицы.
median(v) – медиана вектора. Элементы вектора должны быть заданы в порядке возрастания:
rbeta (m, s 1, s2)Возвращает вектор m случайных чисел, имеющих бэта-распределение. 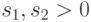
rbinom (m, n, p) Возвращает вектор m случайных чисел, имеющих биномиальное распределение. 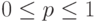
rgamma (m, s) Возвращает вектор m случайных чисел, имеющих гамма- распределение, 
rgeom (m, p) Возвращает вектор m случайных чисел, имеющих геометрическое распределение. 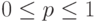
rlogis (m, l, s) Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а 
rnorm (m,l, s) Возвращает вектор m случайных чисел, имеющих нормальное распределение. 
rpois (m,d) Возвращает вектор m случайных чисел, имеющих распределение Пуассона. 
rt (m, d) Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента.
runif (m, a, b) Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. 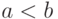
rnd (x) Возвращает равномерно распределенное случайное число между 0 и x. Эквивалент runif (1, 0, x).
round(y,n) – округляет вещественное число y до n знаков справа от десятичной точки. Если n отсутствует, то y округляется до ближайшего целого числа. Если n<0, то y округляется до n знаков слева от десятичной точки.
rows(A) – число строк матрицы А.
rsort(B,n) – сортирует столбцы матрицы В таким образом, чтобы расположить элементы строки n в порядке возрастания:
Нумерация строк по умолчанию начинается с нуля.
submatrix(M,ir,jr,ic,jc) – подматрица, состоящая из элементов матрицы М, содержащихся в строках от ir до jr и столбцах от ic до jc: