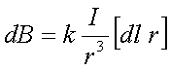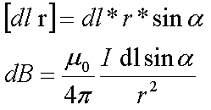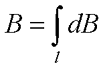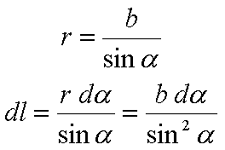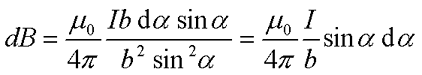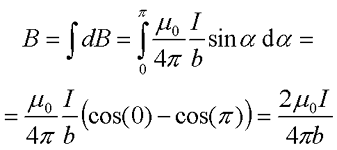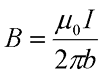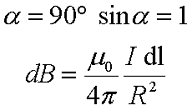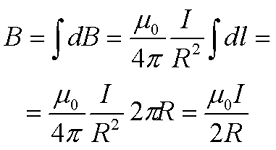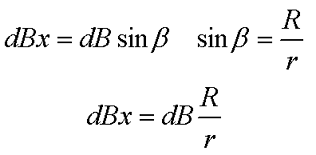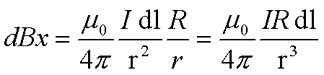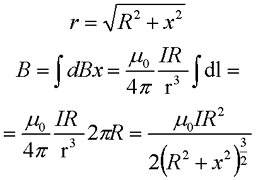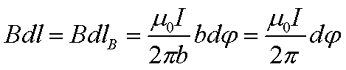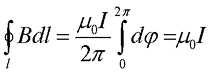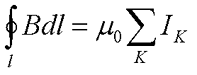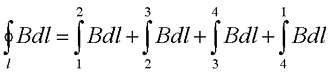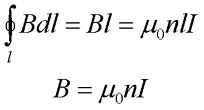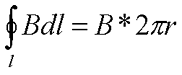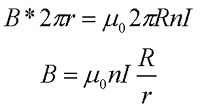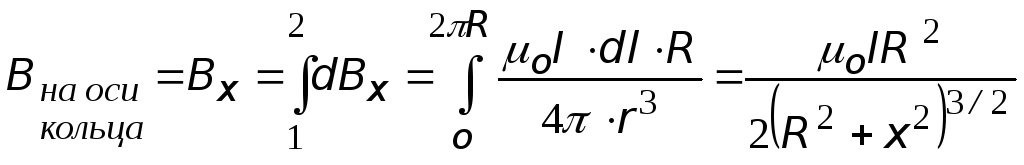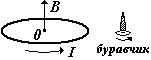Как найти магнитную индукцию в центре кольца

Всем доброго времени суток. В прошлой статье я рассказал о магнитном поле и немного остановился на его параметрах. Данная статья продолжает тему магнитного поля и посвящена такому параметру как магнитная индукция. Для упрощения темы я буду рассказывать о магнитном поле в вакууме, так как различные вещества имеют разные магнитные свойства, и как следствие необходимо учитывать их свойства.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Закон Био – Савара – Лапласа

В результате исследования магнитных полей создаваемых электрическим током, исследователи пришли к таким выводам:

• магнитная индукция, создаваемая электрическим током пропорциональна силе тока;
• магнитная индукция имеет зависимость от формы и размеров проводника, по которому протекает электрический ток;
• магнитная индукция в любой точке магнитного поля зависит от расположения данной точки по отношению к проводнику с током.

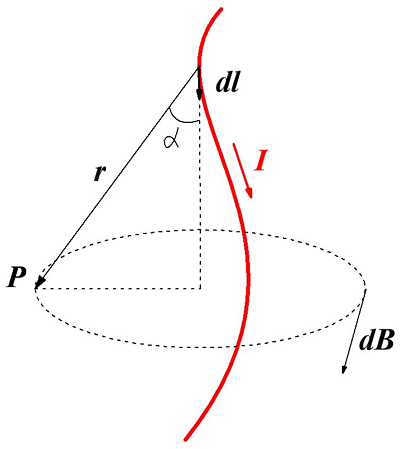
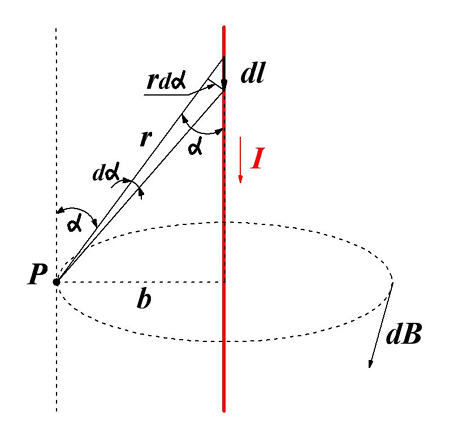
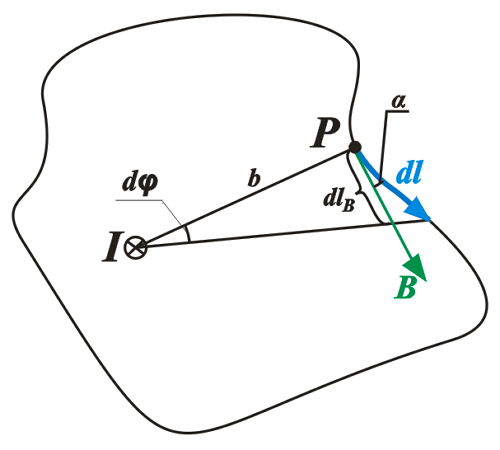
Французские учёные Био и Савар, которые пришли к таким выводам обратились к великому математику П. Лапласу для обобщения и вывода основного закона магнитной индукции. Он высказал гипотезу, что индукция в любой точке магнитного поля, создаваемое проводником с током можно представить в виде суммы магнитных индукций элементарных магнитных полей, которые создаются элементарным участком проводника с током. Данная гипотеза и стала законом магнитной индукции, называемого законом Био – Савара – Лапласа. Для рассмотрения данного закона изобразим проводник с током и создаваемую им магнитную индукцию

Магнитная индукция dB, создаваемая элементарным участком проводника dl.

Тогда магнитная индукция dB элементарного магнитного поля, которое создается участком проводника dl, с током I в произвольной точке Р будет определяться следующим выражением

где I – сила тока, протекающая по проводнику,

r – радиус-вектор, проведённый от элемента проводника к точке магнитного поля,

dl – минимальный элемент проводника, который создает индукцию dB,

k – коэффициент пропорциональности, зависящий от системы отсчёта, в СИ k = μ₀/(4π)

Так как [dl r] является векторным произведением, тогда итоговое выражение для элементарной магнитной индукции будет выглядеть следующим образом

Таким образом, данное выражение позволяет найти магнитную индукцию магнитного поля, которое создается проводником с током произвольной формы и размеров при помощи интегрирования правой части выражения

где символ l обозначает, что интегрирование происходит по всей длине проводника.

Магнитная индукция прямолинейного проводника

Как известно простейшее магнитное поле создает прямолинейный проводник, по которому протекает электрический ток. Как я уже говорил в предыдущей статье, силовые линии данного магнитного поля представляют собой концентрические окружности расположенные вокруг проводника.

Магнитная индукция магнитного поля создаваемого прямолинейным проводником с током.

Для определения магнитной индукции В прямого провода в точке Р введем некоторые обозначения. Так как точка Р находится на расстоянии b от провода, то расстояние от любой точки провода до точки Р определяется как r = b/sinα. Тогда наименьшую длину проводника dl можно вычислить из следующего выражения

В итоге закон Био – Савара – Лапласа для прямолинейного провода бесконечной длины будет иметь вид

где I – ток, протекающий по проводу,

b – расстояние от центра провода до точки, в которой рассчитывается магнитная индукция.

Теперь просто проинтегрируем получившееся выражение по dα в пределах от 0 до π.

Таким образом, итоговое выражение для магнитной индукции прямолинейного провода бесконечной длины будет иметь вид

где μ₀  – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

I – ток, протекающий по проводу,

b – расстояние от центра проводника до точки, в которой измеряется индукция.

Магнитная индукция кольца

Индукция прямого провода имеет небольшое значение и уменьшается при удалении от проводника, поэтому в практических устройствах практически не применяется. Наиболее широко используются магнитные поля созданные проводом, намотанным на какой либо каркас. Поэтому такие поля называются магнитными полями кругового тока. Простейшим таким магнитным поле обладает электрический ток, протекающий по проводнику, который имеет форму окружности радиуса R.

В данном случае практический интерес представляет два случая: магнитное поле в центре окружности и магнитное поле в точке Р, которое лежит на оси окружности. Рассмотрим первый случай.

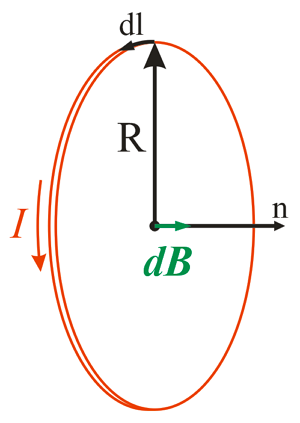
Магнитная индукция в центре кругового тока.

В данном случае каждый элемент тока dl создаёт в центре окружности элементарную магнитную индукцию dB, которая перпендикулярна к плоскости контура, тогда закон Био-Савара-Лапласа будет иметь вид

Остается только проинтегрировать полученное выражение по всей длине окружности

где μ₀  – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

I – сила тока в проводнике,

R – радиус окружности, в которое свернут проводник.

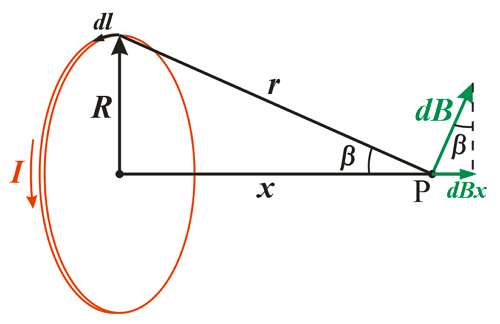
Рассмотрим второй случай, когда точка, в которой вычисляется магнитная индукция, лежит на прямой х, которая перпендикулярна плоскости ограниченной круговым током.

Магнитная индукция в точке, лежащей на оси окружности.

В данном случае индукция в точке Р будет представлять собой сумму элементарных индукций dB_X, которые в свою очередь представляет собой проекцию на ось х элементарной индукции dB

Применив закон Био-Савара-Лапласа вычислим величину магнитной индукции

Теперь проинтегрируем данное выражение по всей длине окружности

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

I – сила тока в проводнике,

R – радиус окружности, в которое свернут проводник,

х – расстояние от точки, в которой вычисляется магнитная индукция, до центра окружности.

Как видно из формулы при х = 0, получившееся выражение переходит в формулу для магнитной индукции в центре кругового тока.

Циркуляция вектора магнитной индукции

Для расчёта магнитной индукции простых магнитных полей достаточно закона Био-Савара-Лапласа. Однако при более сложных магнитных полях, например, магнитное поле соленоида или тороида, количество расчётов и громоздкость формул значительно увеличится. Для упрощения расчётов вводится понятие циркуляции вектора магнитной индукции.

Циркуляция вектора магнитной индукции по произвольному контуру.

Представим некоторый контур l, который перпендикулярный току I. В любой точке Р данного контура, магнитная индукция В направлена по касательной к данному контуру. Тогда произведение векторов dl и В описывается следующим выражением

Так как угол dφ достаточно мал, то векторов dl_В определяется, как длина дуги

Таким образом, зная магнитную индукцию прямолинейного проводника в данной точке, можно вывести выражение для циркуляции вектора магнитной индукции

Теперь остаётся проинтегрировать получившееся выражение по всей длине контура

В нашем случае вектор магнитной индукции циркулирует вокруг одного тока, в случае же нескольких токов выражение циркуляции магнитной индукции переходит в закон полного тока, который гласит:

Циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, которые охватывает данный контур.

Магнитное поле соленоида и тороида

С помощью закона полного тока и циркуляции вектора магнитной индукции достаточно легко определить магнитную индукцию таких сложных магнитных полей как у соленоида и тороида.

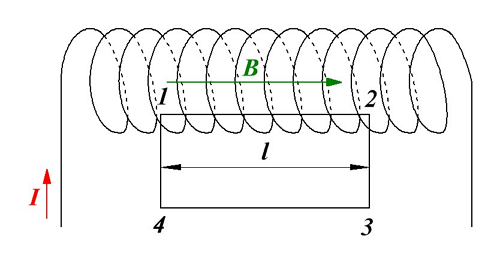
Соленоидом называется цилиндрическая катушка, которая состоит из множества витков проводника, намотанных виток к витку на цилиндрический каркас. Магнитное поле соленоида фактически состоит из множества магнитных полей кругового тока с общей осью, перпендикулярной к плоскости каждого кругового тока.

Магнитная индукция соленоида.

Воспользуемся циркуляцией вектора магнитной индукции и представим циркуляцию по прямоугольному контуру 1-2-3-4. Тогда циркуляция вектора магнитной индукции для данного контура будет иметь вид

Так как на участках 2-3 и 4-1 вектор магнитной индукции перпендикулярен к контуру, то циркуляция равна нулю. На участке 3-4, который значительно удалён от соленоида, то его так же можно не учитывать. Тогда с учётом закона полного тока магнитная индукция в соленоиде достаточно большой длины будет иметь вид

где n – число витков проводника соленоида, которое приходится на единицу длины,

I – ток, протекающий по соленоиду.

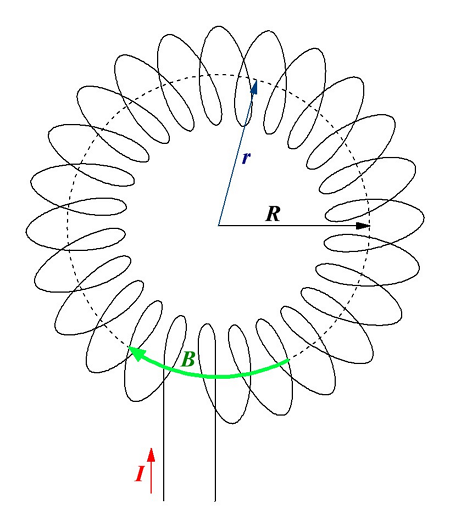
Тороид образуется путём намотки проводника на кольцевой каркас. Данная конструкция эквивалентна системе из множества одинаковых круговых токов, центры которых расположены на окружности.

Магнитная индукция тороида.

В качестве примера рассмотрим тороид радиуса R, на который намотано N витков провода. Вокруг каждого витка провода возьмём контур радиуса r, центр данного контура совпадает в центром тороида. Так как вектор магнитной индукции B направлен по касательной к контуру в каждой точке контура, то циркуляция вектора магнитной индукции будет иметь вид

где r – радиус контура магнитной индукции.

Контур проходя внутри тороида охватывает N витков провода с током I, тогда закон полного тока для тороида будет иметь вид

где n – число витков проводника, которое приходится на единицу длины,

r – радиус контура магнитной индукции,

R – радиус тороида.

Таким образом, используя закон полного тока и циркуляцию вектора магнитной индукции можно рассчитать сколь угодно сложное магнитное поле. Однако закон полного тока дает правильные результаты только лишь в вакууме. В случае расчёта магнитной индукции в веществе необходимо учитывать так называемые молекулярные токи. Об этом пойдёт речь в следующей статье.

Французские ученые Ж. Био и Ф. Савар изучали магнитные поля, создаваемые постоянными токами разной формы. Результаты их работы обобщил известный математик и физик П. Лаплас.

Применение закона Био – Савара – Лапласа к вычислению магнитного поля кругового тока

Закон Био-Савара–Лапласа описывает порождение магнитного поля током $I$ на элементе проводника длиной $dl$ в некоторой точке пространства ($mu$ — магнитная проницаемость вещества в котором локализовано поле):

$dvec{B}=frac{mu_{0}mu }{4pi }frac{Ileft[ dvec{l}vec{r}right]}{r^{3}}left( 1 right)$

где $d vec l ⃗$ — вектор, длина которого равна длине элемента проводника $dl$, направленный по току; $vec r$ – радиус-вектор, который проведен от элемента $dl$ в точку, в которой исследуется магнитное поле. Поскольку в правой части формулы (1) находится векторное произведение, очевидно, что индукция элементарного магнитного поля будет направлена перпендикулярно плоскости, в которой находятся векторы $vec r$ и $vec l$ и при этом является касательной к силовой линии поля.

Величину вектора $vec{dB}$ из выражения (1) найдем как:

$dB=frac{mu_{0}mu }{4pi }frac{Idlsin alpha }{r^{2}}left( 2 right)$.

где $ alpha $– угол между векторами $vec r$ и $vec l$ .

Конкретное направление $vec{dB}$ находят по правилу буравчика (правилу правой руки):

Если правый винт вращать так, что его поступательное движение будет совпадать с направлением течения тока в избранном элементе, то вращение его головки укажет направление $vec{dB}$.

Магнитные поля подчиняются принципу суперпозиции:

Суммарную магнитную индукцию поля, создаваемого несколькими источниками, находят как геометрическую сумму векторов магнитной индукции отдельных полей:

$vec{B}=sumlimits_{i=1}^N vec{B}_{i} left( 3 right). $

Если распределение токов можно считать непрерывным, то принцип суперпозиции можно записать:

$vec{B}=int {dvec{B}_{i}} left( 4 right).$

Вычисление магнитной индукции поля с применением закона Био-Савара-Лапласа довольно сложная процедура. Но при существовании определенной симметрии в распределении токов, используя, рассмотренный нами закон и принцип суперпозиции, рассчитать конкретные поля просто. В любом случае следует придерживаться следующей схемы действий:

1. Выделить на проводнике с током элементарный отрезок $dl$.
2. Записать для исследуемой точки поля закон Био – Савара – Лапласа.
3. Определить направление элементарного поля $vec{dB}$ в избранной точке.
4. Воспользоваться принципом суперпозиции для магнитных полей (учесть, что суммируются векторы).

Магнитное поле кругового тока в его центре

Рассмотрим круговой проводник, по которому течет постоянный ток $I$ (рис.1). Выделим на этом проводнике элемент $dl$, который можно считать прямолинейным. Если перейти к другому элементу этого же тока, затем к третьему и так далее, применить правило правого винта, то очевидно, что все магнитные поля, созданные этими элементами в центре, направлены вдоль одной прямой, перпендикуляру к плоскости кольца. Это означает, применяя принцип суперпозиции, мы векторное сложение заменим алгебраическим.

Запишем закон Био-Савара-Лапласа для модуля вектора индукции поля, создаваемого элементом d$l_1$:

$dB=frac{mu_{0}mu }{4pi }frac{Idl_{1}sin alpha }{r^{2}}left( 5right).$

Из рис.1 мы видим:

1. что расстояние от элементарного тока до центра витка равно его радиусу ($R$) и будет одинаковым для всех элементов на этом витке,
2. элемент $dl$ (как и все остальные элементы) будут нормальны к радиус-вектору $vec r$.

Учитывая сказанное выражение (5) представим в виде:

$dB=frac{mu_{0}mu }{4pi }frac{Idl_{1}}{R^{2}}left( 6 right)$.

Обезличивая витки с током, положим далее $dl_1=dl$.

Поскольку наш ток является непрерывным, то для нахождения полного поля в его центре, мы проинтегрируем (6), имеем:

$B=ointlimits_L {dB=} frac{mu_{0}mu }{4pi}frac{I}{R^{2}}ointlimits_L {dl} =frac{mu_{0}mu }{4pi}frac{I}{R^{2}}2pi Rto$

$B=mu_{0}mu frac{I}{2R}left( 7 right)$.

Индукция магнитного поля кругового тока на его оси

Найдем индукцию магнитного поля на оси кругового тока, если ток, текущий по нему равен $I$, радиус витка — $R$ (рис.2).

Как основу для выполнения поставленной задачи возьмем закон Био-Савара-Лапласа (1), где из рис.2 мы видим, что:

• $vec{r}=vec{R}+vec{h}$,

• $dvec{l}times vec{r}=dvec{l}times vec{R}+dvec{l}times vec{h}(9).$

Используя принцип суперпозиции закон (1) для нашего тока и формулы (8-9) запишем:

$vec{B}=ointlimits_L {dB=}$$frac{mu mu_{0}}{4pi }Iointlimits_L frac{dvec{l}timesvec{r}}{r^{3}} $
$=frac{mu mu_{0}}{4pi }frac{I}{r^{3}}left( ointlimits_L{dvec{l}times vec{R}+} ointlimits_L {dvec{l}times vec{h}}right)left( 10 right).$

В выражении (10) при записи интеграла, мы учли, что величина вектора $vec{r}$ не изменяется. Кроме этого вектор $vec h$, определяющий положение точки, в которой мы ищем поле, не изменяется при движении по нашему контуру, поэтому:

$ointlimits_L {dvec{l}times vec{h}} =(ointlimits_L {dvec{l})timesvec{h}} =0, left( 11 right),$

так как ( $ointlimits_L {dvec{l})=0.}$

Вычислим интеграл: $ointlimits_L {dvec{l}times vec{R}.}$ Введем единичный вектор ($vec n$), нормальный к плоскости витка с током.

$ointlimits_L {dvec{l}times vec{R}=ointlimits_L {vec{n}Rdl=vec{n}R}} ointlimits_L {dl=vec{n}R} 2pi R=2pi R^{2}vec{n}left( 12 right)$.

Подставляем результаты интегрирования из (12) в (10), имеем:

$vec{B}=frac{mu mu_{0}}{4pi }frac{I}{r^{3}}2pi R^{2}vec{n}=frac{mumu_{0}I}{2}frac{R^{2}}{left( R^{2}+h^{2}right)^{frac{3}{2}}}vec{n}left( 13 right)$

где при записи окончательного результата мы учли, что:

$r^{3}=left( R^{2}+h^{2} right)^{frac{3}{2}}$.

Кольца Гельмгольца

Кольцами Гельмгольца считают пару проводников в виде колец одного радиуса, расположенных в параллельных плоскостях (рис.3) на одной оси. Расстояние между плоскостями колец равно их радиусу.

Рассмотрим магнитное поле на оси этих колец.

Декартову систему координат разместим так, что ее начало совпадает с центром нижнего кольца с током. Ось Z нашей системы будет направлена по оси колец (рис.3).

Запишем индукцию магнитного поля в точке с координатой $z$ на оси колец. Используем формулу (13):

$B_{z}=frac{mu mu_{0}I}{2}R^{2}left[ frac{1}{left( R^{2}+z^{2}right)^{frac{3}{2}}}+frac{1}{left[ left( z-d right)^{2}+R^{2}right]^{frac{3}{2}}} right]left( 14right)$.

Исследуем полученное поле. Считается, что магнитное поле на оси колец Гельмгольца на посередине между ними является однородным.

Неоднородность в первом приближении характеризуют первой производной:

$frac{partial B_{z}}{partial z}=frac{3mu mu_{0}I}{2}R^{2}left[frac{-z}{left( R^{2}+z^{2} right)^{frac{5}{2}}}+frac{z-d}{left[ left(z-d right)^{2}+R^{2} right]^{frac{5}{2}}} right]left( 15 right)$.

Если $z=frac{d}{2}quad$ , подставим в (15), имеем:

$frac{partial B_{z}}{partial z}=0.$

Найдем $frac{partial^{2}B_{z}}{partial z^{2}}:$

$frac{partial^{2}B_{z}}{partial z^{2}}=frac{3mu mu_{0}I}{2}R^{2}left( frac{5z^{2}}{left( R^{2}+z^{2}right)^{frac{7}{2}}}-frac{1}{left( R^{2}+z^{2}right)^{frac{5}{2}}}+frac{5left( z-d right)^{2}}{left[ left( z-d right)^{2}+R^{2} right]^{frac{7}{2}}}-frac{1}{left[ left( z-dright)^{2}+R^{2} right]^{frac{5}{2}}} right)left( 16 right)$

По условию для колец Гельмгольца, имеем:
$d=R.$

На середине их общей оси ($z=frac{d}{2})$, получаем:

$frac{partial^{2}B_{z}}{partial z^{2}}=0, left( 17 right)$.

Равенство нулю второй производной от $B_z$ по координате $z$, показывает, что в на середине оси колец магнитное поле является однородным с высокой степенью точности.

46

ВОЛОДИНА Л. А., доцент кафедры физики
РГУ им.Губкина «Электромагнетизм и
волны» (конспект, прод.6)

МАГНИТНОЕ
ПОЛЕ В ВАКУУМЕ

Сила Лоренца.

Неподвижные в
некоторой системе отсчета К
электрические
заряды взаимодействуют между собой с
кулоновской (электростатической) силой.
Если эти заряды рассматривать, находясь
в другой системе отсчета К,
движущейся
относительно системы К
с постоянной
скоростью
v,
и использовать формулы релятивистской
механики, то выражение для силы
взаимодействия зарядов оказывается
другим.¹
Появляется дополнительная сила,
зависящая от скорости. Эту дополнительную
силу называют магнитной силой. Кулоновская
сила зависит от расстояния между
зарядами, магнитная сила зависит от
скорости движения зарядов. Полную силу
взаимодействия зарядов называют силой
Лоренца или электромагнитной силой.

Это выражение для
силы Лоренца следует из теории
относительности – из инвариантности
релятивистского уравнения движения
².
Можно сказать, что это выражение является
релятивистским обобщением закона
Кулона. Второе слагаемое F_магн
можно назвать
также релятивистской добавкой к
кулоновской силе. Из теории относительности
следует, что отношение
F_магн
/F_эл
= v²/c²
,

где v
– скорость движения заряда, с
– скорость света в вакууме, т.е. магнитная
часть силы Лоренца F_магн

F_эл
.Для отдельного заряда эти силы становятся
сравнимы при очень больших скоростях.
Однако, и при малых скоростях магнитная
сила оказывается заметной. Например,
когда по проводнику течет ток, электрическое
поле движущихся отрицательных зарядов
нейтрализуется полем положительных
зарядов. В результате остается одна
магнитная сила, именно она проявляется
при взаимодействии проводников с током
(сила Ампера).

Магнитное поле.
Вектор магнитной индукции.

Вокруг неподвижного
электрического заряда существует
электростатическое поле, которое
характеризуют вектором напряженности
Е,
посредством этого поля осуществляется
взаимодействие данного заряда с другими
неподвижными зарядами, находящимися в
этом поле. Если электрический заряд
движется,
вокруг него, а также вокруг проводника
с током (ток – это движущиеся направленно
заряды) возникает поле, которое называют
магнитным
полем и
характеризуют вектором В

вектором
магнитной индукции. Это поле действует
на другие движущиеся
заряды и
проводники с током
с силой,
которую называют магнитной
силой.

Физический смысл
вектора В
можно определить из выражений для
магнитных
сил.

Из формулы ():
B=
F_max/(qv)

магнитная индукция численно равна
максимальной силе, действующей на
единичный положительный заряд, движущийся
в магнитном поле с единичной скоростью
((sin)_max=1).
Из формулы ():
B=F_max/Il

магнитная
индукция численно равна максимальной
силе, действующей в магнитном поле на
проводник единичной длины, по которому
течет единичный ток. Таким образом,
вектор магнитной индукции – это силовая
характеристика магнитного поля.

Магнитное поле
характеризуют также с помощью
вспомогательного вектора 
вектора напряженности магнитного поля
Н:

Графически
магнитное поле изображают с помощью
линии магнитной
индукции –
это линия, в каждой точке которой вектор
магнитной индукции совпадает с
направлением касательной. Линии магнитной
индукции не следует называть силовыми
линиями, т.к. магнитная сила направлена
в каждой точке линии не по касательной,
как в случае электростатического поля,
а перпендикулярно ей. Линии магнитной
индукции 
это непрерывные замкнутые кривые, они
не имеют ни начала, ни конца, не могут
пересекаться. На рис. показаны линии
индукции поля прямого тока и поля катушки
с током.

Закон Био –
Савара – Лапласа.

Установление
основных законов электромагнетизма
произошло в очень короткий срок с 1820 г
по 1824 г. Французские ученые Био и Савар
экспериментально изучали действие
различных токов на магнитные стрелки.
Впоследствии французскому математику
Лапласу удалось обобщить их результаты
и получить выражение, которое впоследствии
получило название закон Био – Савара
– Лапласа (закон БСЛ). Кроме того, Лаплас
установил принцип независимого сложения
магнитных полей – принцип суперпозиции
магнитных полей:

Смысл принципа
суперпозиции в том, что, как и в случае
электростатических полей, магнитные
поля складываются независимо, т.е. не
влияя друг на друга.

Пользуясь
законом БСЛ и принципом суперпозиции
можно найти выражения для индукции
магнитных полей различных проводников
с током. Это сложная математическая
задача. Мы рассмотрим магнитное поле
прямого проводника с током и поле на
оси кольца с током. При этом мы будем
пренебрегать магнитным полем, которое
создают подводящие ток провода. При
выводе формул сначала надо записать
закон БСЛ для магнитной индукции поля,
создаваемого бесконечно малым элементом
с током, а затем использовать принцип
суперпозиции в интегральной форме.

Выберем
произвольную точку на расстоянии r₀
от проводника (см. рис.) и бесконечно
малый элемент проводника dl
с током I,
находящийся на расстоянии r
от нее. Вектор магнитной индукции поля
от этого элемента dB
направлен
перпендикулярно чертежу (на нас). Векторы
магнитной индукции от остальных элементов
проводника направлены также, поэтому
интегрирование будет производиться в
скалярной форме.

— — — — — — — — — — — выдано
10.03.05

(Магнитное поле
тока в подводящих проводах не учитываем).

2)Магнитное поле прямого бесконечно длинного проводника.

В случае бесконечно
длинного проводника ₁

0, ₂

180^о
(cos180^o
= 1),
получим:

3)Магнитное поле на оси кругового тока.

На рисунке
показаны линии магнитной индукции поля
кругового тока (половина поля). Это
сложное трехмерное поле, аналитической
формулы для которого не существует. Мы
получим выражение для магнитной индукции
только на
оси кольца.

Выделим на кольце
с током два элемента dl₁
и dl₂
, расположенных диаметрально противоположно
(см. рис. ниже). Магнитные индукции от
этих элементов dB₁
и dB₂
. Если разложить эти векторы на составляющие
вдоль оси х
и в перпендикулярном к ней направлении,
то перпендикулярные составляющие
взаимно компенсируются, а составляющие
по оси х будут
складываться. К этому же мы придем,
рассматривая подобные элементы по всему
кольцу. Таким образом, магнитная индукция
на оси кольца направлена вдоль оси
кольца (по правилу буравчика).

4) Магнитное поле в центре кругового тока

Это частный случай
предыдущего примера, когда х
= 0

Магнитный момент
контура с током.

Контур с током
(виток с током) при изучении магнитных
свойств вещества имеет такое же значение,
как диполь при изучении электрических
свойств вещества. Рассматривая поведение
витка с током во внешнем магнитном поле,
можно качественно объяснить намагниченность
различных веществ. Контур с током
характеризуют векторной величиной
р_магн

магнитным моментом.

Теорема о
циркуляции вектора магнитной индукции.

Так же, как
теорема Гаусса в электростатике облегчает
вычисление напряженности электростатического
поля в некоторых случаях, также теорема
о циркуляции ⁴вектора
магнитной индукции дает возможность
легко получить формулы для магнитной
индукции в некоторых простейших случаях.

Выражение ()
применяется в случаях дискретного
распределения проводников с токами,
т.е. когда имеются отдельные проводники
с токами и требуется найти индукцию В
поля вне проводников. Выражение ()
используется в случаях, когда требуется
найти индукцию В
магнитного поля внутри проводника с
током, т.е. при непрерывном распределении
тока по проводнику.

Рассмотрим
некоторые примеры применения теоремы
о циркуляции В.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Этой книги у меня нет, есть Монастырский Л.М. и др. Физика. Подготовка к ЕГЭ — 2010. Там в главе 1 «Теоретический материал для подготовки к ЕГЭ» п. 3.4 «Основные понятия и законы магнитостатики» нет ни одной формулы для расчета магнитных индукций. А задачи есть. Странно.

Решение. В основе этой задачи лежит формула для расчета магнитной индукции B₁ проводника с током I₁ длиной l₁, согнутым в виде дуги окружности радиуса r и подводящими проводами направленными строго радиально:

[ B_{1} = frac{mu _{0}}{4pi } cdot frac{I_{1} cdot l_{1}}{r^{2}}; (1)  ]

(Монастырский Л.М. считает, что эту формулу вы должны знать или уметь выводить??).

Выберем направление тока так, как указано на рис. По правилу правой руки определяем направления магнитных индукций B₁ (к нам) и B₂ (от нас.). Тогда в проекции на ось Y, направленную к нам, из принципа суперпозиции полей получаем:

B_y = B₁ – B₂. (2)

Силы тока I₁ и I₂ найдем следующим образом. Участки l₁ и l₂  соединены параллельно, следовательно:

I₁ + I₂ = I, I₁⋅R₁ = I₂⋅R₂,

где R₁ = ρ⋅l₁/S — сопротивление участка длиной l₁. Аналогично для сопротивления R₂ = ρ⋅l₂/S. Тогда

I₁⋅l₁ = I₂⋅l₂ или (это можно не делать)

[ I_{1} = I_{2} cdot frac{l_{2}}{l_{1}} ,, , ,
I_{2} cdot frac{l_{2}}{l_{1}} + I_{2} = I,, , ,
I_{2} = I cdot frac{l_{1}}{l_{1} + l_{2}} ,, , ,
I_{1} = Icdot frac{l_{2}}{l_{1} + l_{2}}.; (3) ]

После подстановки уравнений (1) и (3) в (2) получаем

[ B_{y} = frac{mu_{0}}{4 pi cdot r^{2}} cdot left(l_{1} cdot I_{1} —
l_{2} cdot I_{2} right) = 0. ]