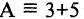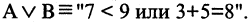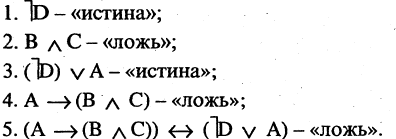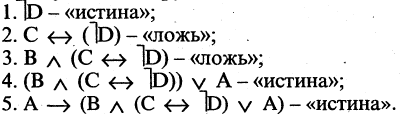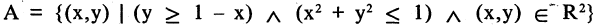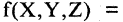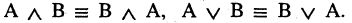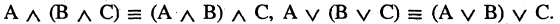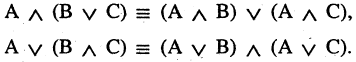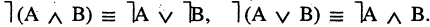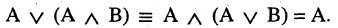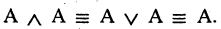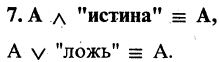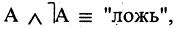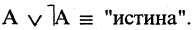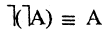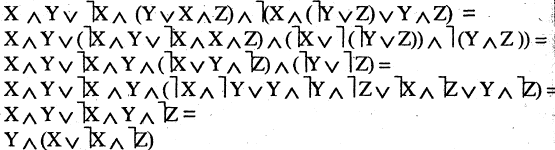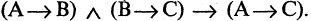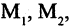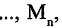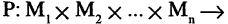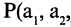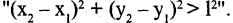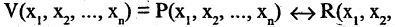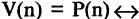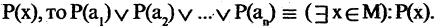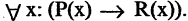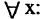В жизни мы часто слышим фразы «это не поддается логике» или «это нелогично». В целом мы понимаем, что речь идет про неверное суждение, ошибочные выводы. Но в чем конкретно нарушена логика — сказать трудно. Существуют 4 закона логики, с помощью которых можно легко отделить ложь от правды. Логика — это древняя наука, появившаяся в 4 веке до н.э., ее основателями были Аристотель, Сократ, Платон и многие другие известные философы, которые усердно изучали законы и формы правильного логического мышления. Давайте разберем на простых примерах значения основных четырех законов логики и как их применить в жизни.
Закон тождества
Любая мысль должна соответствовать самой себе, то есть иметь конкретное значение и быть точной и понятной. Самый известный пример: «ученики прослушали урок». Термин «прослушали» в этом предложение может иметь два определения: то ли ученики ничего не слушали на уроке, то ли, наоборот, внимательно изучали новую тему. Главное, на что необходимо обращать внимание, так это на неоднозначные слова, которые могут иметь несколько значений. Сложнее всего распознать нарушение тождества в сложных утверждениях:
- Что вы выберите: счастье или конфету? — Счастье.
- Как вы считаете, что лучше счастья? —Ничто!
- Но конфета лучше, чем ничто.
- Поэтому конфета получается лучше счастья.
В примере понятие «ничто» в первом варианте означало «отказ от выбора варианта», во втором, как отсутствие чего-либо.
Закон противоречия
Две отрицающих друг друга мысли не могут быть одинаково верными. Например, когда говорят «черный пес» и «белый пес», имея в виду одного и того же пса в одном промежутке времени, то правильным может быть только одно утверждение. В жизни важно выявлять противоречия, отделять игру слов от лжи.
Закон исключенного третьего
Два противоречащих утверждения не должны быть одинаково ложными. Тут важно отличать противоречащие от противоположных утверждений. Первые суждения не имеют третьего варианта, например, большая квартира и небольшая квартира. Противоположные суждения допускают, что возможен и другой вариант, например, «маленькая квартира» и «большая квартира», другой вариант — «средняя квартира». На простых примерах принцип понятен, а вот в жизни противоречащие суждения обычно разделены длинным предисловием, который сбивает с мысли.
Закон достаточного основания
Истинная мысль должна быть основана на аргументах, чтобы быть истинной. Важно, что само утверждение должно следовать из этих фактов. Например, «я готовился к экзамену, поэтому я не заслужил двойку». Один факт не подтверждает утверждение, студент мог просто прочесть лекции и не заучивать нужный материал. Данный закон помогает не делать преждевременных выводов и не верить, например, разной желтой прессе.
Проверьте себя прямо сейчас, как хорошо вы разбираетесь в логике, пройдите бесплатный онлайн-тест на логику.
Математическая логика — это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.
Алгебра высказываний
Под высказыванием понимаем всякое утверждение (повествовательное предложение), про которое всегда определенно и объективно можно сказать, является оно истинным или ложным. Например, «5-3 = 2» или «В неделе семь дней» — истинные высказывания, а «5 > 8» или «В русском языке 35 букв» — ложные высказывания. Синонимами слова «высказывания» можно считать: логическое высказывание, булевское выражение, суждение, утверждение и т.п. Фразы: «Ура!», «Который час?» — не являются высказываниями.
Если высказывание истинное, то ему предписывается значение «истина» (другие обозначения: «1», «ДА» , «И», «+», «true»). Ложному высказыванию предписывается значение «ложь» (другие обозначения: «О», «НЕТ», «Л», «-«, «false»). Совокупность возможных значений высказывания образует множество истинности {0,1} и {И,Л}.
Есть два вида высказываний: простые и составные (сложные). Под простым будем понимать высказывание, которое не может быть разбито на более простые высказывания. Про него всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой. Из простых высказываний при помощи логических операций можно строить сложные высказывания, которые всегда только истинны или только ложные. Высказывания обозначаются заглавными латинскими буквами: 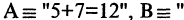
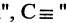
Логические операции
Операции над высказываниями задают в виде таблиц, называемых таблицами истинности.
Отрицание высказывания
Для каждого высказывания А может быть сформировано новое высказывание 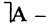
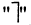
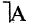
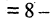
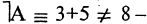
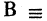
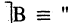
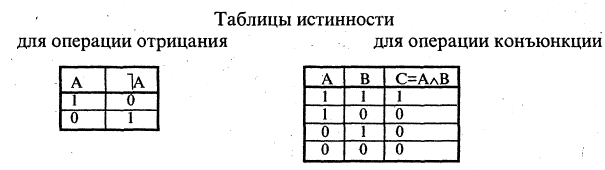
Конъюнкция высказываний
Конъюнкцией высказываний А и В называется высказывание 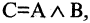

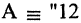
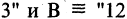

Операцию конъюнкции можно определить и для нескольких высказываний как связку высказываний, объединенных союзом «и». Конъюнкция из п высказываний — новое высказывание, причем высказывание
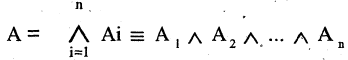
имеет значение «истина», если 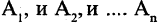
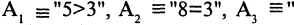
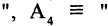
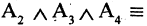
Мурманск севернее Смоленска») — ложное высказывание. В то время как 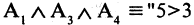
Дизъюнкция высказываний
Дизъюнкцией высказываний А и В называется высказывание 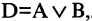

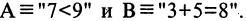
Операцию дизъюнкции можно определить для нескольких высказываний как связку высказываний, объединенных союзом «или»,
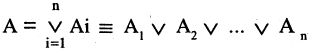
В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.
Импликация высказываний
Импликацией высказываний А и В называется высказывание 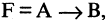
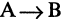
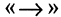


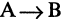

Пусть А и В истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием. Когда же папа не купит сыну велосипед (В — ложно), получив премию (А — истинно), то это, мягко говоря, не логичный поступок, а импликация имеет значение «ложь». Если же папа не получит премию (А — ложно), но купит велосипед (В -истинно), то результат положителен. В том случае, если, не получив премии (А ложно), папа не купит велосипед (В — ложно) -обещание не нарушено, результат можно считать истинным.
Эквивалентность высказываний
Эквивалентностью высказываний А и В называется высказывание 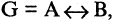
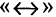






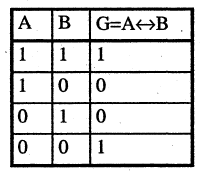
Замечание. Характерной особенностью операций над высказываниями является введение логических союзов с точно определенным смыслом, не допускающим никакой двусмысленности в толковании этих символов. Таким образом, математическая логика применима не для любых высказываний, а только для таких, которые допуск кают четкую оценку в двоичной системе «истина — ложь». Для преодоления такого рода ограничений в рамках нечеткой математики разрабатывается нечеткая логика.
Если в выражении встречаются различные логические операции, то в качестве естественного порядка (выполняемого поочередно слева направо) используется следующая последовательность: 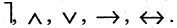
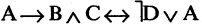
Введя скобки, получим формулу 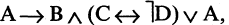
Если в выражении присутствуют арифметические операции, операции сравнения и логические операции, то порядок старшинства операций следующий:
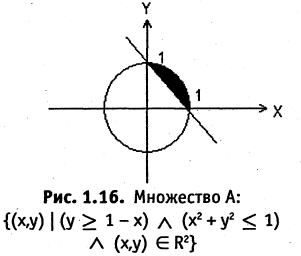
Использование различных операций позволяет в удобной аналитической форме задавать различные множества.
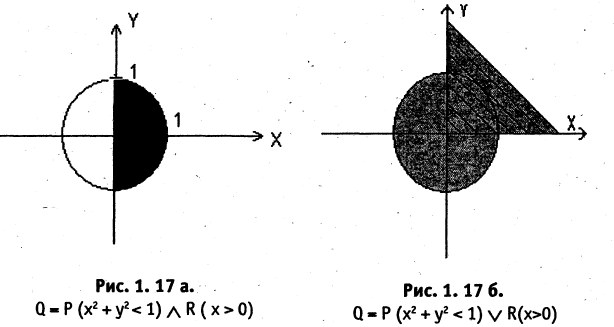
Например, множество точек А, заштрихованное на рис. 1.16, может быть задано следующей формулой:
Система операций 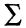
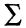
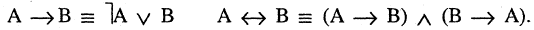
Булевы функции
Всякую формулу логики высказываний можно рассматривать как некоторую функцию: каждая буква (высказывание) может принимать одно из двух значений — «истина» или «ложь», при этом сложное высказывание, заданное этой формулой, также может быть истинным или ложным. Так формула
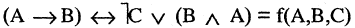
выражает функцию от переменных А, В и С.
Такого рода функции называются булевыми, а их аргументы — булевыми переменными. Аргументы булевых функций могут представлять собой, сокращенные обозначения некоторых конкретных высказываний. Тогда функция обозначает сокращенную запись некоторого сложного высказывания. Например, 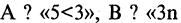
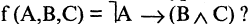
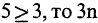
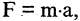
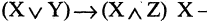
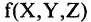
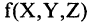
Целый ряд булевых функций обладает тем свойством, что они принимают одни и те же значения при любых значениях истинности аргументов. Такие формулы называются тождественно истинными. Например, при любых X и Y истинны формулы 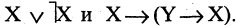
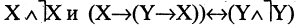
Наиболее важные тождественно истинные формулы получили название Основные законы математической логики.
Основные законы математической логики
1.Коммутативность
2.Ассоциативность
3.Дистрибутивность
4.Законы де Моргана
5.Закон поглощения
6.Закон идемпотентности
8.Закон противоречия
9.Закон исключения третьего
10.Закон двойного отрицания
Пример:
Упростить выражение, используя тождественны преобразования
Существует бесконечное множество тавтологий. Некоторы из них легли в основу методов доказательства.
Основные методы доказательств
При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.
Формально каждая теорема может быть выражена в форме импликации 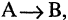
Метод цепочек импликаций
Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из 
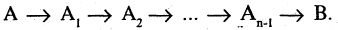
В основе этого метода лежит закон цепного высказывания или закон силлогизма
Метод от противного
Метод от противного. Используя этот метод, вместо доказательства прямого следствия «из А следует В» доказывают, что из «не В» следует «не А». Этот метод основан на законе контрапозиций, имеющем следующий вид:
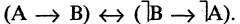
Метод необходимого и достаточного
Метод необходимого и достаточного. Теорема формулируется так: «Чтобы имело место А, необходимо и достаточно выполнение В». Доказательство такого вида теоремы распадается на две части:
а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);
б) если имеет место В, то имеет место и А (В достаточно для А).
Доказательство таким методом базируется на законе тавтологии:
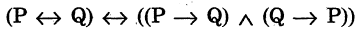
Алгебра предикатов
Предикатом 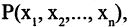
называется функция Р, отображающая их прямое произведение на двоичное множество, т. е. 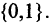
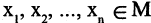
Рассмотрим примеры, 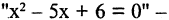
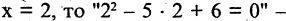
положив 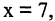
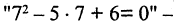
Всякий предикат 
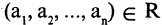
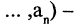

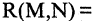
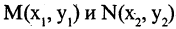
Если в 
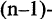
Логические операции над предикатами
Отрицание предиката
Пусть предикат 
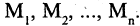


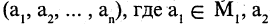
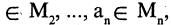
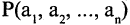
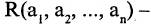
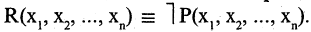
Например, предикат «

Конъюнкция предикатов
Пусть на множествах 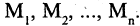

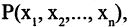

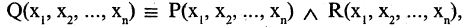
который истинен для одних и тех же кортежей только тогда, когда оба предиката — и 
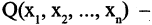
Например, конъюнкция предикатов 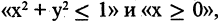
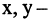
Дизъюнкция предикатов
Дизъюнкция предикатов 


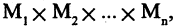


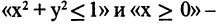
Импликация предикатов
Импликация предикатов 

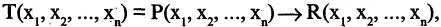
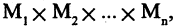


Например, импликация «



Эквивалентность предикатов
Эквивалентность предикатов 

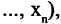



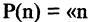
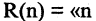

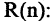


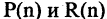
Наряду с логическими операциями важную роль играют операции, называемые кванторами. Квантор всеобщности есть операция, которая предикат 


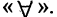



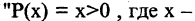



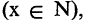

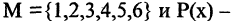

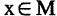
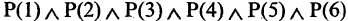
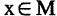
Квантор существования
Квантор существования есть операция, которая предикат 
из М, обладающий свойством 
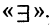







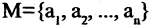
Кванторы обладают свойствами, являющимися аналогами законов де Моргана:
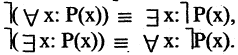
С помощью кванторов можно выражать ряд часто используемых на практике отношений между множествами. Например, высказывание «все объекты 

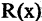
Переход от 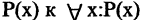



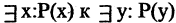
Рассмотрим пример. На множестве чисел задан двухместный предикат 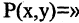


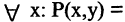

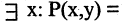

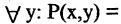

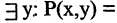

Связывая обе переменные данного предиката, получим высказывания:
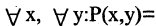
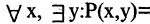
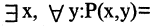
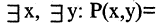
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Парадокс лжеца — семейство логических парадоксов, смысл коих при удалении разнообразия формулировок можно заключить в утверждении: «Я лгу» или «Данное утверждение ложно». Если предположить, что утверждение истинно, то, поскольку оно гласит свою ложность, оно ложно, что является противоречием. Напротив, если предположить его ложность, то оно соответствует тому, что само гласит, а потому истинно, что также является противоречием. Парадокс образуется благодаря указанию предложения на самого себя с соответствующим отрицанием (самореференции).
Первоначальная формулировка[]
Формулировка Эпименида.[]
Самое ранняя формулировка, приписываемая полумифическому критскому философу Эпименида: просто (Говорит Эпиминид. Эпиминид — критянин) «Все критяне лжецы» или «Все критяне лжецы. Я критянин», датирующаяся VII в. до н.э.
Вероятно, именно эта формулировка парадокса лжеца даётся в Новом Завете у апостола Павла в Тит. 1:12-13: «Из них же самих один стихотворец сказал: «Критяне всегда лжецы, злые звери, утробы ленивые». Свидетельство это справедливо….»
Формулировка Евбулида.[]
Сам парадокс лжеца был известен в Древней Греции IV века до н. э. Евбулид Милетский включил его в список своих семи софизмов в следующей формулировке: «Человек говорит, что он лжёт. То, что он говорит — истина или ложь?». Является возможной первоначальной формулировкой.
Подсемейства[]
Классический парадокс[]
Рассмотрим следующее утверждение: «А: Утверждение А ложно»
Если утверждение истинно, то утверждение ложно, противоречие. Если же оно ложно, то утверждение не ложно, а значит истинно, противоречие. Последний шаг опирается на закон исключённого третьего, гласящий, что любое логическое утверждение или истинно, или ложно. Естественное решение — отрицание закона исключённого третьего — не работает в других вариантах парадокса лжеца.
Закон исключённого третьего[]
Рассмотрим следующее утверждение: «А: Утверждение А не является истинным»
Если утверждение истинно, то утверждение не истинно, противоречие. Если же оно не истинно, то утверждение истинно, противоречие. Такой вариант не использует закон исключённого третьего, тем не менее, утверждение ссылается само на себя.
Другая формулировка предполагает, что третий вариант, отличный от истинности или ложности — это бессмысленность: «А: Утверждение А ложно или бессмысленно»
Логический цикл[]
Здесь приведена фреска работы Рафаэля: «Афинская школа». В центре картины Аристотель и Платон ведут спор: Платон указывает пальцем на небо, приводя свой мир идеальных идей, а Аристотель, эмпирист, на землю, приводя первенство опыта и познания реального. Но можно представить иной спор: Платон: Следующее высказывание Аристотеля будет ложно. Аристотель: Ты прав, учитель. Возникает парадокс лжеца вида Логического цикла.
Рассмотрим следующие утверждения:
А: Утверждение Б ложно.
Б: Утверждение А истинно.
Если истинно, то ложно и не истинно, противоречие. Если ложно, то не ложно и истинно, противоречие. Исправление ложности на неистинность и исправляет необходимость закона исключённого третьего аналогично предыдущему примеру. Такой вариант не использует отсылки утверждения к самому себе, но использует отсылку к полностью взаимосвязанной смысловой системе.
Возможны и циклы большей длины, например, такой:
А: Утверждение Б ложно.
Б: Утверждение В ложно.
В: Утверждение А ложно.
Парадокс Карри (Доказательство Санто-Клауса)[]
Сначала рассмотрим утверждение: «А: Если утверждение А (можно заменить на это утверждение) является истинным, 1 равен 0, если утверждение А является ложным, 1 не равен 0»
В таком случае, если А истинно, 1=0 истинно, что невозможно. Значит истинность утверждения А невозможна»
Дед Мороз разбирается с парадоксом Карри, дабы понять, почему он существует
Если А ложно, то 1 не = 0. Но, одновременно, 1=0, ибо утверждение А ложно, а значит, по правилу исключённого третьего, истина такова: «А: Если утверждение А является истинным, 1 не равно 0, если утверждение А является ложным, 1 равно 0». Из этого следует, что а) мы получили классический парадокс лжеца (Ибо тогда утверждение истинно, так как 1 не может быть равен 0. Но если оно истинно, то 1=0 и т.д.), б) независимо от истинности или ложности утверждения, 1=0.
Тогда уже ничего не стоит заменить 1=0 на факт существования Санта-Клауса, русалок или Деда Мороза, а указание А на себя, на «это предложение», получив классическую формулировку парадокса Карри: «Если это предложение является истинным, то Санта Клаус существует» или, при желании, заменив Санта-Клауса Карри на нечто другое, «Если это предложение является истинным, то русалки существуют», или «Если это предложение является истинным, то Дед Мороз существует». Очень наглядное применение парадокса Карри: «Если это утверждение является истинным, то чайник, вращающийся вокруг солнца по эллиптической орбите между Марсом и Землёй» или, ещё наглядней, «Если это утверждение является истинным, то Бог существует» ,что и сделал Буридан, соединив форму Карри с формой Логического Цикла (см. ниже).
Парадокс Пиноккио[]
Данное семейство парадоксов лжеца не представляет из себя особого интереса — вся суть такового заключается в переносе парадокса на какой-либо материальный предмет (группу предметов, систему и т.д.), состояние коего/коих зависит от ложности или истинности некого утверждения. Классическим пример:
«У Пиноккио имелось свойство: когда он лгал, его нос тут же заметно увеличивался. Что будет, если Пиноккио скажет: «Сейчас у меня удлинится нос»? Если нос не увеличится — значит, мальчик соврал, и нос будет обязан тут же вырасти. А если нос вырастет — значит, мальчик сказал правду, но тогда почему вырос нос?»
Парадокс Ябло[]
Возьмём бесконечное число утверждений:
- (S1): для всех k > 1, Sk есть ложь
- (S2): для всех k > 2, Sk есть ложь
- (S3): для всех k > 3, Sk есть ложь
- …
- …
В частности, следует обратить особое внимание на тот факт, что каждое утверждение ничего не говорит о своей собственной истинности или ложности, даже косвенным способом, так как оно утверждает что-то лишь об утверждениях с большими номерами, и для всех них это тоже верно.
Возьмём любое утверждение Sk. Ложно оно или истинно? Предположим, что истинно. Тогда Sk+1, Sk+2 и т.д. все ложны. Но ложность Sk+2, Sk+3, и т.д. — как раз то, что утверждает Sk+1. Поэтому получаем противоречие: с одной стороны Sk+1 ложно (прямое следствие истинности Sk), с другой стороны истинно (прямо следствие ложности Sk+2, Sk+3, Sk+n). Раз мы достигли противоречия, значит, наше предположение было неверным, и Sk на самом деле ложно. Это верно для любого k.
Известные частные случаи[]
Исторические случаи[]
Здесь находятся известные исторические случаи формулировок Парадокса Лжеца, относящиеся к той или иной описанной или неописанной выше подсемейств. В случае отношения частного случая к описываемому подсемейству, за исключением особенных случаев, описание логической цепочки парадокса смысла приводить нет и потому таковой приводится не будет.
Сократа обвинили софисты в порче молодежи и отрицании богов, из-за составленной им конкуренции и не согласности его с их принципами. Фактически, как сказал Бертран Рассел, в то время софисты были как поганые адвокаты — никому неприятны и всем нужны. Платон присутствовал на суде, но не был в момент казни — возможно ли что между ними был описанный здесь спор?
Спор Сократа и Платона.[]
В средневековье была известен такой Логический Цикл, являющийся, возможно, отцом данного подсемейства и его классической иллюстрацией:
«Платон: Следующие утверждение Сократа будет ложным.
Сократ: То, что сказал Платон, истинно.»
Доказательство Жака Буридана.[]
Богослов Жак Буридан использовал парадокс для доказательства Бога: «Бог существует. Ни одно из этих двух утверждений не является истинным.» Если первое утверждение ложно, то второе превращается в привычный парадокс Лжеца — значит, дабы избежать парадокса, надо признать истинность первого утверждения и, соответственно, ложность второго. Но подобные изыскания, конечно, легко опровергаются — Бога в первом утверждении легко и без изменения смысла можно заменить на Чайник Рассела, русалок, Деда Мороза, Санта-Клауса и/или совершенных Голубей с лазерными глазами и бутербродами вместо ног. Фактически, Буридан использовал парадокс Карри (см. выше) в форме логического цикла.
Двойной Лжец (Картонка Джордана).[]
Эта версия парадокса Лжеца была представлена английским математиком Филиппом Эдвардом Бертраном Джорданом в 1913 году. Лжец Джордана относиться к подсемейству Логических Циклов, являясь почти что полной копией «Спора Сократа и Платона»:
«Следующее написано на обоих сторонах карточки:
На обратной стороне: «Утверждение на другой стороне этой карточки верно»
На лицевой стороне: «Утверждение на другой стороне этой карточки неверно»»
Прочие представители[]
Здесь приведены всевозможные исторически невесомые и/или придуманные Вами представители этого семейства. В случае, оригинального по Вашему мнению парадокса просим отнести таковой в отдельную статью. Итак,
Чтимое, писанное и услышанное[]
Данные парадоксы повторяют Классический Парадокс Лжеца, но ссылаются лишь на частный способ выражения мыслей, как, например, чтение и слух:
«Всё написанное — ложь», написанное где-либо.
«Всё Вами наблюдаемое — ложь»/»Всё прочитанное — ложь»
«Всё сказанное — ложь», произнесённое.
Данный ряд можно бесконечно долго продолжать, сделав средства выражения ещё более ограниченными и/или реже используемыми, продолжая добавлять:
«Все фразы на русском языке — ложь»,
«•−− ••• • •−•−•− −−•• •− −•− −−− −•• •• •−• −−− •−− •− −• −• −−− • −• •− −− −−− •−• −−•• •−•− −• −•− • −••••− •−•• −−− •••− −••− ••••••»,
«Все сказанное на Тоттепедии — ложь»,
«Всё в этой статье — ложь», и т.д.
Попытки решения, исследования и комментарии[]
Исторические[]
Диодор Кронос
Последователь Аристотеля Теофраст написал о парадоксе три папируса, а ранний стоик Хрисипп — шесть, но до нас они не дошли.
Известны две смерти мыслителей, вызванных попытками решить этот парадокс. Логик Диодор Кронос опрометчиво дал обет воздержания от еды до решения парадокса — и вскоре умер от истощения. Учёный, грамматик и поэт. Филит Косский, отчаявшись найти решение, либо покончил с собой, либо, будучи слабого здоровья, умер от недоедания и бессонницы, слишком увлёкшись проблемой. Надпись на могиле Филита на острове Кос гласит:
«О странник! Я Филит Косский,
И это лжец привёл к моей смерти,
И бессонные ночи из-за него»
Аристотель предлагал вариант своего решения. Он указывал, что софистические доводы («О софистических опровержениях», гл. 25) основаны на том, что «о чем-то [присущем] в собственном смысле утверждают как [о присущем] в каком-то отношении, или где-то, или каким-то образом, или в отношении чего-то, но не вообще» (Arist. Soph. El. 081а 25)[. Поэтому в варианте «человек говорит, что он лжёт» вполне верно рассуждение: «Однако, ничто не мешает, чтобы один и тот же вообще-то говорил неправду, а в каком-то отношении и о чем-то говорил правду или чтобы в чем-то он был правдив, а вообще-то неправдив» (Arist. Soph. El. 180b 5). Таким образом разделяются лжец как «некто, кто часто лжёт» и «тот, кто лжёт в определённый момент». Но таким образом Аристотель по сути ограничился указанием на причину возникновения парадоксальности, и вариант парадокса в прямом виде «это предложение ложно» таким образом не решается и не «обходится»].
Фрэнк Рамсей парадокс лжеца (в виде «Я сейчас лгу») рассматривал как лингвистический, относил к классу семантических, а не теоретико-множественных:
«…противоречия группы В не являются чисто логическими и не могут быть сформулированы в одних логических терминах, ибо все они содержат некоторую отсылку к мысли, языку или символизму, которые являются не формальными, но эмпирическими терминами. Поэтому своим возникновением они могут быть обязаны не ошибочной логике или математике, но ошибочным идеям, касающимся мысли и языка.»
Ряд других авторов часто пытаются решить парадокс именно логико-математическими средствами. Альфред Тарский пытался с помощью своей логико-математической теории переформулировать парадокс с бытового языка на некий формальный язык, имеющий однозначную логическую структуру. Формально можно сказать, что А. Тарский нашёл решение: предикаты «истинно» либо «ложно» он считает терминами метаязыка и их нельзя применять к языку, на котором сформулировано изначальное высказывание. Однако это рассуждение основано на концепции метаязыка, а парадокс «внутри» обычного языка остаётся нерешённым.
К теме «перевода» парадокса на формальный логический язык имеет отношение и первая теорема Гёделя о неполноте:
«Факт, что теорема Гёделя и парадокс Лжеца близко соотносятся, не только хорошо известен, но является даже общим представлением логического сообщества. …сам Гёдель не стал исключением, сделав замечание в статье, анонсируя свой результат. «Аналогия между этим результатом и антиномией Ришара бросается в глаза; есть также близкое родство с антиномией „Лжеца“. здесь мы сталкиваемся с предложением, которое утверждает свою собственную недоказуемость»»
Г. Серени указывает, что эта связь является общепризнанной в среде специалистов, но имеет форму скорее аналогии, внешнего сходства, и существует мало исследований о точной природе этой связи. Ван Хейеноорт указывает, что если перейти от понятия истинности к доказательству, то парадокс исчезает:
«…предложение, утверждающее «Я не истинно»… получаем парадокс… Но если мы как-то сконструируем предложение «Я не доказуемо», парадокс не возникает. Обозначим через g предложение, и в отношении понятия «доказательства» просто предположим, что ничто из доказуемого не может быть ложным. Если бы g было доказуемым, оно было бы ложным, отсюда, оно не доказуемо. Следовательно, оно не доказуемо и истинно (поскольку это именно то, что оно утверждает). Отрицание g, которое устанавливает, что оно доказуемо, ложно, отсюда оно также не доказуемо. Мы скользим вдоль парадокса, никогда не впадая в него истинно. Предложение g недоказуемо и истинно; его отрицание недоказуемо и ложно. Единственное обстоятельство, которое приводит к этому удивительному результату, это введение различия между «истинно» и «доказуемо»»
Проблемы логики, связанные с парадоксом, менялись в зависимости от концепции рассмотрения: является ли он двусмысленностью или же бессмысленностью, или — примером смешения разговорного языка и логического метаязыка, которые в повседневности не разделяются. Если же их дифференцировать, то утверждение «Я лгу» сформулировать невозможно. Вполне возможно, что в будущем этот давний парадокс приведёт к обнаружению других проблем в соответствующей области.
Между тем имеются и попытки отказаться от восприятия парадокса, сделать вид, что его нет. Вдовиченко А.В. предлагает рассмотреть парадокс «как естественный вербальный материал», указывая, что высказывающий этот парадокс «мог вовсе не думать о себе, когда произносил свои слова», т.е. не причислять себя к «критянам», хотя им и являлся (речь именно к «критянской» формулировке): «мог говорить аффективно, имея в ввиду лишь своё отношение к ним, не причисляя к ним себя»
Неисторические[]
Решения характера позитивизма:[]
Пример иррациональной идеи
Можно сказать, что все понятия, касающиеся не представляемых объектов и идей, невозможных к представлению, являются иррациональными. Самый явный тому пример — идея не представляемой (ненаблюдаемой) бесконечности, невозможной к представлению, бесконечности и вытекающие из неё нерешаемые задачи, вроде бесконечность -/+ 1, решения коих так же иррациональны. Значит, парадокс лжеца, ссылаемый сам на себя, используя самореференцию, являясь тем самым не представляемым «рекурсивным» утверждением, является иррациональной идеей. А значит, и все решения его будут иррациональны и бессмысленны, подобно решению задачи о вливании молока в термос, наполненного бесконечным количеством молока. Далее же, согласно заветам логического позитивизма, мы должны просто избавится от его решения.
Ссылки[]
Про парадокс Лжеца Вы можете прочитать на Википедии, откуда частично взята данная статья.
На уроке рассмотрен материал для подготовки к огэ по информатике, решение задания 3
3-е задание: «Значение логического выражения»
Уровень сложности — базовый,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
* до 2020 г — это задание № 2 ОГЭ
Содержание:
- Объяснение 3 задания ОГЭ по информатике
- ОГЭ информатика разбор задания 3
- Актуальное
- Тренировочные
- Для подготовки к решению 3 задания ОГЭ по информатике следует вспомнить знаки сравнения. В логических выражениях используются следующие знаки сравнения:
- В логических выражениях участвуют всего два значения выражений: ИСТИНА и ЛОЖЬ.
- Рассмотрим результат выполнения логических выражений для двух высказываний — А и Б:
- Если отрицание НЕ стоит перед скобкой с выражением, то НЕ ставится перед каждой частью выражения в скобках и при этом операция внутри скобок меняется:
|
> |
больше |
|
< |
меньше |
|
= |
равно |
|
≥ |
больше или равно |
|
≤ |
меньше или равно |
| 1 | А ИЛИ Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | если А=истина И Б=ложь | |
| 3 | если А=ложь И Б=истина | |
| 4 | А ИЛИ Б = ЛОЖЬ → | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией ИЛИ легче проверить «на ложь»:
с операцией ИЛИ результатом будет ЛОЖЬ только в одном единственном случае, — когда оба выражения — А и Б — ложны
| 1 | А И Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | А И Б = ЛОЖЬ → | если А=истина И Б=ложь |
| 3 | если А=ложь И Б=истина | |
| 4 | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией И легче проверить «на истинность»:
с операцией И результатом будет ИСТИНА только в одном единственном случае, — когда оба выражения — А и Б — истинны
| Исходные значения | Результат | |
|---|---|---|
| 1 | НЕ А если А=истина |
А = ЛОЖЬ |
| НЕ(5 > 0) | 5 ≤ 0 | |
| 2 | НЕ А если А=ложь |
А = ИСТИНА |
| НЕ(-2 > 0) | -2 ≤ 0 | |
| 3 | НЕ (НЕ А) | = А |
| 1 | НЕ |
| 2 | выражение в скобках |
| 3 | И |
| 4 | ИЛИ |
| 1 | НЕ (А ИЛИ Б) | НЕ А И НЕ Б |
| 2 | НЕ (А И Б) | НЕ А ИЛИ НЕ Б |
ОГЭ информатика разбор задания 3
Подробный видеоразбор по ОГЭ 3 задания:
📹 Видеорешение на RuTube здесь
Актуальное
Значение логического выражения
Разбор задания 3.7. Демонстрационный вариант ОГЭ 2022 г ФИПИ:
Напишите наименьшее число x, для которого истинно высказывание:
(x > 16) И НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x > 16) И (x чётное)
(x > 16) И (x чётное) = ИСТИНА истина истина
Ответ: 18
Разбор задания 3.12:
Напишите наименьшее число x, для которого ложно высказывание:
(x ≤ 15) ИЛИ НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x ≤ 15) ИЛИ (x чётное) = 0 (ложь)
(x ≤ 15) ИЛИ (x чётное) = ЛОЖЬ ложь ложь
Ответ: 17
Тренировочные
Разбор задания 3.1:
Для какого из приведённых значений числа X ложно высказывание:
НЕ (X < 6) ИЛИ (X < 5) ?
1) 7
2) 6
3) 5
4) 4
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 6) (X < 6) - ложь, значит результат: X ≥ 6
(X ≥ 6) ИЛИ (X < 5)
(X ≥ 6) ИЛИ (X < 5) = ЛОЖЬ ложь ложь
1. (X ≥ 6) = ЛОЖЬ => X < 6 2. (X < 5) = ЛОЖЬ => X ≥ 5
5 < 6 и 5 ≥ 5
Ответ: 3
Разбор задания 3.2:
Для какого из приведённых значений числа X истинно высказывание:
(X < 8) И НЕ (X < 7) ?
1) 9
2) 8
3) 7
4) 6
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 7) (X < 7) - ложь, значит результат: X ≥ 7
(X < 8) И (X ≥ 7)
(X < 8) И (X ≥ 7) = ИСТИНА истина истина
1. (X < 8) = ИСТИНА => X < 8 2. (X ≥ 7) = ИСТИНА => X ≥ 7
7 < 8 и 7 ≥ 7
Ответ: 3
Разбор задания 3.3:
Для какого из приведённых имён ЛОЖНО высказывание:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) ?
1) Анна
2) Елена
3) Павел
4) Егор
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) = = (НЕ(Третья буква согласная) ИЛИ НЕ(Последняя буква гласная))
1. НЕ(Третья буква согласная) => Третья буква НЕ согласная 2. НЕ(Последняя буква гласная) => Последняя буква НЕ гласная
(Третья буква не согласная) ИЛИ (Последняя буква не гласная)
(Третья буква не согласная) ИЛИ (Последняя буква не гласная) = ЛОЖЬ
ложь ложь
1. (Третья буква не согласная) = ЛОЖЬ => Третья буква согласная 2. (Последняя буква не гласная) = ЛОЖЬ => Последняя буква гласная
Третья буква "н" согласная и Последняя буква "а" гласная
Ответ: 1
Разбор задания 3.4:
Для какого из приведённых имён ИСТИННО высказывание:
НЕ ((число > 50) ИЛИ НЕ(число четное)) ?
1) 43
2) 50
3) 61
4) 72
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ в малых скобках:
НЕ(число четное) => число нечетное
НЕ ((число > 50) ИЛИ (число нечетное)) = = (НЕ(число > 50) И НЕ(число нечетное))
1. НЕ(число > 50) => число <= 50 2. НЕ(число нечетное) => число четное
(число <= 50) И (число четное)
(число <= 50) И (число нечетное) = ИСТИНА
истина истина
Ответ: 2
Разбор задания 3.5.:
Для какого из приведённых слов ЛОЖНО высказывание:
(последняя буква согласная) ИЛИ НЕ ((первая буква согласная) И (вторая буква гласная)) ?
1) Тигр
2) Выдра
3) Енот
4) Краб
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((первая буква согласная) И (вторая буква гласная)) = = (НЕ(первая буква гласная) ИЛИ НЕ(вторая буква гласная))
1. НЕ(первая буква согласная) => первая буква гласная 2. НЕ(вторая буква гласная) => вторая буква согласная
(первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква согласная) ИЛИ
ложь ложь
(вторая буква согласная) = ЛОЖЬ
ложь
1. (последняя буква согласная) = ЛОЖЬ => последняя буква гласная 2. (первая буква гласная) = ЛОЖЬ => первая буква согласная 3. (вторая буква согласная) = ЛОЖЬ => вторая буква гласная
Ответ: 2
Разбор задания 3.6:
Для какого из приведённых слов верно высказывание:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) ?
1) АИДА
2) СЕРГЕЙ
3) СТЕПАН
4) АРТЕМ
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении находятся большие скобки, с которых необходимо начать решение.
- Внешняя операция, т.е. последняя по приоритету — это операция И. Рассмотрим ее подробней, разделив общее высказывание на две части относительно этой операции:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная))
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) истина истина
((последняя буква согласная) ИЛИ (вторая буква согласная))
истина ИЛИ истина
(первая буква гласная) И (или первая или вторая буква в слове согласная) истина истина
Ответ: 4
Осуществление поиска в готовой базе данных по сформулированному условию
* до 2020 г — это задание № 12 ОГЭ
Разбор задания 3.8:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Рига | скорый | 15:45 | Рижский |
| Ростов | фирменный | 17:36 | Казанский |
| Самара | фирменный | 14:20 | Казанский |
| Самара | скорый | 17:40 | Казанский |
| Самара | скорый | 15:56 | Казанский |
| Самара | скорый | 15:56 | Павелецкий |
| Самара | фирменный | 23:14 | Курский |
| Санкт-Петербург | скорый | 8:00 | Ленинградский |
| Санкт-Петербург | скорый | 4:00 | Ленинградский |
| Саратов | скорый | 14:57 | Павелецкий |
| Саратов | пассажирский | 15:58 | Павелецкий |
| Саратов | скорый | 15:30 | Павелецкий |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») ИЛИ (Вокзал = «Павелецкий»)?
✍ Решение:
- В условии находится логическая операция ИЛИ, которая истинна тогда, кода хоть одно из логических выражений истинно. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
1. Категория поезда = «скорый» и Вокзал = любой 2. Категория поезда = «скорый» и Вокзал = «Павелецкий» 3. Категория поезда = любой и Вокзал = «Павелецкий»
Ответ: 9
Разбор задания 3.9:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») И (Время в пути > 40:00)?
✍ Решение:
- В условии находится логическая операция И, которая истинна только тогда, кода оба (все) выражения истинны. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
Категория поезда = «скорый» и Время в пути > 40:00 одновременно
Ответ: 3
Разбор задания 3.10:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Пункт назначения = «Волгоград») ИЛИ (Категория поезда = «пассажирский») И (Время в пути < 50:00)?
В ответе укажите одно число — искомое количество записей.
✍ Решение:
- В условии находятся две логических операции: И и ИЛИ. Первой всегда выполняется операция И, затем добавляются записи для операции ИЛИ.
- Операция И истинна только тогда, кода оба (все) выражения истинны.
(Категория поезда = «пассажирский») И (Время в пути < 50:00) одновременно
(Пункт назначения = «Волгоград») добавить к предыдущему результату
Ответ: 4
Разбор задания 3.11:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Махачкала | скорый | 39.25 | Павелецкий |
| Махачкала | скорый | 53.53 | Курский |
| Мурманск | скорый | 35.32 | Ленинградский |
| Мурманск | скорый | 32.50 | Ленинградский |
| Мурманск | пассажирский | 37.52 | Ленинградский |
| Мурманск | пассажирский | 37.16 | Ленинградский |
| Назрань | пассажирский | 40.23 | Павелецкий |
| Нальчик | скорый | 34.55 | Казанский |
| Нерюигри | скорый | 125.41 | Казанский |
| Новосибирск | скорый | 47.30 | Ярославский |
| Нижневартовск | скорый | 52.33 | Казанский |
| Нижний Тагил | фирменный | 31.36 | Ярославский |
Сколько записей в данном фрагменте удовлетворяют условию:
НЕ (Вокзал = «Ленинградский») И (Время в пути > 50.00)?
✍ Решение:
- В условии находятся две логических операции: НЕ и И.
- Первой всегда выполняется операция НЕ, затем добавляются записи для операции И.
- Операция НЕ обозначает обратное высказывание:
НЕ(Вокзал = «Ленинградский»)
то же самое, что
(Вокзал ≠ «Ленинградский»)
(Вокзал ≠ «Ленинградский») И (Время в пути > 50.00) одновременно
Ответ: 3
Как распознать ложные аргументы и не попасться на крючок
Отрывок из книги Тома Чатфилда «Критическое мышление», которая учит анализировать, сомневаться и формировать собственное мнение.
Что такое аргумент
Почему важно уметь мыслить логически? Прежде чем ответить на этот вопрос, разберёмся с другим понятием — утверждением. Вот, например, утверждение относительно практики содержания животных в качестве домашних питомцев:
Держать животных дома неправильно.
Утверждение — это изложение факта или убеждения, не подкреплённое обоснованием или доказательством. Само по себе оно не более чем передаваемая информация. Напротив, аргумент — нечто более ценное.
Рассмотрим следующую аргументацию против содержания домашних питомцев:
Животных нельзя превращать в домашних питомцев, поскольку это лишает их свободы и возможности вести достойную жизнь. Все живые существа достойны свободы.
На сей раз перед нами не только заявление о том, какой ситуация видится говорящему, но и логическая цепочка, призванная его обосновать. Попытка дать заключению логическое обоснование очень важна.
Когда некто утверждает, что «держать животных дома неправильно», нам неоткуда узнать, почему он так считает. Возможно, у него есть для этого настолько убедительная причина, что наша жизнь изменится, едва лишь мы её услышим. Или он просто повторяет слова своей матери? Мы не знаем. Как только этот человек начинает аргументировать свою позицию, перед нами открываются очень интересные возможности. Мы можем:
- лучше понять его взгляд на ситуацию;
- осознать, согласны мы с его логикой или нет;
- сравнить аргументы и узнать, нет ли более убедительных в поддержку другой точки зрения;
- выяснить, не упускает ли говорящий важные данные или идеи;
- поспорить с ним и попытаться его переубедить — или изменить собственную точку зрения.
Приводя аргументы, другие люди побуждают вас согласиться с определённым умозаключением и с этой целью демонстрируют последовательность предположений, которые (на их взгляд) его поддерживают. Отсюда вытекает рабочее определение аргумента в контексте критического мышления.
Аргумент — это попытка убеждения в истинности вывода посредством логики.
Можно выделить два ключевых элемента:
- вам предлагают логическую цепочку, которая…
- …призвана заставить вас принять вывод.
Вывод — это итог аргументации, финиш, к которому подводило всё прочее. Вывод из одного аргумента способен стать отправной точкой для другого, но из каждого отдельного аргумента может быть лишь один окончательный вывод. […]
Какими бывают ложные аргументы
Посмотрите, как работает ложный аргумент. Вы заметили, что здесь не так?
Все, с кем я разговаривал, считают, что президент прекрасно справляется со своими обязанностями. Хватит ворчать, пора уже признать, что это вполне подходящий лидер для нашей страны!
Даже если вы инстинктивно чувствуете, что с этой цепочкой рассуждений не всё благополучно, обнаружить дефект трудно, поскольку он является имплицитным. Здесь присутствует неозвученная предпосылка, и загвоздка именно в ней — в том, что не было сказано или признано открыто. Если вписать эту предпосылку, проблема становится очевидной.
Все, с кем я разговаривал, считают, что президент прекрасно справляется со своими обязанностями. Коллективного мнения опрошенных мной людей достаточно для доказательства истины. Хватит уже ворчать, пора признать, что это вполне подходящий лидер для нашей страны!
Обратите внимание, невысказанная предпосылка — что мнения большинства достаточно для признания истинности — является общей, а не частной. Эта разновидность ложного аргумента называется апеллированием к популярности. Как только мы её обнаружили, становится очевидным, что это недостаточное основание для вывода (если только не доказано, что говорящий тщательным образом опросил огромное количество самых разных людей и их коллективное мнение действительно свидетельствует о компетентности президента). Сравните эту логическую ошибку с другим ложным подходом к тому же вопросу.
Оба человека, с которыми я разговаривал, считают, что президент прекрасно справляется со своими обязанностями. Я беседовал с Бертом и Эрни, а они никогда не ошибаются. Хватит уже ворчать, пора признать, что это вполне подходящий лидер для нашей страны!
В данном случае опора на, предположительно, непогрешимое мнение двух человек порождает апеллирование к мнимому авторитету. Если люди, на которых ссылаются, не являются экспертами в данной области, то такая аргументация очень слаба. Если Берт и Эрни — видные политические аналитики национального уровня, их мнение даёт основания согласиться с выводом. В противном случае перед нами аргумент, претендующий на определённость в вопросе, в котором возможно разве что слабое логическое обоснование, например:
Оба человека, с которыми я переговорил, считают, что президент прекрасно справляется со своими обязанностями. Это Берт и Эрни, а они неплохо информированы. Можно допустить, что они в чём-то правы; следовательно, у вас есть основания хотя бы частично пересмотреть своё отношение.
Это уже не ложный аргумент, поскольку он не выдаёт слабо подкреплённое логическими доводами субъективное мнение за безусловную истину. Однако именно иллюзия бесспорности придает ошибочной логике убедительность. Во многих ложных умозаключениях слабый индуктивный аргумент выдаётся за весомый дедуктивный, что, в свою очередь, позволяет упростить картину мира, к собственному успокоению.
Любое ложное умозаключение опирается на выявляемую безосновательную скрытую предпосылку. Это либо обобщение, претендующее на роль убедительного подтверждения вывода (в лучшем случае едва подкреплённого), либо следствие неверного понимания дедуктивной логики. Рассмотрите два типичных ложных аргумента и попробуйте обнаружить в каждом из них безосновательную скрытую предпосылку.
- Лидер оппозиции утверждает, что нравственность в нашей стране падает, как вдруг эту моралистку ловят на интрижке с мужчиной на 20 лет моложе её. Так что всем её заявлениям грош цена!
- В ходе эксперимента мы наблюдали, что повышение температуры в первом помещении привело к снижению результативности участников группы № 1. На этом основании мы утверждаем, что снижение в ходе эксперимента результативности участников группы № 2 должно было быть вызвано увеличением температуры во втором помещении.
В первом примере вводится предпосылка: «Если некто совершает поступок, идущий вразрез с его утверждениями, значит, эти утверждения ошибочны». Очевидно, что это не так. Лицемерие — повод задуматься о личности человека, но наличие этой черты не делает спорным всё, что он говорит.
Предпосылка из второго примера: «Поскольку повышение температуры в одном случае ухудшило результаты, то оно является единственно возможным объяснением ухудшения результатов во всех остальных случаях». Это неверно, поскольку результативность может снизиться по множеству других причин: ложная предпосылка свидетельствует о неверном понимании логики.
Бывает трудно указать на конкретную ошибку в цепочке рассуждений или убедить других, что существует проблема с логикой. Эффективно прояснить ситуацию позволяет метод сопоставимых примеров — построение параллельных аргументов с использованием точно такой же логики, но в рассуждениях на совершенно иную тему.
Давайте вернёмся к первому примеру этой главы, апеллирующему к популярному мнению.
Все, с кем я разговаривал, считают, что президент прекрасно справляется со своими обязанностями. Хватит уже ворчать, пора признать, что это вполне подходящий лидер для нашей страны!
Можно проверить правомочность данного рассуждения на сопоставимом примере — даже не на одном, а на трёх.
- На дворе 1066 год, и все, с кем я разговаривал, считают, что Земля плоская. Хватит уже ворчать, пора признать, что это правда!
- Никто из тех, с кем я разговаривал, не знает, что такое «искусство Терпсихоры». Хватит уже умничать, пора признать, что это бессмысленное словосочетание!
- Все находящиеся в этой комнате утверждают, что два плюс два равняется пяти. Хватит уже спорить, так оно и есть!
Как вы, безусловно, знаете, два плюс два равняется четырём, Земля не плоская, а искусство Терпсихоры — это танец. В данном случае примеры, имеющие точно такую же форму, что и анализируемый аргумент, выявляют необоснованность его фундаментальной предпосылки, помогая увидеть несостоятельность кажущегося убедительным рассуждения.
Чтобы ближе познакомиться с другими инструментами мышления и научиться отличать ложные рассуждения, читайте книгу «Критическое мышление».
Купить книгу