Одним
из первых таких строго формализованных
методов является метод Квайна. Сущность
этого метода состоит в следующем: если
над исходной СДНФ произвести сначала
все возможные операции неполного
склеивания, а затем над полученным
выражением все возможные операции
поглощения, то в результате выполненных
преобразований будет получена сокращенная
ДНФ.
Проиллюстрируем
применение метода Квайна для минимизации
логической функции
,
заданной следующей таблицей истинности
(табл. 3.1.):
Таблица
3.1
|
a |
b |
c |
|
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Выпишем
СДНФ функции
:
(3.1)
Пронумеруем
каждую конъюнкцию из (3.1) следующим
образом:
(3.2)
Затем,
склеиваем (если это возможно) каждый из
членов выражения (3.2) с последующими
членами и записываем полученные
импликанты так, как показано в таблице
3.2:
Таблица
3.2
|
Номера конъюнкций |
Импликанты, в (если |
|
1-2 |
|
|
1-3 |
|
|
1-4 |
не |
|
1-5 |
не |
|
1-6 |
не |
|
2-3 |
не |
|
2-4 |
|
|
2-5 |
не |
|
2-6 |
не |
|
3-4 |
не |
|
3-5 |
|
|
3-6 |
не |
|
4-5 |
не |
|
4-6 |
|
|
5-6 |
|
Соединяя
полученные импликанты знаками дизъюнкции,
получаем сокращенную ДНФ логической
функции
:
(3.3)
Используя
метод Квайна для минимизации логических
функций необходимо помнить о том, что
в этом методе используется операция
неполного склеивания. Если в СДНФ,
реализующей логическую функцию,
присутствует конъюнкция, которая не
может быть склеена ни с одной последующей
конъюнкцией, то эта конъюнкция должна
быть включена в полученную в результате
минимизации сокращенную ДНФ.
3.2. Метод испытания импликант
После
получения сокращенной ДНФ, к ней может
быть многократно применен метод Квайна,
в результате чего будет получена
некоторая тупиковая форма тождественная
исходной ДНФ. Более часто применяют
другой метод: метод испытания импликант
в сокращенной ДНФ логической функции.
Существо
метода состоит в следующем: из формулы,
являющейся сокращенной ДНФ, выбирается
испытуемая импликанта (можно произвольным
образом). Выбранная импликанта
приравнивается к 1. Далее определяются
значения логических переменных,
обращающих в 1 испытуемую импликанту.
Из сокращенной ДНФ удаляется испытуемая
импликанта, а в оставшуюся часть
сокращенной ДНФ подставляются найденные
значения логических переменных,
обращающих в 1 испытуемую импликанту.
Если в результате такой подстановки
значение логической функции равно
единичному значению, то испытуемая
импликанта является лишней (избыточной)
и может быть удалена из сокращенной ДНФ
логической функции. После удаления
лишней импликанты также испытываются
все импликанты, входящие в сокращенную
ДНФ.
Рассмотрим метод
испытания импликант на примере.
Пусть
логическая функция
,
представлена в виде сокращенной ДНФ,
полученной по методу Квайна (3.3):
(3.3)
Испытаем
импликанты в (3.3). Первой будем испытывать
импликанту
.
Импликанта
обращается в 1 при следующих значениях
логических переменных:
-
=1,
при
=0,
=0.
Подставляя найденные значения в (3.3),
предварительно исключив из формулы
испытуемую импликанту, получим:
импликанта
является лишней и должна быть удалена
из формулы.
Таким
же образом испытаем оставшиеся в формуле
импликанты.
-
=1,
при
=0,
=0.
импликанта
не является лишней. Оставляем ее в
формуле.
-
при
=0,
=1.
импликанта
не является лишней. Оставляем ее в
формуле.
-
=1,
при
=1,
=0.
импликанта
является лишней и должна быть удалена
из формулы.
-
=1,
при
=1,
=1.
импликанта
является лишней и должна быть удалена
из формулы.
-
=1,
при
=1,
=1.
импликанта
не является лишней. Оставляем ее в
формуле.
После
испытания импликант получаем одну из
тупиковых ДНФ логической функции
:
(3.4)
Если
начать испытание импликант в (3.3) не с
первой импликанты, а с какой-либо другой,
выбранной произвольным образом, то
можно получить некоторое количество
тождественных сокращенных и тупиковых
ДНФ, реализующих функцию.
В частности, если начать испытание
импликант с последней импликанты в
(3.3), то полученная тупиковая ДНФ для
логической функциибудет иметь вид:
(3.5)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть n = 3. Из преобразования (развертывания)
1 = 1.1.1 = (x2+ 2)(x1+
1)(x0+
0) =
2
1
0 +
2
1x0 +
2x1
0 +
2x1x0 + x2
1
0 + x2
1x0 + x2x1
0 + x2x1x0
следует смысл термина «конституента (составляющая) единицы».
Пример: пусть y = x2 1+x1x0+x2x0. Видно, что все элементарные произведения имеют ранг r = 2, следовательно правило поглощения нельзя применить; кроме того ни одна пара произведений не является соседней, так как произведения имеют различные переменные. Если же развернуть произведение x2x0 до конституент единицы (в данном случае n = 3), то выражение упростится:
y = x2 1+x1x0+x2.1.x0 = x2
1+x1x0+x2(x1+
1)x0 = x2
1+x1x0+x2x1x0+x2
1x0 = x2
1(1+x0)+x1x0(1+x2) = x2
1.1+x1x0.1 = x2
1+x1x0,
т.е. произведение x2x0 оказалось лишним.
Правило развертывания элементарной суммы ранга r до произведения элементарных сумм ранга n (конституент нуля) следует их законов нулевого множества и распределительного закона второго рода и производится в три этапа:
— в развертываемую сумму ранга r в качестве слагаемых вводится n-r нулей;
— каждый нуль представляется в виде логического произведения некоторой, не имеющейся в исходной сумме переменной и ее отрицания: xi. i = 0;
— получившееся выражение преобразуется на основе распределительного закона второго рода (14) таким образом, чтобы исходная сумма ранга r развернулась в логическое произведение 2n-r конституент нуля.
Пример: развернуть элементарную сумму x3+x2 в логическое произведение конституент нуля, зависящих от 4-х переменных. Последнее следует из того, что максимальный индекс равен 3; отсутствуют переменные x1 и x0.
Решение: x3 + 2 = x3 +
2 + 0 + 0 = x3 +
2 + x1
1 + x0
0 =
(x3+ 2+x1).(x3+
2+x1) + x0
0 = (x3 +
2 + x1 + x0).(x3 +
2 + x1 +
0).
(x3 + 2 +
1 + x0).(x3 +
2 +
1 +
0).
Пусть n = 2. Из преобразования (развертывания)
0 = 0+0 = x1 1+x0
0 = (x1
1+x0)(x1
1+
0) =
(x1+x0)( 1+x0)(x1+
0)(
1+
0)
следует смысл термина «конституента (составляющая) нуля».
Пример: пусть y = (x2+ 1) (x1+x0) (x2+x0). Ясно, что операции склеивания и поглощения здесь применить нельзя. Однако, если развернуть сумму x2+x0 до конституент нуля (в данном случае n = 3), то выражение упростится: y = (x2+
1) (x1+x0) (x2+0+x0) = (x2+
1) (x1+x0) (x2+x1
1+x0) = (x2+
1+0) (x1+x0+0) (x2+x1+x0) (x2+
1+x0) = (x2+
1+0.x0) (x1+x0+0.x2) = (x2+
1) (x1+x0), т.е. сумма x2+x0 оказалась лишней.
Этапы минимизации ФАЛ
В общем случае минимизация ФАЛ, заданной в СДНФ, требует выполнения процедур следующих трех этапов:
1 этап — переход от СДНФ к сокращенной ДНФ (СокрДНФ). СокрДНФ — это форма ФАЛ, членами которой являются изолированные (несклеивающиеся) элементарные произведения. Этот этап основан на выполнении всех возможных склеиваний друг с другом сначала конституент единицы, а затем произведений меньшего ранга (импликант). Отметим, что существуют ФАЛ, у которых СДНФ совпадает с СокрДНФ.
2 этап — переход от СокрДНФ к тупиковой ДНФ (ТДНФ). ТДНФ — это форма ФАЛ, членами которой являются импликанты, среди которых нет ни одной лишней. Лишней импликантой называется член ФАЛ, удаление которого из выражения не изменяет ФАЛ. Отметим, что возможны случаи, когда в СокрДНФ нет лишних импликант. Иногда из одной СокрДНФ можно получить несколько различных ТДНФ. Термин “тупиковая” говорит о том, что дальнейшая минимизация в рамках нормальных форм уже невозможна.
3 этап — переход от ТДНФ к минимальной форме. Этот этап основывается на использовании групповых инверсий и скобочных форм, не является систематическим и во многом определяется опытом разработчика.
Расчетный метод
Пусть нам требуется минимизировать ФАЛ, заданную выражением (9).
1 этап. для выполнения первого этапа минимизации нужно провести операции склеивания конституент единицы выражения (9).
Для упорядочения этой процедуры запишем выражение (9) в виде нескольких строк по следующему правилу: первая строка — это исходное уравнение, вторая строка — это вторая конституента и все последующие, третья строка — это третья конституента и все последующие и т.д. Это допустимо, так как в булевой алгебре действует закон тавтологии.

Производится проверка на склеивание первого члена в каждой строке со всеми остальными в данной строке. В первой строке склеиваются первая и третья конституенты, во второй строке — первая со второй и четвертой, в третьей строке первая конституента с остальными не склеивается, и в последней строке конституенты склеиваются. Поскольку все конституенты участвовали хотя бы в одном склеивании, то в СокрДНФ ни одной конституенты не будет. После этой процедуры получаем следующее выражение:
(16)
Дальнейшее склеивание не может быть выполнено, так как все члены выражения (8) являются изолированными.
2 этап.
Необходимо выявить лишние импликанты в выражении (16). Это можно сделать двумя способами.
При первом способе развертывают одну импликанту до конституент единицы, а затем смотрят, не поглощаются ли эти конституенты остальными импликантами. Первая импликанта развертывается до суммы
,
причем конституента не поглощается ни одной импликантой, следовательно, импликанта
не является лишней. Вторая импликанта
развертывается до суммы
, причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта
лишняя. Продолжим эту процедуру, оставив пока импликанту
в выражении (16). Импликанта
развертывается до суммы
, причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта
лишняя. Продолжим, оставив в выражении (16) и эту импликанту. Развертывание последней импликанты дает сумму
, в которой конституента
не поглощается ни одной импликантой, следовательно, импликанта
не является лишней. Выявлены две лишнии импликанты, но это не значит, что обе они могут быть отброшены, так как каждая из них проверялась при вхождении второй в выражение (16). Следовательно, отбросить наверняка можно одну из них, а затем снова произвести проверку возможности отбросить и другую. Если отбросить импликанту
, то проверка показывает, что импликанта
не будет лишней, а если отбросить
, то
не будет лишней. Итак, можно отбросить одну из выявленных двух импликант и в результате получаются две ТДНФ одинаковой сложности, содержащих по шесть букв:
(17)
(18)
Второй способ выявления лишних импликант заключается в следующем. На значение истинности функции влияет только та импликанта, которая сама равна 1. Любая импликанта принимает значение 1 только на одном наборе своих аргументов. Но если именно на этом наборе сумма остальных импликант также обращается в 1, то рассматриваемая импликанта не влияет на значение истинности функции даже в этом единственном случае, то есть является лишней.
Применим это правило к выражению (16).
Импликанта принимает значение 1 на наборе
,
. Подставив этот набор в оставшуюся сумму
, получим
, что говорит о том, что первая импликанта не является лишней. Импликанта
принимает значение 1 на наборе
,
. Подставив этот набор в сумму
, получим
, что говорит о том, что импликанта
лишняя.
Оставим пока эту импликанту и продолжим анализ других импликант.
Импликанта принимает значение 1 на наборе
,
. Подставив этот набор в сумму
, получим
, что говорит о том, что импликанта
лишняя.
Оставляем и ее и продолжаем процедуру.
Импликанта принимает значение 1 на наборе
,
. Подставив этот набор в сумму
, получаем
, что говорит о том, что импликанта
не является лишней.
Как и в первом случае нельзя отбрасывать обе обнаруженные лишние импликанты, так как каждая из них проверялась при вхождении другой в оставшуюся сумму. Опустим рассмотрение дальнейших процедур, так как они аналогичны процедурам, выполненным первым способом.
3 этап. Выражение (17) можно записать в виде
(19)
Оно содержит пять букв и требует три инвертора. Применив закон двойного отрицания и правило де-Моргана, выражение (19) можно преобразовать:
(20)
Последнее выражение содержит пять букв и требует два инвертора.
Аналогично можно упростить и выражение (10):
(21)
Можно сделать вывод, что даже для этого простого примера пришлось выполнять достаточно много однообразных действий, требующих внимания и времени, поэтому расчетный метод минимизации ФАЛ применяется в основном для ФАЛ, зависящих от двух или трех переменных.
Табличный метод
При этом методе два первых этапа выполняются при помощи специальных карт, впервые предложенных Вейчем и модернизированных карт Карно. Практическое применение получили именно карты Карно, а не диаграммы Вейча, и хотя с момента опубликования их оригинальных работ прошло 45 лет, до сих пор многие авторы называют карты Карно диаграммами Вейча.
Матрица Вейча отличается от матрицы Карно расположением столбцов и строк. Карно пользуется циклическим порядком следования символов как в коде Грея, а именно 00, 01, 11, 10, Вейч располагает символы в порядке возрастания двоичных чисел, а именно 00, 01, 10, 11. Столбцы или строки 00 и 01, так же как столбцы или строки 10 и 11, являются в матрице Вейча соседними, но столбцы или строки 01 и 10 в ней не являются ни соседними, ни крайними, что затрудняет их обработку. Матрица Карно оказалась более удобна в обращении. Итак, табличный метод минимизации ФАЛ это метод, основанный на использовании карт Карно.
Карта Карно является специальной формой таблицы истинности ФАЛ, позволяющей не только задать ФАЛ, но и выполнить первый и второй этапы минимизации. Таблица истинности (см. табл. 5) содержит 2n строк, в которых наборы n переменных расположены в линейной лексикографической последовательности, а также столбец значений ФАЛ на этих наборах. Напомним, что в таблице истинности переменные с большим весом располагаются слева.
Карта Карно содержит 2n клеток (квадратов), расположенных в виде строки (n = 1, 2), либо в виде двумерной матрицы (n ≥ 2). Каждая клетка, как и строка в таблице истинности, соответствует одному набору. Для того, чтобы можно было производить минимизацию ФАЛ, необходимо в смежных в геометрическом смысле клетках карты расположить соседние наборы. Это можно обеспечить, если наборы переменных, определяющих “координаты” клетки карты Карно, расположить в циклическом коде Грея, у которого каждое следующее значение отличается от предыдущего только в одном разряде.
На рис. 8 представлена так называемая эталонная карта Карно для n = 3. Она служит для указания расположения переменных, как координат клеток, так и наборов этих переменных. Координатой клеток в горизонтальном направлении служат наборы переменных , а координатой клеток в вертикальном направлении служит одна переменная
.
Аннотация: В данной лекции представлены способы минимизации на основе метода проб, метода Квайна-Мак-Класки, на основе минимизирующих диаграмм для функции 2-х, 3-х, 4-х переменных (диаграммы Вейча).
Рассмотрим произвольную ДНФ. Если в ней выбросить любое произведение, то оставшееся выражение будет принимать нулевое значение на тех наборах, что и исходная форма, т.к. 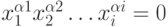
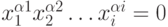
Однако, если отброшенное произведение (импликанта) обращалось в единицу, и функция принимала единичное значение на этом единственном наборе, то оставшееся выражение может уже не принять единичное значение на данном наборе. Это означает, что импликанта не была лишней. Если же с помощью проверки установить, что оставшееся выражение обращается в единицу, импликанта – лишняя, и ее можно отбросить.
Пример 1:
Пусть дана
-
Отбросим член x1x2:
x1x2 = 1 => x1 = 0, x2 = 0
Т.к.
то x1x2 исключить нельзя
-
Отбросим член x1x3:
x1x3 = 1 => x1 = 1, x3 = 1
1 => x1x3 исключить нельзя.
- Отбросим член x2x3:
x2x3 = 1 => x2 = 0, x3 = 1
=> x2x3 — член лишний.
Если проверка показывает, что несколько импликант одновременно являются лишними, то исключить их одновременно из выражения ДНФ нельзя. Это можно выполнять лишь поочередно.
Пример 2:
- испытаем 1 член: x1x3x4 = 1; x1 = 0; x3 = 1; x4 = 1
Т.е. член x1x3x4 исключить нельзя.
- испытаем 2 член: x2x3x4 = 1; x2 = 0; x3 = x4 = 1
Т.е. член x2x3x4 лишний.
- испытаем 3 член: x1x2x4 ; x1 = 1; x2 = 0 x4 = 1
Т.е. член x1x2x4 лишний.
- испытаем 4 член: x1x2x3 ; x1 = 1; x2 = x3 = 0
, Т.е. член x1x2x3 лишний.
- испытаем 5 член: x2x3x4 ; x2 = x3 = x4 = 0
, Т.е. член x2x3x4 не лишний.
Исключим одновременно члены 2, 3, 4
Проверим значения f одновременно на тех наборах, на которых обращаются в единицу все отброшенные члены.
т.е. видно, что во всей совокупности этого сделать нельзя
Исключим член x2x3x4, получим:
Проверим, не являются ли в этом выражении лишними те члены, которые оказались лишними в исходном выражении, т.е.: x1x2x4 и x1x2x3.
- проверим x1x2x4:
x1 = 1; x2 = 0; x4 = 1
т.е. член x1x2x4 не лишний
- проверим x1x2x3:
x1 = 1; x2 = x3 = 0
, т.е. член x1x2x3 лишний,
Поэтому 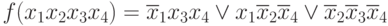
Проверяя затем, начав с исключения третьего члена, получим другую тупиковую форму. Затем выберем из них минимальную.
Недостаток метода заключается в том, что при большом числе членов он становится громоздким, поскольку связан с перебором различных вариантов. Машинная реализация данного метода вследствие этого сложна. При автоматизации поиска минимальных форм метод практически не используется.

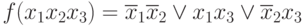

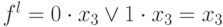
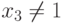 то
то 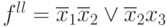
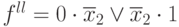
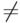 1 =>
1 => 
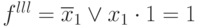 =>
=> 
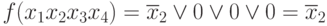 Т.е. член
Т.е. член 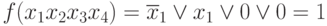 Т.е. член
Т.е. член 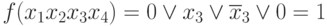 Т.е. член
Т.е. член 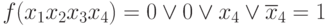 , Т.е. член
, Т.е. член 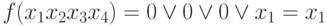 , Т.е. член
, Т.е. член 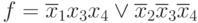

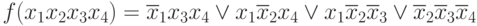
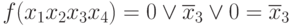 т.е. член
т.е. член 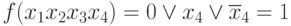 , т.е. член
, т.е. член