Как найти линейные размеры тела

Лабораторная работа

«ИЗМЕРЕНИЕ ЛИНЕЙНЫХ РАЗМЕРОВ ТЕЛ»

Цель работы: измерить линейные размеры бруска и диаметр проволоки.

Оборудование: линейка, штангенциркуль, 2 бруска разных размеров, два куска проволоки разного диаметра.

ТЕОРИЯ

1. Оценка погрешностей измерений

Измерение физической величины заключается в сравнении измеряемой величины с эталоном.

Измерить физическую величину – это значит с использованием специальных технических средств (средств измерения) опытным путём найти значение физической величины, а также степень её приближения к истинному значению, которое в принципе неизвестно.

В данной работе линейные размеры измеряемого тела сравниваются с расстоянием между штрихами на рабочей поверхности измерительного инструмента. Точность измерений определяется точностью нанесения штрихов на рабочей поверхности инструмента и точностью определения положения измеряемого тела относительно измерительного инструмента, например, линейки длиной 30 – 50 см изготавливаются с точностью до 1 мм.

Максимальную погрешность измерения, обусловленную неточностью изготовления инструмента, называют допустимой инструментальной погрешностью или границей абсолютной инструментальной погрешности. Её обозначают ∆ и . Она равна цене деления прибора.

При выполнении измерений возникает погрешность отсчета – погрешность, обусловленная необходимостью округления результата с избытком или недостатком при установлении стрелки на шкале. Её обозначают ∆ 0. Максимальное значение её можно принять равной:

— половине цены деления, если стрелка прибора неподвижна.

— цене деления, если стрелка колеблется (измерения в движущейся системе).

Граница абсолютной погрешности измерения (её обозначают ∆) складывается из границы инструментальной погрешности и границы погрешности отсчета:

| ∆ | = | ∆ и | + | ∆ 0 |      (1)

Вторым показателем качества измерений является максимальная относительная погрешность. Отношение максимальной абсолютной погрешности к модулю приближенного значения измеряемой величины называют максимальной относительной погрешностью или границей относительной погрешности. Её обозначают ξ и выражают числом без наименования или в процентах:

                | ∆ |              | ∆ |

                            ξ = ——- или   ξ = ——- · 100 %   (2)

                                                            а                     а

2. Измерительные приборы

2.1. Линейка.

Линейка в общем виде представляет собой протяженный объект с ровным краем.

На линейку вдоль края нанесена шкала с длинными и короткими штрихами. Отметка «0» соответствует началу отсчета. На школьной линейке длинные штрихи соответствуют сантиметрам, короткие – миллиметрам. Отрезок между двумя длинными штрихами разделен короткими штрихами на 10 равных частей: 1 см = 10 мм.

                                           1 см – 0 см                    см         мм

Цена деления линейки ЦД = ——————— = 0,1 ——- = 1 ——-

                                            10 делений                  дел.       дел.

Характеристики линейки:

— цена деления………………………………………………………………………..1мм

— инструментальная погрешность…………± цена деления…………±1 мм

— погрешность отсчета……………………….пол цены деления….….0,5 мм

— абсолютная погрешность измерения……(формула (1))…….…1,5 мм

При измерении линейных размеров тел поступают так:

— тело помещают на опору, например, на стол;

— линейку прикладывают к измеряемой грани так, что нуль на шкале линейки совпадает с одним краем грани тела;

— смотрят, с каким делением на шкале линейки совпадает другой край грани тела;

— по количеству штрихов N между нулем и этим делением с использованием цены деления шкалы (ЦД) определяют линейный размер (длину тела или его части).

L = (ЦД) · N    (3)

2.2. Штангенциркуль

Штангенциркуль представляет собой протяженный объект, состоящий из двух подвижным образом соединенных частей. Каждая часть снабжена шкалой разной цены деления. Одна часть называется основой (базой) и имеет шкалу обычной линейки, а, значит, и её характеристики. Другая часть называется подвижной линейкой (нониусом) и её шкала позволяет измерять десятые доли миллиметра. Точность измерения линейных размеров тел с помощью штангенциркуля выше, чем при измерении линейкой. Шкала нониуса имеет 10 делений на подвижной линейке; цена деления составляет 0,9 мм. Название – нониус – произошло от фамилии автора – португальского математика Нуниша (пишется Nonius).

Штангенциркуль снабжен двумя парами губок. Между первыми зажимается измеряемый объект, а вторые вставляются в отверстие.

При пользовании штангенциркулем показания снимают по двум шкалам: по базовой шкале длину в миллиметрах, а по штриху подвижной шкалы, совпавшему с миллиметровым штрихом неподвижной шкалы, отсчитывают десятые доли миллиметра.

Характеристики штангенциркуля:

— цена деления базы (ЦД 1)…………………………………………………….………………………1 мм

— цена деления нониуса (ЦД 2)………………………………………………………..………………0,1 мм

— инструментальная погрешность…… …. ± минимальная цена деления…………. ± 0,1 мм

— погрешность отсчета…………………….минимальная цена деления…………………..….0,1 мм

— абсолютная погрешность измерения……(формула (1))…………………………….………0,2 мм

2.3. Пример использования штангенциркуля

При измерении предмет зажимают между неподвижной и подвижной частями штангенциркуля. Если нуль шкалы нониуса при этом точно попал на миллиметровое деление основной шкалы, размер предмета равен целому числу миллиметров (показанию основной шкалы).

Если размер предмета не равен целому числу миллиметров, то нуль шкалы нониуса попадет между двумя делениями основной шкалы. В этом случае и работает шкала нониуса, которая позволяет определить размер предмета с точностью до 0,1 мм.

Это делается так. Поскольку цена деления шкалы нониуса равна 0,9 мм, то 10 делений шкалы нониуса (полная шкала) равны 9 мм, 9 делений шкалы нониуса – 8,1 мм, 8 делений шкалы – 7,2 мм, 7 делений – 6,3 мм, 6 делений – 5,4 мм, 5 делений – 4,5 мм, 4 деления – 3,6 мм, 3 деления – 2,7 мм, 2 деления – 1,8 мм, 1 деление – 0,9 мм.

Если размер предмета равен целому числу миллиметров плюс 0,9 мм, расстояние от нуля шкалы нониуса до следующего миллиметрового деления основной шкалы будет равно 0,1 мм, и с одним из делений основной шкалы совпадет девятое деление шкалы нониуса (поскольку оно находится от нуля шкалы нониуса на расстоянии 8,1 мм).

Если размер предмета равен целому числу миллиметров плюс 0,8 мм, расстояние между нулем шкалы нониуса и следующим миллиметровым делением основной шкалы равно 0,2 мм, и с одним из делений основной шкалы совпадет восьмое деление шкалы нониуса. Если размер предмета равен целому числу миллиметров плюс 0,7 мм, расстояние между нулем шкалы нониуса и следующим миллиметровым делением основной шкалы равно 0,3 мм, и с одним из целых значений основной шкалы совпадет седьмое деление шкалы нониуса. И т.д.

  Таким образом, размер предмета определяется так: он равен целому числу миллиметровых делений основной шкалы, которое «перешагнул» нуль шкалы нониуса, и такому числу десятых долей миллиметра, какое деление шкалы нониуса точно совпало с одним из миллиметровых делений основной шкалы (для примера, показанного на рисунке, — 7,6 мм).

ВЫПОЛНЕНИЕ

1. Используя инструкцию (см. пункт № 2.1 «Линейка»), определите длину, ширину, высоту бруска 1, бруска 2.

2. Заполните таблицу № 1 «Линейные размеры бруска».

Таблица № 1.

3. Сравните абсолютные и относительные погрешности, сделайте вывод.

4. Используя инструкцию (см. пункт № 2.2 «Штангенциркуль»), определите диаметр проволоки.

5. Заполните таблицу № 2 «Диаметр проволоки».

Таблица № 2.

6. Проанализируйте таблицы, сделайте выводы о точности произведённых измерений.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение:

— цены деления прибора.

— инструментальной погрешности.

— абсолютной погрешности отсчета.

— абсолютной погрешности измерения.

— относительной погрешности.

2. Что означает фраза «измерить физическую величину»?

3. Как нужно производить измерения линейных размеров тел с помощью:

— линейки?

— штангенциркуля?

4. Какова точность измерения при совмещении края грани тела не с нулём, а с любым делением шкалы?

5. Как использовать линейку для измерения диаметра проволоки? Разработайте методику проведения опыта и методику вычисления погрешностей.

Примечание.

1.Можно построить график зависимости относительного удлинения от длины.

2. Результат измерения можно представить в виде двойного неравенства, показать диаграмму.

Министерство
образования Российской Федерации

Томский политехнический
университет

Кафедра ТиЭФ

ОТЧЕТ ПО
ЛАБОРАТОРНОЙ РАБОТЕ М-00

Определение
линейных величин

Исполнитель:

студент группы
Э7А40 А. В. Кобеев

(подпись)

Руководитель
М.И. Чебодаев

(подпись)

(дата)

Томск – 2004

Цель
работы:
измерить размеры тел с помощью
штангенциркуля и микрометра; ознакомиться
с методом подсчета погрешности.

Краткое
теоретическое содержание работы

Масштабными
линейками
производят измерение длины. Величина
наименьшего деления такой линейки
называется ценой одного деления. Обычно
цена одного деления равна 1 мм.

Штангенциркуль
состоит из
линейки со шкалой имеющей миллиметровые
деления, и нониуса – дополнительной
линейки, которая может перемещаться
вдоль шкалы.

Линейным
нониусом называется
маленькая линейка с делениями, которая
может скользить вдоль большой линейки
так же с делениями, называется масштабом.

Микрометр
состоит из двух основных частей: скобы
и втулки, имеющей с внутренней стороны
микрометрическую резьбу, а на поверхности
– шкалу с делениями в 0.5 мм и продольную
черту

Угловой
нониус
представляет собой дуговую линейку,
укрепленную на штанге, разделенную на
градусы и на части градуса; нониус можно
перемещать по окружности или полуокружности
лимба. Цена деления шкалы нониуса не
равна цене деления шкалы лимба.

Точность
кругового нониуса определяется по
формуле:

,где
m
–число делений нониуса;
—
цена деления шкалы
нониуса;
-цена
деления лимба

Точность
нониуса определяется по формуле:
,где
M
– число делений нониуса; Y
– расстояние между соседними штрихами
масштаба; Х – расстояние между соседними
штрихами нониуса.

Различают два вида
измерений:

1. Прямые –измерения,
   полученные с помощью различных
   измерительных приборов.

2. Косвенные
   –измерения, полученные с помощью
   формул.

Различают три вида
ошибок:

1. систематические
   –ошибки, сохраняющие величину и знак
   от опыта к опыту, проводящиеся в
   одинаковых условиях

2. приборные
   –ошибки, зависящие от точности измерения
   величины каким-либо прибором.

3. случайные –ошибки,
   изменяющие свою величину или знак от
   опыта к опыту.

Расчетные формулы:

,
где a,
b,
c
– стороны параллепипеда

,где
d
– диаметр цилиндра, h
– его высота

,где
—
среднеквадратичная ошибка
среднеарифметического величины
;
N
– количество измерений

,где

-случайная
погрешность ;
–
коэффициент Стьюдента

, где

— ошибка однократного
измерения величины

;
–
точность нониуса ;
=0,95-
доверительный коэффициент

,где
—
общая ошибка величины

,где
—
погрешность косвенных измерений

,
где
—
общая погрешность величины

Схема установки

Для измерения
линейных величин в данной работе
используются приборы: штангенциркуль
и микрометр

Основными частями
которых являются шкала, называемая
масштабом ( цена деления 1 мм) и нониус
( цена деления 0,9 мм)

Точность нониуса
для штангенциркуля равна:
,где
y=1
мм, m=10

Для L
отрезка, измеряемая пробором, имеющим
нониус, равна

,где k-
целое число деления масштаба, измеряемого
тела ; n
– ближайшие к делению масштаба деление
нониуса

Нониус микроскопического
винта(конический нониус) представляет
собой барабан с 50 делениями, точность
нониуса микрометра

Результаты
измерений линейных размеров тел

11144,88

7018,23

Обработка
результатов измерений

1.Погрешность
прямых измерений

Вычисление
среднеквадратичной погрешности для
длины, ширины и высоты тела по формуле

0,05
мм

мм

мм

0,14
мм

Погрешность
однократных измерений штангенциркуля

= 0,02375 мм ,где
=
0,05 мм так как a,
b, c измерено штангенциркулем с точностью
0,05 мм

Общая ошибка
прямых измерений a,
b, c

0,142
мм

0,142
мм

2. Вычисление
средней квадратичной погрешности
диаметра и высоты

мм

0,13
мм

мм

мм

Погрешность
однократных измерений

=
=
=
0,00475 мм ,где
=
=0,01
мм так как a,
b, c измерено микрометром с точностью
0,01 мм

мм

мм

3. Погрешность
косвенных измерений

=
0,033

Абсолютная
погрешность

=
231

Окончательный
результат

с доверительной
вероятностью
=0,95

с доверительной
вероятностью
=0,95

Вывод

После проведения
данной лабораторной работы можно сказать
то, что точное и правильное измерение
физической величины во время наблюдений
и опытов составляет главную часть
всякого научного исследования в физике.
Все физические измерения могут быть
произведены с ограниченной точностью.
Ограниченная точности ставят предел
степени полученной информации, полученной
из опыта, только в пределах точности
измерений можно сравнить результаты
различных опытов.

Соседние файлы в папке M — 00

• #

  30.05.201559.08 Кб1463.tif

• #

  30.05.2015396.54 Кб1134.jpg

• #

  30.05.201589.25 Кб1504.tif

• #

  30.05.201544.03 Кб2135.tif

• #
• #

Введение

Линейный размер твёрдого тела – это, как правило, его длина, ширина и высота.

Длина – это расстояние между концами отрезка прямой, измеренное каким-либо отрезком, принятым за единицу длины.

В системе СИ единицей длины является метр (м). Метр (франц. metre, от греч.  — мера – это длина пути, который проходит луч света в вакууме за 1/299792458 долю секунды. Миллиметр (от лат. mille – тысяча и —метр) – тысячная доля метра.

Площадь – одна из количественных характеристик плоских геометрических фигур и поверхностей. Площадь прямоугольника равна произведению длин двух его сторон. Единица её измерения в СИ – м².

Объём – одна из количественных характеристик геометрических тел. Объём прямоугольного параллелепи-педа равен произведению длин трёх его смежных сторон. Единица измерения объёма – м³.

Линейные размеры определяют методом (от греч.  — исследование) прямого измерения. Прямые измерения – это такие измерения, в результате которых измеряемый размер определяется прямым сравнением измеряемой величины с единицей измерения посредст-вом меры или измерительного прибора, програ-дуированного в принятых единицах измерения.

Площадь и объём фигуры находят косвенным методом. Косвенные измерения – это такие измерения, в результате которых искомая величина определяется на основе прямых измерений. При этом измеряют величины, связанные с искомой величиной определённой функ-

циональной зависимостью, а результат получают по известным соотношениям между измеренными величина-ми и искомой.

К средствам измерений относят меры, измерительные приборы и преобразователи, а также состоящие из них измерительные установки и системы.

В настоящее время для измерения линейных размеров применяют самые разнообразные измерительные прибо-ры и инструменты.

1. Средства измерения линейных размеров

Средства измерения линейных и угловых величин:

1. Меры:

— концевые (плитки): плоскопараллельные и угловые;

— штриховые: шкалы линейные и угловые (лимбы, от лат. limbus – кайма), линейки, рулетки и угломеры;

— штангенинструмент: штангенциркули, штангенвысо-томеры (штангенрейсмасы), штангенглубиномеры, штриховые угломеры (с нониусом).

1. Микрометрические инструменты: микрометры глад-кие, нутромеры и глубиномеры.

2. Механические приборы: рычажные, с зубчатой передачей, с пружинной передачей, с рычажно-зубча-той передачей.

3. Оптико-механические приборы: оптиметры, пружин-но-оптические головки, измерительные микроскопы, длиномеры, измерительные машины, проекторы.

4. Пневматические приборы: ротаметры (поплавковые длиномеры), манометрические.

1. Приборы для измерения шероховатости поверхности: щуповые и оптические.

2. Приборы для измерения зубчатых колёс.

3. Приборы для измерения резьб.

4. Приборы для измерения подшипников.

5. Приборы для измерения отклонений формы, располо-жения, волнистости.

Механические приборы и инструменты превалируют в измерениях линейно-угловых величин. Это объясняется простотой их применения, портативностью (фр. portatif от porte — носить), отсутствием необходимости подведения извне энергии для специального освещения или питания, сравнительно высокой надёжностью и долговечностью, невысокой стоимостью.

1.1. Концевые меры длины

Мера – тело, воспроизводящее единицу измерения.

Исходная мера, воспроизводящая основную единицу измерения, называется эталоном (фр. etalon).

От государственного эталона размеры метра и его до-лей передаются на рабочие штриховые и концевые меры длины, а затем – на изделия.

Концевая мера длины имеет форму прямоугольного параллелепипеда с двумя плоскими параллельными измерительными поверхностями и изготовлена из стали по ГОСТ 9038 – 83 (рис. 1.1.1).

Концевые меры служат для хранения единицы длины и передачи размера от эталона длины до изделия. С их помощью поверяют, градуируют и устанавливают на размер измерительные приборы и инструменты, произво-дят особо точные разметочные работы.

Рис. 1.1.1. Концевая мера длины

За рабочий размер концевой меры принимают её срединную длину, т.е. длину перпендикуляра, опущен-ного из середины одной из измерительных поверхностей меры на противоположную.

Разность между наибольшей и наименьшей длинами концевой меры называется её отклонением от плоскопараллельности, она должна лежать в заданных достаточно узких границах (0,16 – 0,35 мкм).

Номинальные размеры концевых мер установлены в пределах от 0,1 до 2000 мм с градацией (лат. gradatio –постепенное повышение, от gradus — ступень, степень) 0,001, 0,01, 0,5, 10, 25, 50, 100 и 1000 мм.

Шероховатость измерительных поверхностей концевых мер должна быть настолько малой (порядка 0,06 мкм), чтобы придать мерам притираемость. Притираемость – это свойство поверхностей, обеспечи-вающее прочное сцепление концевых мер между собой, а также с плоской стеклянной или кварцевой пластинами при прикладывании или надвигании одной меры на другую или меры на пластину. Притираемость необходима при сборке концевых мер в блоки из нескольких штук. Они должны выдерживать не менее 500 притираний друг к другу.

Концевые меры комплектуют в наборы, каждому из которых присвоен определённый номер (всего 20 номеров). Номинальные размеры мер, входящих в эти наборы, составляет арифметическую прогрессию с разностью 0,001, 0,01, 0,5, 1 и 10 мм.

По точности изготовления концевых мер их наборы подразделяют на четыре класса: 0, 1, 2, 3, из которых высшим является нулевой. Кроме того, для мер, находящихся в эксплуатации, установлены дополни-тельно 4 и 5-й классы, а по соглашению сторон изготовля-ют меры класса 00.

Концевые меры применяют для непосредственных измерений размеров деталей и калибров, причём при измерении диаметров отверстий радиусные боковинки притираются к блокам плиток. По концевым мерам производят настройку приборов на нулевую отметку шкалы при относительных измерениях, градуировку (нанесение отметок) и тарировку (определение цены деления) шкал приборов; поверку приборов, а также точную настройку станков на размер. Наборы образцовых мер на заводах служат средством хранения единицы длины.

1.2. Линейка масштабная

Линейка – простейшее устройство для измерения линейных размеров, представляющее собой тонкую плас-тину с нанесённой на неё масштабной шкалой.

Металлические линейки делают из стальной пружинной термообработанной ленты толщиной 0,4 – 1 мм с ценой деления 0,5 и 1 мм. Их длина составляет 150, 300, 500 или 1000 мм. Допускаемые отклонения общей длины, в зависимости от её величины, составляют от  0,10 до  0,20 мм, сантиметровых делений  0,10 мм, а миллиметровых  0,05 мм.

Внешний вид линейки представлен на рис. 1.2.1.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Рис. 1.2.1. Линейка

Технические характеристики линейки масштабной:

— диапазон измерений, мм 0 – 300

— цена деления, мм 1

— предел допускаемой погрешности, мм 0,5

1.3. Штангенциркуль

Штангенциркуль (от нем. Stangenzirkel, Stange – стержень, прут и Zirkel, от лат. circulus – круглый, циркуль) – универсальный измерительный инструмент для определения наружных и внутренних линейных размеров абсолютным контактным методом, а также разметочных работ.

Он основан на использовании нониуса (от Nonius – от латинизированного имени португальского математика и изобретателя этой шкалы П. Нуниша (P. Nunes, 1492 — 1577)), т.е. вспомогательной шкалы, по которой отсчитывают доли делений основной шкалы какого-либо средства измерения. Нониус служит для повышения точности отсчёта по масштабной линейке и тем самым точности измерения. Конструктивно он оформлен в виде дополнительной металлической пластины с делениями, укреплённой на подвижной рамке.

Погрешность отсчёта измерения по нониусу c составляет

c = , (1.3.1)

где a – интервал деления основной шкалы (обычно 1 мм); n – число делений шкалы нониуса.

На рис. 1.3.1 изображён штангенциркуль, который состоит из штанги 1 с нанесённой на ней основной миллиметровой шкалой и перемещаемой от руки рамкой 2 со шкалой нониуса, обеспечивающей точность отсчёта по шкале штанги до 0,05 или 0,1 мм. На штанге и рамке имеются губки 3 и 4 для наружных измерений. При сомкнутых губках отсчёт по шкале равен нулю.

Штангенциркули с величиной отсчёта по нониусу 0,05 мм имеют допустимую погрешность показаний 0,05 мм для предела измерения до 500 мм.

2 1

4 3

Рис. 1.3.1. Штангенциркуль:

1 – штанга; 2 – рамка со шкалой нониуса; 3, 4 — губки

Штангенциркуль ШЦ1 модели 221111 имеет следующие технические характеристики:

Линейные
размеры средств измерения линейных размеров

Линейный размер
твёрдого тела – это, как правило, его длина, ширина и высота.

Длина – это
расстояние между концами отрезка прямой, измеренное каким-либо отрезком,
принятым за единицу длины.

 – это длина пути,
который проходит луч света в вакууме за 1/299792458 долю секунды. Миллиметр (от
лат.) — мераnortemВ
системе СИ единицей длины является метр (м). Метр (франц. metre, от греч.
 mille – тысяча и -метр) – тысячная доля метра.

Площадь – одна из
количественных характеристик плоских геометрических фигур и поверхностей.
Площадь прямоугольника равна произведению длин двух его сторон. Единица её
измерения в СИ – м2.

Объём – одна из
количественных характеристик геометрических тел. Объём прямоугольного параллелепи-педа
равен произведению длин трёх его смежных сторон. Единица измерения объёма – м3.

 — исследование)
прямого измерения. Прямые измерения – это такие измерения, в результате которых
измеряемый размер определяется прямым сравнением измеряемой величины с единицей
измерения посредст-вом меры или измерительного прибора, програ-дуированного в
принятых единицах измерения.sodohtemЛинейные
размеры определяют методом (от греч.

Площадь и объём
фигуры находят косвенным методом. Косвенные измерения – это такие измерения, в
результате которых искомая величина определяется на основе прямых измерений.
При этом измеряют величины, связанные с искомой величиной определённой функ-

циональной
зависимостью, а результат получают по известным соотношениям между измеренными
величина-ми и искомой.

К средствам измерений
относят меры, измерительные приборы и преобразователи, а также состоящие из них
измерительные установки и системы.

В настоящее время для
измерения линейных размеров применяют самые разнообразные измерительные прибо-ры
и инструменты.

1. Средства измерения
линейных размеров

Средства измерения
линейных и угловых величин:

Меры:

— концевые (плитки):
плоскопараллельные и угловые;

— штриховые: шкалы
линейные и угловые (лимбы, от лат. limbus– кайма), линейки, рулетки и угломеры;

— штангенинструмент:
штангенциркули, штангенвысо-томеры (штангенрейсмасы), штангенглубиномеры,
штриховые угломеры (с нониусом).

Микрометрические
инструменты: микрометры глад-кие, нутромеры и глубиномеры.

Механические приборы:
рычажные, с зубчатой передачей, с пружинной передачей, с рычажно-зубча-той
передачей.

Оптико-механические
приборы: оптиметры, пружин-но-оптические головки, измерительные микроскопы,
длиномеры, измерительные машины, проекторы.

Пневматические
приборы: ротаметры (поплавковые длиномеры), манометрические.

Приборы для измерения
шероховатости поверхности: щуповые и оптические.

Приборы для измерения
зубчатых колёс.

Приборы для измерения
резьб.

Приборы для измерения
подшипников.

Приборы для измерения
отклонений формы, располо-жения, волнистости.

Механические приборы
и инструменты превалируют в измерениях линейно-угловых величин. Это объясняется
простотой их применения, портативностью (фр. portatifотporte- носить),
отсутствием необходимости подведения извне энергии для специального освещения
или питания, сравнительно высокой надёжностью и долговечностью, невысокой
стоимостью.

1.1. Концевые меры
длины

1. Средства измерения
линейных размеров

Средства измерения
линейных и угловых величин:

Меры:

— концевые (плитки):
плоскопараллельные и угловые;

— штриховые: шкалы
линейные и угловые (лимбы, от лат. limbus– кайма), линейки, рулетки и
угломеры;

— штангенинструмент:
штангенциркули, штангенвысо-томеры (штангенрейсмасы), штангенглубиномеры,
штриховые угломеры (с нониусом).

Микрометрические
инструменты: микрометры глад-кие, нутромеры и глубиномеры.

Механические приборы:
рычажные, с зубчатой передачей, с пружинной передачей, с рычажно-зубча-той
передачей.

Оптико-механические
приборы: оптиметры, пружин-но-оптические головки, измерительные микроскопы,
длиномеры, измерительные машины, проекторы.

Пневматические
приборы: ротаметры (поплавковые длиномеры), манометрические.

Приборы для измерения
шероховатости поверхности: щуповые и оптические.

Приборы для измерения
зубчатых колёс.

Приборы для измерения
резьб.

Приборы для измерения
подшипников.

Приборы для измерения
отклонений формы, располо-жения, волнистости.

Механические приборы
и инструменты превалируют в измерениях линейно-угловых величин. Это объясняется
простотой их применения, портативностью (фр. portatifотporte- носить),
отсутствием необходимости подведения извне энергии для специального освещения
или питания, сравнительно высокой надёжностью и долговечностью, невысокой
стоимостью.

1.1. Концевые меры
длины

Мера – тело,
воспроизводящее единицу измерения.

Исходная мера,
воспроизводящая основную единицу измерения, называется эталоном (фр. etalon).

От государственного
эталона размеры метра и его до-лей передаются на рабочие штриховые и концевые
меры длины, а затем – на изделия.

Концевая мера длины
имеет форму прямоугольного параллелепипеда с двумя плоскими параллельными
измерительными поверхностями и изготовлена из стали по ГОСТ 9038 – 83/

Концевые меры служат
для хранения единицы длины и передачи размера от эталона длины до изделия. С их
помощью поверяют, градуируют и устанавливают на размер измерительные приборы и
инструменты, произво-дят особо точные разметочные работы.

За рабочий размер
концевой меры принимают её срединную длину, т.е. длину перпендикуляра,
опущен-ного из середины одной из измерительных поверхностей меры на
противоположную.

Разность между
наибольшей и наименьшей длинами концевой меры называется её отклонением от
плоскопараллельности, она должна лежать в заданных достаточно узких границах
(0,16 – 0,35 мкм).

Номинальные размеры
концевых мер установлены в пределах от 0,1 до 2000 мм с градацией
(лат. gradatio–постепенное повышение, отgradus- ступень, степень) 0,001,
0,01, 0,5, 10, 25, 50, 100 и 1000 мм.

Шероховатость
измерительных поверхностей концевых мер должна быть настолько малой (порядка
0,06 мкм), чтобы придать мерам притираемость. Притираемость – это свойство
поверхностей, обеспечи-вающее прочное сцепление концевых мер между собой, а
также с плоской стеклянной или кварцевой пластинами при прикладывании или надвигании
одной меры на другую или меры на пластину. Притираемость необходима при сборке
концевых мер в блоки из нескольких штук. Они должны выдерживать не менее 500
притираний друг к другу.

Концевые меры
комплектуют в наборы, каждому из которых присвоен определённый номер (всего 20
номеров). Номинальные размеры мер, входящих в эти наборы, составляет
арифметическую прогрессию с разностью 0,001, 0,01, 0,5, 1 и 10 мм.

По точности
изготовления концевых мер их наборы подразделяют на четыре класса: 0, 1, 2, 3,
из которых высшим является нулевой. Кроме того, для мер, находящихся в
эксплуатации, установлены дополни-тельно 4 и 5-й классы, а по соглашению сторон
изготовля-ют меры класса 00.

Концевые меры
применяют для непосредственных измерений размеров деталей и калибров, причём
при измерении диаметров отверстий радиусные боковинки притираются к блокам
плиток. По концевым мерам производят настройку приборов на нулевую отметку
шкалы при относительных измерениях, градуировку (нанесение отметок) и тарировку
(определение цены деления) шкал приборов; поверку приборов, а также точную
настройку станков на размер. Наборы образцовых мер на заводах служат средством
хранения единицы длины.

Гипермаркет знаний>>Физика>>Физика 7 класс>> Лабораторная работа № 4. Измерение линейных размеров тел и площади их поверхности

Тема.  Измерение  линейных  размеров  тел и площади их поверхности.

Цель:  измерить  линейные  размеры  бруска с  помощью  разных  средств  измерения,  на­учиться  определять  площадь  плоских фигур  правильной и неправильной формы.

Оборудование:  мерная  лента,  ученическая линейка,  брусок  деревянный,  лист  бумаги в клетку.

Теоретические сведения

1.  Каждое  физическое  тело  обладает  свойством  занимать  определенную часть пространства,  то есть иметь некоторую протяженность.

К  физическим величинам,  которые  являются  мерой  этого  свойства тела,  относят,  прежде  всего,  линейные  размеры  тела —  длину  (l),  высо­ту (h) и ширину (d). Поскольку длина,  высота, ширина — это физические величины,  их можно измерять,  то  есть  сравнивать  с  однородной  величи­ной,  принятой  за единицу.

За  единицу  длины  (высоты  или  ширины)  в Международной  системе единиц  (СИ)  принят метр  (м).

Площадь  поверхности  тела  также  является  физической  величиной. Единицей  площади в СИ является квадратный метр  (м²).

Напоминаем:  квадратный  метр  равен  площади  квадрата  со  стороной 1 метр.

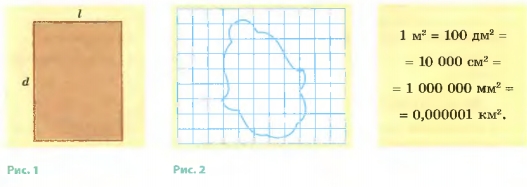
2. Площади  плоских  фигур  правильной  геометрической  формы,  например прямоугольников,  треугольников,  кругов,  обычно  определяют  с  помо­щью косвенных измерений. Сначала измеряют линейные размеры фигуры (длину,  высоту, ширину, радиус),  а потом вычисляют площадь, пользуясь соответствующими математическими формулами.  Так,  чтобы  определить площадь прямоугольника, надо умножить длину прямоугольника I на его ширину d  (рис.  1):  S =  I x d.

3. Если фигура  имеет неправильную  геометрическую форму,  то ее площадь можно  определить,  начертив  контур  этой  фигуры  на  бумаге  в  клеточку или  с помощью  палетки  . В  этом  случае площадь фигуры  вычисляют по формуле

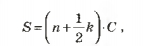
где  n —  количество  целых  квадратиков;  k —  количество нецелых  квад­ратиков,  С —  площадь  одного  квадратика.  Например,  площадь  фигуры на рис.  2  равна

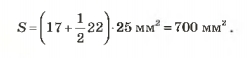
Указания к работе

Подготовка к эксперименту

1. Прежде чем  приступить к измерениям,  вспомните:

а) как  определить цену деления шкалы;
б) как правильно снимать показания прибора.

2. Определите и  запишите цену деления шкал мерной ленты и линейки.

3. Вычислите площадь, которую занимает одна клеточка на странице вашей тетради.

Эксперимент

1. С  помощью  мерной  ленты  определите  длину  I,  ширину  d  и  высоту  h бруска.

2. Повторите все измерения,  используя линейку.

3. Пользуясь полученными данными, вычислите площадь поверхности боль­шей грани  бруска.

4  Результаты всех измерений  занесите в табл. 1.

Таблица 1

6. Подсчитайте  количество  целых  n  и  нецелых  k  квадратиков  внутри  кон­тура.

7.  Вычислите площадь грани бруска.

8.  Результаты вычислений занесите в  табл.  2.

Таблица 2

Анализ результатов эксперимента

1.  Сравните результаты измерений линейных размеров бруска (табл.  I) и вы­ясните,  каким  из  имеющихся  у  вас  приборов  целесообразнее  проводить такие измерения и почему.

2.  Проанализировав  различные  способы  определения  площади  фигуры, сравните результаты измерений  (табл.  I  и 2) и укажите:

а) в каких случаях следует применять тот или иной  способ;
б) какой  из  способов  определения  площади  фигуры  является  наиболее точным;
в) как  повысить  точность измерений,  которые проводятся  с помощью  па­летки.

3  Сделайте вывод, в котором укажите, что именно вы измеряли, для чего вам могут пригодиться навыки,  полученные при выполнении этой работы.

Дополнительное задание

Определите  площадь  вашей  ладони  и  сравните  ее  с  площадью  ладони одного из членов вашей семьи.

Физика. 7 класс: Учебник / Ф. Я. Божинова, Н. М. Кирюхин, Е. А. Кирюхина. — X.: Издательство «Ранок», 2007. — 192 с.: ил.

Содержание урока
 конспект урока и опорный каркас
 презентация урока
 интерактивные технологии 
 акселеративные методы обучения

Практика
 тесты, тестирование онлайн
 задачи и упражнения 
 домашние задания
 практикумы и тренинги
 вопросы для дискуссий в классе

Иллюстрации
 видео- и аудиоматериалы
 фотографии, картинки 
 графики, таблицы, схемы
 комиксы, притчи, поговорки, кроссворды, анекдоты, приколы, цитаты

Дополнения
 рефераты
 шпаргалки 
 фишки для любознательных 
 статьи (МАН)
 литература основная и дополнительная
 словарь терминов

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 замена устаревших знаний новыми 

Только для учителей
 календарные планы
 учебные программы
 методические рекомендации  
 обсуждения

 Идеальные уроки-кейсы

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: