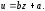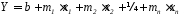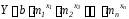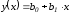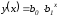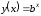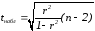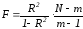построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
§ 9 ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЁ ГРАФИК
1. Преобразование уравнения ах + by + с = 0 к виду у = kx + m
Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 8, при всей его чёткости и определённости математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: сначала ах1 + by + с = 0, затем ах2 + by + с = 0? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим.
Рассмотрим сначала уравнение Зх — 2у + 6 = 0 (см. пример 2 из § 8), т. е. 2у = Зх + 6.
Умножив обе части уравнения на ½ получим …
Впрочем, тот же результат мы получили бы, если обе части исходного уравнения почленно разделили на 2. Обычно предпочитают в подобных случаях говорить не об умножении, а о почленном делении обеих частей уравнения на одно и то же число.
Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем у = 9. Видите, как легко и быстро найдены точки (0; 3), (-2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 8.
Точно так же уравнение 5х — 2у = 0 (см. пример 4 из § 
Из этого уравнения можно найти решения (0; 
Рассмотрим теперь указанные преобразования в общем виде.
Случаи, когда в уравнении ах + by + с = 0 коэффициенты а и b равны нулю, мы рассмотрели в § 8. Там же мы отметили, что в случае, когда а Ф О, b = 0, графиком уравнения является прямая, параллельная оси у.
Рассмотрим случай, когда b ≠ 0. Имеем ах + by + с = 0; (1) bу = -ах – с;
Введя обозначения … получаем у = kx + m.
Таким образом, линейное уравнение (1) с двумя переменными х и у в случае, когда b ≠ 0, можно преобразовать к виду у = kx + m (2) где k, m — числа (коэффициенты).
Это частный вид линейного уравнения. Зная, чему равен х, по правилу у = kx + m всегда можно найти, чему равен у. Будем называть уравнение (2) линейной функцией.
С помощью уравнения (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например, у = 2х + 3. Тогда:
если х = 0, то у = 3;
если х = 1, то у = 5;
если х = -1, то у = 1;
если х = 3, то у = 9 и т. д.
Обычно эти результаты оформляют в виде таблицы:
Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3 соответственно в точках х = 0, х = 1, х = -1, х = 3.
В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаём одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.
Частным случаем теоремы 1 из § 8 является следующая теорема.
ТЕОРЕМА 2. Графиком линейной функции у = kx + m является прямая.
ПРИМЕР 1. Построить график линейной функции у = 2х + 3.
Решение: Составим таблицу:
х I 0 I 1
У I 3 I 5
Построим на координатной плоскости хОу точки (0; 3) и (1; 5) и проведём через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 34).
Замечание. В русском языке часто один и тот же объект называют по-разному, например: «дом», «здание», «сооружение», «коттедж», «особняк», «барак», «хибара», «избушка». В математическом языке ситуация примерно та же. Скажем, равенство с двумя переменными у = kx + m, где k, m — конкретные числа, можно назвать линейной функцией, можно назвать линейным уравнением с двумя переменными х и у (или с двумя неизвестными x и у), можно назвать формулой, можно назвать соотношением, связывающим х и у, можно, наконец, назвать зависимостью между хну. Это неважно, главное — понимать, что во всех случаях речь идёт о математической модели у = kx + m.
2. Линейные функции как математические модели реальных ситуаций
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции. Приведём примеры.
Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Если пройдёт х дней, то количество у угля на складе (в тоннах) выразится формулой у = 500 + ЗОх. Таким образом, линейная функция у = ЗОх + 500 есть математическая модель ситуации.
Теперь нетрудно установить, что:
- при х = 2 имеем у = 560 (в уравнение у = ЗОх + 500 подставили х = 2 и получили у = 560);
- при х = 4 имеем у = 620;
- при х = 10 имеем у = 800.
Вторая ситуация. На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Здесь математической моделью ситуации является линейная функция у = 500 — ЗОх. С помощью этой модели нетрудно ответить на вопрос задачи:
- если х = 2, то у = 440 (в уравнение у = 500 — ЗОх подставили х = 2 и получили у = 440);
- если х = 4, то у = 380;
- если х = 10, то у = 200.
Третья ситуация. Турист проехал на автобусе 15 км от пункта А до пункта В, а затем продолжил движение в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от пункта А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы?
Математической моделью ситуации является линейная функция у = 15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи:
- если х = 2, то у = 23 (в уравнение у = 15 + 4х подставили х = 2 и получили у = 23);
- если х = 4, то у = 31;
- если х = 6, то у = 39.
Итак, в каждой из рассмотренных ситуаций математической моделью служит линейная функция. Но (внимание!), строго говоря, все три составленные модели не совсем точны, они не учитывают тех ограничений на переменную, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная х может принимать только значения 1, 2, 3, …, поскольку х — число дней. Следовательно, уточнённая математическая модель первой ситуации выглядит так:
у = 500 + ЗОх, где х — натуральное число.
Вторую ситуацию необходимо уточнить условием у > 0. Это значит, что независимая переменная х, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3, …, 16. Действительно, если х = 16, то по формуле у = 500 — ЗОх находим у = 500 — 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придётся прекратить. Следовательно, уточнённая математическая модель второй ситуации выглядит так:
у = 500 — ЗОх, у > 0 или у = 500 — ЗОх, где х = 1, 2, 3, …, 16.
В третьей ситуации независимая переменная х теоретически может принять любое неотрицательное значение (х = 0, х = 2, х = 3,5 и т. д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было принять разумные ограничения для х, скажем, 0 < х < 6 (т.е. турист идёт не более 6 ч).
Напомним, что геометрической моделью нестрогого двойного неравенства 0 < х < 6 служит отрезок [0; 6] координатной прямой (рис. 35). Значит, уточнённая модель третьей ситуации выглядит так: у = 15 + 4х, где х принадлежит отрезку [0; 6].
Условимся вместо фразы «х принадлежит множеству X» писать х е X (читают: «элемент х принадлежит множеству X», е — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается. Множество натуральных чисел обычно обозначают буквой N. Значит, вместо фразы «х — натуральное число» мы можем использовать соотношение х е N.
Если линейную функцию у = kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового множества X, то пишут у = kx + m, х ∈ Х.
А теперь запишем более точные математические модели для рассмотренных выше трёх ситуаций.
- Первая ситуация: у = 500 + ЗОх, х е N.
- Вторая ситуация: у = 500 — ЗОх, х е {1, 2, 3, …, 16}.
- Третья ситуация: у = 15 + 4х, х е [0; 6].
3. Построение графика линейной функции на заданном промежутке
Построить график линейной функции:
Решение: а) Составим таблицу для линейной функции у = -2х + 1:
х | -3 | 2
y I 7 I -3
Построим на координатной плоскости хОу точки (-3; 7) и (2; -3) и проведём через них прямую линию. Это график уравнения у = -2х + 1. Далее выделим отрезок, соединяющий построенные точки (рис. 36). Этот отрезок и есть график линейной функции у = -2х + 1, где х е [-3; 2].
Обычно говорят, что мы построили график линейной функции у = -2х + 1 на отрезке [-3; 2].
б) Чем отличается этот пример от предыдущего? Линейная функция та же (у = -2х + 1), значит, и графиком её служит та же прямая. Но — будьте внимательны! — на этот раз х е (-3; 2), т. е. значения х = -3 и х = 2 не рассматриваются, они не принадлежат интервалу (-3; 2). Как мы отмечали концы интервала на координатной прямой? Светлыми кружочками (рис. 39), об этом мы говорили в § 5. Точно так же и точки (-3; 7) и (2; -3) придётся отметить на чертеже светлыми кружочками. Это будет напоминать нам о том, что берутся лишь те точки прямой у = -2х + 1, которые лежат между точками, отмеченными кружочками (рис. 37). Впрочем, иногда в таких случаях используют не светлые кружочки, а стрелки (рис. 38). Это непринципиально: главное — понимать, о чём идёт речь.
ПРИМЕР 3. На координатной прямой отмечены точки А(-4), В(-3). Найти наибольшее и наименьшее значения линейной функции у = х/2 + 4 на отрезке [0; 6].
Решение: Составим таблицу для линейной функции. Построим на координатной плоскости хОу точки (0; 4) и (6; 7) и проведём через них прямую — график линейной функции
Нам нужно рассмотреть эту линейную функцию не целиком, а на отрезке [0; 6], т. е. для х е [0; 6]. Соответствующий отрезок графика выделен на чертеже. Обратим внимание, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 — это и есть наибольшее значение линейной функции у = х/2 + 4 на отрезке [0; 6]. Обычно используют такую запись:
Замечаем, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке 40 части прямой, равна 4 — это и есть наименьшее значение линейной функции у — iх + 4 на отрезке [0; 6]. Обычно используют такую запись:
Ответ: унаиб = 7, унаим = 4.
ПРИМЕР 4. Найти унаиб и унаим для линейной функции у = -1,5х + 3,5:
- а) на отрезке [1; 5];
- б) на интервале (1; 5);
- в) на полуинтервале [1; 5);
- г) на луче [0; +оо);
- д) на луче (~°°; 3].
Решение
Составим таблицу для линейной функции. Построим на координатной плоскости хОу точки (1; 2) и (5; -4) и проведём через них прямую (рис. 41—45). Выделим на построенной прямой часть, соответствующую значениям х из отрезка [1; 5] (рис. 41), из интервала (1; 5) (рис. 42), из полуинтервала [1; 5) (рис. 43), из луча [0; +°°) (рис. 44), из луча (~°°; 3] (рис. 45).
а) С помощью рисунка 41 нетрудно сделать вывод, что унаиб = 2 (этого значения линейная функция достигает при х = 1), а унаим = -4 (этого значения линейная функция достигает при х = 5).
б) В отличие от предыдущего случая, оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, из рассмотрения исключены (рис. 42). Среди остальных точек графика нет ни точки с наименьшей ординатой, ни точки с наибольшей ординатой. Значит, ни наибольшего, ни наименьшего значений на заданном интервале у данной линейной функции нет.
в) С помощью рисунка 43 заключаем, что унаиб 2 (как и в первом случае), а наименьшего значения у линейной функции нет (как и во втором случае).
г) унаиб = 3,5 (этого значения линейная функция достигает при х = 0), а унаим не существует (рис. 44).
д) унаим = -1 (этого значения линейная функция достигает при х — 3), а унаиб не существует (рис. 45).
4. Свойства линейной функции
ПРИМЕР 5. Построить график линейной функции у = 2х — 6. С помощью графика ответить на следующие вопросы:
а) при каком значении х будет у = 0;
б) при каких значениях х будет у > 0;
в) при каких значениях х будет у < 0?
Решение: Составим таблицу для линейной функции у = 2х — 6:
Через точки (0; -6) и (3; 0) проведём прямую — график линейной функции у = 2х — 6 (рис. 46).
- а) у = 0 при х = 3. График пересекает ось х в точке х = 3, это и есть точка с ординатой у — 0.
- б) у > 0 при х > 3. В самом деле, если х > 3, то соответствующая часть прямой расположена выше оси х, значит, ординаты соответствующих точек прямой положительны.
- в) у < 0 при х < 3. В самом деле, если х < 3, то соответствующая часть прямой расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны.
Обратите внимание, что в этом примере мы с помощью графика решили:
- а) уравнение 2х — 6 = 0 (получили х = 3);
- б) неравенство 2х — 6 > 0 (получили х > 3);
- в) неравенство 2х — 6 < 0 (получили х < 3).
Рассмотрим график линейной функции, изображённый на рисунке 47, а. Если двигаться по этому графику слева направо, то ординаты точек графика всё время увеличиваются, мы как бы «поднимаемся в горку». В таких случаях математики употребляют термин возрастание и говорят так: если к > 0, то линейная функция у = kx + m возрастает.
Рассмотрим график линейной функции, изображённый на рисунке 47, б. Если двигаться по этому графику слева направо, то ординаты точек графика всё время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин убывание и говорят так: если k < 0, то линейная функция у = kx + m убывает.
ПРИМЕР 6. На рисунке 48 изображён график движения автомобиля между пунктами 1 и 2. По оси t отмечено время (в часах), по оси S — расстояние до пункта 1. Требуется охарактеризовать весь процесс движения словами.
Решение: Точка А соответствует началу движения. До пункта 2 автомобиль доехал за 1 1/3 ч — об этом можно судить по абсциссе точки D. Пройденное расстояние равно 50 км — об этом можно судить по ординате точки D. Значит, можно вычислить скорость движения автомобиля: v = 50 : 4/3 = 37,5 км/ч.
На участке графика DE ордината постоянна, т. е. расстояние от пункта 1 не менялось. Это значит, что автомобиль не двигался (стоял в пункте 2). Причём он стоял в промежутке от 1^ ч до 2-| ч (это абсциссы точек D и Е). Остановка длилась, таким образом, 1 ч 20 мин.
На обратный путь после остановки автомобиль потратил столько же времени, сколько на путь от 1 до 2, значит обратно он ехал с той же скоростью.
Вопросы для самопроверки
- Что такое линейная функция?
- Что является графиком линейной функции?
- Сколько точек достаточно взять для построения графика линейной функции?
- Опишите процесс построения графика линейной функции у = 2х + 3, где х е [0; 2]. Что изменится, если х е (0; 2)?
- Дана линейная функция у = kx + m, х е X, где X — некоторый числовой промежуток. Что такое унаим, унаиб?
- Дано: у = 2х + 3, х е [0; +оо). Найдите, если возможно, унаим, унаиб. Что изменится, если х е (0; +оо)? если х е (—оо; 0]? если X € (-оо; 0)?
- Как с помощью графика линейной функции у = kx + m, где k Ф 0, решить: а) уравнение kx + m = 0; б) неравенство kx + m > 0; в) неравенство kx + m < 0?
- В каком случае линейная функция возрастает, а в каком — убывает? Как об этом можно судить по графику линейной функции?
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Свойства линейной функции
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
у=2х – 1=2×0 – 1= –1;
у=2х – 1=2×3 – 1= 5.
Вписываем в таблицу значения у:
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
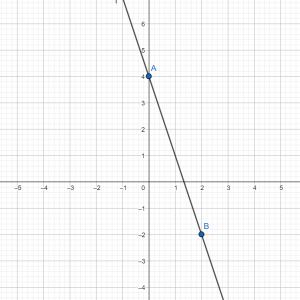
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
Пример №3
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
Задание OM1106o
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор
Задание OM1103o
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 6.1k
Пусть
приближающая функция имеет вид: F(x,
a,
c)=ax+b
Тогда
частные производные:
Составим
систему вида (3):
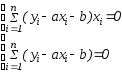
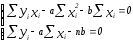
Разделим
каждое уравнение системы (2) на n
и приведем ее к следующему виду:
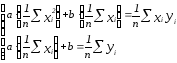
Обозначим:
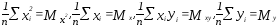
Тогда
система имеет вид:
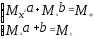
Коэффициенты
этой системы – числа, которые легко
вычисляются в каждой конкретной задаче
по формулам (3) через значения
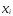
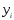
Решив
последнюю систему (4), получаем конкретный
вид линейной функции y=ax+b.
7.4.2. Квадратная регрессия (параболическая функция).
В
этом случае приближенная функция имеет
вид:

Частная
производная
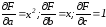
Составим
систему вида:
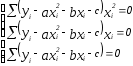
Приведем
подобные слагаемые аналогично методу
получения методу линии регрессии и
обозначим
тогда
система примет вид:
Решение
последней системы дает значения
параметров a,
b,
c
для приближенной функции в виде параболы.
7.4.3. Степенная функция (геометрическая регрессия).
Уравнение
линии степенной функции иногда еще
называют геометрической регрессией.
Покажем, что нахождение приближенных
функций с двумя параметрами F(x,
a,
b)
в виде элементарных функций может быть
сведено к нахождению параметров линейной
функции.
Будем
искать функцию в виде:
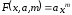
Предположим,
что любые
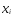
0 и
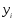
0.
Прологарифмируем
(1):
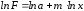
Т.
к.
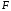
то
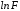
Введем
новую переменную
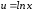
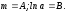
Тогда
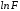
функция от
Тогда
(2) примет вид:
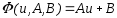
т.
е. задача свелась к отысканию приближающей
функции в виде линейной.
Практически
при нахождении приближающей степенной
функции необходимо выполнить следующие
действия:
-
По
исходной таблице составить новую,
прологарифмировав значения х и у. -
По
новой таблице найти параметры А и В для
линейной функции вида (3). -
Используя
введенные обозначения (*), найти а и m
и подставить в выражение (1).
7.4.4. Показательная функция.
Пусть
приближающая функция имеет вид:
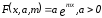
Прологарифмируем
это равенство:
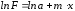
Обозначения
те же:
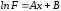
Т.
о. алгоритм построения приближающей
функции следующий:
-
Прологарифмировать
значения функции у в исходной таблице. -
Для
новой таблицы с исходными значениями
и новыми
найти параметры А и В.
-
Используя
введенное обозначение
найти а иm,
подставить их в формулу показательной
функции.
7.4.5. Дробно – линейная функция.
Пусть
приближающая функция имеет вид: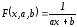
Перепишем
равенство следующим образом:
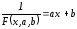
Отсюда следует, что для нахождения
параметрова
и b
необходимо в исходной таблице значения
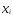
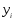
по полученной таблице найти приближенную
функциюax+b.
7.4.6.
Логарифмическая функция.
Пусть
приближающая функция имеет вид: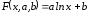
Для
перехода к линейной функции достаточно
сделать подстановку:
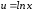
Практически:
-
в
исходной таблице логарифмируем значения
;
-
по
новым значениям аргумента и исходным
значениям
находятся параметры а иb,
которые подставляют в новое равенство.
6.4.7.
Гипербола.
Если
точечный график, построенный по исходной
таблице, дает ветвь гиперболы, то
приближающую функцию можно искать в
виде:
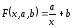
Выполнив
подстановку 
получим: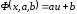
Практический
алгоритм:
-
в
исходной таблице значения аргумента
следует заменить обратными числами и
найти для новой таблицы приближающую
функцию в виде линейной; -
полученные
параметры а и b
подставить в исходную формулу.
7.4.8.
Дробно-рациональная функция.
Пусть
приближающая функция будет иметь вид:
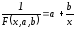
Имеем:
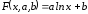
Алгоритм
вычисления:
-
в
исходной таблице значения х
и у
заменяем обратными величинами:
и
;
-
по
новой таблице строим функцию вида
-
найденные
значения а
и b
будут искомыми.
7.5.6
Проведение регрессионного анализа
средствами MS Excel.
Расчет
параметров линейной регрессии с
использованием функции ЛИНЕЙН.
Для
линейной аппроксимации в Excel
существует функция ЛИНЕЙН(изв.
зн. Y,
изв. зн. X,
константа, статистика)
она возвращает массив значений описывающих
кривую вида:
где
изв.
зн. Y
– это известные значения функции
изв.
зн. X
– это известные значения аргументов
константа
–
определяет чему должно равняться b,
если константа
имеет значение ЛОЖЬ
то b
полагается равным 1,
иначе b
вычисляется обычным образом.
статистика
– если значение равно ИСТИНА
то будет представлена дополнительная
регрессионная статистика, если ЛОЖЬ
то нет.
Для
получения линейной регрессионной
зависимости, с выводом всей статистической
информации следует выделить диапазон
A54:С58,
нажать клавишу F2,
и ввести формулу =ЛИНЕЙН(P2:P38;N2:O38;1;1),
после
окончания ввода формулы нажать комбинацию
клавиш Ctrl+Shift+Enter
так как данная функция возвращает массив
значений. В результате в данных ячейках
будет полная статистическая информация:
|
Линейная |
||
|
0.645 |
0.176 |
229.123 |
|
0.039 |
0.038 |
94.969 |
|
0.963 |
115.657 |
#Н/Д |
|
441.156 |
34 |
#Н/Д |
|
11802358 |
454805 |
#Н/Д |
Полученные
числа имеют следующий смысл:
|
mn |
mn-1 |
… |
b |
|
Sen |
Sen-1 |
… |
Seb |
|
R2 |
Sey |
||
|
F |
Df |
||
|
Ssreg |
Ssresid |
Se
– стандартная ошибка для коэффициента
m
Seb
– стандартная ошибка для свободного
члена b
R2
– коэффициент детерминированности,
который показывает как близко уравнение
описывает исходные данные. Чем ближе
он к 1, тем больше сходится теоретическая
зависимость и экспериментальные данные.
Sey
– стандартная ошибка для y
F
– критерий Фишера определяет случайная
или нет взаимосвязь между зависимой и
независимой переменными
Df
– степень свободы системы
Ssreg
– регрессионная сумма квадратов
Ssresid
– остаточная сумма квадратов
Аналогичным
образом построим линейную регрессионную
зависимость при аргументе Константа
равном 0, в диапазоне E54:G58,
введя формулу =ЛИНЕЙН(P2:P38;N2:O38;0;1):
|
Линейная |
||
|
0.728 |
0.146 |
0 |
|
0.021 |
0.039 |
#Н/Д |
|
0.9980 |
123.365 |
#Н/Д |
|
8925.124 |
35 |
#Н/Д |
|
2.7E+08 |
532666 |
#Н/Д |
Расчет
параметров линейной регрессии с
использованием инструмента Регрессия
надстройки Пакет
анализа.
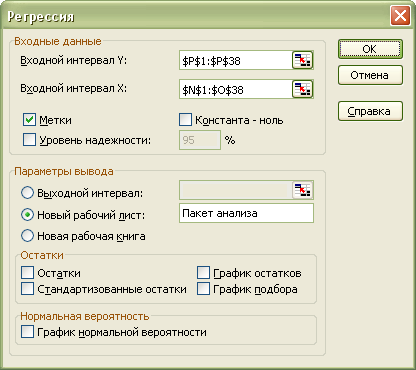
Для
проведения регрессионного анализа
выберем пункт меню Данные/Анализ
данных/Регрессия.
Откроется следующее диалоговое окно:
После
заполнения полей ввода нажимаем кнопку
OK
и получаем следующие результаты:
|
Регрессионная |
|
|
Множественный |
0.981 |
|
R-квадрат |
0.963 |
|
Нормированный |
0.961 |
|
Стандартная |
115.657 |
|
Наблюдения |
37 |
|
Дисперсионный |
|||||
|
df |
SS |
MS |
F |
Значимость |
|
|
Регрессия |
2 |
11802358 |
5901179 |
441.156 |
4.79E-25 |
|
Остаток |
34 |
454805.4 |
13376.63 |
||
|
Итого |
36 |
12257163 |
|
Коэффициенты |
Стандартная |
t |
P |
Нижние |
Верхние |
Нижние |
Верхние |
|
|
Y |
229.123 |
94.969 |
2.413 |
0.021 |
36.122 |
422.123 |
36.122 |
422.123 |
|
X2 |
0.176 |
0.038 |
4.597 |
0.000 |
0.098 |
0.255 |
0.098 |
0.255 |
|
X5 |
0.645 |
0.039 |
16.336 |
1.15E-17 |
0.565 |
0.726 |
0.565 |
0.726 |
Результаты,
полученные при расчете с использованием
инструмента Регрессия
надстройки Пакет
анализа,
совпали с результатами, полученными
при помощи функции ЛИНЕЙН
при аргументе Константа
имеющем значение ИСТИНА.
Расчет
параметров экспоненциальной регрессии
с использованием функции ЛГРФПРИБЛ.
Для
экспоненциальной аппроксимации в Excel
существует функция ЛГРФПРИБЛ(изв.
зн. Y,
изв. зн. X,
константа, статистика)
она возвращает массив значений описывающих
кривую вида:
изв.
зн. Y
– это известные значения функции
изв.
зн. X
– это известные значения аргументов
константа
–
определяет чему должно равняться b,
если константа
имеет значение ЛОЖЬ
то b
полагается равным 1,
иначе b
вычисляется обычным образом.
статистика
– если значение равно ИСТИНА
то будет представлена дополнительная
регрессионная статистика, если ЛОЖЬ
то нет.
Для
получения экспоненциальной регрессионной
зависимости, с выводом всей статистической
информации следует выделить диапазон
I54:K58,
нажать клавишу F2,
и ввести формулу =ЛГРФПРИБЛ(P2:P38;N2:O38;1;1),
после
окончания ввода формулы нажать комбинацию
клавиш Ctrl+Shift+Enter
так как данная функция возвращает массив
значений. В результате в данном диапазоне
будет получена полная статистическая
информация:
|
Экспоненциальная |
||
|
1.0002 |
1.00007 |
1030.47 |
|
1.9E-05 |
0.000 |
0.046 |
|
0.940 |
0.057 |
#Н/Д |
|
266.115 |
34 |
#Н/Д |
|
1.702 |
0.109 |
#Н/Д |
Полученные
числа имеют следующий смысл:
|
mn |
mn-1 |
… |
b |
|
Sen |
Sen-1 |
… |
Seb |
|
R2 |
Sey |
||
|
F |
Df |
||
|
Ssreg |
Ssresid |
Se
–
стандартная ошибка для коэффициента m
Seb
– стандартная ошибка для свободного
члена b
R2
– коэффициент детерминированности,
который показывает как близко уравнение
описывает исходные данные. Чем ближе
он к 1, тем больше сходится теоретическая
зависимость и экспериментальные данные.
Sey
– стандартная ошибка для y
F
–
критерий Фишера определяет случайная
или нет взаимосвязь между зависимой и
независимой переменными
Df
– степень свободы системы
Ssreg
– регрессионная сумма квадратов
Ssresid
– остаточная сумма квадратов
Аналогичным
образом построим экспоненциальную
регрессионную зависимость при аргументе
Константа
равном 0, в диапазоне M54:O58,
введя формулу =ЛГРФПРИБЛ(P2:P38;N2:O38;0;1):
|
Экспоненциальная |
||
|
1.003 |
0.99913 |
1 |
|
0.000244 |
0.000447 |
#Н/Д |
|
0.969 |
1.429 |
#Н/Д |
|
542.226 |
35 |
#Н/Д |
|
2215.263 |
71.496 |
#Н/Д |
Определение
модели наиболее точно описывающей
фактические данные.
|
Зависимость |
Вид |
R2 |
|
Линейная |
|
0.963 |
|
Линейная |
|
0.998 |
|
Экспоненциальная |
|
0.940 |
|
Экспоненциальная |
|
0.969 |
Моделью
наиболее точно описывающей фактические
данные является линейная модель вида
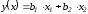
так как для нее коэффициент
детерминированностиR2
имеет наибольшее значение.
Оценка
значимости коэффициентов модели и
адекватности модели.
Оценка
качества модели по критериям Стьюдента
и Фишера будет проводиться путём
сравнения расчетных значений с табличными.
Для
оценки качества модели по критерию
Стьюдента фактическое значение этого
критерия (tнабл)
сравнивается
с критическим значением tкр
которое берется из таблицы значений t
с учетом заданного уровня значимости
(α
= 0.05)
и числа степеней свободы (n
— 2).
Если
tнабл
> tкр,
то
полученное значение коэффициента парной
корреляции признается значимым.
Критическое
значение при
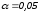
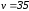
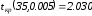
|
Критерий |
|||
|
Фактор |
tнабл |
tкр |
Значимость |
|
Х2 |
7.568 |
2.030 |
существенна |
|
Х5 |
20.913 |
2.030 |
существенна |
Проверим
значимость коэффициента детерминации,
используя F‑критерий
Фишера.
Вычислим
статистику F
по формуле:
где:
m
= 3
– число параметров в уравнении регрессии;
N
= 37
– число наблюдений в выборочной
совокупности.
Математической
моделью статистического распределения
F-статистики
является распределение Фишера с

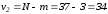
этой статистики при
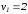
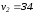
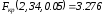
|
Критерий |
||
|
Fрасч |
Fкр |
Уравнение |
|
8916.383 |
3.276 |
адекватно |
Таким
образом, модель
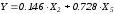
общей дисперсии признака Y.
Это указывает на то, что подобранная
модель является адекватной. 1.6. Расчет
прогнозных значений и суммы квадратов
отклонений.
Введем
в ячейку Q2
формулу =$F$54*N2+$E$54*O2
(расчет прогнозных значений), затем
скопируем ее в ячейки Q3:Q38.
В ячейку R2
формулу =(P2-Q2)^2
(расчет суммы квадратов отклонений),
затем скопируем ее в ячейки R3:R38,
и подсчитаем сумму полученных значений
в ячейке R39.
|
X2 |
X5 |
Y |
y(x) |
(Y |
|
605.1 |
2063.2 |
1626.7 |
1589.7 |
1367.523 |
|
620.1 |
2143.7 |
1602.5 |
1650.5 |
2303.318 |
|
914 |
2447.7 |
1880.7 |
1914.5 |
1144.709 |
|
862.1 |
2406.4 |
1982.7 |
1876.9 |
11189.53 |
|
958.4 |
2592.9 |
2037 |
2026.7 |
106.5821 |
|
1488.9 |
2698 |
2193.9 |
2180.4 |
182.342 |
|
1231.5 |
2529.7 |
2152.1 |
2020.4 |
17335.88 |
|
1429.6 |
2644.9 |
2227 |
2133.1 |
8814.026 |
|
1679.5 |
2793.7 |
2344.4 |
2277.8 |
4436.216 |
|
1326.2 |
2669.2 |
2341.7 |
2135.8 |
42415.15 |
|
1456.8 |
2845 |
2211.9 |
2282.7 |
5014.463 |
|
2523.6 |
2990.5 |
2629.8 |
2543.9 |
7377.384 |
|
846 |
2659.8 |
2017.5 |
2059.0 |
1722.637 |
|
923.8 |
2636.6 |
2009.4 |
2053.4 |
1939.955 |
|
1173.3 |
2943.1 |
2260 |
2312.8 |
2792.24 |
|
1156.7 |
2890.9 |
2400.1 |
2272.4 |
16298.85 |
|
1450.2 |
3051.5 |
2508.1 |
2432.0 |
5784.146 |
|
1845.2 |
3249 |
2684.1 |
2633.3 |
2581.453 |
|
1566.4 |
3052.6 |
2736.6 |
2449.8 |
82275.65 |
|
1729.7 |
3349.7 |
2824.5 |
2689.8 |
18152.31 |
|
1987.3 |
3456.3 |
2880.2 |
2804.9 |
5676.928 |
|
1902.7 |
3731.2 |
2812.9 |
2992.6 |
32297.9 |
|
1839.1 |
3517.8 |
2704.2 |
2828.0 |
15336.69 |
|
3953.7 |
3823.1 |
3224.2 |
3358.1 |
17922.28 |
|
1351.2 |
3482.9 |
2584.7 |
2731.6 |
21584.07 |
|
1185.3 |
3347.6 |
2466.7 |
2609.0 |
20246.66 |
|
1715.5 |
3585.4 |
2928.3 |
2859.2 |
4768.047 |
|
1536.4 |
3678.3 |
3036.4 |
2900.8 |
18389.81 |
|
1823.1 |
3801.6 |
3021.1 |
3032.3 |
124.6986 |
|
2452.1 |
4002.1 |
3237.6 |
3269.8 |
1034.273 |
|
2076.6 |
3990.3 |
3247.1 |
3206.5 |
1647.633 |
|
2129.2 |
4212 |
3436.9 |
3375.5 |
3767.099 |
|
2502.7 |
4154.2 |
3472.8 |
3387.8 |
7220.377 |
|
2238.7 |
4322.7 |
3504.1 |
3472.0 |
1028.291 |
|
2417.6 |
4623.1 |
3357.1 |
3716.7 |
129321.2 |
|
3838.4 |
4817.9 |
4034.7 |
4065.3 |
937.7363 |
|
1468.6 |
4632 |
3450.4 |
3585.0 |
18128.14 |
|
∑ |
532666.2 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вспомним, что такое график функции:
Графиком функции называется множество точек плоскости, абсциссы которых равны значениям аргумента $x$, а ординаты – соответствующим значениям функции $y$.
Как мы уже выяснили, график линейной функции представляет из себя прямую линию.
Построение графиков
Для его построения нет необходимости находить координаты более двух точек. То есть, чтобы построить график линейной функции, достаточно подставить в заданную формулу всего два значения $x$.
Значит, нужно:
-
Подставить в функцию 2 любых значения $x$ и получить соответствующие значения $y$.
-
Мы получили координаты 2 точек. Отметим их на координатной плоскости.
-
Проведём через эти 2 точки прямую линию.
Пример
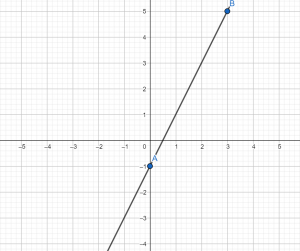
Построим график функции $y=2x+1$
Для удобства состоим таблицу значений $x$ и $y$.
| Переменная | Значение 1 | Значение 2 |
|---|---|---|
| $x$ | ||
| $y$ |
Какие $x$ взять? Удобно брать небольшие числа, например $0$ и $1$
| Переменная | Значение 1 | Значение 2 |
|---|---|---|
| $x$ | $color{#3D68EB}0$ | $color{#ED7858}1$ |
| $y$ |
Теперь нужно посчитать $y$. Подставляем по очереди 2 значения $x$ в нашу функцию:
$x=color{#3D68EB}0$
$y=2x+1$
$y=2 cdot 0 + 1 = color{#253f8d}1$
$x=color{#ED7858}1$
$y=2x+1$
$y=2 cdot 1 + 1 = color{#eb3d3d}3$
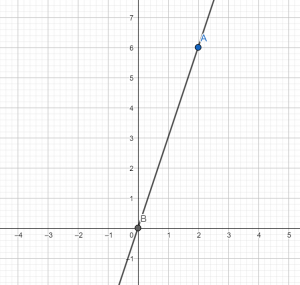
Вписываем полученные значения в таблицу и отмечаем точки:
| Переменная | Значение 1 | Значение 2 |
|---|---|---|
| $x$ | $color{#3D68EB}0$ | $color{#ED7858}1$ |
| $y$ | $color{#253f8d}1$ | $color{#eb3d3d}3$ |
Проводим через эти точки прямую линию. График готов.
Доведите навык до совершенства с помощью тренажёра построения графиков линейной функции.






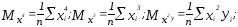
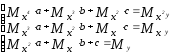

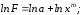
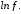
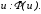
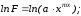
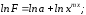
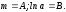
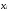 и новыми
и новыми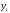 найти параметры А и В.
найти параметры А и В.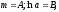 найти а иm,
найти а иm,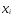 ;
;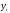 находятся параметры а иb,
находятся параметры а иb,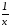 и
и ;
;