Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
-
Коэффициент (a) можно найти с помощью следующих фактов:
— Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.
— Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
— Аналогично с (a<-1), только график вытянут вниз.
— Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.
— Аналогично (a∈(-1;0)), только ветви направлены вниз.
-
Парабола пересекает ось y в точке (c).
-
(b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) — абсциссы (икса) вершины параболы:
(x_в=-frac{b}{2a})
(b=-x_вcdot 2a)
Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).
(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)
Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:
(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1); (x_2=frac{2+4}{2}=3).
Ответ: (3).
2 способ – находим формулу по точкам
Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:
-
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример: -
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).
(begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})
-
Решаем систему.
Пример:(begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})
Вычтем из второго уравнения первое:
(0=9a-b)
(b=9a)Подставим (9a) вместо (b):
(begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
(begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
(2=-2a)
(a=-1)Найдем (b):
(b=-9)
Подставим в первое уравнение (a):
(5=20+c)
(c=-15).Получается квадратичная функция: (y=-x^2-9x-15).
Пример (ЕГЭ):

Решение:
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:
(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})
(begin{cases}8=a-b+4\2=a+b+4 end{cases})
(begin{cases}4=a-b\-2=a+b end{cases})
Сложим 2 уравнения:
(2=2a)
(a=1)
Подставим во второе уравнение:
(-2=1+b)
(b=-3)
Получается:
(g(x)=x^2-3x+4)
Теперь найдем точки пересечения двух функций:
(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)
Теперь можно найти ординату второй точки пересечения:
(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)
Ответ: (22).
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа — вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
-
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
-
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз. -
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц. -
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
(y=x^2-10x+25-4)
(y=x^2-10x+21)
Готово.
Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
-
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
-
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
-
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
-
Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).
-
(f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)
Смотрите также:
Как найти k и b по графику линейной функции?
С квадратными уравнениями мы уже встречались в курсе алгебры (7)-го класса.
Квадратное уравнение — это уравнение второй степени. Общий вид квадратного уравнения
ax2+bx+c=0
, где (а, b, с) могут быть любыми числами и
a≠0
,
Применяя знания о функциях и их графиках, которые нам известны, мы можем решать некоторые квадратные уравнения. Рассмотрим (5) графических способов решения квадратного уравнения
x2−2x−8=0
.
Первый способ
Построим график функции
x2−2x−8=0
.
1. Имеем: (a = 1), (b = -2),
x0=−b2a=1,y0=f(1)=12−2−8=−9
. Значит, вершиной параболы служит точка ((1; -9)), а осью параболы является прямая (x = 1).
2. Возьмём на оси (x) две точки, симметричные относительно оси параболы, например, точки (x = -2) и (x = 4). Имеем (f(-2) = f(4) = 0). Построим на координатной плоскости точки ((-2; 0)) и ((4; 0)).
3. Построим параболу по точкам ((-2; 0)), ((1; -9)), ((4; 0)).
Корни уравнения
x2−2x−8=0
— это первые координаты точек, в которых функция равна нулю (то есть в которых график пересекает ось (х)); поэтому имеем решение:
x1=−2;x2=4
.
Второй способ
Запишем уравнение в другом виде
x2=2x+8
. Рассмотрим функции в левой и правой частях уравнения
y=x2;y=2x+8
. В одной системе координат построим их графики и найдём точки пересечения графиков:
Получили две точки:: (C(- 2; 4)) и (D(4; 16)). Решением уравнения будут первые координаты точек (C) и (D), имеем:
x1=−2;x2=4
.
Преобразуем уравнение к виду
x2−8=2x
. Построим в одной системе координат графики функций:
y=x2−8;y=2x
и определим точки их пересечения:
Получили две точки: (C(-2; — 4)) и (D(4; 8)). Решением уравнения будут первые координаты точек (C) и (D), то есть
x1=−2;x2=4
.
Четвёртый способ
Преобразуем уравнение к виду
x2−2x+1−9=0
и далее
x2−2x+1=9→x−12=9
.
Построим в одной системе координат параболу
y=x−12
, прямую (y = 9) и определим точки их пересечения:
Получили две точки: (C(-2; 9)) и (D(4; 9)). Решением уравнения будут первые координаты точек (C) и (D), поэтому
x1=−2;x2=4
.
Пятый способ
Так как (x=0) не является корнем уравнения, то разделим левую и правую части на (x):
x−2−8x=0;x−2=8x.
Рассмотрим функции в левой и правой частях уравнения
y=8x
, (y = x — 2) и определим точки их пересечения:
Получили две точки: (A (-2; -4)) и (B(4; 2)). Решением уравнения будут первые координаты точек (A) и (B), следовательно,
x1=−2;x2=4
.
Здравствуйте. В данной статье я попытаюсь показать вам возможные способы решения квадратных уравнений с помощью графиков.
Допустим, надо решить уравнение х2 ‒ 2х ‒ 3 = 0. На этом примере мы рассмотрим варианты решения квадратного уравнения графически.
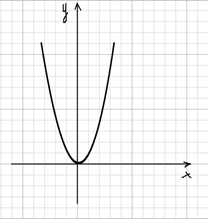
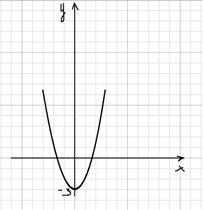
1) Можно представить наше уравнение в виде х2 = 2х + 3. Далее построим в одной системе координат графики функций у = х2 и у = 2х + 3. График у = х2 представлен на рисунке 1, а оба графика на рисунке 2.
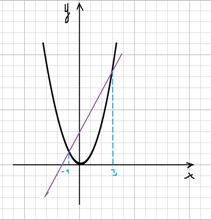
Графики пересекаются в двух точках, наше уравнение имеет решение х = – 1 и х = 3.
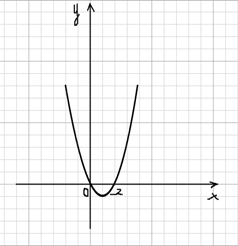
2) А ведь можно представить уравнение и по — другому, например х2 ‒ 2х = 3 и построить в одной системе координат графики функций у = х2 ‒ 2х и у =3. Вы их можете увидеть на рисунках 3 и 4. На рисунке 3 изображен график у = х2 ‒ 2х, а на рисунке 4 оба графика у = х2 ‒ 2х и у =3.
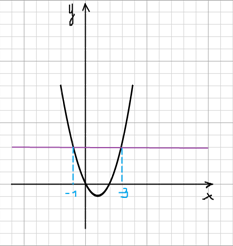
Как мы видим, эти два графика так же пересекаются в двух точках, где х = -1 и х = 3. Значит ответ: — 1; 3.
3) Есть и другой вариант представления этого уравнения х2 ‒ 3 = 2х. И снова строим графики функций у = х2 ‒ 3 и у = 2х в одной системе координат. Первый у = х2 ‒ 3 на рисунке 5 и оба графика на рисунке 6.
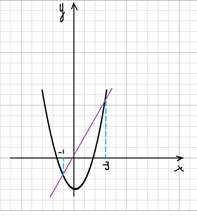
Они также пересекаются в двух точках, в которых х = -1 , х = 3.
Ответ: — 1; 3.
4) Можно построить параболу у = х2 ‒ 2х ‒ 3.
Вершина параболы х0 = — b/2а = 2/2=1, у0 = 12 ‒ 2·1 ‒ 3 = 1 – 2 – 3 = ‒ 4. Это точка (1; ‒ 4). Тогда наша парабола симметрична относительно прямой х =1. Если взять две точки симметричные относительно прямой х = 1 например: х = — 2 и х = 4, то мы получим две точки через которые проходят ветви графика.
Если х = -2, то у =(- 2)2 ‒ 2( -2) ‒ 3 = 4 + 4 – 3 = 5.
Аналогично х =4, у = 42 ‒ 2 · 4 ‒ 3= 16 – 8 – 3 = 5. Полученные точки ( -2; 5); (1; 4) и (4; 5) отмечаем в на плоскости и проводим параболу рисунок 7.
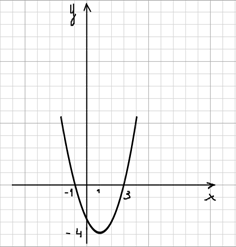
Парабола пересекает ось абсцисс в точках – 1 и 3. Это и есть корни уравнения х2 ‒ 2х ‒ 3 = 0.
Ответ: – 1 и 3.
5) А можно выделить квадрат двучлена:
х2 ‒ 2х ‒ 3= 0
(х2 ‒ 2х + 1) ‒1 ‒ 3= 0
(х -1)2 — 4 = 0
(х — 1)2 = 4
Затем построить в одной системе координат графики функций у = (х — 1)2 и у = 4. Первый график у = (х — 1)2 на рисунке 8, а оба графика у = (х — 1)2 и у = 4 на рисунке 9.
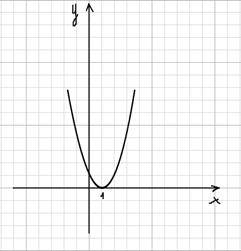
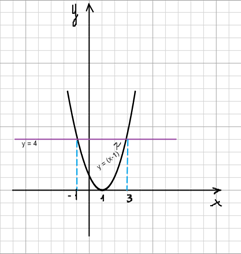
Они также пересекаются в двух точках, в которых х = -1 , х = 3.
Ответ: — 1; 3.
6) Так как х = 0 не является корнем уравнения х2 ‒ 2х ‒ 3 = 0 (иначе выполнялось бы равенство 02 – 2· 0 –3 = 0), то можно все члены уравнения разделить на х. В результате мы получим уравнение х – 2 – 3/х = 0. Перенесем 3/х вправо и получаем уравнение х – 2 = 3/х Тогда можно построить в одной системе координат графики функций у = 3/х и у = х – 2.
На рисунке 10 изображен график функции у = 3/х, а на рисунке 11 оба графика функций у = 3/х и у = х – 2.
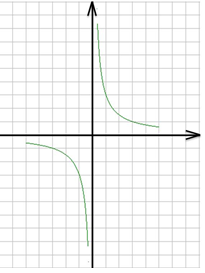
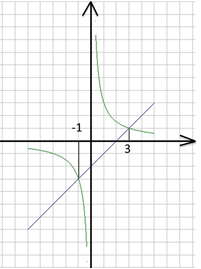
Они также пересекаются в двух точках, в которых х = -1 , х = 3.
Ответ: — 1; 3.
Если вы были внимательны, то обратили внимание, что каким бы образом вы не представили бы уравнение в виде двух функций, у вас всегда будет один и тот же ответ (разуметься, что вы не допустите ошибок при переносе выражений из одной части уравнения в другую и при построении графиков). Поэтому, решая графически уравнение, выбирайте способ представления функций графики которых вам легче построить. И еще одно замечание если корни уравнения не целые числа, то ответ получится не точным.
Репетитор Валентина Галиневская.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Инфоурок
›
Алгебра
›Презентации›Графическое решение квадратных уравнений
Графическое решение квадратных уравнений
Скачать материал

Скачать материал








Описание презентации по отдельным слайдам:
-
1 слайд
Графическое решение
Квадратных уравнений.
Выполнила: Темникова А.Е.
Педагог математики -
2 слайд
Немного истории
Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений.
Диофант Александрийский,
Аль- Хорезми.
Евклид Омар Хайям
Решали уравнения
геометрическими и
графическими способами -
3 слайд
Для графического решения квадратного уравнения представьте его в одном из видов:
ax2 + bx +c = 0
ax2 = -bx – c
ax2 + c = — bx
a(x + b/2a)2 = ( 4ac — b2 )/4a
Квадратное уравнение имеет вид ax2 + bx + c = 0 -
4 слайд
Алгоритм графического решения квадратных уравнений
Ввести функцию f(x), равную левой части и g(x) , равную правой части
Построить графики функций y=f(x) и y=g(x) на одной координатной плоскости
Отметить точки пересечения графиков
Найти абсциссы точек пересечения, сформировать ответ -
5 слайд
Способы графического решения квадратного уравнения
ах² + bх + с = 0Способ поcтрое-
ния параболы y=ах² +bx+c
Способ поcтрое-
ния прямой
у= bx+c и параболы у = ах²
Способ поcтрое-
ния прямой
у= bx и параболы у = ах²+с
Способ выделе-ния полного квадрата
I
II
III
(a)
(b)
Способ поcтрое-
ния прямой
у= с и параболы у = ах²+ bx
(в) -
6 слайд
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт». У. У. Сойер.
-
7 слайд
Графическое решение квадратного уравнения
Иллюстрация на одном примере
-
8 слайд
Алгоритм решения квадратного уравнения графическим способом
Способ 1
Построить график функции y=ax2+bx+c
Найти точки пересечения графика с осью абсцисс -
9 слайд
Решить уравнение
1 способ
Построим график функции у =
График-парабола, а=1>0,ветви вверх.
Вершина ( )=-
Х ο = 1
(1; -4)-вершина
3. Ось параболы
4. Дополнительные точки:
х
у
1
-4
0
-1
2
3
0
-3
-3
0
Корнями уравнения являются
абсциссы точек пересечения графика с осью х, т.е. где у=0.
Значит, корни уравнения -1 и 3. Проверка устно. Ответ: -1; 3.
-1
1
-1
3
х
3
о
у -
10 слайд
Алгоритм построения параболы
найти координаты вершины; провести ось параболы;
отметить на оси абсцисс две точки, симметричные относительно оси параболы; найти значения функции в этих точках;
провести параболу через полученные точки. -
11 слайд
Пусть f(x)= x2 – 2x -3 и g(x) =0
а = 1>0, ветви вверх
Координаты вершины x۪۪ ο =-b/2a; x۪۪ ο =1 .
y ο = 1² — 2 – 3 = -4; y ο = -4; ( 1; -4)
Найти точки абсциссы которых симметричны относительно х=1
Построить по таблице график y=x2 -2x -3Примеры графического решения квадратных уравнений
3
-1
Решение уравнения x2-2x –3=0
Корни уравнения равны абсциссам точек пересечения параболы с осью ОХу=x2 – 2x -3
-
12 слайд
Графический способ решения квадратных уравнений
Квадратное уравнение имеет два равных корня
Квадратное уравнение не имеет корней
Квадратное уравнение имеет два различных корня -
13 слайд
Алгоритм решения квадратного уравнения графическим способом
Способ 2(а)
Построить графики функции y=ax2 и у = bx+ с
Найти абсциссы точек пересечения графиков. -
14 слайд
x2 – 2x – 3 =0
Представим в виде x2 = 2x +3
Пусть f(x)=x2 и g(x)=2x +3
Построим на одной координатной плоскости графики функций
y=x2 и y= 2x + 3
3
-1
Корни уравнения абсциссы точек пересечения параболы с прямой -
15 слайд
2 способ
Преобразуем уравнение
к виду
Построим в одной системе координат графики функций
-это парабола
-это прямая
х
у
0
1
3
5
3
-1
3
Корнями уравнения являются
абсциссы точек пересечения: -1 и 3
Корнями уравнения являются
абсциссы точек пересечения: -1 и 3 -
16 слайд
4 x2 – 4x + 1 =0
Представим в виде 4×2 = 4x -11). Построим графики функций:
у = 4 x2 , у = 4x — 1
2). Строим параболу у = 4 x2
а = 4, ветви вверх
хο = — ; хο= 0; ; уο= 0.По шаблону строим параболу
3). Строим прямую у = 4x — 1-1
0
1
3
1
0,5
Корнем уравнения является
абсцисса точки пересечения: 0,5
-1
-1
у
х -
17 слайд
Алгоритм решения квадратного уравнения графическим способом
Способ 2 (b)
Преобразовать уравнение к виду
ax2+с = bx
Построить:
параболу y = ax2+с и прямую y = bx
Найти абсциссы точек пересечения
графиков функции. -
18 слайд
x2 – 2x – 3 =0
Представим в виде x2 –3 = 2x
Пусть f(x)=x2 –3 и g(x)=2x
Построим на одной координатной плоскости графики функций
y=x2 –3 и y =2x-1
3
Корни уравнения абсциссы точек пересечения параболы с прямой
y=x2 –3
y =2x -
19 слайд
x2 – 4x + 5 =0
Представим в виде x2 +5 = 4x
Пусть f(x)=x2 +5 и g(x)=4x
Построим на одной координатной плоскости графики функций
y=x2 +5 и y =4x
Точек пересечения параболы с прямой нет
Ответ: корней нет
y=x2 +5
y =4x
y
x
о -
20 слайд
Алгоритм решения квадратного уравнения графическим способом
Способ 2(в)
Построить графики функции
y=ax2 + bx и у = с
Найти абсциссы точек пересечения графиков. -
21 слайд
x2 – 2x – 3 =0
Представим в виде x2 – 2x = 3
Пусть f(x)= х² — 2х и g(x)=3
Построим на одной координатной плоскости графики функций
y= х² — 2х и y=3
-13
Корни уравнения абсциссы точек пересечения параболы с прямой
y=3
y= х² — 2х
y
х
о
2
-1
3 -
22 слайд
Алгоритм решения квадратного уравнения графическим способом
Способ 3
(выделение полного квадрата)
Преобразовать уравнение к виду
a(x+l)2 = m
Построить:
параболу y = a(x+l)2 и прямую y = m
Найти абсциссы точек пересечения графиков функций. -
23 слайд
Выделение квадрата двучлена.
x2 – 2x + 1 = 3 + 1
( x –1)2=4.
x2 – 2x = 3
( x –1)2 — 4 = 0
( x –1)2 — 2² = 0
( x –1 – 2) ( x –1 + 2 ) = 0
( x –3 ) ( x + 1 ) = 0
x –3 = 0
x + 1 = 0
x = 3
x = — 1 -
24 слайд
x2 – 2x – 3 =0
Представим в виде (x –1)2=4
Пусть f(x)= (x – 1)2 и g(x)=4
Построим на одной координатной плоскости графики функций
y= (x –1)2 и y=4
-13
Корни уравнения абсциссы точек пересечения параболы с прямой
y=4
y= (x –1)2 -
25 слайд
Решите графически уравнение
Группа А
Группа С
Группа В
х² + 2х – 8= 0
4х² — 8х + 3= 0
3х² + 2х – 1= 0 -
26 слайд
Сколько нам открытий чудных готовит просвещения дух?
-
27 слайд
Решить графически уравнение
-
28 слайд
Как решить уравнение?
Построить график квадратичной функции и абсциссы точек пересечения параболы с осью x будут являться корнями уравнения.
Выполнить преобразование уравнения, рассмотреть функции, построить графики этих функций, установить точки пересечения графиков функций, абсциссы которых и будут являться корнями уравнения. -
29 слайд
Решить графически уравнение
-
30 слайд
Построить график функции
-
31 слайд
Построить график функции
-
32 слайд
Корни уравнения: абсциссы точек пересечения графиков функций
-
33 слайд
Построить график функции
Корни уравнения:
точки пересечения
параболы с осью ОХ -
34 слайд
Решить графически уравнение
Корни уравнения:
точки пересечения
параболы и прямой -
35 слайд
Решить графически уравнение
Корни уравнения:
точки пересечения
параболы и прямой -
36 слайд
Итог
Познакомились:
с графическим методом решения квадратных уравнений;
с различными способами графического решения квадратных уравнений.
закрепили знания по построению графиков различных функций. -
37 слайд
Заключительное слово учителя:
«Чем больше и глубже вам удастся усвоить азы математики и научиться пользоваться ее методами, тем дальше и быстрее вы сумеете продвинуться в использовании математических средств в той области деятельности, которой займетесь после школы» -
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 265 343 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 30.03.2017
- 557
- 0
- 30.03.2017
- 543
- 0
Рейтинг:
4 из 5
- 30.03.2017
- 10518
- 187
- 30.03.2017
- 410
- 0
- 30.03.2017
- 600
- 0
- 30.03.2017
- 366
- 0
- 30.03.2017
- 1312
- 3
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Настоящий материал опубликован пользователем Grigorenko Alexandra Evgenevna. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 5 месяцев
- Подписчики: 2
- Всего просмотров: 21387
-
Всего материалов:
20
Home » 8 класс » Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?
Урок: как построить параболу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Парабола — это график функции описанный формулой ax2+bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:
1 ) Формула параболы y=ax2+bx+c,
если а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;
2 ) Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;
3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax2+bx+c=0;
Виды уравнений:
a) Полное квадратное уравнение имеет вид ax2+bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax2+bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax2+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);
Как решать квадратные уравнения посмотреть тут.
4) Найти несколько дополнительных точек для построения функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
И так теперь на примере разберем все по действиям:
Пример №1:
y=x2+4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)2+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x2+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b2-4ac=16-12=4
x=(-b±√(D))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2
х -4 -3 -1 0
у 3 0 0 3
Подставляем вместо х в уравнение y=x2+4x+3 значения
y=(-4)2+4*(-4)+3=16-16+3=3
y=(-3)2+4*(-3)+3=9-12+3=0
y=(-1)2+4*(-1)+3=1-4+3=0
y=(0)2+4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2
Пример №2:
y=-x2+4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1<0.
a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)2+4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x2+4x=0
Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x2+4x значения
y=02+4*0=0
y=-(1)2+4*1=-1+4=3
y=-(3)2+4*3=-9+13=3
y=-(4)2+4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2
Пример №3
y=x2-4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0)2-4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x2-4=0
Неполное квадратное уравнение вида ax2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x2=4
x1=2
x2=-2
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x2-4 значения
y=(-2)2-4=4-4=0
y=(-1)2-4=1-4=-3
y=12-4=1-4=-3
y=22-4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0
Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.




























































