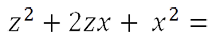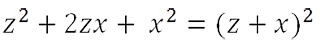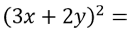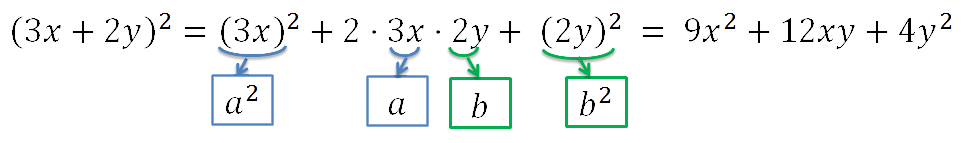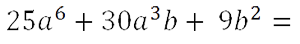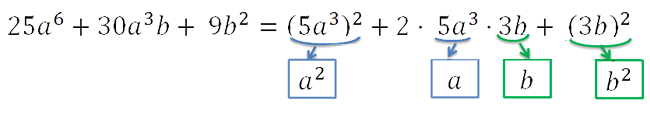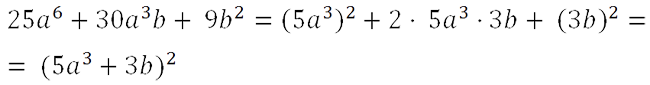В данной публикации мы рассмотрим одну из формул сокращенного умножения, а именно, квадрат суммы. Также разберем примеры решения задач для закрепления изложенного материала.
- Формула квадрата суммы
-
Доказательство формулы
- Арифметическое
- Геометрическое
- Примеры задач
Формула квадрата суммы
Квадрат суммы слагаемых a и b равняется квадрату a плюс удвоенное произведение a и b плюс квадрат b.
(a + b)2 = a2 + 2ab + b2
Выражение может быть представлено и в обратном порядке:
a2 + 2ab + b2 = (a + b)2
Доказательство формулы
Арифметическое
Представим формулу в виде произведения двух одинаковых скобок (другими словами, умножим выражение на само себя):
(a+b)(a+b).
Теперь раскроем скобки согласно арифметическим правилам и получаем:
(a+b)(a+b) = a2 + ab + ba + b2 = a2 + 2ab + b2.
Геометрическое
Для того, чтобы доказать формулу геометрически, изобразим квадрат, который поделен с помощью двух отрезков на четыре части таким образом, что получились:
- два квадрата с разной длиной стороны (a или b);
- 2 прямоугольника с одинаковой длиной (a) и шириной (b).
Площадь большого квадрата равна (a + b)2 и, одновременно, сумме площадей фигур, из которых состоит:
Sкв. = (a + b)2 = a2 + ab + ab + b2 = a2 + 2ab + b2.
Примеры задач
Задание
Чему равен квадрат суммы (2x + 4y3)2?
Решение
Воспользуемся формулой сокращенного умножения:
(2x + 4y3)2 = (2x)2 + 2 ⋅ 2x ⋅ 4y3 + (4y3)2 = 4x2 + 16xy3 + 16y6
Примечание:
Формулу можно использовать для быстрых расчетов в уме, например:
- 632 = (60 + 3)2 = 602 + 2 ⋅ 60 ⋅ 3 + 32 = 3600 + 360 + 9 = 3969.
- 942 = (90 + 4)2 = 902 + 2 ⋅ 90 ⋅ 4 + 42 = 8100 + 720 + 16 = 8836.
В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители:
вынесение общего множителя за скобки
и
способ группировки.
В этом уроке мы рассмотрим еще один способ разложения многочлена на множители — применение формул сокращённого умножения.
Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все
формулы сокращённого умножения себе на небольшую
шпаргалку.
Применение квадрата суммы для разложения многочлена на множители
Вспомним, как выглядит формула квадрата суммы.
(a + b)2 =
a2 + 2ab + b2
Важно помнить, что любая формула сокращённого умножения действует и в обратную сторону.
a2 + 2ab + b2 =
(a + b)2
Рассмотрим многочлен. Требуется разложить его на множители, используя формулу квадрата суммы.
Обратите внимание, что многочлен «z2 + 2zx + x2» напоминает правую часть формулы
«a2 + 2ab + b2»
,
только вместо «a» стоит «z»,
а на месте «b» стоит «x».
Используем для многочлена «z2 + 2zx + x2» формулу квадрата суммы.
Рассмотрим другой пример. Необходимо возвести в квадрат многочлен.
Используем формулу квадрата суммы. Только вместо «a» у
нас будет «3x», а вместо
«b» —
«2y».
Часто возводят многочлен в квадрат следующим образом:
Это неверно! Для возведения многочлена в квадрат необходимо использовать формулу сокращенного умножения:
(a + b)2 =
a2 + 2ab + b2.
Рассмотрим пример сложнее. Требуется разложить многочлен на множители.
В этом многочлене не так очевидно, что будет являться в формуле
«a2»,
«2ab»,
а что «b2».
Представим многочлен в виде «a2 + 2ab + b2».
После необходимых преобразований видно, что в многочлене
«25а6 + 30а3b + 9b2»
на месте
«a» стоит
«5a3»,
а на месте «b»
—
«3b». Используем формулу квадрата суммы и решим пример до конца.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
9 сентября 2016 в 18:11
Нурторе Амангелды
Профиль
Благодарили: 0
Сообщений: 1
Нурторе Амангелды
Профиль
Благодарили: 0
Сообщений: 1
Тема: Метод выделения полного квадрата. Правила
Здравствуйте… Можете помочь почему мы взяли именно 52 для приминения формулы (a-b)2 ?
Вот задача:
x 2 – 10x – 11 =
x 2 – 10x + 5 2 – 5 2 – 11 =
(x 2 – 10x + 5 2) – 36 =
(x – 5) 2 – 6 2 =
(x – 5 – 6) (x – 5 + 6) =
(x – 11) (x + 1) .
0
Спасибо
Ответить
22 сентября 2016 в 11:16
Ответ для Нурторе Амангелды
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Взяли 52 для того чтобы дополнить до формулы разность квадратов, а именно (a ? b)2 = a2 ? 2ab + b2 . В формуле уже имеется начало формулы. 10x=2ab = 2 · x · b. Отсюда следует, что b=5. Дополняем до формулы и отнимаем этоже значение, чтобы выражение в целом не изменилось.
0
Спасибо
Ответить
Формулы сокращённого умножения
- Разложение формул сокращенного умножения
- Неполный квадрат суммы
- Неполный квадрат разности
При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.
Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.
a2 + b2 = (a + b)2 — 2ab — сумма квадратов;
a2 — b2 = (a + b)(a — b) — разность квадратов;
(a + b)2 = a2 + 2ab + b2 — квадрат суммы;
(a — b)2 = a2 — 2ab + b2 — квадрат разности;
a3 + b3 = (a + b)(a2 — ab + b2) — сумма кубов;
a3 — b3 = (a — b)(a2 + ab + b2) — разность кубов;
(a + b)3 = a3 + 3a2b + 3ab2 + b3 — куб суммы;
(a — b)3 = a3 — 3a2b + 3ab2 — b3 — куб разности.
Обратите внимание, что a
и b
в формулах сокращённого умножения могут быть как числами, так и выражениями.
Разложение формул сокращенного умножения
Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.
Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:
a2 + b2 = (a + b)2 — 2ab.
Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)2 — 2ab = (a + b)(a + b) — 2ab = a2 + ab + ab + b2 — 2ab = a2 + b2.
Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:
a2 — b2 = (a + b)(a — b).
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)(a — b) = a2 — ab + ab — b2 = a2 — b2.
Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(a + b)2 = a2 + 2ab + b2.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2.
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:
(a — b)2 = a2 — 2ab + b2.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)2 = (a — b)(a — b) = a2 — ab — ab + b2 = a2 — 2ab + b2.
Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:
a3 + b3 = (a + b)(a2 — ab + b2).
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)(a2 — ab + b2) = a3 — a2b + ab2 + a2b — ab2 + b3 = a3 + b3.
Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:
a3 — b3 = (a — b)(a2 + ab + b2).
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a — b)(a2 + ab + b2) = a3 + a2b + ab2 — a2b — ab2 — b3 = a3 — b3.
Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:
(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)3 = (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3.
Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:
(a — b)3 = a3 — 3a2b + 3ab2 — b3.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)3 = (a — b)(a — b)2 = (a — b)(a2 — 2ab + b2) = a3 — 2a2b + ab2 — a2b + 2ab2 — b3 = a3 — 3a2b + 3ab2 — b3.
Неполный квадрат суммы
Выражение:
a2 + 2ab + b2
это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:
a2 + ab + b2,
которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности
Выражение:
a2 — 2ab + b2
это квадрат разности, который также называется полным квадратом разности относительно выражения:
a2 — ab + b2,
которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.
Уральская
область
Теректинский
район
Аксуаткая общая
средняя
общеобразовательная
школа
Учитель
математики
Тукжанова
Салтанат Ербулатовна
Урок: алгебра 7б
Тема: Формулы
квадрата суммы и квадрата разности двух выражений.
Цель:
— получение и
использование формул для возведения в квадрат суммы и разности двух выражений.
— выработка умений
самостоятельно применять знания, умения и навыки
— воспитание воли,
трудолюбия, самостоятельности.
Оборудование: дидактический материал; проектор; слайды; компьютер.
Структура урока:
1.
Организационный момент
Вступительное
слово учителя (на экране)
«Дорогу осилит идущий, а математику — мыслящий»
Довести до сведения учащихся
ход урока, показать перспективу изучения темы. Отметить отсутствующих.
2.Проверка
домашней работы.
Математический
диктант.
Найдите квадраты
выражений: а; -2; 3ав; 3ху.
Найдите
произведение 2х и 4у?
Что называют
многочленом?
Что называют
одночленом?
Какие слагаемые
называются подобными?
3. Изучение
нового материала.
Квадрат суммы двух выражений. Умножение многочлена на
многочлен в некоторых случаях удается выполнить короче. Равенства, выражающие
эти частные случаи умножения, называются формулами сокращенного умножения.
Возведем в квадрат сумму двух выражений а и
b:
(а+b)2=(a+b)(a+b)=a2+ab+ab+b2
т.е. мы доказали справедливость тождества:
(а+b)2 =a2+2ab+b2 (1)
Тождество (1) называют формулой квадрата суммы двух выражений.
Отсюда получим правило:
Квадрат суммы двух выражений равен квадрату первого
выражения, плюс удвоенное произведение первого и второго выражений, плюс
квадрат второго выражения.
Квадрат разности двух выражений. Теперь возведем в квадрат разность а-b
(а-b)2=(a-b)(a-b)=a2-ab-ab+b2=
a2-2ab+b2
Значит,
(а-b)2= a2-2ab+b2 (2)
Квадрат разности двух выражений равен квадрату
первого выражения, минус удвоенное произведение первого и второго выражений,
плюс квадрат второго выражения.
С помощью формул
(1) и (2) удобно вычислять квадраты чисел, на несколько едениц отличающихся от
«круглого» числа.
Формулы (1) и (2) часто используются и в
обратном порядке, т.е. в виде:
a2+2ab+b2 = (а+b)2
a2-2ab+b2 = (а-b)2
3. Закрепление
нового материала:
4. Контрольные
вопросы
— Напишите формулу квадрата суммы и дайте ее формулировку
словами.
— Напишите формулу квадрата разности и дайте ее
формулировку словами.
5.Задание на дом: §1, №332(1,3,5,7,9), 338(2,4,6)
6. Подведение
итогов урока
Проводится с помощью кубика- экзаменатора, на каждой грани которого
записан номер примера. Вызванный к доске ученик подбрасывает кубик и
комментирует выпавшую ему на верхней грани часть формулы. Записывает это на
доске вместе с многочленом, в который можно преобразовать данный квадрат
двучлена Задания для кубика – экзаменатора
Разложение на множители
Представим в виде многочлена квадрат суммы некоторых выражений a и b: (a + b)^2 = (a + b)*(a + b) = a^2 + a*b + a*b + b^2 = a^2 + 2*a*b + b^2
Формула квадрата суммы и квадрата разности
Получившееся тождество называют формулой квадрата суммы двух выражений. Итак, квадрат суммы двух выражений равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения. Выражение a^2 + 2*a*b + b^2 называют полным квадратом суммы выражений a и b.
Теперь представим в виде многочлена разность выражений a и b:
(a b)^2 = (a b)*(a b) = a^2 a*b a*b + b^2 = a^2 2*a*b + b^2
Это тождество называют формулой квадрата разности двух выражений a и b. Кстати, из него следует, что (a b)^2 = (b a)^2 . Выражение a^2 2*a*b + b^2 называют полным квадратом разности выражений a и b.
Квадрат суммы нескольких слагаемых
Представляя в виде многочлена выражения (a + b + c)^2, (a + b + c + d)^2, получаем:
(a + b + c)^2 = a^2 + (b+c)^2 + 2*a*(b+c) = a^2 + b^2 + c^2 + 2*a*b + 2*b*c + 2*a*c;
(a + b + c + d)^2 = (a+b)^2 + (c+d)^2 =2*(a+b)*(c + d) = a^2 + b^2 + c^2 + d^2 + 2*a*b + 2*a*c + 2*a*d + 2*b*c + 2*b*d + 2*c*d
Существует общая формулировка для возведения в квадрат суммы нескольких слагаемых, а именно: квадрат суммы нескольких выражений равен сумме квадратов этих выражений и удвоенных произведений каждых двух из этих выражений.
Если в формуле квадрата суммы двух выражений или в формуле квадрата разности двух выражений поменять местами левую и правую части, то получается формула, позволяющая раскладывать на множители трёхчлены вида a^2 + 2*a*b + b^2 и a^2 + 2*a*b + b^2.
Способ нахождения квадрата большого числа
Иногда формулу квадрата суммы или квадрата разности используют для того, чтобы найти квадрат некруглого числа. Например, требуется найти квадрат числа 199. Представим 199 как 200 1 и возведём эту разность в квадрат:
(200 1)^2 = 200^2 2*200*1 + 1^2 = 40000 400 + 1 = 39601, то есть 199^2 = 39601.
Рассмотрим пример. Разложите многочлен на множители:
8x^2 24*x + 10
Решение. Вынесем за скобки общий множитель 2:
8x^2 24x + 10 = 2*(4x^2 12x + 5)
Представим 5 как 9 4:
2(4x^2 12x + 5) = 2(4x^2 12x + 9 4)
Представим 9 как 3^2, а 4 как 2^2:
2(4x^2 12x + 9 4) = 2(4×2 12x + 3^2 4^2)
Разложим на множители полный квадрат разности 2х и 3:
2(4x^2 12x + 3^2 4^2) = 2((2x 3)^2 2^2)
Разложим разность квадратов выражений 2x 3 и 2 по формуле сокращённого умножения:
2((2x 3)^2 2^2) = 2((2x 3) 2)((2x 3) + 2) = 2(2x — 5)(2x 1)
Рассмотрим ещё один пример. Разложите многочлен на множители:
2x^2 + 28xy + 80y^2 + 36yz + 18z^2
Решение. Вынесем за скобки общий множитель 2:
2x^2 + 28xy + 80y^2 + 36yz + 18z^2 = 2(x^2 + 14xy + 40y^2 + 18yz + 9z^2)
В скобках выделим полный квадрат разности x 7y:
2(x^2 + 14xy + 40y^2 + 9y^2 — 9y^2 — 18yz — 9z^2) = 2((x^2 + 14xy + 49y^2) — 9y^2 — 18yz — 9z^2)
Представим его в виде квадрата двучлена:
2((x^2 + 14xy + 49y^2) — 9y^2 — 18yz — 9z^2) = 2((x + 7y)^2 — (9y^2 + 18yz + 9z^2))
Теперь выделим полный квадрат суммы 3y + 3z и представим его в виде квадрата двучлена:
2((x + 7y)^2 — (9y^2 + 18yz + 9z^2)) = 2((x + 7y)^2 — (3y + 3z)^2)
Теперь разложим разность квадратов в скобках по формуле разности квадратов:
2((x + 7y)^2 — (3y + 3z)^2) = 2(x + 7y + 3y + 3z)*(x + 7y — 3y — 3z) = 2(x + 10y + 3z)*(x + 4y — 3z).
Нужна помощь в учебе?
Предыдущая тема: Возведение в квадрат суммы и разности двух выражений: формулы и примеры
Следующая тема: Умножение разности двух выражений на их сумму: формулы и примеры
| Нравится | Нравится |