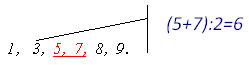Загрузить PDF
Загрузить PDF
Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.[1]
Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.[2]
Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.
-
1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
-
2
Для вычисления среднего значения понадобятся все числа данного набора данных.[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
-
3
Сложите все числа вашего набора данных.[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
-
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама
-
1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
-
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
-
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 22, 02, 22, 02, 02, и (-4)2 = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
-
4
Сложите квадраты значений, то есть найдите сумму квадратов.[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
-
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама
-
1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
-
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
-
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама
Об этой статье
Эту страницу просматривали 64 743 раза.
Была ли эта статья полезной?
Алгебра 7 класс. Что такое отклонение? например: 2,7,3,5,11,15
Дисперсией числового ряда называется среднее арифметическое квадратов отклонений от среднего арифметического.
Пусть есть некий ряд (значения некоторой случайной величины — скажем, возраст детей в семье): 2,7,3,5,11,15.
1) находим среднее арифметическое: (2+7+3+5+11+15) / 6= 7,17
2) находим среднее арифметическое квадратов отклонений:
(2-7,17)^2+(7-7,17)^2+(3-7,17)^2+(5-7,17)^2+(11-7,17)^2+(15-7,17)^2/6=
Дисперсия характеризует разброс — чем больше дисперсия, тем сильнее «разбросан» (варьируется) признак относительно центрального значения.
Как посчитать среднее значение, квадратическое отклонение и погрешность
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 24 человек(а).
Количество просмотров этой статьи: 62 795.
После сбора данных их нужно проанализировать. Обычно нужно найти среднее значение, квадратичное отклонение и погрешность. Мы расскажем вам, как это сделать.
- Например, 5 школьникам был предложен письменный тест. Их результаты (в баллах по 100 бальной системе): 12, 55, 74, 79 и 90 баллов.
- Среднее значение (μ) = Σ/N, где Σ сумма всех числовых значений, а N количество значений.
- Для вышеуказанного примера это квадратный корень из [((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27,4. (Обратите внимание, что если это выборочное среднеквадратическое отклонение, то делить нужно на N-1, где N количество значений.)
- Если в нашем примере 5 школьников, а всего в классе 50 школьников, и среднее отклонение, посчитанное для 50 школьников равно 17 (σ = 21), средняя погрешность = 17/кв. корень(5) = 7.6.
Метод вычисления отклонений каждого значения от среднего арифметического
Для вычисления отклонений всех чисел выполним следующие действия:
. Находим среднее арифметическое;
2. Для вычисления отклонение из данного набора чисел вычитаем среднее арифметическое.
Среднее арифметическое нескольких величин — это отношение суммы величин к их количеству.
Среднее арифметическое находится по формуле
(2)
(3)
Найти отклонений всех чисел от среднего арифметического.
Сумма чисел в массиве (2):
Вычисление отклонения (3):
Блок схема 2 — Вычисление отклонений каждого значения от среднего арифметического
Описание методов создания, уничтожения и синхронизации потоков, примененных в программе
Создание потоков
Для создания многопоточных приложений в C++Builder реализован абстрактный класс TThread.- абстрактный класс, который допускает создание отдельных потоков выполняющихся в приложении.
Создайте потомка класса TThread, чтобы представить выполняемый поток в многопоточном приложении.
Каждый новый экземпляр потомка TThread — новый поток выполнения.
Множество экземпляров, полученные от класса TThread, делает C++Builder многопоточным приложением.
__fastcall TMyThread:: TMyThread (bool CreateSuspended)
// B метод объекта Execute (), вставьте код, который должен выполняться, когда поток выполняется.
void __fastcall TMyThread:: Execute ()
// — — Place thread code here — —
Для получения безопасного доступа куправлению свойствами и методами VCL-объектов в потоке предусмотрен метод Synchronize ()
ResetEvent (FMain->g_BusyEvent [1]); // запрещаем переформирование массива(FMain->g_BusyEvent [0]); // запрещаем переформирование массива
>++;(Terminated) break; // прекратить извне поток
Synchronize (&Mon); // блокирует одновременный доступ к компоненту нескольких потоков
SetEvent (FMain->g_BusyEvent [0]); // разрешаем параллельную обработку(FMain->g_BusyEvent [1]); // разрешаем параллельную обработку
Синхронизация потоков
Синхронизации потоков основывается на использовании событий (event). Объект типа событие может принимать одно из двух состояний: активное или пассивное. Когда событие находится в активном состоянии, его видят многие потоки одновременно. В результате такой объект можно использовать для управления работой сразу многих потоков. В библиотеке VCL события представлены классом TEvent.
Метод CreatEvents (): Создает объект класса TEvent, представляющий объект события.
Метод ResetEvent (): Переводит объект события в пассивное состояние.
Метод SetEvent (): Переводит объект события в активное состояние.
WaitForSingleObject (): Заставляет ждать, пока другой поток или процесс не пошлют сигнал об активизации объекта событие.
Завершение потоков
Потоки могут быть запущены и остановлены сколько угодно раз в процессе их выполнения. Для временной остановки запущенного потока можно обратиться к методу потока suspend. Для продолжения выполнения приостановленного потока вызовите метод потока Resume. Вы можете использовать вложенные вызовы вышеперечисленных методов, т.к. метод Suspend увеличивает внутренний счетчик потока, a Resume уменьшает. Поток не будет выполняться до тех пор, пока счетчик не обратиться в ноль, т.е., если вы вызвали пять раз метод Suspend, а затем четыре раза Resume, вам понадобится еще один (пятый) вызов метода Resume для продолжения выполнения потока.
Выполнение потока автоматически завершается после завершения функции Execute () или закрытии приложения.
Чтобы занятая потоком память освобождалась при завершении потока надо установить FreeOnTerminate=false.
Урок по теории вероятностей и статистике в 7 классе
Тема «Отклонения. Дисперсия». 7-й класс
Цель: сформировать у учащихся представление о понятиях “отклонение” и “дисперсия” и навыки их применения в реальных статистических исследованиях
Задачи урока:
- образовательные – показать, что окружающий нас изменчивый мир можно описать математическими понятиями, числовыми показателями;
- развивающие– формировать современное мировоззрение и умение ориентироваться в изменчивом информационном мире;
- воспитательные – учить мыслить категориями, имеющими вероятностный характер, применять вводимые понятия в практической жизни.
Планируемые результаты:
- знать, что такое отклонение от среднего арифметического и дисперсия;
- уметь вычислять отклонения, квадраты отклонений и дисперсию на коротких наборах;
- уметь применять понятия квадратов отклонений и дисперсии при анализе реальных ситуаций;
Оборудование:
- мультимедийный проектор, экран.
Дидактические материалы:
- карточки с таблицами.
Ход урока
I. Организационный момент
Сообщить тему и цели урока. (Слайд 1).
II. Актуализация знаний учащихся
На предыдущих уроках мы рассмотрели так называемые средние характеристики числового ряда, позволяющие оценить его поведение “в среднем”. Повторим их определения и способы нахождения.
Слайд 2 – задание на повторение (комментарии учителя, проверка ответов учеников с помощью слайда).
Задание. Дан числовой набор.
|
Х |
1 |
2 |
3 |
5 |
8 |
100 |
Найти среднее арифметическое и медиану, определить, какая из характеристик лучше характеризует числовой набор и почему?
III. Изучение нового материала, формирование знаний, умений и навыков
Слайд 3 — характеристики числового ряда (комментарии учителя).
Средние характеристики числового ряда (среднее арифметическое, медиана), позволяют оценить поведение ряда “в среднем”. Но это не всегда наиболее полно характеризуют выборку. Чтобы получить полное представление о поведении числового ряда, помимо средних характеристик надо знать характеристики разброса, показывающие, насколько сильно значения ряда отличаются друг от друга, как сильно они разбросаны вокруг средних.
Рассмотрим следующий пример ( раздать карточки с таблицами, которых нужно заполнять по ходу урока)
Слайд 4-5 – задание 1 (комментарий учителя).
Международные спортивные игры «Дети Азии» получили свое начало в 1996 г. по инициативе первого Президента Республики Саха (Якутия) М.Е.Николаева и были посвящены 100-летию олимпийского движения. С тех пор они проводятся совместно с Олимпийским комитетом России, Росспортом, Министерством иностранных дел Министерством образования и науки Российской Федерации. Летом 2012 года будет V международная спортивная игра «Дети Азии».
Для участия в V международных спортивных играх «Дети Азии» нужно выбрать лучших футболистов республики. На одно место футболиста претендуют двое. Для каждого из них установили испытательный срок, в течение которого они должны были участвовать в отборных играх. Результаты спортсменов представлены в таблице
Вопрос: кого из футболистов предпочтительнее взять на спортивные игры?
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
Рассчитаем, сколько голов забил каждый из футболистов за 5 сезонов.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
|
Итого: |
100 |
100 |
Вывод: количество голов одинаково.
Рассчитаем, сколько голов в сезон забивал в среднем каждый футболист. Для этого найдём среднее арифметическое числовых наборов Х и Y.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
|
Итого: |
100 |
100 |
|
Среднее арифметическое |
20 |
20 |
Среднее арифметическое у обоих футболистов тоже одинаковое.
На данном примере мы увидели, что с помощью средних характеристик сравнение выполнить не всегда возможно.
Как поступить?
В данном случае критерием сравнения может выступать стабильность игры– у какого футболиста количество забитых им голов в сезон менее отличается друг от друга, тот играет стабильнее.
Если количество забитых в сезон голов сильно разнится, то в какой-то сезон футболист играет не в полную силу, забивает меньше голов, а в какой-то сезон навёрстывает упущенное, а это всегда сказывается на качестве игры.
Стабильность можно оценивать с помощью отклонений элементов числового набора от среднего значения (отклонение – это разность между числом из данного набора и средним арифметическим этого набора)
Слайд 6 – пример вычисления отклонений (комментарии учителя).
Отклонение – разность между средним значением и числом набора
Набор отклонений:
|
X — X |
-2 |
-4 |
0 |
2 |
4 |
Логично предположить, что чем меньше будет разброс (отклонения от среднего значения) – тем стабильнее играет футболист.
Но когда набор чисел велик, рассматривать отклонения практически неудобно, нужно описать разнообразие чисел в наборе одним числом.
Попробуем найти сумму отклонений.
Слайд 6 – пример вычисления суммы отклонений (комментарии учителя, вывод).
-2-4+0+2+4=0
В сумме получилось 0 (т.к. при вычислении “среднего разброса” часть отклонений входит в сумму со знаком “+”, часть со знаком “-” и в сумме всегда получается 0). Следовательно сумма отклонений не может нести информацию о разбросе.
Какой же выход?
Можно суммировать квадраты отклонений (они всегда неотрицательны).
Слайд 7 – пример вычисления квадратов отклонений (комментарии учителя)
Набор квадратов отклонений:
|
(X – X)² |
4 |
16 |
0 |
4 |
16 |
Сумма квадратов отклонений:
4+16+0+4+16 = 40
Чем меньше сумма квадратов отклонений, тем меньше разброс чисел относительно среднего значения, тем более стабилен набор.
Итак, рассчитаем сумму квадратов отклонений для нашего примера.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
|
Итого: |
100 |
100 |
|
Среднее арифметическое |
20 |
20 |
|
Сумма квадратов отклонений |
32 |
30 |
Вывод: второй футболист играет более стабильно, у него меньше сумма квадратов отклонений. Вероятно, тренер предпочтёт взять на соревнование его.
В данном примере футболисты играли одинаковое количество сезонов. А если они количество сезонов неодинаково?
Тогда стабильность игры каждого можно было бы оценить по величине среднего арифметического квадратов отклонений от среднего значения – дисперсии.
Слайд 8 – пример вычисления дисперсии (комментарии учителя).
Дисперсия — среднее арифметическое квадратов отклонений:
Dx= (4+16+0+4+16)/5 = 40/5 = 8
Дисперсия – характеристика разброса, мера стабильности.
Чем больше дисперсия, тем ниже стабильность
Рассмотрим следующий пример.
Слайд 9 – задание 2 (комментарии учителя).
(Ученикам открыть лист “Задание 2” файла с заданиями).
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
17 |
— |
|
2 |
21 |
17 |
|
3 |
20 |
20 |
|
4 |
16 |
18 |
|
5 |
15 |
21 |
|
6 |
19 |
14 |
Аналогично заданию 1 рассчитаем, сколько голов забил каждый футболист и сумму квадратов отклонений.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
17 |
— |
|
2 |
21 |
17 |
|
3 |
20 |
20 |
|
4 |
16 |
18 |
|
5 |
15 |
21 |
|
6 |
19 |
14 |
|
Итого: |
108 |
90 |
|
Среднее арифметическое |
18 |
18 |
|
Сумма квадратов отклонений |
28 |
30 |
Т.к. футболисты играли разное количество сезонов, рассчитаем и сравним дисперсии числовых наборов X и Y.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
17 |
— |
|
2 |
21 |
17 |
|
3 |
20 |
20 |
|
4 |
16 |
18 |
|
6 |
19 |
14 |
|
Итого: |
108 |
90 |
|
Среднее арифметическое |
18 |
18 |
|
Сумма квадратов отклонений |
28 |
30 |
|
Дисперсия |
4,6 |
6 |
Вывод: первый футболист играет стабильнее второго.
3. Самостоятельная практическая работа.
Слайд 10 — задание 3.
С 28 марта по 2 апреля в Южной Якутии пройдёт II Спартакиада зимних видов спорта Республики Саха (Якутия). Примут её опять Алдан и Нерюнгри.
Для участия в II Спартакиаде зимних видов спорта Республики Саха (Якутия)нужно выбрать лучших лыжников района. На одно место претендуют двое. Для каждого из них установили испытательный срок, в течение которого они должны были участвовать в отборных соревнованиях. Результаты спортсменов на 10 км.представлены в таблице
Вопрос: кого из спортсменов предпочтительнее взять на спартакиаду?
|
Номер сезона |
||
|
1-й спортсмен (Х) |
2-й спортсмен(Y) |
|
|
(время в мин.) |
(время в мин.) |
|
|
1 |
26,5 |
26,4 |
|
2 |
26,6 |
26,6 |
|
3 |
27 |
26,5 |
|
4 |
26 |
26,3 |
|
5 |
26,1 |
26,4 |
Подвести итог самостоятельной работы.
4. Итог урока.
Слайд 11 – выводы (комментарии учителя).
Слайд 12 – вопросы (ответы учеников).
Изучая математическую статистику в 7-м классе,
важно наглядно представить учащимися образец
для решения практических задач. Именно для этого
мною был разработан данный справочный материал.
1.Представление данных.
1.1. Таблицы
Смета расходов на покупку спортивного
инвентаря.
| № | Наименование | Ед. измерения | Количество | Цена (едруб) | Стоимость (руб) |
| 1 | Мяч футбольный | Шт. | 30 | 1000 |  |
| 2 | Мяч волейбольный | Шт. | 15 | 800 | 12000 |
| 3 | Ракетка | Шт. | 24 | 250 | 6000 |
| 4 | Воланы | коробка | 10 | 300 | 3000 |
| ИТОГО: | 51000 |
Таблицы предназначены для упорядочивания
большого количества данных. Часто в таблицы
заносят результаты вычислений, измерений.
1.2. Диаграммы.
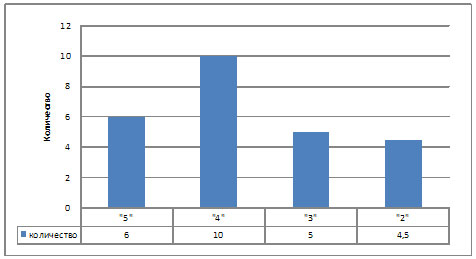
За контрольную работу по математике
школьники получили 6 оценок “отлично”, 10 оценок
“хорошо”, 5 оценок “ удовлетворительно” и 3
оценки “не удовлетворительно”.
Столбиковая диаграмма.
Построим столбиковую диаграмму по
этим данным.
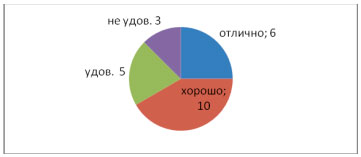
Круговая диаграмма.
Построим круговую диаграмму по этим
данным.
Для построения этой диаграммы мы:
- Разделили 360° на общее число учащихся (24)
- Затем последовательно умножаем 15° на
количество учащихся, получивших ту или иную
оценку. - Затем круг делим на полученные сектора,
подписываем данные.
360°24=15° (такому углу соответствует
оценка одного учащегося)
15°
6=90° —
сектор образованный этим углом соответствует
учащимся с оценкой “5”
15°10=150°
— сектор образованный этим углом соответствует
учащимся с оценкой “4”
15°5=75° —
сектор образованный этим углом соответствует
учащимся с оценкой “3”
15°3=45° —
сектор образованный этим углом соответствует
учащимся с оценкой “2”
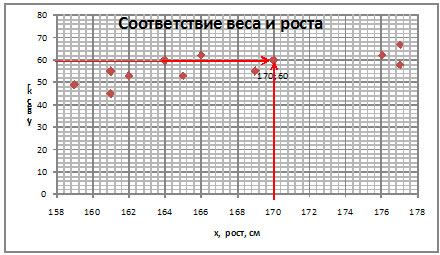
Диаграмма рассеивания.
Для выявления связи между величинами
применяются диаграммы рассеивания.
В таблице приведены данные о весе и
росте 12 девушек.
|
Рост, см |
165 |
177 |
161 |
162 |
170 |
176 |
177 |
164 |
166 |
161 |
169 |
159 |
Х |
|
Вес, кг |
53 |
67 |
45 |
53 |
60 |
62 |
58 |
60 |
62 |
55 |
55 |
49 |
У |
Для построения этой диаграммы нужно в
системе координат поставить точки, абсциссы
которых – рост, а ординаты – вес.
- Описательная статистика
2.1. Среднее значение
Определение: Средним арифметическим
нескольких чисел называется число, равное
отношение суммы этих чисел к их количеству.
Среднее арифметическое набора чисел х1,х2,х3,х4,х5
принято обозначать 
. Например, среднее арифметическое
пяти чисел запишется так:
Здесь в числителе дроби — сумма данных пяти
чисел, а в знаменателе – их количество – 5.
Найти среднюю оценку учащегося по
математике, если за истекший период он получил: 3,
4, 4, 5, 3, 2, 4, 3.
Запишем дробь и вычислим ее значение:
2.2. Медиана
Определение: Число, разделяющее набор
чисел на две части, равные по численности, так что
с одной стороны от этого числа все значения
больше медианы, а с другой – меньше.
Метод вычисления медианы: Чтобы найти
медиану набора чисел нужно:
- Записать числа в порядке возрастания.
- Если в полученном наборе нечетное количество
членов, то медианой служит число стоящее
посередине. - Если в полученном наборе четное количество
членов, то медианой набора – есть полусумма двух
чисел, расположенных посередине.
Найти медиану набора чисел: 9,3, 1, 5, 7.
Запишем числа в порядке возрастания.
1, 3, 5, 7, 9.
Здесь медиана набора число, стоящее
посередине – 5.
Найти медиану набора чисел: 9,3, 1, 5, 7,8
Запишем числа в порядке возрастания.
Выберем два центральных числа: 5 и 7. Найдем их
полусумму: (5+7):2=6. То есть медиана
данного набора есть число-6.
2.3. Наибольшее и наименьшее значение и размах.
Найти наибольшее, наименьшее значение и
размах для ряда чисел:
12,7,25,3,19,15.
Очевидно, что наибольшим значением данного
ряда является число 25, тогда как наименьшим число
– 3. Найдем размах данного ряда.
Определение: Разность между наибольшим и
наименьшим числом называется размахом набора
чисел.
Размах показывает насколько велико
рассеивание в числовом наборе. Итак, размах
данного набора равен разности 25 и 3, т.е. 22.
2.4. Отклонение.
Определение: Отклонением данного
значения от среднего арифметического значения
данного набора является разность между этим
числом и средним арифметическим. Соответственно
если некоторое значение меньше среднего, то его
отклонение отрицательно, если больше среднего –
его отклонение положительно. Так же необходимо
помнить, что сумма всех отклонений ряда чисел от
среднего арифметического этих чисел равна нулю.
Составить таблицу отклонений от
среднего арифметического для набора чисел:
2,4,5,7,10.
Вычислим среднее арифметическое этих чисел:
Составим таблицу отклонений.
| Число | Отклонение от среднего арифметического |
| 2 | 2-5,6= -3,6 |
| 4 | 4-5,6= -1,6 |
| 5 | 5-5,6= -0,6 |
| 7 | 7-5,6=1,4 |
| 10 | 10-5,6=4,4 |
2.5. Дисперсия.
Определение: Среднее арифметическое
квадратов отклонений от среднего значения
называется дисперсией набора чисел. Дисперсию
обозначают S2.
В таблице представлены средние
месячные температуры, в градусах. Вычислите
дисперсию температуры за приведенный период.
| Месяцы | Январь | Февраль | Март | Апрель | Май |
| Средняя температура | -12 | -7 | 0 | 9 | 16 |
Решение:
- Вычислим среднюю температуру за 5 месецев.
- .Составим таблицу отклонений и их квадратов.
- Найдем среднее арифметическое для квадратов
отклонений от среднего значения
Итак, средняя температура составила 6
градусов.
| Число (температура) | Отклонение от среднего | Квадрат отклонения |
| -12 | -12-6=-18 | (-18)2=324 |
| -7 | -13 | 169 |
| 0 | -6 | 36 |
| 9 | 3 | 9 |
| 16 | 10 | 100 |
( последний столбец таблицы)
Итак, дисперсия средних температур за 5 месяцев
составила 127,6. Ответ: S2=127,6
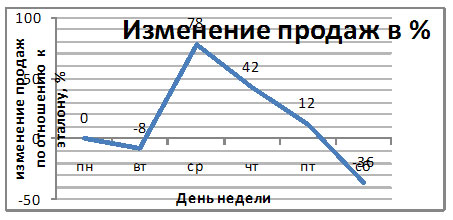
Составление таблицы изменений в процентах.
В таблице представлено количество
продаваемых за неделю шоколадок в школьном
буфете. Составьте таблицу изменения продаж по
отношению к понедельнику в процентах.
|
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
|
Количество |
50 |
46 |
89 |
71 |
44 |
32 |
Число проданных в понедельник шоколадок
составляет 100% — эталон.
Вычислим, сколько составляет 1% эталона.
1% =50:100=0,5.
Вычислим, сколько процентов эталона составляет
количество проданных шоколадок в другие дни
недели.
Вторник – 46. Какой процент составляет 46 от 50.
46:0,5=92
Среда -89. 89 : 0,5= 178
Четверг – 71. 71 :0,5=142
Пятница – 44 44:0,5=88
Суббота -32 32 :0,5 =64
|
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
|
Количество проданных |
50 |
46 |
89 |
71 |
44 |
32 |
|
% от эталона |
100 |
92 |
178 |
142 |
88 |
64 |
|
Изменение продаж в % |
0 |
-8 |
78 |
42 |
-12 |
-36 |
Скачать материал
Выберите документ из архива для просмотра:
Статистика.pptx
Выбранный для просмотра документ Статистика.pptx
Скачать материал
- Сейчас обучается 139 человек из 50 регионов
- Сейчас обучается 143 человека из 49 регионов
- Сейчас обучается 28 человек из 18 регионов
Описание презентации по отдельным слайдам:
-
1 слайд
Муниципальное казенное образовательное учреждение
«Малокрасноярская основная общеобразовательная школа»
Кыштовского района Новосибирской областиИзучение статистических характеристик в курсе школьной математики
Урок математики в 7 классе
Автор: Еланцева Светлана Викторовна,
учитель математики -
2 слайд
Среднее арифметическое
Определение: Средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.
-
3 слайд
Пример: Средняя оценка успеваемости за 1 четверть:
Среднее арифметическое:
(3 4 + 4 8 + 5 2):14 ≈3,85.
Получаем, что средняя оценка составляет приблизительно 3,85 -
4 слайд
Мода (Мо)
Модой называется то число, которое в данном числовом ряду встречается чаще всего. В числовом ряду может быть одна мода или несколько.
Например: Найти моду ряда чисел: 2,2,3,3,3,4,4,5,5,5,5,6,6,7. Чаще всего встречается число 5, значит Мо = 5.
-
5 слайд
Пример нахождения моды:
В отделе мужской обуви универмага в течение дня производился учет размеров купленной обуви.
Были получены следующие результаты: 42, 40, 43, 39, 42, 42, 45, 41, 43, 43, 41, 42, 46, 40, 42, 42, 39, 42, 45, 42, 43, 42, 44, 41, 42.
Какой размер обуви наиболее распространен, т.е. найти моду.
Чаще всего встречается 42 размер, значит Мо = 42 -
6 слайд
Наибольшее и наименьшее значение. Размах (А).
Определение: Разность между наибольшим и наименьшим числом называется размахом набора чисел.
Урожай картофеля в сёлах А и В:
Самый большой урожай в селе А:180ц/га, самый маленький — 50 ц/га.
В селе В: самый большой – 130 ц/га, самый маленький – 100 ц/га. Размах производства картофеля в селе А: 180 – 50 = 130,
в селе В: 130 – 100 = 30. -
7 слайд
Медиана (Ме)
Определение: Медианой набора чисел называют такое число, которое разделяет набор на две равные по численности части.
Прежде чем искать медиану ряда, нужно упорядочить ряд чисел.
-
8 слайд
Примеры нахождения медианы
Пример 1. Возьмём какой-нибудь набор различных чисел, например 1,4,7,9,11 — чётный ряд
Медианой в этом случае оказывается число, стоящее в точности посередине, m=7.Пример 2. Рассмотрим набор 1,3,6,11. – нечётный ряд Медианой этого набора служит число, равное полусумме чисел, стоящих посередине:
(3+6):2=4,5
Медианой этого набора считают число 4,5. -
9 слайд
Среднее геометрическое
Определение. Средним геометрическим нескольких чисел называется квадратный корень из произведения этих чисел.Например: Даны числа: 2; 5; 10.
Ср. геометрическое = 2*5*10 =10
-
10 слайд
Отклонения
Определение: отклонение – это разница между каждым числом набора и средним арифметическим ряда чисел.
Пример:
Возьмём набор чисел 1,6,7,9,12.
Вычислим среднее арифметическое: (1+6+7+9+12):5=7. Найдём отклонение каждого числа от среднего арифметического:
1-7=-6, 6-7=-1, 7-7=0, 9-7=2, 12-7=5.Сумма отклонений чисел от среднего арифметического этих чисел равна нулю.
-
11 слайд
Дисперсия
Определение: среднее арифметическое квадратов отклонений от среднего значения называется в статистике дисперсией набора чисел.
-
12 слайд
Производство картофеля ( ц/га)
Среднее арифметическое = 118,5 ц/га
Для расчета дисперсии следует сложить все значения в столбце «Квадрат отклонения» и разделить на количество слагаемых:(3721+4692,25+342,25+812,25+2,25+72,25+3782,25):7=1917,78.
-
13 слайд
Упражнения
1. Записан вес (в кг) семи учащихся:
42, 59, 48, 52, 61, 45, 64. Насколько среднее арифметическое этого набора чисел больше его медианы?
Решение. Упорядочим ряд чисел:
42,45,48, 52, 59, 61, 64.
Среднее арифметическое: (42+45+48+52+59+61+64):7=53
Медиана: 52
Разница: 53 — 52 = 1 -
14 слайд
Упражнения
2. Записан примерный пробег (в тыс.км) шести автомобилей: 70, 127, 70, 60, 53, 70. Насколько отличается мода этого набора чисел от его среднего арифметического?
Решение.
Среднее арифметическое ряда:
( 70 + 127 + 70 + 60 + 53 + 70) : 6 = 75
Мода: 70
Разница: 75 – 70 = 5 -
15 слайд
Упражнения
3. Даны числа: 18, 125, и 12. Найти разность между средним арифметическим и средним геометрическим этих чисел.
Решение.
Среднее арифметическое:
(18 + 125 + 12) : 3 = 51,6
Среднее геометрическое:
18 125 12 = 164,3
Разность: 164,3 – 51,6 = 112,7 -
16 слайд
Упражнения
4. Записан вес (в кг) шести учащихся:
55, 54, 61, 58, 55, 59. Насколько максимальное значение этого набора чисел отличается от его среднего арифметического?Решение: Максимальное значение = 61
Среднее арифметическое = (55+54+61+58+55+59) : 6 = 57
Разница: 61 – 57 = 4 -
17 слайд
Упражнения
5. В таблице приведены данные о пяти лучших результатах прыжков в длину с места учащихся старших классов:Определить дисперсию результатов прыжков, представленных в таблице. (Ответ округлить до сотых).
Решение. Среднее арифметическое:(183+185+180+186+185):5=183,8
Отклонения:(- 0,8; 1,2; — 3,8; 2,2; 1,2) (Проверка: Сумма = 0)
Квадрат отклонений: 0,64; 1,44; 14,44, 4,84; 1,44.
Дисперсия = (0,64 + 1,44 + 14,44 + 4,84 + 1,44) : 5 = 4,56. -
18 слайд
Упражнения
6. В таблице приведены данные книжного магазина о количестве проданных книг шести авторов в течение месяца:Определить, насколько отличается размах от медианы ряда количества проданных книг этих авторов.
Решение.
Упорядочим ряд: 30, 35, 38, 40, 42, 45. Размах = (45 – 30) = 15
Медиана = (38 + 40) : 2 = 36.
Разница: 36 – 15 = 21
Краткое описание документа:
Презентация «Изучение статистических характеристик по алгебре в 7 классе» окажет помощь учителю в изучении раздела «Статистические характеристики» по алгебре в 7 классе.
Материал презентации выходит за рамки учебника. Кроме тех характеристик, которые рассматриваются по программе:среднее арифметическое, размах, мода и медиана, в содержание презентации добавлены такие характеристики, как: среднее геометрическое, наибольшее и наименьшее значение, отклонение, дисперсия.
На каждую характеристику подобраны упражнения, которые будут полезны учащимся с высоким уровнем обучаемости при изучении высшей математики.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 263 391 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 16.11.2014
- 1158
- 2
Рейтинг:
5 из 5
- 16.11.2014
- 920
- 0
- 16.11.2014
- 2190
- 0
- 16.11.2014
- 865
- 0
- 16.11.2014
- 1122
- 1
- 16.11.2014
- 26432
- 100
- 16.11.2014
- 983
- 0