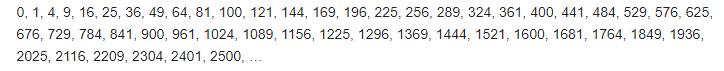Download Article
Download Article
Need to find the square of a number? Finding a number’s square is as simple as multiplying it by itself. To square fractions, find the squares of both the numerator and denominator. Then reduce or simplify the result. Keep reading for helpful tips and examples!
-
1
Learn how to do basic multiplication. When you square a number, you simply multiply the number by itself so it’s important to know how to multiply. To make it easier to square commonly used single digits, try to memorize basic times tables.[1]
- For example, learn how to multiply single digit times tables.
-
2
Multiply the single digit number by itself. Write down the number you want to square. Remember that when you’re squaring a number, you multiply it by the same number, not 2.[2]
- For example,
is not 5 x 2 = 10. Instead, it’s 5 x 5 = 25.
Advertisement
- For example,
-
3
Recognize other terms for squaring a number. If you read word problems asking you to square a number, keep in mind that they may also ask you to raise the number to the 2 power or factor. This is just another way of asking you to square the number.[3]
- You may also see a problem written as 6^2. This is another way of asking you to square 6.
-
4
Distinguish between squaring and finding the square root. It’s easy to get these terms mixed up, but remember that finding the square root of a number is the opposite of squaring a number. Finding the square root means that you’re looking for the number that can be multiplied by itself to get the number in the square.[4]
Advertisement
-
1
Write the problem out. To find the square of a number with more than 1 digit, it will help if you rewrite the problem as a double digit multiplication problem. Start by writing the same number on top of itself.[5]
- For example, to do
, write 24 x 24.
- For example, to do
-
2
Multiply the number on the bottom ones place by the 1 directly above it. Write a line below the numbers and place the result below the ones space.[6]
- For example, with 24 x 24, multiply the 4 by 4 to get 16. Write a 6 below the ones space and carry the 1 above the top tens number.
-
3
Multiply the bottom ones place by the top tens number. Take the same number on the bottom and multiply it by the top tens number. Remember to add the number you carried and write the result below the line.[7]
- For example, with 24 x 24, multiply 4 by 2 and add the 1 you carried. The result below the line should be 96.
-
4
Put a 0 under the result and multiply the bottom tens number by the top ones. The 0 will act as a placeholder. Write the result of multiplying the bottom tens number by the top ones number next to the 0.[8]
- For the 24 x 24 example, multiply 2 by 4. You should now see 80 below the 96.
-
5
Multiply the bottom tens number by the top tens number. If you carried any numbers, remember to add them to your result. Write the result below the line.[9]
- To finish multiplying 24 by 24, multiply the 2 by 2 to get 4. The result on this line should be 480.
-
6
Add the 2 results to get your answer. If you multiplied a number with 3 or more digits, you’ll have more lines to add together. Write the answer from your results to show the square of the number.
- Add 96 + 480 to get the answer for 24 x 24.
= 576.
- Add 96 + 480 to get the answer for 24 x 24.
Advertisement
-
1
Square the numerator. Multiply the top number of the fraction by itself to find its square. Write the result and place the fraction line below it.[10]
- For example, with (8/2)2, you’d multiply 8 by 8 to get a numerator of 64.
-
2
Square the denominator. Multiply the bottom number of the fraction by itself. Write the result of this square below the fraction line.[11]
- So for (8/2)2, multiply 2 by 2 to get a denominator of 4.
-
3
Simplify the result. While you could leave the fraction large or improper, most directions will tell you to simplify or reduce the result. If you have an improper fraction, turn it into a mixed number.[12]
- For example, (8/2)2 = (64/4) can be simplified to 16 because 4 goes into 64 16 times.
Advertisement
Add New Question
-
Question
How do I calculate the square root?
-
Question
√5 is the square of what number?
√5 is the square of plus-or-minus the fourth root of 5.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Remember that if you square a negative number, the answer will be positive because the 2 negatives cancel each other out.
-
To square a number using a calculator, enter the number x the number. For example, for
, enter 4 x 4 to get 16.
Advertisement
About This Article
Article SummaryX
To find the square of a number, multiply the number by itself. For example, if you’re trying to find the square of 5, you would multiply 5 by 5 and get 25, which is the square. To learn how to square fractions, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 120,875 times.
Did this article help you?
В этой статье мы поговорим, что такое квадрат числа, как его найти, а также каким образом производятся подобные вычисления в программировании.
Квадратом Х называют произведение 2-х множителей, каждый из которых равен Х.
Обозначение квадрата осуществляется с помощью степени, то есть Х² читается «Х в квадрате».
Если говорить еще более простым языком, то квадратом можно назвать число, которое умножено само на себя. Таким образом, мы можем написать простейшую формулу вычисления Х2:
Х2 = Х ⋅ Х
Почему вообще такое выражение называют квадратом X? Дело в том, что именно данной формулой выражают площадь квадрата, сторона которого равна X, то есть геометрически это значение можно представить в виде площади квадрата, имеющего целочисленную сторону.
Вывод тут прост: для решение поставленной задачи следует требуемое значение взять в качестве множителя дважды, а потом вычислить произведение. Соответственно:
32 = 3 ⋅ 3 = 9
52 = 5 ⋅ 5 = 25
102 = 10 ⋅ 10 = 100
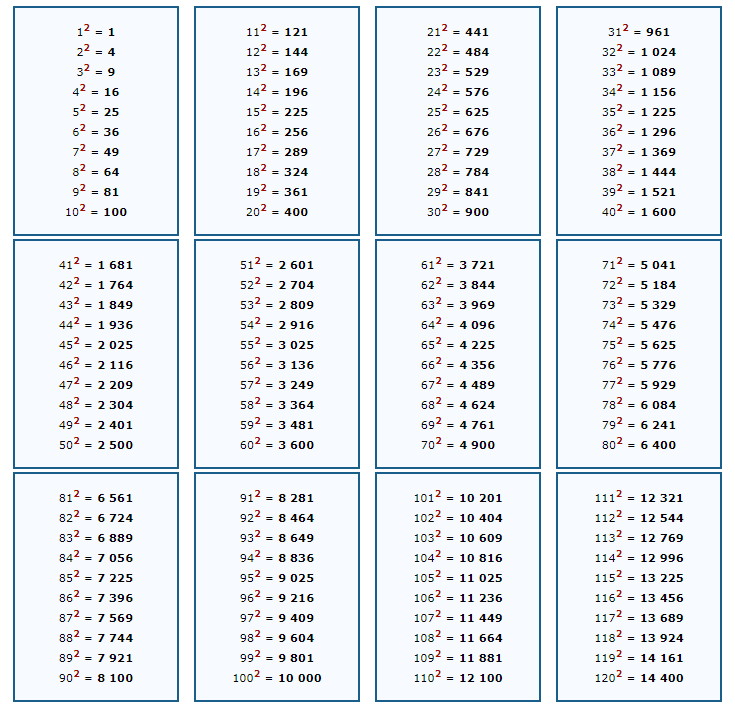
Это все элементарно и проходится в начальных классах средней школы. Решить такой пример в математике не проблема, а когда числовые значения выходят за рамки классической таблицы умножения, используют таблицу, ускоряющую расчеты.
Также описанную математическую операцию можно рассматривать в контексте частного случая возведения в степень — ведь именно этим, по сути, она и является — возведением в степень 2.
Интерес представляет и числовая последовательность для квадратов целых чисел, являющихся неотрицательными (речь идет о последовательности A000290 в OEIS):
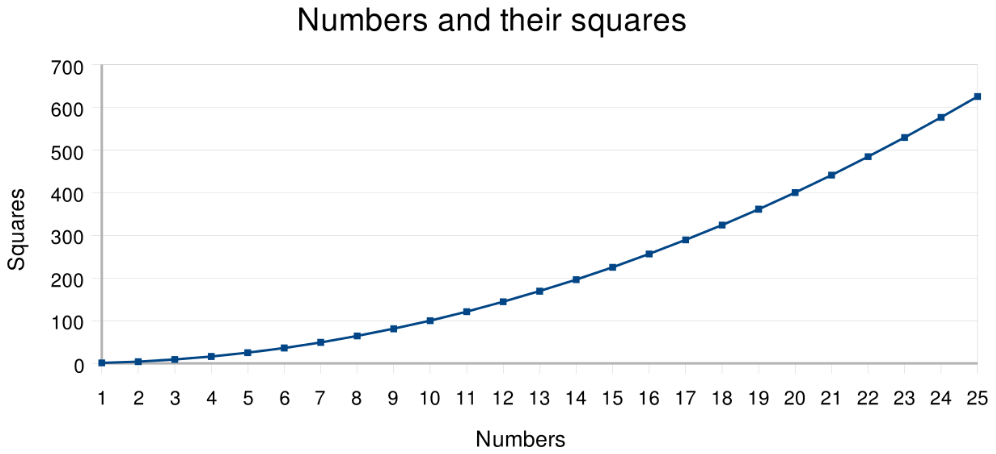
Нельзя не сказать и про график y=x², где представлены целые значения x на отрезке 1-25.
Квадратные числа
Если же говорить о натуральных числах из последовательности, упомянутой выше, в историческом контексте, то их всегда называли «квадратными». Квадратное числовое значение также называют полным либо точным квадратом, то есть целым значением, квадратный корень из которого можно извлечь нацело. К примеру, найти корень из 9 несложно (√9 = 3, т. к. 3 ⋅ 3 = 9). Не составляет проблем и вычислить корень из ста: (√100 = 10, ведь десять на десять равно сто).
Легко понять, что сто — это квадратное число, так как его можно записать в виде 10 ⋅ 10, плюс оно может быть представлено, как было сказано выше, в качестве площади квадрата со стороной, равной десяти. Таким образом, можно сделать вывод, что квадратное число включено в категорию классических фигурных чисел, то есть чисел, которые мы можем представить в виде геометрических фигур. Но в эту тему углубляться пока не будем.
А что в программировании?
Теперь давайте посмотрим, как все это работает в программировании. Для примера возьмем такой язык программирования, как Java (кстати, статья о том, как выполнять возведение в степень в Java, уже была).
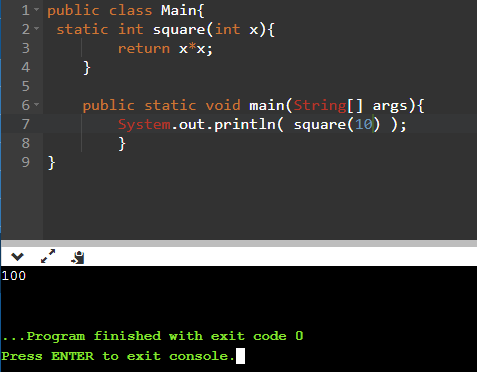
Напишем простой метод по возведению любых числовых значений в квадрат:
public class Main{
static int square(int x){
return x*x;
}
public static void main(String[] args){
System.out.println( square(10) );
}
}
Вы можете воспользоваться любым онлайн-компилятором для проверки этого кода. Также никто не мешает вписать любое число вместо десяти.
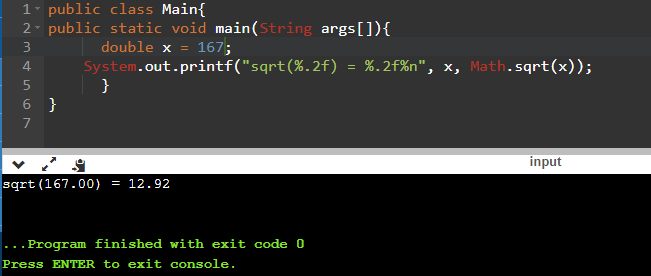
Теперь воспользуемся простейшей программой для того, чтобы найти квадратный корень из 100:
public class Main{
public static void main(String args[]){
double x = 100;
System.out.printf("sqrt(%.2f) = %.2f%n", x, Math.sqrt(x));
}
}
Программа позволяет извлекать корень и из неквадратных значений. Ниже мы находим корень из 167:
Да, в современную эпоху калькуляторов мало кто считает в уме. Вдобавок ко всему, сегодня даже не надо покупать настоящий калькулятор, так как калькулятор есть в любом мобильном телефоне, не говоря уже об онлайн-калькуляторах, коих существует огромное количество. Однако это не значит, что можно забыть азы алгебры. Не зря же великий русский ученый Михаил Ломоносов когда-то сказал:
По материалам:
- https://calculator888.ru/tablitsa-kvadratov;
- http://www.for6cl.uznateshe.ru/kvadrat-chisla/;
- https:/ru.wikipedia.org/.
Таблица квадратов натуральных чисел. Формулы сокращенного умножения
Как научиться считать быстро и без калькулятора? Ведь и на ЕГЭ, и на ОГЭ по математике пользоваться калькулятором вы не можете.
Первое, что вам поможет, — это знание таблицы квадратов натуральных чисел. Учите наизусть, как таблицу умножения!
Все мы изучали в средней школе формулы сокращенного умножения. Правда, тогда мы не вполне понимали, зачем нам это надо. Все эти квадраты суммы и разности квадратов… А нужны они для того, чтобы быстро считать. И когда на ЕГЭ по математике на решение варианта у вас всего 3 часа 55 минут, а успеть надо очень много, — эти формулы просто незаменимы.
Как применять эти формулы на практике?
Например,
;
.
И более сложная ситуация. Она может вам встретиться в задании 7 Профильного ЕГЭ по математике, если вдруг придется считать площадь криволинейной под графиком функции как разность первообразных.
Правда, есть и более простое решение этой задачи. И в нем тоже используется одна из формул сокращенного умножения.
А вот и еще один полезный лайфхак:
Числа, оканчивающиеся на 5, в квадрат возводятся мгновенно.
Чтобы найти квадрат числа (
– не обязательно цифра, любое натуральное число), умножаем
на
и к результату приписываем 25.)
Например,
.
Разберем еще несколько примеров на формулы сокращенного умножения.
1. Вычислите:
Решение:
Применим формулу разности кубов для выражения в числителе.
Ответ: 123.
2. Вычислите
Решение:
Конечно, мы не будем отдельно вычислять значения выражений в числителе и знаменателе дроби.
Применим формулы сокращенного умножения. В числителе – квадрат разности. В знаменателе – разность квадратов.
Ответ: 1,25.
Такие задания могут встретиться в первой части ЕГЭ по математике. А вычисления этого типа – в «экономической» задаче из второй части.
3. Найдите значение выражения если a = 47, b = 999.
Решение:
Числитель дроби является полным квадратом;
Знаменатель дроби преобразуем к виду:
Получим:
Если a = 47, b = 999, получаем:
4. Найдите значение выражения:
Решение:
Сделаем замену переменной: тогда
Запишем выражение в виде:
Квадратный трехчлен имеет корни
и
поэтому
Ответ: 2.
Рассмотрим задачи по теме: разложение на множители. Здесь мы тоже применяем формулы сокращенного умножения: разность квадратов, квадрат суммы и квадрат разности, разность кубов, сумма кубов… Все это может пригодиться, например, при решении задач с параметрами, а также уравнений и неравенств на ЕГЭ по математике.
Разложите на множители:
5.
Решение:
Применим формулу разности квадратов.
6.
Каждое из слагаемых содержит m в целой степени. Вынесем за скобки Также за скобки можно вынести 12. Получим:
Здесь мы применили формулу квадрата суммы.
7.
Решение:
Представим выражение в виде:
Выражение в скобках – это квадрат суммы. Получим:
Это разность квадратов. Применяем формулу:
разложили на множители.
8.
Такое выражение может встретиться в задаче с параметрами. Разложим его на множители:
9.
Решение:
Первые три слагаемые образуют полный квадрат:
Следовательно,
10.
Решение. Последние три слагаемые после вынесения знака минус образуют полный квадрат:
Тогда
Воспользуемся формулой разности квадратов и получим:
Тогда
Ответ:
Формулы сокращенного умножения помогут также при решении уравнений.
11. Решите уравнение:
Решение: По формуле разности кубов,
Тогда
Подставив в наше уравнение, получим:
Ответ: 2
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Таблица квадратов натуральных чисел. Формулы сокращенного умножения» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Таблица квадратов
Скачать таблицу квадратов
Определение. Квадрат числа — есть данное число, возведенное во вторую степень (число умноженное само на себя).
a2 = a · a
«Квадратом» оно называется, потому что такая операция аналогична вычислению площади квадрата.
Калькулятор для вычисления квадрата числа
2 = 49 ≈ 0.4444444444444444
Ниже приведены две удобные таблицы квадратов натуральных чисел от 1 до 100.
Таблица квадратов чисел от 1 до 100
|
12 = 1 22 = 4 32 = 9 42 = 16 52 = 25 62 = 36 72 = 49 82 = 64 92 = 81 102 = 100 |
112 = 121 122 = 144 132 = 169 142 = 196 152 = 225 162 = 256 172 = 289 182 = 324 192 = 361 202 = 400 |
212 = 441 222 = 484 232 = 529 242 = 576 252 = 625 262 = 676 272 = 729 282 = 784 292 = 841 302 = 900 |
312 = 961 322 = 1024 332 = 1089 342 = 1156 352 = 1225 362 = 1296 372 = 1369 382 = 1444 392 = 1521 402 = 1600 |
412 = 1681 422 = 1764 432 = 1849 442 = 1936 452 = 2025 462 = 2116 472 = 2209 482 = 2304 492 = 2401 502 = 2500 |
|
512 = 2601 522 = 2704 532 = 2809 542 = 2916 552 = 3025 562 = 3136 572 = 3249 582 = 3364 592 = 3481 602 = 3600 |
612 = 3721 622 = 3844 632 = 3969 642 = 4096 652 = 4225 662 = 4356 672 = 4489 682 = 4624 692 = 4761 702 = 4900 |
712 = 5041 722 = 5184 732 = 5329 742 = 5476 752 = 5625 762 = 5776 772 = 5929 782 = 6084 792 = 6241 802 = 6400 |
812 = 6561 822 = 6724 832 = 6889 842 = 7056 852 = 7225 862 = 7396 872 = 7569 882 = 7744 892 = 7921 902 = 8100 |
912 = 8281 922 = 8464 932 = 8649 942 = 8836 952 = 9025 962 = 9216 972 = 9409 982 = 9604 992 = 9801 1002 = 10000 |
Распечатать таблицу квадратов
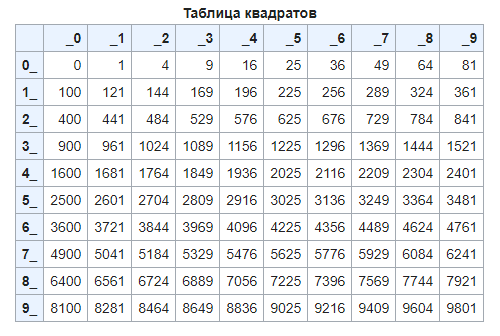
Таблица квадратов
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Распечатать таблицу квадратов
Что такое квадрат числа? Как найти квадрат числа?
Определение.
Квадрат числа a — это произведение двух множителей, каждый из которых равен a.
Квадрат числа a обозначают a². Читают: «a в квадрате».
С помощью формулы определение квадрата числа a можно записать так:
Выражение a² назвали квадратом числа a, так как именно такой формулой выражается площадь квадрата со стороной a.
Таким образом, чтобы найти квадрат некоторого числа, надо это число взять множителем два раза и вычислить произведение.
Например,
Если числовое выражение содержит квадрат числа, значение квадрата вычисляют до выполнения остальных действий.
Например,
В математике находить квадраты чисел приходится достаточно часто. Для ускорения вычислений используется таблица квадратов.