Как найти диагональ осевого сечения цилиндра
Цилиндр представляет собой тело, ограниченное цилиндрического поверхностью с основаниями в форме круга. Эта фигура образуется путем вращения прямоугольника вокруг своей оси. Осевое сечение — есть сечение, проходящее через цилиндрическую ось, оно представляет собой прямоугольник со сторонами, равными высоте цилиндра и диаметру его основания.

Инструкция
Условия задачи при нахождении диагонали осевого сечения цилиндра могут быть разными. Внимательно ознакомьтесь с текстом задачи, отметьте известные данные.
Радиус основания и высота цилиндраЕсли в вашей задаче известны такие показатели, как радиус цилиндра и его высота, то исходя из этого, найдите диагональ. Поскольку осевое сечение является прямоугольником со сторонами, которые равны высоте цилиндра и диаметру основания, то диагональ сечения — есть гипотенуза прямоугольных треугольников, образующих осевое сечение. Катетами в данном случае выступают радиус основания и высота цилиндра. По теореме Пифагора (c2 = a2 + b2) найдите диагональ осевого сечения:D = √〖(4R〗^2+H^2), где D – диагональ осевого сечения цилиндра, R – радиус основания, H – высота цилиндра.
Диаметр основания и высота цилиндраЕсли в задаче диаметр и высота цилиндра равны, то перед вами осевое сечение в форме квадрата, единственное отличие этого условия от предыдущего в том, что потребуется разделить на 2 диаметр основания. Далее действуйте в соответствии с теоремой Пифагора, как и при решении предыдущей задачи.
Высота и площадь полной поверхности цилиндраПрочитайте внимательно условия задачи, при известной высоте и площади обязательно должны быть даны скрытые данные, например, оговорка, что высота больше радиуса основания на 8 см. В таком случае найдите радиус из указанной площади, затем с помощью радиуса вычислите высоту, далее по теореме Пифагора – диаметр осевого сечения:Sp = 2πRH+2πR^2 , где Sp – площадь полной поверхности цилиндра.Отсюда выведите формулу нахождения высоты через площадь полной поверхности цилиндра, помните, что при данном условии H = 8R.H = (Sp — 2πR^2) / 2πR.
Полезный совет
Изображая чертеж на бумаге, старайтесь использовать как можно больше площади листа для изображения цилиндра. Чем выразительнее и крупнее чертеж, тем будет представляться решение задачи.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Диагональ цилиндра соединяет противоположные точки диаметров окружностей, служащих основаниями. Для того чтобы найти диагональ цилиндра, необходимо начертить диаметр нижнего основания из вершины диагонали и высоту цилиндра из верхней вершины диагонали. Эти отрезки в совокупности дают прямоугольный треугольник во внутреннем пространстве цилиндра, из которого по теореме Пифагора можно найти диагональ цилиндра. Катетами треугольника будут высота h и диаметр D, а диагональ цилиндра d будет гипотенузой.
Если известен радиус окружностей r, то можно подставить в формулу вместо диаметра удвоенный радиус:
Примечание. Это урок с решениями задач по геометрии (раздел цилиндр). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».
Задача
Осевое сечение цилиндра — квадрат, диагональ которого равна 4√2.
Вычислить объем цилиндра.
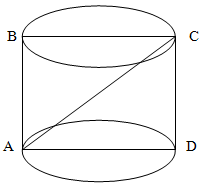
Решение.
Поскольку диагональ сечения цилиндра — квадрат, то обозначим его сторону как a.
a2 + a2 = (4√2)2
2a2 = 32
a2 = 16
a = 4
Объем цилиндра найдем по формуле:
V = πd2 / 4 * h
откуда
V = π42 / 4 * 4
V = 16π
Ответ: Объем цилиндра равен 16π
Задача
Куб с ребром длиной а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.
Решение.
Проведем плоскость через основание цилиндра.

Диагональ куба является одновременно диаметром цилиндра. Зная сторону куба, определяем длину диагонали AC квадрата ABCD как
CD2 + AD2= AC2
a2 + a2 = AC2
2a2 = AC
AC = a√2
Проведем плоскость через ось цилиндра по диагонали AC. Высота сечения равна длине ребра куба и по условиям задачи рана а, а ширина сечения равна a√2.
Таким образом, площадь сечения равна:
S = a * a√2 = a2√2
Ответ: a2√2
Задача
Диагональ осевого сечения цилиндра равна 12 см и образует с плоскостью нижнего основания угол 45 градусов. Найти обьём цилиндра.
Решение.
Поскольку основание осевого сечения образует с высотой цилиндра, принадлежащей сечению, прямой угол, то треугольник, который образован диагональю осевого сечения, высотой цилиндра и его диаметром — прямоугольный.
Исходя из этого, угол между диагональю и высотой также равен 45 градусов ( 180 — 90 — 45 ).
Таким образом, треугольник является равнобедренным, а, следовательно, высота цилиндра равна его диаметру. Применив теорему Пифагора, найдем их.
d2 + d2 = 122
2d2 = 144
d2 = 72
Теперь применим формулу объема цилиндра V = пd2 / 4 h
V = 72п / 4 * √72
V = 18п * √72
Ответ: 18п√72
Задача
|
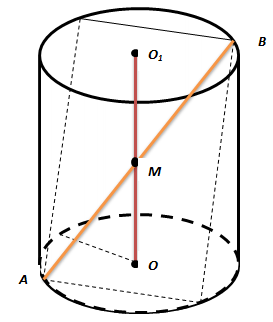
Высота цилиндра 2м. Радиус основания 7м. В этот цилиндр наклонно вписан квадрат так, что все вершины его лежат на окружностях оснований. Найти сторону квадрата. |
Висота циліндра 2м. Радіус основи 7м. В цей циліндр похило вписаний квадрат так, що всі вершини його лежать на окружностях основ. Знайти сторону квадрата. |
Решение. Рiшення.
|
В силу симметричности квадрата и цилиндра и ввиду того, что квадрат наклонный, диагональ квадрата пересечет ось цилиндра ОО1 в точке М, являющейся серединой отрезкаОО1. По условию ОО1=2м, а ОА=7 м, поэтому ОМ=1м.
Пусть d – диагональ квадрата. Тогда сторона квадрата а равна: |
У силу симетричності квадрата і циліндра і зважаючи на те, що квадрат похилий, діагональ квадрата перетне вісь циліндра ОО1 в точці М, яка є серединою відрізка ОО1. За умовою ОО1=2м, а ОА=7 м, тому ОМ=1м.
Позначимо d – діагональ квадрата. Тоді сторона квадрата а: |
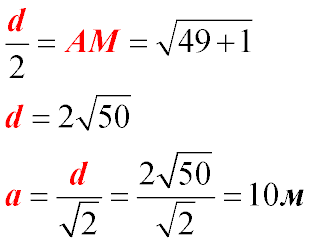
0
Цилиндр и его сечения |
Описание курса
| Диагональ цилиндра


