Как найти квадрат числа тема - Avtoru.top - решение различных проблем

Download Article

Need to find the square of a number? Finding a number’s square is as simple as multiplying it by itself. To square fractions, find the squares of both the numerator and denominator. Then reduce or simplify the result. Keep reading for helpful tips and examples!

1
Learn how to do basic multiplication. When you square a number, you simply multiply the number by itself so it’s important to know how to multiply. To make it easier to square commonly used single digits, try to memorize basic times tables.^[1]
- For example, learn how to multiply single digit times tables.
2
Multiply the single digit number by itself. Write down the number you want to square. Remember that when you’re squaring a number, you multiply it by the same number, not 2.^[2]
- For example, $5^{{2}}$ is not 5 x 2 = 10. Instead, it’s 5 x 5 = 25.
Advertisement
3
Recognize other terms for squaring a number. If you read word problems asking you to square a number, keep in mind that they may also ask you to raise the number to the 2 power or factor. This is just another way of asking you to square the number.^[3]
- You may also see a problem written as 6^2. This is another way of asking you to square 6.
4

Distinguish between squaring and finding the square root. It’s easy to get these terms mixed up, but remember that finding the square root of a number is the opposite of squaring a number. Finding the square root means that you’re looking for the number that can be multiplied by itself to get the number in the square.^[4]

1
Write the problem out. To find the square of a number with more than 1 digit, it will help if you rewrite the problem as a double digit multiplication problem. Start by writing the same number on top of itself.^[5]
- For example, to do $24^{{2}}$ , write 24 x 24.
2
Multiply the number on the bottom ones place by the 1 directly above it. Write a line below the numbers and place the result below the ones space.^[6]
- For example, with 24 x 24, multiply the 4 by 4 to get 16. Write a 6 below the ones space and carry the 1 above the top tens number.
3
Multiply the bottom ones place by the top tens number. Take the same number on the bottom and multiply it by the top tens number. Remember to add the number you carried and write the result below the line.^[7]
- For example, with 24 x 24, multiply 4 by 2 and add the 1 you carried. The result below the line should be 96.
4
Put a 0 under the result and multiply the bottom tens number by the top ones. The 0 will act as a placeholder. Write the result of multiplying the bottom tens number by the top ones number next to the 0.^[8]
- For the 24 x 24 example, multiply 2 by 4. You should now see 80 below the 96.
5
Multiply the bottom tens number by the top tens number. If you carried any numbers, remember to add them to your result. Write the result below the line.^[9]
- To finish multiplying 24 by 24, multiply the 2 by 2 to get 4. The result on this line should be 480.
6
Add the 2 results to get your answer. If you multiplied a number with 3 or more digits, you’ll have more lines to add together. Write the answer from your results to show the square of the number.
- Add 96 + 480 to get the answer for 24 x 24. $24^{{2}}$ = 576.

1
Square the numerator. Multiply the top number of the fraction by itself to find its square. Write the result and place the fraction line below it.^[10]
- For example, with (⁸/₂)², you’d multiply 8 by 8 to get a numerator of 64.
2
Square the denominator. Multiply the bottom number of the fraction by itself. Write the result of this square below the fraction line.^[11]
- So for (⁸/₂)², multiply 2 by 2 to get a denominator of 4.
3
Simplify the result. While you could leave the fraction large or improper, most directions will tell you to simplify or reduce the result. If you have an improper fraction, turn it into a mixed number.^[12]
- For example, (⁸/₂)² = (⁶⁴/₄) can be simplified to 16 because 4 goes into 64 16 times.

Add New Question

Question

How do I calculate the square root?
Question

√5 is the square of what number?

√5 is the square of plus-or-minus the fourth root of 5.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Remember that if you square a negative number, the answer will be positive because the 2 negatives cancel each other out.
To square a number using a calculator, enter the number x the number. For example, for $4^{{2}}$ , enter 4 x 4 to get 16.

About This Article

Article SummaryX

To find the square of a number, multiply the number by itself. For example, if you’re trying to find the square of 5, you would multiply 5 by 5 and get 25, which is the square. To learn how to square fractions, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 120,674 times.

Did this article help you?

Источник

Что такое квадрат числа? Как найти квадрат числа?

Определение.

Квадрат числа a — это произведение двух множителей, каждый из которых равен a.

Квадрат числа a обозначают a². Читают: «a в квадрате».

С помощью формулы определение квадрата числа a можно записать так:

$[{a^2} = a cdot a]$

Выражение a² назвали квадратом числа a, так как именно такой формулой выражается площадь квадрата со стороной a.

Таким образом, чтобы найти квадрат некоторого числа, надо это число взять множителем два раза и вычислить произведение.

Например,

$[{0^2} = 0 cdot 0 = 0;]$

$[{1^2} = 1 cdot 1 = 1;]$

$[{7^2} = 7 cdot 7 = 49;]$

$[{10^2} = 10 cdot 10 = 100;]$

$[{12^2} = 12 cdot 12 = 144.]$

Если числовое выражение содержит квадрат числа, значение квадрата вычисляют до выполнения остальных действий.

Например,

$[{9^2} + 2 cdot {(2 + 8)^2} = 81 + 2 cdot {10^2} = ]$

В математике находить квадраты чисел приходится достаточно часто. Для ускорения вычислений используется таблица квадратов.

Источник

Как найти квадрат числа

Учитель на уроке диктует математическое выражение для того, чтобы учащиеся записали его в тетрадь: «Три в квадрате минус пять…» Один ученик не успевая, просит: «Подождите, не говорите слишком быстро, я еще квадрат не нарисовал». Так вот, дабы не рисовать квадраты и кубы на математике, нужно знать, что квадратом числа является его вторая степень, то есть когда число умножается на себя два раза. Вычислять квадраты учат в еще школе: дважды два – четыре, пятью пять – двадцать пять.

Вам понадобится

— таблицы умножения;
— таблица квадратов двузначных чисел;
— калькулятор.

Инструкция

Чтобы найти квадрат любого числа достаточно только это число умножить на себя. Пример 1. 6*6 =36; 4*4 = 16; 7*7 = 49. Произведение чисел до 10, состоящих из одной цифры, размещено в таблице, знакомой всем еще с начальной школы: таблицы умножения. В ней по диагонали можно увидеть квадраты чисел: 1*1=1, 2*2=4, 3*3=9,4*4=16,5*5=25,6*6=36,7*7=49,8*8=64,9*9=81.

Вторая степень двузначных чисел (например, числа 16, 79, 54) определяется тем же способом: умножением числа на себя. Пример2. 20*20=400; 25*25=625; 40*40=1600. Существует специальная таблица квадратов двузначных чисел, размещенная в учебнике по алгебре для седьмого класса. В ней легко найти квадрат любого числа. Для этого разбейте число, возводимое в квадрат на десятки и единицы. Найдите пересечение строки-десятков и столбца-единиц по указанной таблице — ячейка на пересечении и будет содержать квадрат данного числа.

Если под рукой нет таблицы, квадрат числа можно найти произведением числа на само себя, выполненное в столбик. Этим способом находится и квадрат числа, состоящего из любого количества цифр. Однако квадрат большого числа лучше вычислить с помощью калькулятора. Для этого умножьте на нем заданное число само на себя. Сначала наберите нужное число с помощью цифровой клавиатуры, затем нажмите кнопку «*». После этого еще раз наберите это же число и в заключении кнопку «=». Калькулятор представит на экране точный ответ квадрата числа.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Урок по математике 5 класс, составила
учитель математики Шмыгина Т.Н.

Тема урока: « Квадрат числа».

Цели:

1)
Познавательный аспект цели:

— обеспечить усвоение
понятия: квадрат числа, нахождения значения выражения с квадратом числа на
уровне воспроизведения по образцу, творческого применения;

— формировать умения
пользоваться карточками при самостоятельной работе;

— развивать умения устного
счета;

— продолжить формирование
обще учебных умений:

1. умений планировать
свою деятельность при выполнении всех самостоятельных работ;

2. умение контролировать
ход своей деятельности при проверке данных заданий по теме;

2) Развивающий аспект
цели:

— продолжить работу по развитию внимания
и мышления;

— умение обобщать при выполнении заданий на
этапах усвоения новых знаний, когда учащиеся делают вывод;

— умения продолжить аналогии при
составлении таблицы квадратов;

— продолжить работу над развитием речи при
устных ответах;

— развивать память, наблюдательность,
творческие способности, познавательные интересы;

— организовать смену видов сферы
деятельности.

3) Воспитательный аспект цели:

— продолжить формирование нравственных
отношений в процессе совместной деятельности (учитель – ученик, ученик —
учитель);

— продолжить работу над формированием
сознательной дисциплины;

-воспитывать аккуратность, добросовестное
отношение к работе, уважительное отношение к товарищам.

Тип урока: урок усвоения новых знаний и первичного осмысления.

Структура урока.

1.
Организация начала урока.

2.
Актуализация опорных знаний.

3.
Изучения нового материала и первичная
проверка усвоения знаний, самоконтроль.

4.
Закрепления новых знаний.

5.
Подведение итогов.

6.
Информация о домашнем задании.

Этап урока

Планируемая деятельность учителя

Деятельность ученика

1.
Организация начала урока (1 мин)

Здравствуйте ребята, садитесь. Сегодня на
уроке мы изучим новую тему, которую сейчас расшифруем. Для этого посчитаем
устно

2.
Актуализация опорных знаний (7 мин)

210 340 480 92

:7 +80 :60 -85

-10 :14 +15 х70

+5 х5 х3 +50

Х4 -70 -47 :60

А К Ч И

40 100 98 100

-71 -54 -59 -13

Х3 :23 :3 :3

+23 х19 +17 +27

:16 +22 х4 :14

В С Д Т

42 70

+26 -19

:2 :3

-16 +13

Х3 х5

Р Л

Итак, тема урока: «Квадрат числа». Сегодня
на уроке познакомимся с нахождением квадрата числа. Прежде чем приступать к
изучению нового материала устно выполним следующие задания.

1. Угадайте корни уравнения.

Что называют корнем
уравнения?

Найдите его.

х∙х=25; а∙а=1; b∙b∙b=0

2. Найдите площадь квадрата со стороной 8см.

Что такое квадрат?

Как найти площадь квадрата?

Найдите её.

Дети записывают тему урока в тетрадь

Учащиеся отвечают на вопросы

3.
Мотивация(2 мин)

Ребята, ко мне за помощью обратился ученик 9
класса, решите пример.

Давайте поможем ему. Чтобы решить данный
пример нужно изучить тему квадрат числа и знать правило выполнения действия,
если в выражение входит квадрат числа.

4.
Изучение нового материала(15 мин)

Для этого у вас на парте лежат карточки 3
уровней: на «5»,на «4»,и на «3». Выберите по какой карточке вы будете изучать
самостоятельно новый материал. Запишите фамилию, имя на карточке и
приступайте к работе, заполните карточку до таблицы квадратов. Кто справится
с заданиями 1…,2,3 поднимаем руку для проверки карточки.

Итак, квадратом числа m называют произведение m и m.
Обозначают

А сейчас заполним таблицу квадратов

m	1	2	3	4	5	6	7	8	9	10
	1	4	9	16	25	36	49	64	81	100

1²=1 2²=4 3²=9
4²=16 и т.д.

Игра. 1) квадрат какого числа равен 36.

2) Вычислите 3²

3) Квадрат какого числа равен 81 и т.д.

Учащиеся работают самостоятельно по
карточкам 3 уровней.

Записывают в тетрадь.

Физминутка (3 мин)

Следующее задание. Работаем по вариантам. Найдите
значение выражения !в. 2²+3²

2в. (2+3)²

Проверяем вывод: Если в числовое
выражение входит квадрат числа, то их значения вычисляется до выполнения
действия.

Если в выражение входит квадрат выражения,
то сначала действия в скобках, а затем квадрат полученного числа.

Вернемся к предложенному примеру и решим
его.

Учащиеся самостоятельно решают задания и
делают вывод

Закрепление знаний (5 мин)

А теперь проверим как вы усвоили данную тему
урока.

Предлагаю самостоятельную работу. Выберите
карточку по уровням. Несколько карточек возьму на проверку. Проверка на
доске.

Учащиеся самостоятельно выполняют задания

Итог урока (2 мин)

Что нового изучили?

Что называется квадратом числа а?

Как обозначают?

На следующем уроке после изучения куба
числа. Мы должны будем найти сходство и различия квадрата и куба числа. За
урок получили оценки….

Учащиеся отвечают на вопросы

Домашнее задание(2 мин)

П.16 № 666, 668(а,в,г),670 по действиям. На
«5» стр 141 Андрей Николаевич Колмагоров предлагает другой способ нахождения
квадрата числа, разберитесь с ним. И сравните какой из способов легче.

Учащиеся записывают домашнее задание в
дневник

Карточка на отметку «5» Ф.И._______________________________

Задание №1.

Найдите площадь квадрата со стороной 17см

17
S=______________см²

17
Ответ: S=________см²

Задание №2.

Выражение 17²
(читается 17 в квадрате)

Догадайся, как
найти значение выражения 17², если 17²=289

17²=____________=289

Сделай вывод,
запиши его____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Задание №3.

Вычислить
самостоятельно, работая в карточке

15²=_____________
63²=_____________ 0²=____________ с²=___________

Задание №4.

Сформулируйте
правило нахождения квадрата числа n_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Таблица
квадратов

N	1	2	3	4	5	6	7	8	9	10
N²

Карточка на отметку «5».

Выполните
решение задания в тетради.

Задание №5.

Найдите значение
выражения: (140 — 9²)(10 — 3)².

Задание №6.

Составьте
задачу, решением которой является выражение и реши её

(24-10)².

Карточка на
отметку «4».

Выполните
решение задания в тетради.

Задание №5.

Найдите значение
выражения: (4² +7)².

Задание №6.

Пользуясь
таблицей квадратов, найдите значение а , если а²=36; а²=1.

Карточка на
отметку «3».

Выполните
решение задания в тетради.

Задание №5.

Найдите значение
выражения: а) 5²+ 4 б) (1+5)².

Задание №6.

Пользуясь
таблицей квадратов, найдите значение n , если n
∙n =1

Карточка на
отметку «4». Ф.И.________________________________________________

Задание №1.

Найдите значение
выражения 81² (читается 81 в квадрате).

Решение.

Для
того чтобы найти 81²

1)
Найди произведение чисел 81· 81=_____________

2)
Решение запиши в виде 81²=81·81 =6561.

Сделай вывод. Допиши предложение. Чтобы
найти квадрат числа нужно найти произведение___________________________________________________________________________________

Задание №2.

Вычисли самостоятельно, работая в карточке

18²=________________________

22²=_________________________

1²= ______________________

N²=________________________

Задание №3.

Продолжи
правило:

Квадратом числа n называют произведение_________________________________________________________________________________________________________________________________________________________________________________

Запиши правило с помощью букв n²=____________________

n	1	2	3	4	5	6	7	8	9	10
N²

Карточка на
отметку «3». Ф.И._________________________________

Задание №1.

Найдите значение
выражения 11² (читается 11 в квадрате).

Решение.

Для того, чтобы
найти значение выражения 11²:

1)
Запиши 11² как произведение чисел
11·11=_________________________________________

2)
Выполни вычисление в столбик х11

_11_

3)
Проверь себя, решение записывается так 11²=11·11 =121.

4)
Значит, чтобы найти квадрат числа нужно
найти произведение двух множителей, каждый из которых равен этому числу.

Задание №2.

Найдите
значение выражения самостоятельно, работая в карточке.

5²= 5·5=___________

7²=7·7=___________

9²=9·_=_____________

Проверь себя: 5²=25, 7²=49, 9²=81.

Задание №3.

Прочитай правило: Произведение n
и n называют квадратом числа n
и обозначают n²

N²
= n·n

Пользуясь правилом, продолжи предложение:
«Квадратом числа а называют…………..»

______________________________________________________________________________________________________________________________________________________________________________________________Обозначают: ______________

А²=_____·_________

Таблица квадратов

n	1	2	3	4	5	6	7	8	9	10
N²

Источник

Быстрое возведение чисел от 1 до 100 в квадрат

Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.

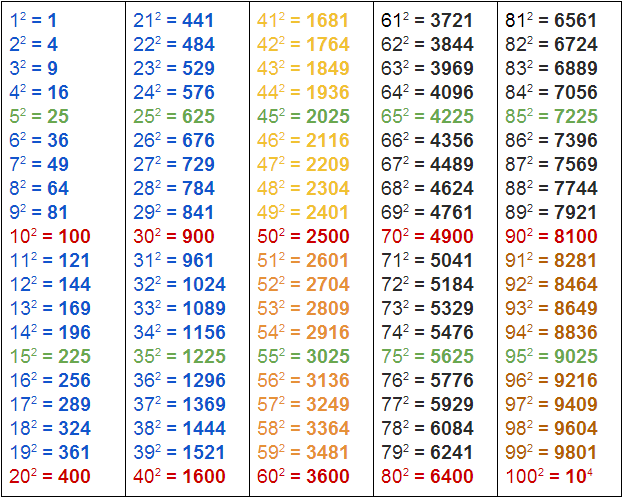
*квадраты до сотни

Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.

Правило 1 (отсекает 10 чисел)

Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.

В таблице отмечены красным.

Правило 2 (отсекает 10 чисел)

Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.

В таблице отмечены зеленым.

Правило 3 (отсекает 8 чисел)

Для чисел от 40 до 50.

Достаточно трудно, верно? Давайте разберем пример:

В таблице отмечены светло-оранжевым.

Правило 4 (отсекает 8 чисел)

Для чисел от 50 до 60.

Тоже достаточно трудно для восприятия. Давайте разберем пример:

В таблице отмечены темно-оранжевым.

Правило 5 (отсекает 8 чисел)

Для чисел от 90 до 100.

Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:

В таблице отмечены темно-темно-оранжевым.

Правило №6 (отсекает 32 числа)

Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 🙂
В таблице отмечены синим.

Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:

Формулы (осталось 24 числа)

Для чисел от 25 до 50

Для чисел от 50 до 100

Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):

UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»:

Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».

Для квадратов, соответственно, еще проще.

Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.

Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.

Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.

Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.

Таблица квадратов натуральных чисел. Формулы сокращенного умножения

Как научиться считать быстро и без калькулятора? Ведь и на ЕГЭ, и на ОГЭ по математике пользоваться калькулятором вы не можете.

Первое, что вам поможет, — это знание таблицы квадратов натуральных чисел. Учите наизусть, как таблицу умножения!

Все мы изучали в средней школе формулы сокращенного умножения. Правда, тогда мы не вполне понимали, зачем нам это надо. Все эти квадраты суммы и разности квадратов… А нужны они для того, чтобы быстро считать. И когда на ЕГЭ по математике на решение варианта у вас всего 3 часа 55 минут, а успеть надо очень много, — эти формулы просто незаменимы.

Как применять эти формулы на практике?

.
И более сложная ситуация. Она может вам встретиться в задании 7 Профильного ЕГЭ по математике, если вдруг придется считать площадь криволинейной под графиком функции как разность первообразных.

Правда, есть и более простое решение этой задачи. И в нем тоже используется одна из формул сокращенного умножения.

А вот и еще один полезный лайфхак:

Числа, оканчивающиеся на 5, в квадрат возводятся мгновенно.

Чтобы найти квадрат числа ( – не обязательно цифра, любое натуральное число), умножаем на и к результату приписываем 25.)

Таблица квадратов от 1 до 100

— Таблица квадратов — это таблица, содержащая квадраты чисел. Квадрат числа — это результат умножения какого-либо числа на самого себя, то есть число, возведенное во вторую степень.

В таблице пересечение цифр слева в столбце и сверху в строке дает квадрат искомого числа. Например, нужно найти квадрат числа 15. В столбце слева берем первую цифру данного числа «1». В самой верхней строке берем вторую цифру данного числа «5». На пересечении данных цифр получаем квадрат числа 15, то есть 225.

Таблицу квадратов также можно использовать для извлечения квадратного корня — обратной операции возведения в квадрат. Например, √225=15.

— Если мы говорим о сдаче ОГЭ и ЕГЭ базового уровня по математике, то учить таблицу квадратов необязательно, так как она будет в справочном материале. А вот для ЕГЭ по профильной математике это делать нужно: справочные материалы не предоставляются. Пригодится таблица квадратов и позже, при обучении в вузе. Вот несколько советов, как это сделать.

1. Если число заканчивается на 0, его легко возвести в квадрат — необходимо только дописать пару нулей: 60 х 60 = 3600.

2. Если число заканчивается на 5, то следует умножить первую цифру (x) на (x+1) и дописать к полученному числу «25». 65 х 65 = 6 х 7 = 42 приписываем 25 и получаем 4225.

3. Можно воспользоваться формулой (a + b) 2 = a 2 + 2ab + b 2 . Как мы уже выяснили, возводить в квадрат числа, оканчивающиеся на 0, очень просто. Следовательно, а — это число, которое делится на 10, а b — остаток от деления на 10. Приведем пример. Возведем в квадрат 32. 32 можно представить как 30 (число делится на 10) и 2 (остаток от деления на 10): (30+2) 2 = 30 2 + 2 х 30 х 2 + 2 2 = 900 + 120 + 4 =1024.

Для начала нужно выучить таблицу квадратов первого десятка, так как она используется чаще всего: 121, 144, 169, 196, 225, 256, 289, 324, 361. И важно запомнить, что не бывает квадратов, последняя цифра в которых 2, 3, 7, 8. Также часто используются квадраты таких чисел как 21, 24, 25, 26: они встречаются чаще других.

Выучить данные значения квадратов можно довольно быстро: попробуйте просто ежедневно выписывать значения в тетрадь.

Источник

About This Article

Did this article help you?

Как найти квадрат числа

Быстрое возведение чисел от 1 до 100 в квадрат

Правило 1 (отсекает 10 чисел)

Правило 2 (отсекает 10 чисел)

Правило 3 (отсекает 8 чисел)

Правило 4 (отсекает 8 чисел)

Правило 5 (отсекает 8 чисел)

Правило №6 (отсекает 32 числа)

Формулы (осталось 24 числа)

Таблица квадратов натуральных чисел. Формулы сокращенного умножения

Таблица квадратов от 1 до 100

Не пропустите также: