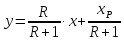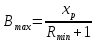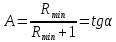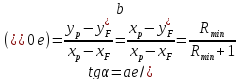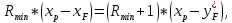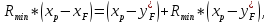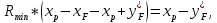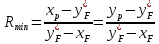Расчет колонны. Расчет массовых расходов дистиллята и кубового остатка
Страницы работы
Содержание работы
3.
Расчет колонны
3.1
Материальный баланс
Найдем массовые расходы дистиллята и кубового
остатка, решив систему уравнений:
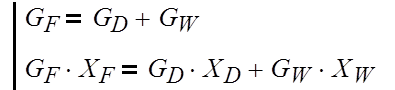
(3.1.1)
где GF,
GD, GW – соответственно массовый расход питания ,
дистиллята, кубового остатка, кг/с;
ХF, XD, XW – концентрация бензола в
массовых долях расходов питания, дистиллята и кубового остатка соответственно.
Отсюда получаем:
GD = 1,13
кг/с; GW = 2,87
кг/с;
Выразим концентрации питания, дистиллята и
кубового остатка в мольных долях:
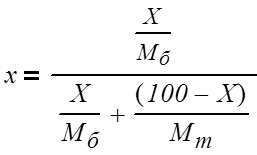
(3.1.2)
где x – концентрация в мольных долях;
X – концентрация в массовых долях;
Мб – мольная масса бензола, кг/моль;
Мт – мольная масса толуола, кг/моль;
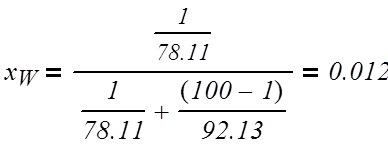 |
Найдем относительный мольный расход питания:
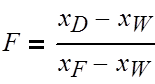
где F –
относительный мольный расход питания;
хF, хD, хW – концентрация бензола в
мольных долях расходов питания, дистиллята и кубового остатка соответственно;
На графике 1 определим по мольным концентрациям
жидкости равновесные концентрации пара бензола:
y*F
= 0,511.
Вычислим минимальное число флегмы по следующей
формуле:
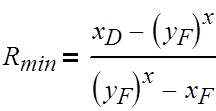
(3.1.4)
где Rmin
– минимальное число флегмы;
хF, хD – концентрация в смеси бензола в мольных
долях расходов питания, дистиллята соответственно;
yF*,
–равновесная концентрация в паре бензола в мольных долях;
Рабочее флегмовое число найдем по следующей формуле:
,
(3.1.5)
где R –
число флегмы;
b — коэффициент избытка флегмы;
Задаваясь коэффициентом избытка флегмы, найдем
рабочее число флегмы, с помощью которого построим рабочие линии для укрепляющей
и исчерпывающей части колонны по следующим формулам:
Верхняя часть:
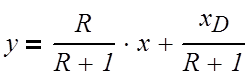
(3.1.6)
Нижняя часть:
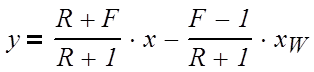
(3.1.7)
Графически определяем число теоретических ступеней (N) – график 1.
Чтобы определить оптимальное флегмовое число на
графике 2 построим зависимость N(R+1) = f(R),
где точка минимума этой кривой укажет на Rопт.
Результаты вычислений при нахождении флегмового
числа представим в таблице 1:
Таблица 1
|
b |
1,161 |
1,308 |
1,356 |
1,528 |
1,629 |
2,396 |
3,027 |
|
R |
2,4 |
2,73 |
2,83 |
3,188 |
3,4 |
5 |
6,318 |
|
N |
25 |
18 |
17 |
15 |
15 |
12 |
11 |
|
N(R+1) |
85 |
67,14 |
65,11 |
62,82 |
66 |
72 |
80,498 |
Rопт
= 3,188 при
N = 15
Уравнения рабочей линии:
укрепляющая часть:
исчерпывающая часть:
3.2 Определение скорости
пара и диаметра колонны
Найдем средние концентрации жидкости:
верхняя часть:
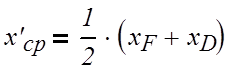
(3.2.1)
где х`ср, хF, хD – соответственно средняя концентрация верхней части колонны и
концентрация бензола в мольных долях питания и дистиллята;
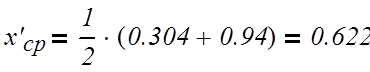 |
нижняя часть:
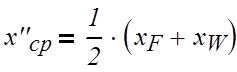
(3.2.2)
где х«ср, хF, хW – соответственно средняя концентрация нижней части колонны и
концентрация бензола в мольных долях питания и кубового остатка;
Средние концентрации пара вычислим по уравнению
рабочей линии:
верхняя часть:
нижняя часть:
Определим средние температуры пара по диаграмме
(график 3):
укрепляющая часть:
приy`ср =
0,698 t`ср = 92,7°C
исчерпывающая часть:
приy«ср = 0,246 t«ср
= 104,4 °C
Средние мольные массы и
плотности пара:
верхняя часть:
,
(3.2.3)
где М`ср – средняя мольная масса пара верхней части колонны, кг/моль;
y`ср – средняя концентрация пара верхней части колонны;
Мб – мольная масса бензола, кг/моль;
Мт – мольная масса толуола, кг/моль;
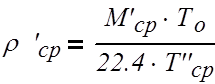
(3.2.4)
где r`ср – средняя плотность пара
в верхней части колонны, кг/м3;
Т0 —
температура при нормальных условиях, К;
Т`ср
— температура пара в верхней части колонны, К;
нижняя часть:
,
(3.2.5)
Похожие материалы
- Расчет ректификационной колонны
- Расчет теплообменного аппарата для нагрева 4 кг/с 27 % раствора бензола в толуоле от 18 до 97,9 градусов
- Расчёт и подбор теплообменной аппаратуры для подогревания 5.5 кг/с 28%-го раствора ацетона в воде от 20 до 69 градусов
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Простая
перегонка заключается в постепенном
испарении жидкости и конденсации
образующихся паров. Рассмотрим
периодически действующую перегонку.
В куб залита жидкая смесь. Составим
уравнение материального баланса.
Пусть
в момент времени τ в
кубе L
кг смеси, х –
концентрация НК в смеси, Lх –
количество НК в смеси.
За
время dτ испарится dL кг
смеси и концентрация уменьшится на dx.
При этом образуется dL кг
пара, равновесного с жидкостью и имеющего
концентрацию у*;
dLy* –
количество НК в паре. В кубе останется
остаток (L
– dL)
кг с концентрацией (х
– dx).
Тогда
уравнение материального баланса по
НК:
Lx
= (L–dL)(x–dx)+dLy*;
Раскроем
скобки: Lх
= Lх–
dLх–
Ldx+ dLdx+ dLy*,
после
сокращения получим: dL(y*–х) = Ldx,
разделим
переменные:
Это
дифференциальное уравнение проинтегрируем
от L
= F (количество
исходной смеси) до L
= W (количество
остатка) и по х от хF до хW (хF –
концентрация НК в исходной
смеси; хW –концентрация
в остатке).
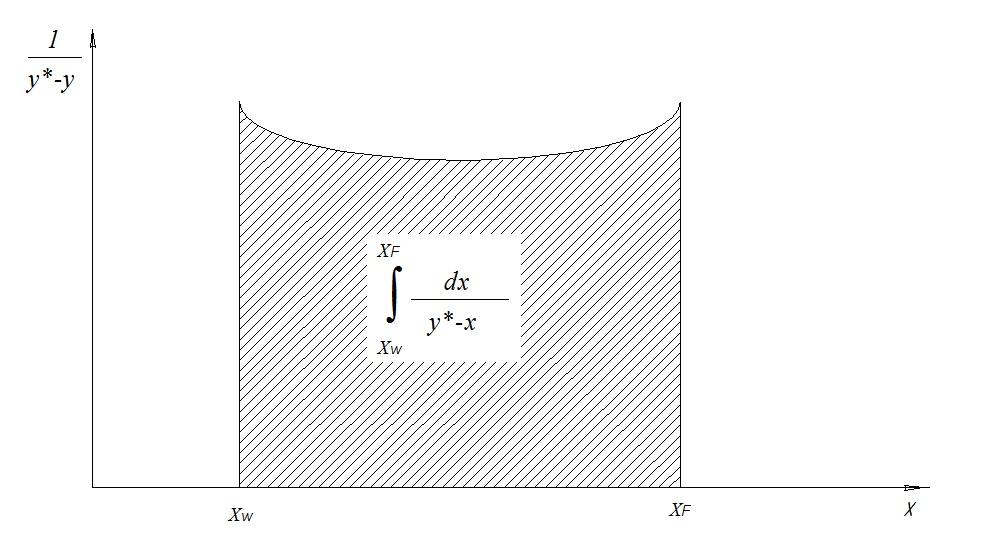
Тогда:
∫ dL/L = ∫ dx/(y* –
х); ln(F/W) = ∫ dx/(y* –
х) – W хW хW
– уравнение
простой перегонки.
Вид
функции у*
= f(x) определяется
формой кривой равновесия и не может
быть установлен аналитически. Поэтому
правую часть интегрируют графически.
Из
уравнения можно получить W,
зная F и хF, хW.
Средний состав дистиллята хр можно
определить из уравнения материального
баланса по НК:
FхF =
WхW +
(F – W) (хр)ср. ,
где
хр =
(FхF –
WхW)/(F
– W).
Простая
перегонка применяется для смесей,
компоненты которых сильно различаются
по летучести, простая перегонка – это
довольно грубое предварительное
разделение смесей.
Вопрос
№ 15. Вывести уравнения рабочих линий
ректификационной колонны непрерывного
действия.
Делаем
подстановку в 1 уравнение:
Укрепляющая
часть колонны. Количество жидкости
(флегмы), стекающей по этой части колонны
Количество
паров, поднимающихся по колонне
В
том же сечение колонны состав жидкости
(флегмы) , поступающей из дефлегматора,
Подставляя
значения L,
G,
yк,
xк
,
получаем:
Откуда
—
эта зависимость является уравнением
рабочей линии укрепляющей части колонны.
Количество
жидкости, стекающей по исчерпывающей
части колонны, составит:
Количество
пара, проходящего через нижнюю часть
колонны, равно количеству пара,
поднимающегося по верхней (укрепляющей)
ее части. Следовательно:
Для
низа колонны состав удаляющейся жидкости
(остатка) x’к=xw
и, согласно допущению, состав поступающего
сюда из кипятильника пара y’н=
yw
=
xw
. Подставив значения L’,
G’,
x’к
, y’н
в первое уравнение, получим:
После
приведения к общему знаменателю и
сокращения подобных членов находим:
эта
зависимость является уравнением рабочей
линии исчерпывающей части колонны.
16. Вывести уравнение рабочей линии для укрепляющей части ректификационной колонны. Описать, как строят рабочие линии на диаграмме y-X, сформулировав необходимые допущения.
Упрощающие
допущения графического метода анализа
работы и расчета ректификационной
колонны.
-
Молярные
теплоты испарения компонентов при
одной и той же температуре приблизительно
одинаковы (правило Трутона), поэтому
каждый киломоль пара при конденсации
испаряет 1 кмоль жидкости. Следовательно
количество поднимающихся паров (в
киломолях) в любом сечении колонны
одинаково; -
В
дефлегматоре не происходит изменения
состава пара. Если весь пар конденсируется
в дефлегматоре, то это положение
полностью соответствует реальным
условиям. Следовательно, состав пара,
уходящего из ректификационной колонны,
равен составу дистиллята, т.е.
;
-
При
испарении жидкости в кипятильнике не
происходит изменения ее состава.
Следовательно, состав пара, образующегося
в кипятильнике, соответствует составу
кубового остатка, т.е.;
-
Теплоты
смешения компонентов разделяемой
смеси равны 0.
Также,
при этом перед подачей в колонну смесь
подогревают до температуры кипения
жидкости в том сечении колонны, в которое
она поступает.
Вывод
уравнения рабочей линии для укрепляющей
части ректификационной колонны
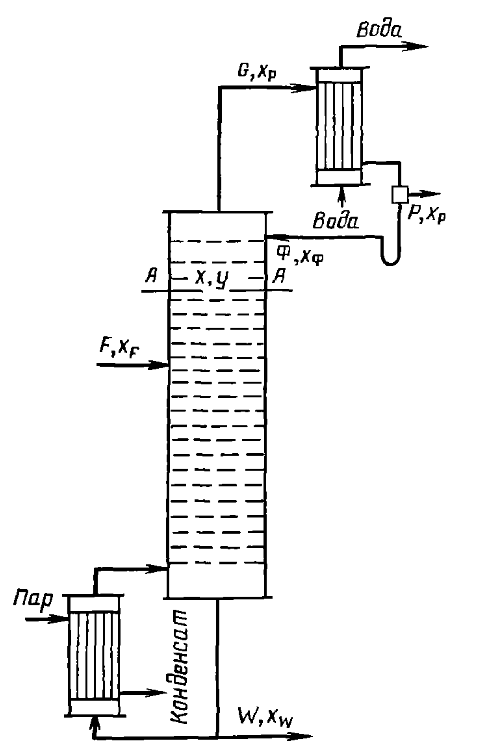
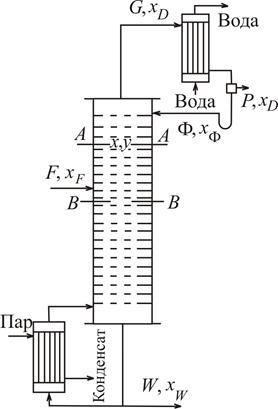
Обозначения:
-
F,
xF
— поток
(кмоль/с) и концентрация (молярные доли)
НК исходной смеси; -
P,
xP
— поток и концентрация НК дистиллята; -
W,xW
— поток
и концентрация НК кубового остатка; -
Ф,xФ
–
поток
и концентрация НК флегмы; -
G
–
количество пара (кмоль/с), выходящего
из колонны.
Материальный
баланс колонны по всему потоку:
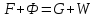
при
получаем
Материальный
баланс по низкокипящему компоненту:
Для
укрепляющей части колонны возьмем
произвольное сечение А-А (см. рис),
которому соответствуют текущие
концентрации x
и y,
и составим материальный баланс по НК
для верха этой колонны:
откуда
где
–
количество флегмы, стекающей в верхней
части колонны.
Количество
поднимающихся по колонне паров:
С
учетом
(см допущение 2), поставляем ур-я (3) и (4)
в ур-е (2). Получаем:
Таким
образом, уравнение рабочей линии
укрепляющей части колонны:
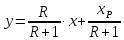
Порядок
построения рабочих линий ректификационной
колонны
-
Откладываем
на горизонтальной оси значения
;
-
Строим
на диагонали точки
и
;
-
Проводим
вертикаль при
до значения
;
-
Откладываем
на вертикальной оси отрезок
;
-
Соединяем
точку на вертикальной оси, полученную
по отрезку В,
и точку на диагонали
пунктирной линией; -
На
пересечении пунктирной линии и вертикали
(при
)
получаем точку пересечения рабочих
линий (точку питания); -
Соединяя
точку пересечения рабочих линий с
точкой
,
получаем рабочую линию верхней части
колонны; -
Соединяя
точку пересечения рабочих линий с
точкой
,
получаем рабочую линию нижней части
колонны.
17.
Вывести уравнения рабочих линий для
ретификационной колонны непрерывного
действия при постоянстве расходов фаз
(с необходимыми пояснениями и допущениями).
Как зависит положение этих линий на
диаграмме у-х от флегмового числа?
Предварительно
принимаются следующие основные
допущения, мало искажающие действительный
процесс, но существенно упрощающие его
анализ и расчет:
1.
Молярные теплоты испарения компонентов
при одной и той же температуре
приблизительно одинаковы (правило
Трутона), поэтому каждый киломоль пара
при конденсации испаряет 1 кмоль
жидкости. Следовательно, количество
поднимающихся паров (в киломолях) в
любом сечении колонны одинаково.
2.
В дефлегматоре не происходит изменения
состава пара. Если весь пар конденсируется
в дефлегматоре, то это положение
полностью соответствует реальным
условиям. Следовательно, состав пара,
уходящего из ректификационной колонны,
равен составу дистиллята, т.е. yD = xD.
3.
При испарении жидкости в кипятильнике
не происходит изменения ее состава.
Следовательно, состав пара, образующегося
в кипятильнике, соответствует составу
кубового остатка, т.е. yW = xW.
4.
Теплоты смешения компонентов разделяемой
смеси равны нулю.
При
этом предполагается, что перед подачей
в колонну смесь подогревают до температуры
кипения жидкости в том сечении колонны,
в которое она поступает.
Расчетная
схема установки представлена на рис.
3.15.
Рис.
3.15. К выводу уравнения материального
баланса
Введены
следующие обозначения (рис. 3.15):
F, xF –
поток (кмоль/с) и концентрация (молярные
доли) НК исходной смеси;
P, xD –
поток и концентрация НК дистиллята;
W, xW –
поток и концентрация НК кубового
остатка;
Ф, xФ –
поток и концентрация НК флегмы;
G –
количество пара (кмоль/с), выходящего
из колонны.
Тогда
материальный баланс колонны по всему
потоку
но G = P +
Ф, и поэтому
F = P + W.
(3.8)
Материальный
баланс по низкокипящему компоненту
(3.9)
Уравнения
рабочих линий. Поскольку
условия работы укрепляющей и исчерпывающей
частей ректификационной колонны
различны, то рассмотрим материальные
балансы для них отдельно.
Для укрепляющей части
колонны возьмем произвольное
сечение А – А (рис.
3.15), которому соответствуют текущие
концентрации x и y,
и составим материальный баланс по НК
для верха этой части колонны:
откуда
(3.10)
где L
– количество
флегмы, стекающей в верхней части
колонны.
Причем
(3.11)
где R –
флегмовое число, равное отношению
количества флегмы к количеству
отбираемого из колонны дистиллята:
Количество
поднимающихся по колонне паров
(3.12)
Так
как по принятому допущению yD = xD,
то уравнение (3.10) при подстановке в него
соответствующих значений L и G принимает
вид
откуда
получаем уравнение рабочей линии
укрепляющей части колонны:
(3.13)
При x = xD y = xD,
т.е. рабочая линия укрепляющей части
колонны пересекает диагональ с
абсциссой xD,
что и следовало ожидать, учитывая второе
допущение.
Обозначим ,
а .
Тогда уравнение (3.13) примет вид соотношения
которое
является уравнением прямой линии. В
нем А –
тангенс угла наклона a рабочей линии к
оси абсцисс, а В –
отрезок, отсекаемый рабочей линией на
оси ординат (рис. 3.16, а).
При
выводе уравнений рабочей
линии исчерпывающей части
колонны следует учитывать, что количество
орошения этой части колонны увеличивается
на величину расхода F исходной
смеси. Рассмотрим материальный баланс
для низа исчерпывающей части колонны
– ниже произвольного сечения В – В (рис.
3.15); текущие концентрации НК в фазах x и y .
Обозначим
количества поднимающегося по нижней
части колонны пара ,
а стекающей флегмы – .
Тогда
Рис.
3.16. К выводу уравнений рабочих линий
верхней (а)
и нижней (б)
частей ректификационной колонны
Если
обозначить через то
Количество
стекающей по нижней части колонны
флегмы Количество
поднимающегося по колонне пара не
меняется, т.е.
откуда
Тогда
с учетом того, что yW = xW,
получим
После
соответствующих преобразований имеем
(3.14)
где (рис.
3.16, б); –
отрезок, отсекаемый рабочей линией на
оси ординат.
При x = xW y = xW,
т.е. рабочая линия исчерпывающей части
колонны проходит через точку, лежащую
на диагонали с абсциссой xW.
Теперь выясним, где же эти линии
пересекаются.
Ордината
точки пересечения, определяемая по
уравнениям (3.13) и (3.14), будет одинаковой.
Следовательно, можно приравнять правые
части этих уравнений:
или
Решая
последнее выражение относительно
абсциссы с координатой x,
после простейших преобразований
получаем x = xF,
т.е. абсцисса точки пересечения рабочих
линий равна составу исходной смеси
(т.е. эта точка соответствует сечению,
на уровне которого подают питание в
колонну). После этого можно построить
рабочие линии для укрепляющей и
исчерпывающей частей колонны.
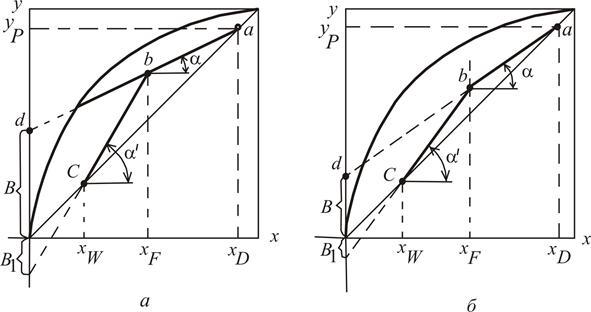
На
оси абсцисс откладывают заданные
концентрации xF, xD, xW и
находят точки а и с (рис.
3.16). Если величина R задана,
то на оси ординат откладывают отрезок и
соединяют точку d c
точкой а.
Проведя вертикаль из точки xF до
пересечения с линией ad,
находят точку b пересечения
рабочих линий и соединяют ее с точкой с.
Таким образом, получают рабочие
линии ab –
для укрепляющей и bc –
для исчерпывающей частей колонны.
18.
Метод расчёта массообменных колонных
аппаратов со ступенчатым контактом
фаз, основанный на уравнении массопередачи.
Связь локальной эффективности по Мерфри
с числом единиц переноса для различных
случаев структуры потоков фаз.
Расчет
колонных массообменных аппаратов. В
основном распространены противоточные
аппараты. Рассмотрим колонный аппарат
на примере абсорбции
Допущения:
-
Рассматривается
перенос одного компонента, остальные
компоненты считаем инертными -
Фазы
движутся по модели идеального вытеснения.
Материальный
баланс для всего аппарата:
(1)
(2)
(3)
(4)
Уравнение
(4) уже не является независимым, представляя
собой сумму первых трёх уравнений.
Материальный
баланс для верхней части аппарата:
(5)
(6)
Аналогично
для нижней части аппарата:
(6)
Уравнения
(6) – это уравнения рабочих линий
(связывают рабочие концентрации в
фазах)
(7)
(8)
Тарельчатая
колонна.
фаз ступенчатый.
(9)
(10)
(10)
Расчёт
аппаратов с непрерывной поверхностью
контакта фаз
Два
основных метода расчёта высоты колонных
аппаратов:
-
метод
теоретических ступеней -
метод,
основанный на уравнении массопередачи
В
результате технологического расчёта
получают:
-
высоту
аппарата (высота насадки), число тарелок
(высота тарельчатой части) -
сечение
аппарата (диаметр)
Объемный
расход сплошной фазы
В
экстракции расходы обеих фаз.
—
фиктивная скорость
Метод
теоретической ступени разделения
Теоретическая
тарелка – это участок аппарата, который
покидают фазы, находящиеся в равновесии.
Равновесие
определяется P
и T
Дано:
абсорбция
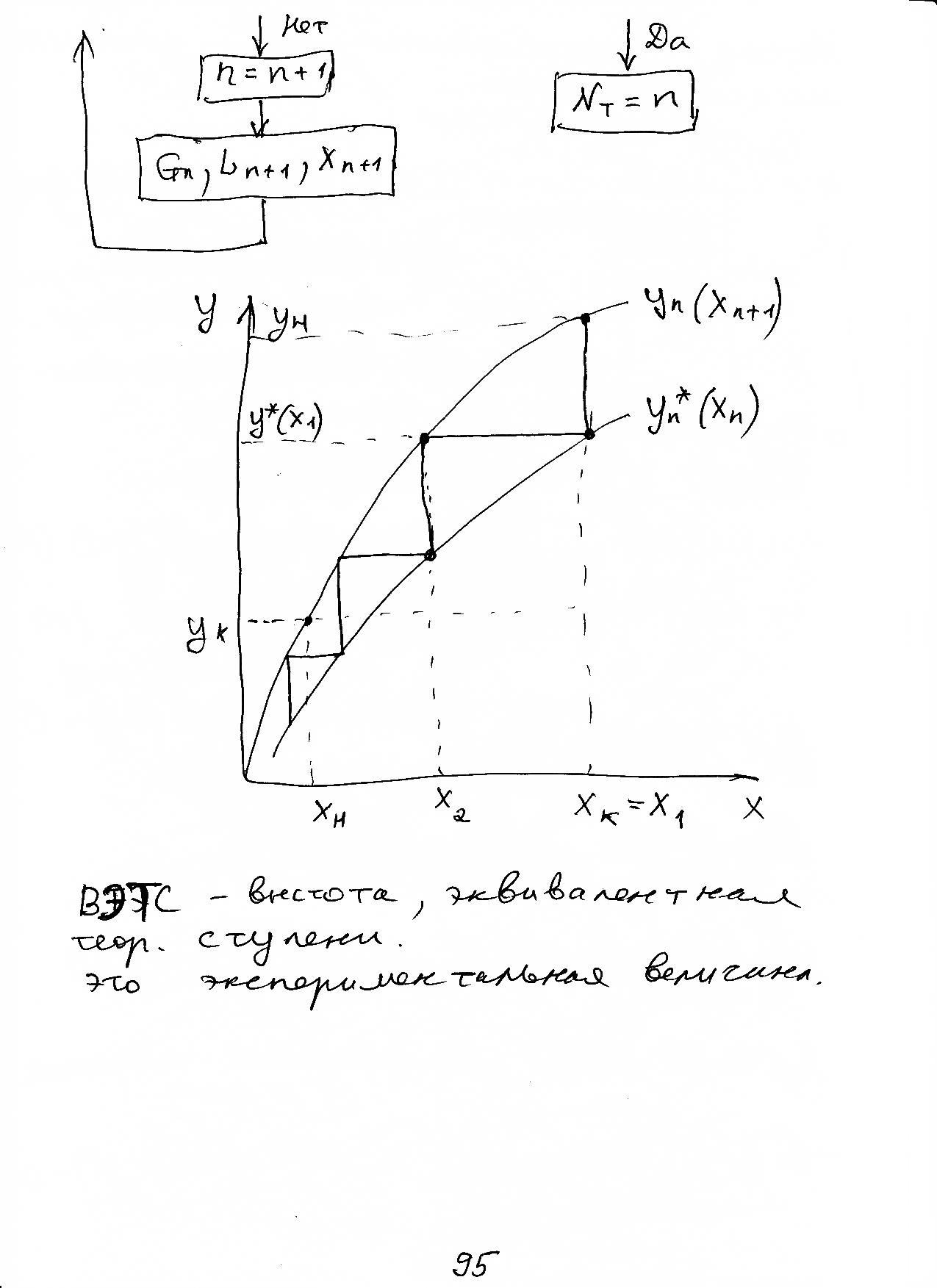
ВЭТС
– высота, эквивалентная теоретической
ступени. это экспериментальная величина
Метод,
основанный на уравнении массопередачи.

Ky
–
коэффициент массопередачи по газовой
фазе
A
– поверхность контакта фаз
(11)
(12)
По
инертному газу
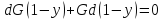
(121)
– удельная
поверхность [м2/м3]
(13)
Для
жидкой фазы
(14)
Если
линия равновесия прямая
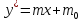
то безразлично по какому из уравнений
считать.
Выбирается
уравнение для фазы, в которой сосредоточено
основное сопротивление.
Частные
случаи:
-
Процесс
изотермический, концентрации малы
Линия
равновесия прямая
(15)
hoy
noy
noy
–
общее число единиц переноса по газовой
фазе
hoy
–
высота единиц переноса
– равновесная
линия прямая
Уравнение
рабочей линии
(для
верхней части) (16)
(для
нижней части) (17)
Fm
– фактор
массопередачи
Отношение
наклона равновесной линии
к
наклону рабочей линии
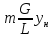
=Fm
(18)
-
Fm=1
Наклон
равновесной и рабочей линий одинаков
(из
16)
(из
17)
(19)
-
Концентрации
не малы, процесс изотермический,
коэффициенты массопередачи слабо
зависят от концентрации
(20)
Ограничений
на кривизну линий не накладывается
Для
постоянного Ky
необходимо,
чтобы
Если
, то следует записать по жидкой фазе
(21)
Другой
случай, когда в обеих фазах МИС

(22)
(МИС+МИС)
Расчёт
высоты колонных аппаратов при ступенчатом
контакте фаз
В
тарельчатых аппаратах взаимодействие
фаз рассматривают только на тарелках.
За пределами тарелок фазы не взаимодействуют
-
Метод
теоретической тарелки
Фазы,
покидающие тарелку, находятся в состоянии
равновесия (достигли состояния
равновесия)
– приходит
на тарелку,
– покидает тарелку, Ŋ – средний КПД
ступени по колонне,
– число
реальных тарелок
-
Метод,
основанный на понятии коэффициента
массопередачи (на уравнении массопередачи)
-
КПД
Мерфри
Показывает,
во сколько реальное изменение концентрации
отличается от изменения концентрации
на теоретической тарелке
(22)
(23)
(24)
E0
–
локальная эффективность по Мерфри (без
учёта реальных факторов брызгоуноса,
байпасирующей жидкости и др.)
EMy
–
реальный
КПД Мерфри
19.
Вывести формулу для расчета минимального
флегмового числа при непрерывной
ректификации. Какие принципы используют
для оптимизации при определении
флегмового числа?
Упрощающие
допущения графического метода анализа
работы и расчета ректификационной
колонны.
-
Молярные
теплоты испарения компонентов при
одной и той же температуре приблизительно
одинаковы (правило Трутона), поэтому
каждый киломоль пара при конденсации
испаряет 1 кмоль жидкости. Следовательно
количество поднимающихся паров (в
киломолях) в любом сечении колонны
одинаково; -
В
дефлегматоре не происходит изменения
состава пара. Если весь пар конденсируется
в дефлегматоре, то это положение
полностью соответствует реальным
условиям. Следовательно, состав пара,
уходящего из ректификационной колонны,
равен составу дистиллята, т.е.
;
-
При
испарении жидкости в кипятильнике не
происходит изменения ее состава.
Следовательно, состав пара, образующегося
в кипятильнике, соответствует составу
кубового остатка, т.е.;
-
Теплоты
смешения компонентов разделяемой
смеси равны 0.
Также,
при этом перед подачей в колонну смесь
подогревают до температуры кипения
жидкости в том сечении колонны, в которое
она поступает.
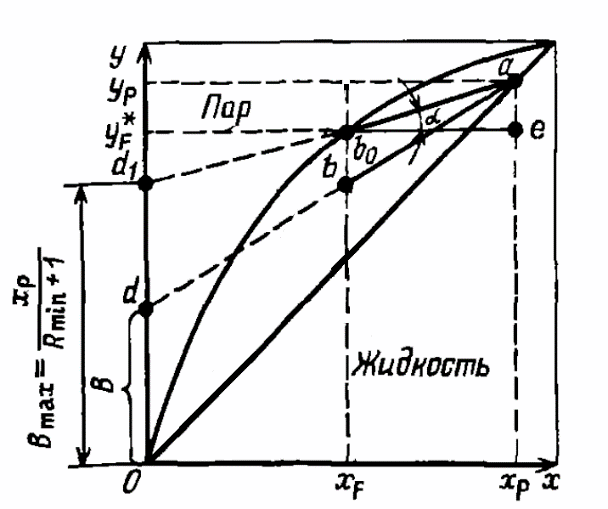
Вывод
формулы для расчета минимального
флегмового числа при непрерывной
ректификации
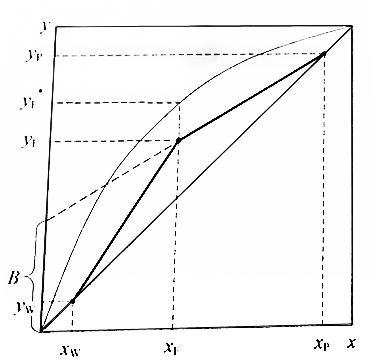
При
пересечении рабочих линий в точке b0
рабочие концентрации равны равновесным,
что возможно только при бесконечно
большой поверхности массопередачи,
так как при этом
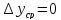
В
этом случае (линия ad1
на графике) флегмовое число должно быть
минимальным, а величина отрезка B
– максимальной.
Уравнение
рабочей линии верхней части колонны:
Преобразовав
уравнение рабочей линии верхней части
колонны к линейному виду, получим:

где

В
нашем случае:
или
(Bmax
определяется графически)
Из
уравнения рабочей линии верхней части
колонны для рассматриваемого случая:
Откуда
последует, что:
Решая
уравнение относительно Rmin,
получим:
Тепловой баланс
Количество теплоты, выделяющееся при конденсации паров дистиллята, находим по уравнению:
,
где -удельная теплота испарения дистиллята, ; -флегмовое число; -массовый расход дистиллята.
Удельную теплоту испарения найдём по формуле:
Зная мольный состав дистиллята, исходной смеси и кубового остатка, по диаграмме найдём их температуры кипения:
Зная мольный состав и температуру кипения дистиллята, найдём удельную теплоту испарения:
Количество теплоты, отдаваемое дистиллятом при охлаждении, находим по формуле:
,
где -температура кипения дистиллята; -теплоёмкость дистиллята при температуре кипения.
Количество теплоты, получаемое исходной смесью, в паровом подогревателе найдём по формуле:
Количество теплоты, отдаваемое кубовым остатком в водяном холодильнике, найдём по формуле:
Найдём количество тепла, которое необходимо подвести в куб-испаритель по формуле:
Найдём расход пара в куб-испаритель.
По известному абсолютному давлению греющего пара () найдём его теплоту конденсации:
Массовый расход пара равен:
Подробный расчет холодильника кубового остатка
Температурная схема:
,
ректификация бинарный смесь жидкость
Тогда . По известному составу и средней температуре найдём необходимые параметры теплоносителя и хладагента:
а) Удельная теплоемкость кубового остатка:
б) Количество теплоты:
в) Теплоемкость воды:

Для определения ориентировочной площади теплообмена примем коэффициент теплопередачи
Определим ориентировочно площадь теплообмена:
Для обеспечения интенсивного теплообмена попытаемся подобрать аппарат с турбулентным или переходным режимом течения теплоносителей. Возьмём теплообменный аппарат типа “труба в трубе” по ГОСТ (9830-79) с диаметром кожуховой трубы и теплообменной кубовый остаток направим в кожуховую трубу, а охлаждающую воду в теплообменную трубу.
Зададимся критерием Рейнольдса для кубового остатка : Re2=10000
Эквивалентный диаметр кольцевого сечения: dэкв=0.011
Вязкость кубового остатка при его средней температуре :
Плотность кубового остатка при его средней температуре:
Найдем скорость кубового остатка:
Найдем площадь поперечного сечения:
Найдем по каталогу стандартную площадь:
Найдем по стандартной площади скорость и число Рейнольдса:
В теплообменной трубе хладагент- вода.
Зададимся критерием Рейнольдса для воды : Re1=10000
Эквивалентный диаметр кольцевого сечения: dэкв=0.03 м
Вязкость(Пас) воды при ее средней температуре :

Найдем скорость воды:
Найдем площадь поперечного сечения:
Найдем по каталогу стандартную площадь:
Найдем по стандартной площади скорость и число Рейнольдса:
Температуры стенки со сторон холодного и горячего теплоносителей будем искать с помощью метода итераций. Суть метода заключается в нахождении удельного потока теплоты со стороны хладагента и теплоносителя как функций от температуры одной из стенок теплообменника и решения уравнения графическим методом или с помощью ПК относительно температуры стенки.
Сначала рассмотрим холодный теплоноситель — воду. Найдем для нее теплофизические свойства и при ее средней температуре:
Теплопроводность:
Теплоемкость (Дж/кгК):
Вязкость (Пас):
=7.482*10-4
Плотность (кг/м3):
Определим критерий Прандтля для кубового остатка по формуле:
.
Зададимся температурой стенки со стороны хладагента tстхол=37,115
Найдем теплофизические параметры и критерий Прандтля при температуре стенки хладагента:
Теплопроводность:
Теплоемкость (Дж/кгК):
Вязкость (Пас):
=6,899 10-4
Представим критерий Прандтля при температуре стенки как функцию от этой температуры, это позволяют сделать функциональные зависимости теплофизических свойств компонентов смеси от температуры:
Так как режим течения жидкости турбулентный, то критерий Нуссельта для водыбудем находить по формуле:
Выразим коэффициент теплоотдачи как функцию от температуры соответствующей стенки:
,
Зная коэффициенты теплоотдачи можно выразить удельный тепловой поток как функцию от температуры соответствующей стенки:
Выразим температуру горячей стенки () как функцию от температуры холодной стенки (). Это позволяет сделать соотношение:
Коэффициент теплопроводности стали, берём из [3] , среднее значение тепловой проводимости загрязнений стенок берём из [3] для смеси паров бензол — толуол и воды среднего качества.
Решив уравнение, находим .
Теперь рассмотрим горячий теплоноситель — кубовый остаток. Найдем его теплофизические свойства при его средней температуре.
Теплопроводность:
Теплоемкость (Дж/кгК):
Определим критерий Прандтля для кубового остатка по формуле:
.
Найдем теплофизические параметры и критерий Прандтля при температуре стенки горячего теплоносителя ():
Вязкость
Теплопроводность
Теплоемкость
Представим критерий Прандтля при температуре стенки как функцию от этой температуры, это позволяют сделать функциональные зависимости теплофизических свойств компонентов смеси от температуры:
Так как режим течения жидкости можно считать турбулентным, то критерий Нуссельта для кубового остатка будем находить по формуле (для кубового остатка):
Выразим коэффициент теплоотдачи как функцию от температуры соответствующей стенки:
,
Зная коэффициенты теплоотдачи можно выразить удельный тепловой поток как функцию от температуры соответствующей стенки:
Потоки равны с погрешностью
Найдём коэффициент теплопередачи:
Расчетная площадь поверхности теплопередачи:
Теплообменник обладает следующими характеристиками:
Тип “труба в трубе”, диаметр кожуховой трубы , диаметр теплообменной трубы , длина одной секции — 3м, всего 22 секции.
Приближенный расчет теплообменников
1. Паровой подогреватель исходной смеси.
Температурная схема:
,
Тогда . По известному составу и средней температуре смеси найдём её удельную теплоёмкость:
Найдём количество теплоты, передаваемое паром исходной смеси:
Теплоту конденсации пара найдём по его абсолютному давлению:
Определим расход греющего пара:
Ориентировочную поверхность теплообмена найдём по уравнению:
Приблизительное значение коэффициента теплопередачи возьмём из [3]: . Тогда ориентировочная поверхность теплообмена будет равна:
По площади теплообмена подберём подходящий теплообменный аппарат:
-«труба в трубе»;
-диаметр труб 133?6мм и 219?6мм;
-площадь теплообмена 3,72 ;
-длинна труб 9м.
2. Дефлегматор-конденсатор
Температурная схема:
,
Тогда . По известному составу и средней температуре смеси найдём её удельную теплоёмкость:
Определим расход охлаждающей воды:
Ориентировочную поверхность теплообмена найдём по уравнению:
Приблизительное значение коэффициента теплопередачи возьмём из [3]: . Тогда ориентировочная поверхность теплообмена будет равна:
По площади теплообмена подберём подходящий теплообменный аппарат:
-кожухотрубный;
-диаметр труб 20?2мм;
-площадь теплообмена 11,5 ;
-длинна труб 3,0 м.
3. Куб-испаритель
Температурная схема:
,
Тогда . По известному составу и средней температуре смеси найдём её удельную теплоёмкость:
Теплоту конденсации пара найдём по его абсолютному давлению:
Определим расход греющего пара:
Ориентировочную поверхность теплообмена найдём по уравнению:
.
Приблизительное значение коэффициента теплопередачи возьмём из [3]: . Тогда ориентировочная поверхность теплообмена будет равна:
По площади теплообмена подберём подходящий теплообменный аппарат:
-кожухотрубный;
-диаметр труб 20?4мм;
-площадь теплообмена 46 ;
-длинна труб 4 м.
Калькулятор простой перегонки + видео
Обновлено 01.06.2022
Просмотров 7285
function set_dimm(){
str=document.getElementById(‘fieldname3_1’).value;
str= str.replace(«[«, «»);
str= str.replace(«]», «»);
var arruyuy = str.split(‘,’);
url=»/calc.php?t1=»+arruyuy[0]*100+»&t2=»+arruyuy[1]*100+»&obem=»+document.getElementById(‘fieldname2_1’).value;
(function ($) {
$(«#field_1-3»).load(url);
//alert(url);
})(jQuery);
}
Данный калькулятор рассчитывает объем в мл.(1000мл. = 1л.) и содержание спирта в продукте после перегонки без укрепления. Сухопарники, барботеры и прочее в расчете не участвуют, только паропровод и холодильник.
Для расчета следует задать исходный объем в кубе и температурный диапазон перегонки.
Если для вас сложно ориентироваться по температурам, перевести содержание спирта в температуру можно калькулятором спиртоузности (раздел Обратный перевод).
На выходе будут доступны следующие данные:
- Начальная спиртоузность. Вычесляется по температуре закипания.
- Будет отобрано — расчетный объем продукта на выходе.
- Спиртоузностью — содержание спирта в полученном продукте.
- Абсолютного спирта в отборе — содержание спирта в миллилитрах.
- Останется в кубе — кубовый остаток. Позволяет контролировать покрытие тэна.
Для дистилляции с отбором голов и хвостов воспользуйтесь калькулятором дробной перегонки.

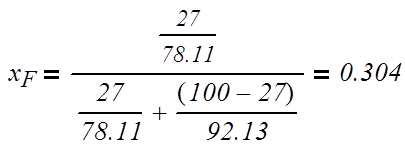
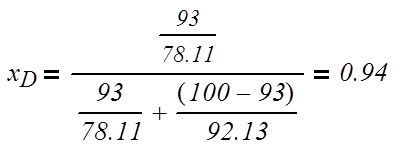

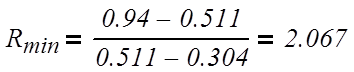
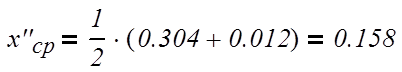
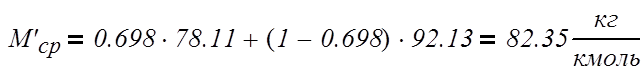
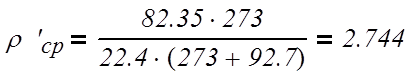
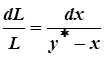

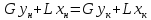
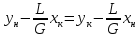
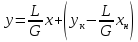
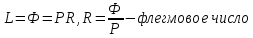

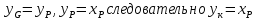
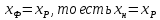
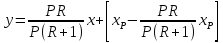
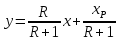
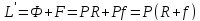
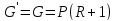
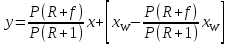
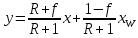
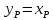 ;
; ;
;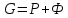

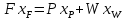

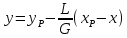
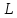
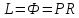

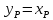
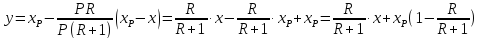
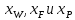 ;
;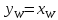
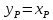 ;
;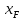
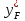 ;
;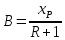 ;
;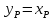
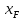 )
)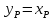 ,
,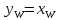 ,
,
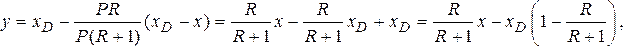
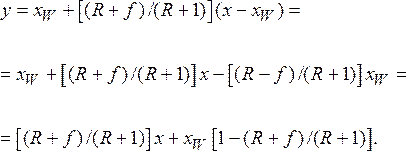
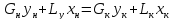
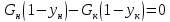
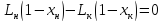

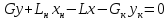


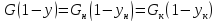
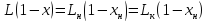
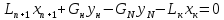
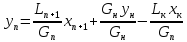


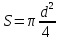
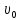
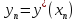
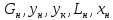
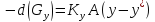
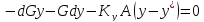
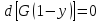
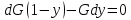
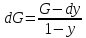
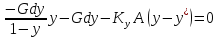
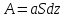

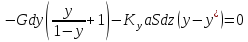
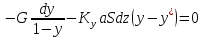
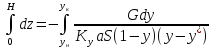
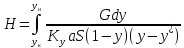
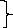

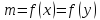
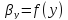
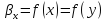


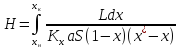
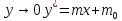

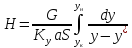

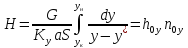
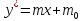
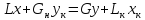
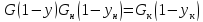
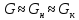
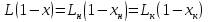
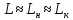
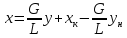
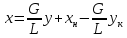
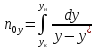




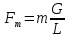
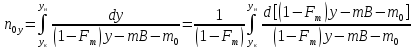
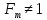
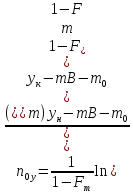
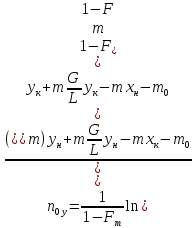
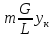
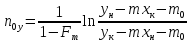
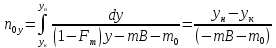
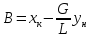
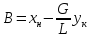
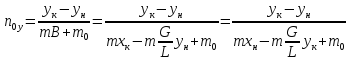
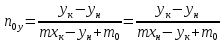
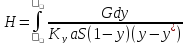
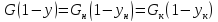
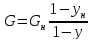
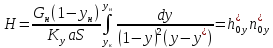

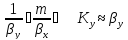


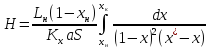
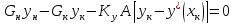
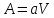
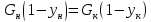
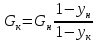
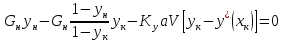
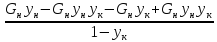
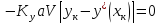
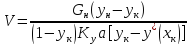
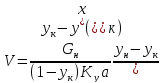
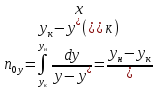


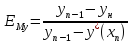
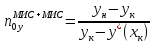
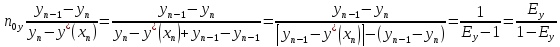
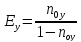

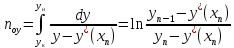
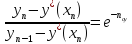
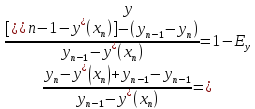
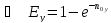
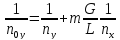
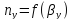
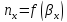
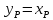 ;
;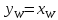 ;
;