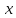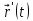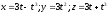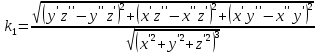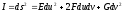оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Основная формула для вычисления кривизны плоской кривой
Кривизна представляет собой количественную характеристику степени изогнутости плоской кривой.
Построим касательную к кривой в точке $M$. При переходе по кривой из точки $M$ в некоторую соседнюю точку $N$, касательная в текущей точке поворачивается на угол $Delta phi $.
Определение
Отношение угла $Delta phi $ к длине дуги $Delta s$ между точками $M$ и $N$ называется средней кривизной дуги $K_{A@} =frac{Delta phi }{Delta s} $.
Средняя кривизна характеризует среднюю изогнутость на всей дуге. Но на отдельных участках кривой значения кривизны могут испытывать значительные отклонения от среднего значения. Здравый смысл подсказывает, что чем короче дуга, тем лучше она характеризуется средней кривизной. А точнее всего характеризовать изогнутость кривой непосредственно в самой точке $M$.
Кривизной $K$ данной кривой в данной точке $M$ называется предел средней кривизны дуги $cup MN$ при неограниченном приближении точки $N$ к точке $M$, то есть $K=mathop{lim }limits_{Delta sto 0} frac{Delta phi }{Delta s} =frac{dphi }{ds} $. Поскольку считается, что кривизна кривой — величина положительная, то $K=left|frac{dphi }{ds} right|$.
Вычисление кривизны плоской кривой
При произвольном параметрическом задании кривой $x=xleft(tright)$ и $y=yleft(tright)$ имеет место выражение $s’_{t} =sqrt{left(x’_{t} right)^{2} +left(y’_{t} right)^{2} } $.
Теперь для выражения $K = frac {d phi}{ds} = frac {d phi / dt}{ds/dt}= frac{phi ‘_{t} }{s’_{t} } $ необходимо вычислить $phi ‘_{t} $.
Так как по определению производной $tgphi =frac{y’_{t} }{x’_{t} } $, то $phi =arctgfrac{y’_{t} }{x’_{t} } $, откуда $phi ‘_{t} =frac{1}{1+left(frac{y’_{t} }{x’_{t} } right)^{2} } cdot frac{left(y’_{t} right)^{{‘} } _{t} cdot x’_{t} -left(x’_{t} right)^{{‘} } _{t} cdot y’_{t} }{left(x’_{t} right)^{2} } $.
После преобразований получаем: $phi ‘_{t} =frac{left(y’_{t} right)^{{‘} } _{t} cdot x’_{t} -left(x’_{t} right)^{{‘} } _{t} cdot y’_{t} }{left(x’_{t} right)^{2} +left(y’_{t} right)^{2} } $.
Теперь формула для кривизны кривой приобретает окончательный вид: $K=frac{left(y’_{t} right)^{{‘} } _{t} cdot x’_{t} -left(x’_{t} right)^{{‘} } _{t} cdot y’_{t} }{sqrt{left(left(x’_{t} right)^{2} +left(y’_{t} right)^{2} right)^{3} } } $.
Если кривая задана в явном виде $y=fleft(xright)$, то выбирая в качестве параметра $t=x$, получаем $K=frac{left(y’_{x} right)^{{‘} } _{x} }{sqrt{left(1+left(y’_{x} right)^{2} right)^{3} } } $.
Если кривая задана в полярных координатах $rho =rho left(phi right)$, то принимая в качестве параметра $t=phi $ и учитывая формулы $x=rho cdot cos phi $ и $y=rho cdot sin phi $, получаем:
[x’_{phi } =left(rho cdot cos phi right)^{{‘} } _{phi } =rho ‘_{phi } cdot cos phi -rho cdot sin phi ;]
[left(x’_{phi } right)^{{‘} } _{phi } =left(rho ‘_{phi } cdot cos phi -rho cdot sin phi right)^{{‘} } _{phi } =left(rho ‘_{phi } right)^{{‘} } _{phi } cdot cos phi -2cdot rho ‘_{phi } cdot sin phi -rho cdot cos phi ;]
[y’_{phi } =left(rho cdot sin phi right)^{{‘} } _{phi } =rho ‘_{phi } cdot sin phi +rho cdot cos phi ;]
[left(y’_{phi } right)^{{‘} } _{phi } =left(rho ‘_{phi } cdot sin phi +rho cdot cos phi right)^{{‘} } _{phi } =left(rho ‘_{phi } right)^{{‘} } _{phi } cdot sin phi +2cdot rho ‘_{phi } cdot cos phi -rho cdot sin phi .]
После подстановки имеем: $K=frac{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot left(rho ‘_{phi } right)^{{‘} } _{phi } }{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } } $.
Задачи вычисления кривизны плоской кривой.
Задача 1
Определить кривизну параболы $y=2cdot x^{2} $ в её произвольной точке $Mleft(x,yright)$, а также в точке $M_{1} left(0,0right)$.
Вычисляем первую и вторую производные функции $y=2cdot x^{2} $:
[y’=left(2cdot x^{2} right)^{{‘} } =4cdot x; y»=left(4cdot xright)^{{‘} } =4. ]
Подставляем полученные выражения в формулу для кривизны:
[K=frac{y»}{sqrt{left(1+left(y’right)^{2} right)^{3} } } =frac{4}{sqrt{left(1+left(4cdot xright)^{2} right)^{3} } } =frac{4}{sqrt{left(1+16cdot x^{2} right)^{3} } } .]
В точке $M_{1} left(0,0right)$ имеем $K=4$.
Задача 2
Определить кривизну параболы $y^{2} =frac{1}{2} cdot x$ в её произвольной точке $Mleft(x,yright)$, а также в точке $M_{1} left(0,0right)$. Сравнить результат решения с результатом, полученным в задаче 1.
Вычисляем первую и вторую производные функции $y^{2} =frac{1}{2} cdot x$:
$left(y^{2} right)^{{‘} } =left(frac{1}{2} cdot xright)^{{‘} } $; $2cdot ycdot y’=frac{1}{2} $, откуда $y’=frac{1}{4cdot y} $;
$left(2cdot ycdot y’right)^{{‘} } =left(frac{1}{2} right)^{{‘} } $; $y’cdot y’+ycdot y»=0$, откуда $y»=-frac{1}{16cdot y^{3} } $.
Подставляем полученные выражения в формулу для кривизны:
[K=frac{y»}{sqrt{left(1+left(y’right)^{2} right)^{3} } } =frac{frac{1}{16cdot y^{3} } }{sqrt{left(1+frac{1}{16cdot y^{2} } right)^{3} } } =frac{4}{sqrt{left(1+16cdot y^{2} right)^{3} } } .]
В точке $M_{1} left(0,0right)$ имеем $K=4$.
Полученный результат по форме и численно совпадает с результатом, полученным в задаче 1. Действительно, кривые обеих задач совпадут, если систему координат второй задачи повернуть на $frac{pi }{2} $ против часовой стрелки. Естественно, что кривизна кривой не меняется при преобразованиях её системы координат.
«Кривизна и её вычисление» 👇
Задача 3
Найти кривизну параметрически заданной линии $left{begin{array}{c} {x=2cdot cos left(3cdot tright)} \ {y=3cdot sin left(2cdot tright)} end{array}right. $ в точке $t=frac{pi }{6} $.
Находим производные:
[x’_{t} =left(2cdot cos left(3cdot tright)right)^{{‘} } _{t} =-6cdot sin left(3cdot tright);]
[x»_{tt} =left(-6cdot sin left(3cdot tright)right)^{{‘} } _{t} =-18cdot cos left(3cdot tright);]
[y’_{t} =left(3cdot sin left(2cdot tright)right)^{{‘} } _{t} =6cdot cos left(2cdot tright);]
[y»_{tt} =left(6cdot cos left(2cdot tright)right)^{{‘} } _{t} =-12cdot sin left(2cdot tright).]
Вычисляем значения производных в заданной точке $t=frac{pi }{6} $:
[x’_{t} left(frac{pi }{6} right)=-6cdot sin left(3cdot frac{pi }{6} right)=-6;]
[x»_{tt} left(frac{pi }{6} right)=-18cdot cos left(3cdot frac{pi }{6} right)=0;]
[y’_{t} left(frac{pi }{6} right)=6cdot cos left(2cdot frac{pi }{6} right)=3;]
[y»_{tt} left(frac{pi }{6} right)=-12cdot sin left(2cdot frac{pi }{6} right)=-6cdot sqrt{3} .]
Полученные значения подставляем в формулу для кривизны:
[K=frac{y»_{tt} cdot x’_{t} -x»_{tt} cdot y’_{t} }{sqrt{left(left(x’_{t} right)^{2} +left(y’_{t} right)^{2} right)^{3} } } =frac{-6cdot sqrt{3} cdot left(-6right)-0cdot 3}{sqrt{left(left(-6right)^{2} +left(3right)^{2} right)^{3} } } =frac{36cdot sqrt{3} }{45cdot sqrt{45} } =frac{4}{5cdot sqrt{15} } .]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Рассматриваем
регулярную поверхность
в окрестности точки

Дифференциалы

из (3.7.1) подставим в выражение (3.6.4) для
нормальной кривизны поверхности. После
сокращение на
приходим к равенству
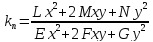
Отсюда
получаем

Дифференцируем
это равенство по
и по

Главные
направления в касательной плоскости
определяются этой системой уравнений,
если она имеет ненулевые решения, т.е.
в случае


Значение
определителя

Главные
кривизны

есть корни выписанного уравнения.
Воспользуемся теоремой Виетта:

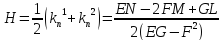
Полная
и средняя кривизны поверхности найдены
без вычисления главных кривизн.
Практическая
часть.
4.Кривая.
Кривая
задана следующим образом:
Найдем
производные первого, второго и третьего
порядков.
4.1.Найдем
уравнение касательной по формуле:
Возьмем

Найдем
производную
При
подставлении
в
получим точку Р =(0,0,0);
При
подставлении
в
получим точку
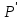
Составим
уравнение касательной для кривой

4.2.Найдем
уравнение нормальной плоскости для
кривой
по формуле:
Подставляя
уже найденные ранее данные, получаем:
4.3.Найдем
уравнение соприкасающейся плоскости
по формуле:
Раскроем
определитель по первой строке



Примем
Подставим
значения в уравнение соприкасающейся
плоскости:
Уравнение
соприкасающейся плоскости имеет вид:
8x+6y-3z-1=0.
4.4.Сосчитаем
кривизну кривой
по следующей формуле:
Подставляя
ранее полученные значения производных
первого и второго порядков в основную
формулу нахождения кривизны кривой в
координатах, получим нужную нам кривизну.
Из-за сложности в подсчетах разделим
вычисление на несколько этапов:
-
Вычисление
числителя без извлечения корня
Приведем
подобные слагаемые и извлечем корень
из получившегося выражения:
2)Вычисление
знаменателя без извлечения корня.
Извлечем
корень
Подставим
все в итоговую формулу
4.5.Вычислим кручение кривой :
Примем
t=0;
Получим

4. 6. Изображение кривой.
5. Поверхность.
Поверхность
задана следующим образом:
Вычислим
производные:
5.1. Найдем уравнение касательной плоскости, используя формулу:

Подставляя
в нее значения производных, получим:

Раскроем
определители и получим общее уравнение
искомой поверхности:
Найдем
уравнение касательной плоскости в
конкретной точке:
Выберем
произвольную точку Р(1,2,1).
Зададим
u=1,v=
Примем
a=2,k=
Подставляя
в формулу, получим:
5.2. Найдем уравнение нормали для искомой поверхности.
Раскроем
определители:
Подставляя
уже найденные ранее производные и
приводя подобные слагаемые, получим:
Найдем
уравнение нормали в конкретной точке:
Выберем
произвольную точку Р (1,1,2).
Зададим
a=2
,k=
u=1,v=

Подставим
заданные значения в уравнение:
5.3.Вычисление
первой квадратичной формы.
Найдем
частные производные:
Вычисляем
коэффициенты первой квадратичной формы
поверхности:
Детерминант
первой квадратичной формы:

Корень
из детерминанта первой квадратичной
формы:

Первая
квадратичная форма имеет вид:
Подставим
получившиеся значения в эту формулу и
получим
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
Кривизна и кручение. Натуральные уравнения кривой
Краткие теоретические сведения
Кривизна кривой
Кривизной $k$ кривой в данной точке называют модуль скорости вращения касательной по отношению к длине дуги.
Регулярная дважды дифференцируемая без особых точек кривая $gamma$, заданная векторной функцией $vec{r}=vec{r}(t)$, имеет в каждой точке определенную кривизну, причем
$$
|k(t)|=frac{|vec{r’}(t)times vec{r»}(t)|}{|vec{r'(t)}|^3}.
$$
Для кривой, заданной параметрически
$$ x=x(t), ,, y=y(t), ,, z=z(t), $$
кривизна в точке $P(t=t_0)$ находится по формуле:
$$
k^2(t_0)=frac{left| begin{array}{cc}
y’ & z’ \
y»& z» \
end{array}
right|^2+left| begin{array}{cc}
z’ & x’ \
z»& x» \
end{array}
right|^2+left| begin{array}{cc}
x’ & y’ \
x» & y» \
end{array}
right|^2}{Bigl((x’)^2+(y’)^2+(z’)^2Bigr)^3},
$$
где все производные вычисляются при $t=t_0$.
Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то векторы $vec{r’}(s)$ и $vec{r»}(s)$ перпендикулярны, причем $|vec{r’}(s)|=1$. Тогда выражение для кривизны принимает вид:
$$
k(s)= |vec{r»}(s)|.
$$
?
Что вы скажете о кривой, которая в каждой свой точке имеет нулевую кривизну?
Для плоской кривой, лежащей в плоскости $(xy)$, кривизну можно найти по формулам:
$$
begin{array}{rl}
x=x(t), y=y(t):& k = displaystylefrac{|x’y»-x»y’|}{left((x’)^2+(y’)^2right)^{3/2}}, \
y=y(x):& k = displaystylefrac{|y»|}{left(1+(y’)^2right)^{3/2}}, \
rho=rho(varphi):& k = displaystylefrac{|rho^2+2(rho’)^2-rhorho»|}{left(rho^2+(rho’)^2right)^{3/2}}.\
end{array}
$$
Кручение
Абсолютным кручением $varkappa$ кривой называют скорость вращения соприкасающейся плоскости вокруг касательной.
$$
|varkappa (t)|=frac{|(vec{r’}(t), vec{r»}(t), vec{r»’}(t))|}{|vec{r’}(t)times vec{r»}(t)|^2}.
$$
В случае естественной параметризации
$$
|varkappa(s)|=frac{|(vec{r’}(s), vec{r»}(s), vec{r»’}(s))|}{k^2(s)}
$$
Для плоской кривой кручение равно нулю: $varkappa=0$!
Натуральные уравнения кривой
Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то кривизна и кручение будут являться функциями длины дуги
$$
k=k(s), quad varkappa=varkappa(s).
$$
Система этих двух соотношений называется натуральными уравнениями кривой.
Натуральные уравнения полностью определяют форму кривой, ибо связывают инварианты, которые не меняются при преобразовании координат (при изменении положения указанной кривой в пространстве относительно системы координат).
Решение задач
Задача 1 (Феденко №351)
Найдите кривизну кривой:
$$
x=a,mbox{cos}^3t,,,y=a,mbox{sin}^3t.
$$
Задача 2 (Феденко №380)
Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=mbox{sin}x$ в точке $A(pi/2,1)$ общие касательную и кривизну.
Задача 3 (Феденко №405)
Составьте натуральные уравнения кривой:
$$
x=a(mbox{cos},t+t,mbox{sin},t), ,, y=a(mbox{sin},t-t,mbox{cos},t).
$$
Краткое решение задачи 3
$$
s=frac{at^2}{2}.
$$
$$
k=frac{1}{at}.
$$
$$
t=frac{1}{ak} Rightarrow s= frac{1}{2ak^2}.
$$
Натуральные уравнения:
$$
k=frac{1}{at},,,s=frac{at^2}{2}
$$
или
$$
k^2=frac{1}{2as}.
$$
Феденко записывает ответы через радиус кривизны:
$R=frac{1}{k}$.
Задача 4 (Феденко №486, №514)
Найдите кривизну и кручение, составьте натуральные уравнения кривой:
$$
x=a,mbox{ch}t, , y=a,mbox{sh}t, , z=a, t.
$$
Решение задачи 4
Задачу можно решать двумя способами:
1 способ. Найти $k(t), varkappa(t), s(t)$.
2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $vec{r}=vec{r}(s)$. А далее найти $k(s)$ и $varkappa(s)$.
Воспользуемся первым способом.
begin{gather*}
vec{r}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , at},\
vec{r’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , a},\
vec{r»}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , 0}\
vec{r»’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , 0}.
end{gather*}
$$
Rightarrow quad k^2(t) = frac{1}{4a^2mbox{ch}^4t}.
$$
$$
Rightarrow quad k(t) = frac{1}{2a,mbox{ch}^2t}.
$$
begin{equation*}
varkappa(t) = frac{ left|
begin{array}{ccc}
a,mbox{sh}t & a,mbox{ch}t & a \
a,mbox{ch}t & a,mbox{sh}t & 0 \
a,mbox{sh}t & a,mbox{ch}t & 0 \
end{array}
right|}{a^4cdot 2mbox{ch}^2t} = frac{1}{2a,mbox{ch}^2t}.
end{equation*}
В задаче №473 была та же кривая и мы получили, что
$$s=asqrt{2},mbox{sh},t.$$
Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения:
begin{equation*}
s=asqrt{2},mbox{sh}t=asqrt{2},sqrt{mbox{ch}^2t-1} ,, Rightarrow ,, mbox{ch}^2t=frac{s^2}{2a^2}+1 ,, Rightarrow
end{equation*}
begin{equation*}
k(s)=varkappa(s)=frac{1}{2a,mbox{ch}^2t} = frac{a}{s^2+2a^2}.
end{equation*}
Вычисления сделаны для $a>0$.
Задача 5 (Феденко №496)
Найдите функцию $f(t)$, для которой данная кривая — плоская:
$$
vec{r}(t)={a,mbox{cos}t, , a,mbox{sin}t, , f(t)}
$$
Решение задачи 5
$$
begin{array}{lll}
x=a,mbox{cos}t,, &y=a,mbox{sin}t, , &z=f(t),\
x’=-a,mbox{sin}t, , &y’=a,mbox{cos}t, , &z’=f'(t),\
x»=-a,mbox{cos}t, , &y»=-a,mbox{sin}t, , &z»=f»(t),\
x»’=a,mbox{sin}t, , &y»’=-a,mbox{cos}t, , &z»’=f»'(t).
end{array}
$$
Для плоской кривой кручение равно нулю:
begin{equation*}
varkappa(t) = left|
begin{array}{rrr}
-a,mbox{sin}t & a,mbox{cos}t & f'(t) \
-a,mbox{cos}t & -a,mbox{sin}t & f»(t) \
a,mbox{sin}t & -a,mbox{cos}t & f»'(t) \
end{array}
right| = left( f'(t) + f»'(t) right)cdot2a^2=0.
end{equation*}
begin{equation*}
f'(t)=-f»'(t) quad Rightarrow quad f(t)=c_1+c_2,mbox{sin}t+c_3,mbox{cos}t.
end{equation*}
?
Как найти уравнение плоскости, в которой лежит кривая?
Известно, что плоская кривая лежит в своей соприкасающейся плоскости!
Второй способ — составить уравнение плоскости по трем точкам.
Как найти вектор кривизны
Рассмотрим плоскую кривую, заданную уравнением (y = fleft( x right).) Пусть в точке (Mleft( right)) проведена касательная к данной кривой, которая образует угол (alpha) с осью абсцисс (рисунок (1)). При смещении (Delta s) вдоль дуги кривой точка (M) переходит в точку (.) При этом положение касательной также изменяется: угол наклона касательной к оси (Ox) в точке () будет составлять (alpha + Deltaalpha.) Таким образом, при смещении точки кривой на расстояние (Delta s) касательная поворачивается на угол (Deltaalpha.) (Будем считать, что угол (alpha) возрастает при вращении против часовой стрелки.)
Абсолютное значение отношения (largefrac<<Delta alpha >><<Delta s>>normalsize) называется средней кривизной дуги (M.) В пределе, при (Delta s to 0,) мы получаем кривизну кривой в точке (M:) [K = limlimits_ <Delta s to 0>left| <frac<<Delta alpha >><<Delta s>>> right|.] Из приведенного определения следует, что кривизна в какой-либо точке кривой характеризует скорость вращения касательной в этой точке.
Для плоской кривой (y = fleft( x right)) кривизна в точке (Mleft( right)) выражается через первую и вторую производные функции (fleft( x right)) по формуле [K = frac <<left| right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] Если кривая задана в параметрической форме уравнениями (x = xleft( t right),) (y = yleft( t right),) то ее кривизна в произвольной точке (Mleft( right)) равна [K = frac <<left| right|>> <<<<left[ <<<left( right)>^2> + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] В случае, если кривая задана полярным уравнением (r = rleft( theta right),) кривизна находится по формуле [K = frac <<left| <+ 2 <<left( right)>^2> — rr»> right|>> <<<<left[ <+ <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] Радиусом кривизны кривой в точке (Mleft( right)) называется величина, обратная кривизне (K) данной кривой в рассматриваемой точке: [R = frac<1>.] Следовательно, для плоских кривых, заданных явным уравнением (y = fleft( x right),) радиус кривизны в точке (Mleft( right)) будет определяться выражением [R = frac <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>> <<left| right|>>.]
Очевидно, достаточно найти кривизну эллипса в точках (Aleft( right)) и (Bleft( <0,b>right)) (рисунок (2)), поскольку в силу симметрии кривой кривизна в двух противоположных вершинах эллипса будет такой же.
Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме : [x = acos t,;;;y = bsin t.] где (t) − параметр. В точке (Aleft( right)) параметр имеет значение (t = 0,) а в точке (Bleft( <0,b>right)) его значение равно (t = largefrac<pi ><2>normalsize.)
Данная функция достигает максимума в точках (x = largefrac<<2pi n>>normalsize,;n in Z.) В силу периодичности кривизна во всех точках максимума одинакова, поэтому достаточно рассмотреть лишь точку (x = 0).
В данном случае точка (x = 0) является точкой перегиба функции (y = arctan x.) Поскольку в точке перегиба вторая производная равна нулю, то кривизна здесь также должна быть равна нулю, что и показывает полученное решение.
Экспоненциальная функция (y = ) − это единственная уникальная функция, у которой производные любого порядка равны самой функции. Поэтому для кривизны данной кривой можно сразу написать следующую формулу: [ right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>> > = <frac<<>><<<<left( <1 + >> right)>^<largefrac<3><2>normalsize>>>>.> ] Знак модуля в числителе опущен, поскольку экспоненциальная функция всегда положительна.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Кривизна и кручение. Натуральные уравнения кривой
Краткие теоретические сведения
Кривизна кривой
Кривизной $k$ кривой в данной точке называют модуль скорости вращения касательной по отношению к длине дуги.
Регулярная дважды дифференцируемая без особых точек кривая $gamma$, заданная векторной функцией $vec=vec(t)$, имеет в каждой точке определенную кривизну, причем $$ |k(t)|=frac<|vec(t)times vec(t)|><|vec|^3>. $$
Для кривой, заданной параметрически $$ x=x(t), ,, y=y(t), ,, z=z(t), $$ кривизна в точке $P(t=t_0)$ находится по формуле: $$ k^2(t_0)=frac<left| begin y’ & z’ \ y»& z» \ end right|^2+left| begin z’ & x’ \ z»& x» \ end right|^2+left| begin x’ & y’ \ x» & y» \ end right|^2><Bigl((x’)^2+(y’)^2+(z’)^2Bigr)^3>, $$ где все производные вычисляются при $t=t_0$.
Если кривая задана естественной параметризацией $vec=vec(s)$, то векторы $vec(s)$ и $vec(s)$ перпендикулярны, причем $|vec(s)|=1$. Тогда выражение для кривизны принимает вид: $$ k(s)= |vec(s)|. $$
Что вы скажете о кривой, которая в каждой свой точке имеет нулевую кривизну?
Кручение
Абсолютным кручением $varkappa$ кривой называют скорость вращения соприкасающейся плоскости вокруг касательной. $$ |varkappa (t)|=frac<|(vec(t), vec(t), vec(t))|><|vec(t)times vec(t)|^2>. $$
В случае естественной параметризации $$ |varkappa(s)|=frac<|(vec(s), vec(s), vec(s))|> $$
Натуральные уравнения кривой
Если кривая задана естественной параметризацией $vec=vec(s)$, то кривизна и кручение будут являться функциями длины дуги $$ k=k(s), quad varkappa=varkappa(s). $$ Система этих двух соотношений называется натуральными уравнениями кривой.
Натуральные уравнения полностью определяют форму кривой, ибо связывают инварианты, которые не меняются при преобразовании координат (при изменении положения указанной кривой в пространстве относительно системы координат).
Решение задач
Задача 1 (Феденко №351)
Найдите кривизну кривой: $$ x=a,mbox^3t,,,y=a,mbox^3t. $$
Задача 2 (Феденко №380)
Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=mboxx$ в точке $A(pi/2,1)$ общие касательную и кривизну.
Задача 3 (Феденко №405)
Составьте натуральные уравнения кривой: $$ x=a(mbox,t+t,mbox,t), ,, y=a(mbox,t-t,mbox,t). $$
Краткое решение задачи 3
Натуральные уравнения: $$ k=frac<1>,,,s=frac <2>$$ или $$ k^2=frac<1><2as>. $$
Феденко записывает ответы через радиус кривизны: $R=frac<1>$.
Задача 4 (Феденко №486, №514)
Найдите кривизну и кручение, составьте натуральные уравнения кривой: $$ x=a,mboxt, , y=a,mboxt, , z=a, t. $$
Решение задачи 4
Задачу можно решать двумя способами:
1 способ. Найти $k(t), varkappa(t), s(t)$.
2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $vec=vec(s)$. А далее найти $k(s)$ и $varkappa(s)$.
В задаче №473 была та же кривая и мы получили, что $$s=asqrt<2>,mbox,t.$$ Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения: begin s=asqrt<2>,mboxt=asqrt<2>,sqrt<mbox^2t-1> ,, Rightarrow ,, mbox^2t=frac<2a^2>+1 ,, Rightarrow end begin k(s)=varkappa(s)=frac<1><2a,mbox^2t> = frac. end
Вычисления сделаны для $a>0$.
Задача 5 (Феденко №496)
Найдите функцию $f(t)$, для которой данная кривая — плоская: $$ vec(t)=t, , a,mboxt, , f(t)> $$
Решение задачи 5
Для плоской кривой кручение равно нулю: begin varkappa(t) = left| begin -a,mboxt & a,mboxt & f'(t) \ -a,mboxt & -a,mboxt & f»(t) \ a,mboxt & -a,mboxt & f»'(t) \ end right| = left( f'(t) + f»'(t) right)cdot2a^2=0. end begin f'(t)=-f»'(t) quad Rightarrow quad f(t)=c_1+c_2,mboxt+c_3,mboxt. end
Как найти уравнение плоскости, в которой лежит кривая?
Известно, что плоская кривая лежит в своей соприкасающейся плоскости! Второй способ — составить уравнение плоскости по трем точкам.
Кривизна плоской кривой
Под кривизной линии понимают степень ее отклонения от прямой. Не давая пока точных определений, заметим, что чем больше радиус окружности, тем менее она искривлена, тем больше ее участок заданной длины напоминает отрезок прямой той же длины. При этом окружность одинаково искривлена во всех точках. В то же время парабола наиболее искривлена в ее вершине, а по мере удаления от вершины кривизна становится меньше.
Чтобы дать точное определение кривизны, рассмотрим гладкую дугу . Если бы эта дуга не была искривлена, т. е. если бы она была отрезком прямой линии, то касательные в начале и конце дуги имели бы одинаковое направление (совпадающее с направлением отрезка). Таким образом, за меру искривленности данной дуги в целом следует принять угол поворота касательной к этой дуге при движении от начала дуги к ее концу. Например, для полуокружности этот угол равен (рис. 55), для всей окружности он равен , а для дуги синусоиды, изображенной на рисунке 56, этот угол равен нулю, так как при обходе дуги касательная возвращается в исходное положение, не сделав при этом полного оборота.
Угол поворота касательной считают положительным, если вращение происходит против часовой стрелки, и отрицательным в противном случае.
Однако угол поворота касательной показывает лишь полную искривленность линии. Поэтому полуокружности малого и большого радиусов дают один и тот же угол поворота , в то время как искривленность большой окружности в каждой точке меньше, чем малой. Это показывает, что нам надо учитывать не только угол поворота , но и длину дуги, на протяжении которой получился этот поворот касательной. Иными словами, следует рассчитывать угол поворота на единицу длины дуги, или, иначе, отношение величины этого угла к длине дуги. Назовем это отношение средней кривизной данной дуги:
Например, длина полуокружности радиуса равна , а соответствующий ей угол поворота равен . Значит, средняя кривизна полуокружности равна
т. е. обратно пропорциональна радиусу. Очевидно, что тот же результат получился бы, если бы мы взяли любую другую дугу окружности радиуса .
Мы уже говорили, что, вообще говоря, кривизна данной линии различна в разных точках. Поэтому надо перейти от средней кривизны дуги к ее кривизне в данной точке. Введем следующее определение:
Определение. Кривизной дуги кривой в данной точке называется предел средней кривизны дуги , когда длина этой дуги стремится к нулю:
(разумеется, если этот предел не существует, то кривизна линии в данной точке не определена).
Перейдем к выводу расчетной формулы для кривизны. Выберем декартову систему координат (рис. 57). Из рисунка видно, что угол между касательными в точках и равен разности углов и , т. е. углов наклона касательных в этих точках к оси абсцисс. Это можно записать следующим образом: , где — угол наклона касательной к оси абсцисс. Поэтому формулу для кривизны можно переписать так:
Мы доказали, что кривизна дуги кривой является производной угла наклона касательной к положительному направлению оси абсцисс по длине дуги.
Пусть кривая задана уравнением на отрезке , где функция дважды дифференцируема. Тогда эта кривая спрямляема и имеет касательную в любой точке. При этом , а так как , то , и потому
Пример 1. Найти кривизну гиперболы в точке .
Решение. Воспользуемся формулой (2) кривизны кривой. Имеем:
Вычислить значения производных в данной точке . Таким образом,
Пример 2. Найти наибольшую кривизну линии кубической параболы .
Решение. Мы имеем: .
Чтобы найти наибольшее значение кривизны, вычислим
Приравнивая производную нулю, получаем: . В этой точке . Отметим, что при имеем , а при будет . Поэтому вдоль кривой кривизна плавно возрастает от нуля до , а потом плавно убывает.
Это используется при строительстве железных дорог для построения переходных кривых, вдоль которых кривизна плавно возрастает от нуля до требуемого значения.
http://vmath.ru/vf5/diffgeom/seminar3
http://mathhelpplanet.com/static.php?p=krivizna-ploskoi-krivoi