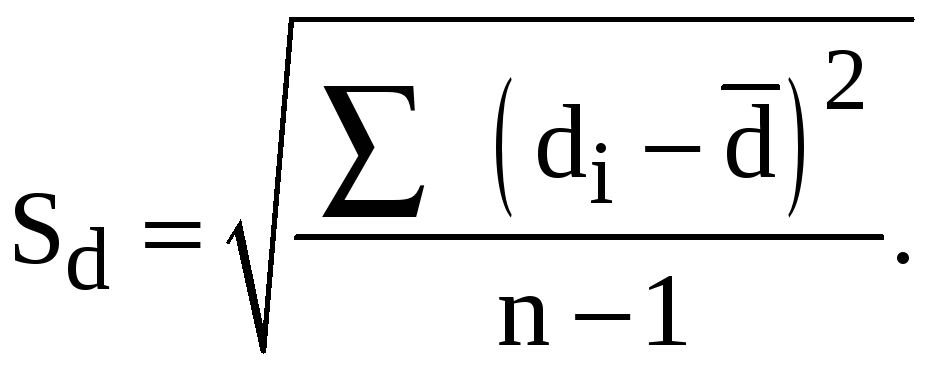-Критерий Стьюдента
Назначение
критерия.
Критерий предназначен для оценки
различий между двумя
параметрическими эмпирическими
распределениями по среднему значению
(уровню)
какого-либо признака, количественно
измеренного. Он позволяет выявлять
различия между выборками, когда
.
Описание
критерия.
Эмпирическое расчетное значение
критерия
отражает, насколько велика зона
совпадения между рядами. Чем больше
,
тем более
вероятно,
что различия достоверны.
Гипотезы
Уровень признака
в группе
2 не ниже
уровня признака в группе
1.
Уровень признака
в группе
2 ниже
уровня признака в группе
1.
Алгоритм расчета t-критерия Стьюдента для независимых выборок измерений
1.
Определить расчетное значение
-критерия
по формуле
(1)
где
степень свободы, которая определяется
как
2.
Определить критическое значение
-критерия
(см. прил., табл. А3)
при заданном
уровне значимости и степени свободы.
3.
Сравнить расчетное и критическое
значения
-критерия.
Если расчетное значение больше или
равно критическому, то гипотеза равенства
средних значений в двух выборках
измерений отвергается
.
Во всех других случаях она принимается
на заданном уровне значимости.
Пример.
Две группы студентов обучались по двум
различным методикам. В конце обучения
с ними был проведен тест по всему курсу.
Необходимо оценить, насколько существенны
различия в полученных знаниях. Результаты
тестирования представлены в таблице
1.
Таблица
1
Рассчитаем
выборочное среднее, дисперсию и
стандартное отклонение:
Определим по
формуле
(1)
значение
По таблице
(см. прил.,
табл. А3) находим критическое значение
для уровня значимости
Вывод:
так как
расчетное значение критерия меньше
критического
,
гипотеза
подтверждается и существенных различий
в методиках обучения нет на уровне
значимости
0,01.
Алгоритм расчета -критерия Стьюдента для зависимых выборок измерений
-
Определить
расчетное значение
-критерия
по формуле
где
,
6.
Рассчитать степень свободы
7.
Определить критическое значение
-критерия
(см. прил., табл. А3).
8.
Сравнить расчетное и критическое
значение
-критерия.
Если расчетное значение больше или
равно критическому, то гипотеза равенства
средних значений в двух выборках
изменений отвергается
Во всех других случаях она принимается
на заданном уровне значимости.
-Критерий Манна-Уитни
Назначение
критерия. Критерий
предназначен для оценки различии между
двумя
непараметрическими выборками по
уровню
какого-либо
признака, количественно измеренного.
Он позволяет выявлять различия между
малыми
выборками,
когда
Описание
критерия
Этот метод
определяет, достаточно ли мала зона
пересекающихся значений между двумя
рядами. Чем меньше эта область, тем более
вероятно, что различия достоверны.
Эмпирическое значение критерия и
отражает то, насколько велика зона
совпадения между рядами. Поэтому, чем
меньше
тем
более
вероятно, что различия достоверны.
Гипотезы
Уровень
признака в группе
2 не ниже
уровня признака в группе
1.
Уровень признака
в группе
2 ниже
уровня признака в группе
1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах. Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2. Проверить распределения на нормальность.
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.
17 авг. 2022 г.
читать 2 мин
Всякий раз, когда вы проводите t-тест, в результате вы получаете тестовую статистику. Чтобы определить, являются ли результаты t-теста статистически значимыми, можно сравнить статистику теста с критическим значением T. Если абсолютное значение тестовой статистики больше критического значения Т, то результаты теста статистически значимы.
Критическое значение T можно найти с помощью таблицы распределения t или с помощью статистического программного обеспечения.
Чтобы найти критическое значение T, необходимо указать:
- Уровень значимости (обычно выбирают 0,01, 0,05 и 0,10).
- Степени свободы
- Тип теста (односторонний или двусторонний)
Используя эти три значения, вы можете определить критическое значение T для сравнения со статистикой теста.
Связанный: Как найти критическое значение Z в Excel
Как найти критическое значение T в Excel
Excel предлагает две функции для нахождения критического значения T.
Т.ОБР.
Чтобы найти критическое значение T в Excel для одностороннего теста , вы можете использовать функцию T.ОБР.() , которая использует следующий синтаксис:
T.INV (вероятность, град_свободы)
- вероятность: уровень значимости для использования
- deg_freedom : Степени свободы
Эта функция возвращает критическое значение из распределения t для одностороннего теста на основе уровня значимости и предоставленных степеней свободы.
Т.ОБР.2Т
Чтобы найти критическое значение T в Excel для двустороннего теста , вы можете использовать функцию T.ОБР.2T() , которая использует следующий синтаксис:
T.INV.2T (вероятность, град_свободы)
- вероятность: уровень значимости для использования
- deg_freedom : Степени свободы
Эта функция возвращает критическое значение из распределения t для двустороннего теста на основе уровня значимости и предоставленных степеней свободы.
Примеры поиска критического значения T в Excel
В следующих примерах показано, как найти критическое значение T для левостороннего, правостороннего и двустороннего критериев.
Левосторонний тест
Чтобы найти критическое значение T для левостороннего критерия с уровнем значимости 0,05 и степенями свободы = 11, мы можем ввести в Excel следующую формулу: T.ОБР(0,05, 11)
Это возвращает значение -1,79588.Это критическое значение для левостороннего теста с уровнем значимости 0,05 и степенями свободы = 11.
Правосторонний тест
Чтобы найти критическое значение T для правостороннего критерия с уровнем значимости 0,05 и степенями свободы = 11, мы можем ввести в Excel следующую формулу: ABS( T.ОБР(0,05, 11))
Это возвращает значение 1,79588.Это критическое значение для двустороннего теста с уровнем значимости 0,05 и степенями свободы = 11.
Двусторонний тест
Чтобы найти критическое значение T для двустороннего критерия с уровнем значимости 0,05 и степенями свободы = 11, мы можем ввести в Excel следующую формулу: T.ОБР.2T(0,05, 11)
Это возвращает значение 2.200985.Это критическое значение для двустороннего теста с уровнем значимости 0,05 и степенями свободы = 11.
Обратите внимание, что это также соответствует числу, которое мы нашли бы в таблице распределения t с α = 0,05 для двух хвостов и DF (степени свободы) = 11.
Предостережения по поиску критического значения T в Excel
Обратите внимание, что обе функции T.ОБР () и T.ОБР.2T() в Excel выдают ошибку, если происходит одно из следующих событий:
- Если какой-либо аргумент не является числовым.
- Если значение вероятности меньше нуля или больше 1.
- Если значение для deg_freedomменьше 1.
t-критерий Стьюдента – общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента.
Таблица значений критерия Стьюдента в теории вероятностей и математической статистике используется довольно часто. На сайте можно посмотреть примеры ее использования в следующих задачах:
-
Доверительные интервалы для среднего и дисперсии
-
Проверка гипотезы о равенстве средних
Ниже размещена таблица критический точек t-критерия Стьюдента для односторонней и двусторонней критической области.
|
Число степеней свободы k |
Уровень значимости α (двусторонняя критическая область) | |||||
| 0,1 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 | |
| 1 | 6,31 | 12,70 | 31,82 | 63,70 | 318,30 | 637,00 |
| 2 | 2,92 | 4,30 | 6,97 | 9,92 | 22,33 | 31,60 |
| 3 | 2,35 | 3,18 | 4,54 | 5,84 | 10,22 | 12,90 |
| 4 | 2,13 | 2,78 | 3,75 | 4,60 | 7,17 | 8,61 |
| 5 | 2,01 | 2,57 | 3,37 | 4,03 | 5,89 | 6,86 |
| 6 | 1,94 | 2,45 | 3,14 | 3,71 | 5,21 | 5,96 |
| 7 | 1,89 | 2,36 | 3,00 | 3,50 | 4,79 | 5,40 |
| 8 | 1,86 | 2,31 | 2,90 | 3,36 | 4,50 | 5,04 |
| 9 | 1,83 | 2,26 | 2,82 | 3,25 | 4,30 | 4,78 |
| 10 | 1,81 | 2,23 | 2,76 | 3,17 | 4,14 | 4,59 |
| 11 | 1,80 | 2,20 | 2,72 | 3,11 | 4,03 | 4,44 |
| 12 | 1,78 | 2,18 | 2,68 | 3,05 | 3,93 | 4,32 |
| 13 | 1,77 | 2,16 | 2,65 | 3,01 | 3,85 | 4,22 |
| 14 | 1,76 | 2,14 | 2,62 | 2,98 | 3,79 | 4,14 |
| 15 | 1,75 | 2,13 | 2,60 | 2,95 | 3,73 | 4,07 |
| 16 | 1,75 | 2,12 | 2,58 | 2,92 | 3,69 | 4,01 |
| 17 | 1,74 | 2,11 | 2,57 | 2,90 | 3,65 | 3,95 |
| 18 | 1,73 | 2,10 | 2,55 | 2,88 | 3,61 | 3,92 |
| 19 | 1,73 | 2,09 | 2,54 | 2,86 | 3,58 | 3,88 |
| 20 | 1,73 | 2,09 | 2,53 | 2,85 | 3,55 | 3,85 |
| 21 | 1,72 | 2,08 | 2,52 | 2,83 | 3,53 | 3,82 |
| 22 | 1,72 | 2,07 | 2,51 | 2,82 | 3,51 | 3,79 |
| 23 | 1,71 | 2,07 | 2,50 | 2,81 | 3,59 | 3,77 |
| 24 | 1,71 | 2,06 | 2,49 | 2,80 | 3,47 | 3,74 |
| 25 | 1,71 | 2,06 | 2,49 | 2,79 | 3,45 | 3,72 |
| 26 | 1,71 | 2,06 | 2,48 | 2,78 | 3,44 | 3,71 |
| 27 | 1,71 | 2,05 | 2,47 | 2,77 | 3,42 | 3,69 |
| 28 | 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 |
| 29 | 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 |
| 30 | 1,70 | 2,04 | 2,46 | 2,75 | 3,39 | 3,65 |
| 40 | 1,68 | 2,02 | 2,42 | 2,70 | 3,31 | 3,55 |
| 60 | 1,67 | 2,00 | 2,39 | 2,66 | 3,23 | 3,46 |
| 120 | 1,66 | 1,98 | 2,36 | 2,62 | 3,17 | 3,37 |
| ∞ | 1,64 | 1,96 | 2,33 | 2,58 | 3,09 | 3,29 |
|
Число степеней свободы k |
0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 |
| Уровень значимости α (односторонняя критическая область) |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример решения задачи
Задача
Имеется
три независимых реализации нормальной случайной величины: 0.8, 3.2, 2.0.
Построить
доверительный интервал для среднего.
Указание:
воспользоваться таблицами Стьюдента
Решение
Вычислим
среднее и
исправленную дисперсию:
Найдем
доверительный интервал для оценки неизвестного среднего.
Он считается по формуле:
По таблице распределения Стьюдента:
Искомый доверительный интервал для среднего: