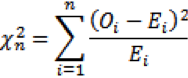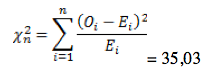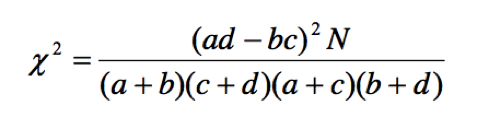До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.
Так был изобретен критерий χ2 (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.
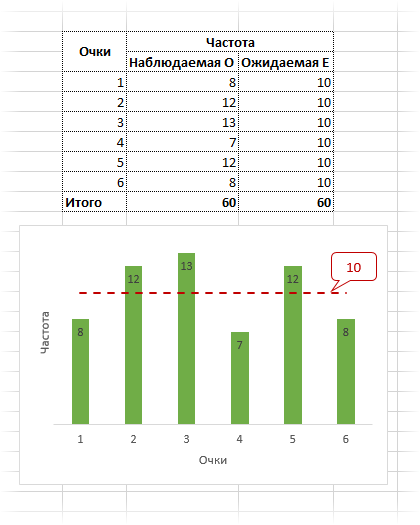
Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.
- Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
- Распределение этой меры при справедливости гипотезы о том, что различий нет.
Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.
Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной Ei будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение
имеет стандартное нормальное распределение.
Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.
У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.
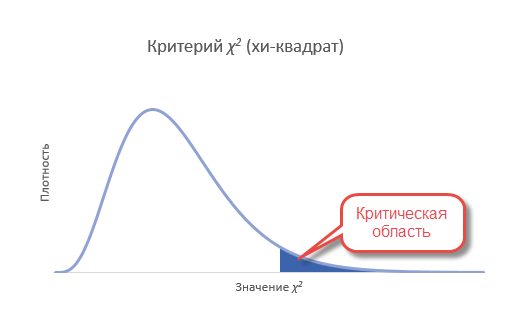
Это и есть статистика для критерия Хи-квадрат Пирсона. Если частоты действительно соответствуют ожидаемым, то значение статистики Хи-квадрат будет относительно не большим (отклонения находятся близко к нулю). Большое значение статистики свидетельствует в пользу существенных различий между частотами.
«Большой» статистика Хи-квадрат становится тогда, когда появление наблюдаемого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение статистики Хи-квадрат при многократном повторении эксперимента, когда гипотеза о согласии частот верна.
Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем больше слагаемых, тем больше ожидается значение статистики, ведь каждое слагаемое вносит свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ2 – это целое семейство распределений.
И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.
По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам Хи-квадрат).
Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.
Примерно также распределение статистики может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.
Таким образом, распределение хи квадрат (χ2) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. Формальное определение следующее. Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.
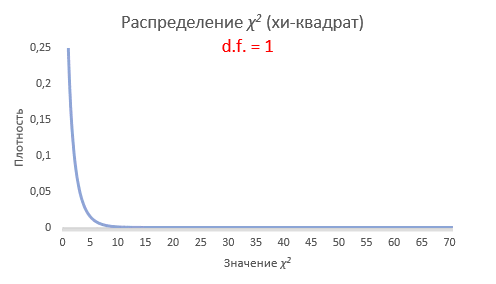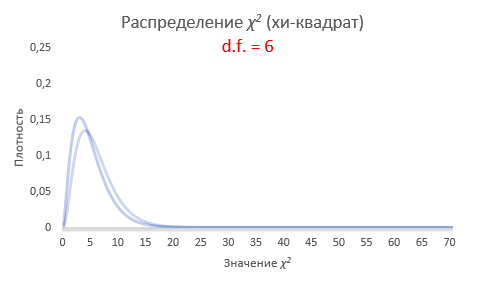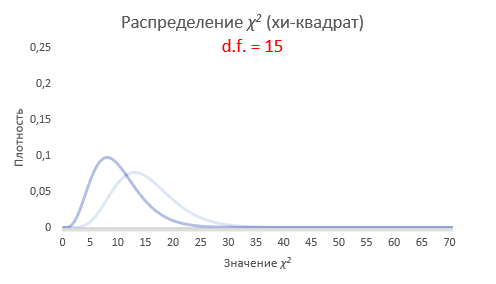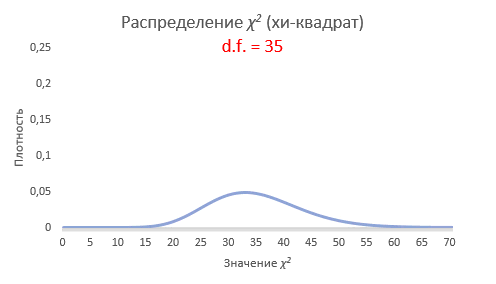
Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).
Проверка гипотезы по критерию Хи квадрат Пирсона
Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по статистике Хи-квадрат. Далее либо полученную статистику сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда статистика окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.
Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение статистики критерия хи-квадрат.
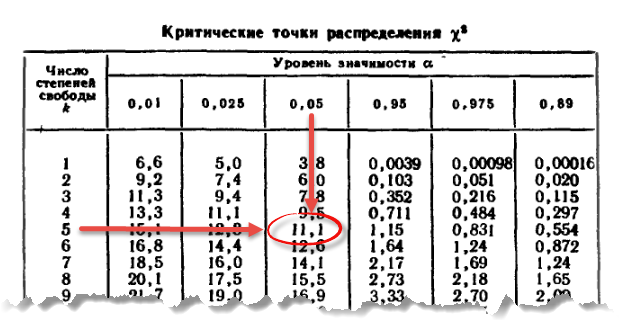
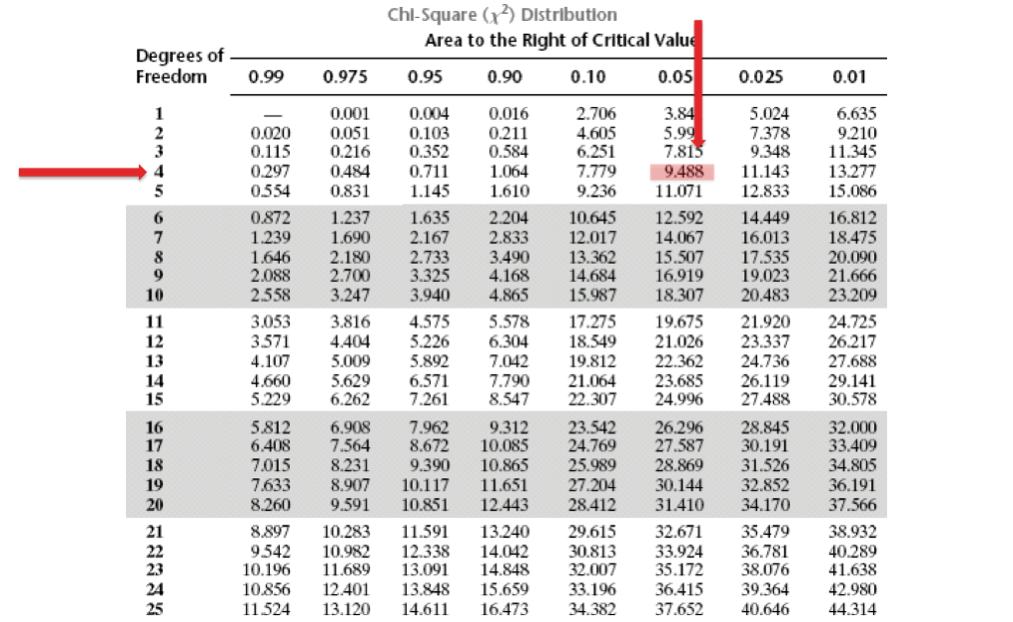
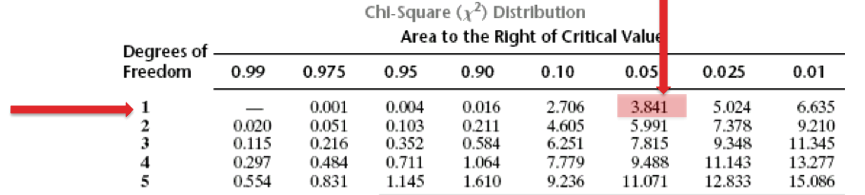
Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ20,05; 5 = 11,1.
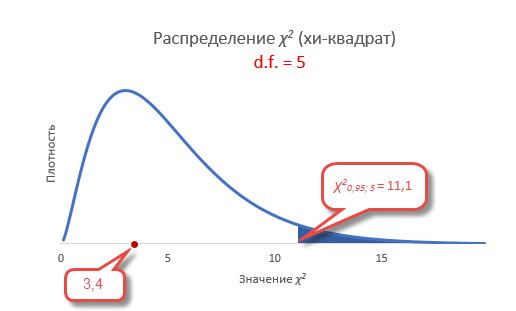
Сравним фактическое и табличное значение. 3,4 (χ2) < 11,1 (χ20,05; 5). Расчетный значение оказалось меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.
Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.
Ниже их краткое описание.
ХИ2.ОБР – критическое значение Хи-квадрат при заданной вероятности слева (как в статистических таблицах)
ХИ2.ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.
ХИ2.РАСП – p-value слева (можно рассчитать плотность).
ХИ2.РАСП.ПХ – p-value справа.
ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.
Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:
=ХИ2.ОБР(0,95;5)
Или так
=ХИ2.ОБР.ПХ(0,05;5)
Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).
Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ2 = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)
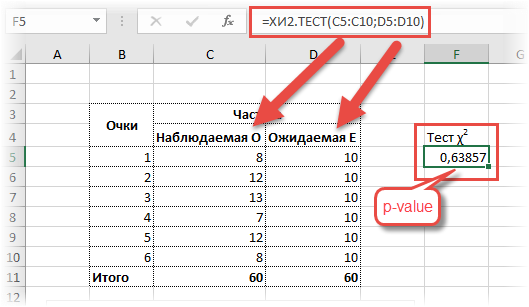
=ХИ2.РАСП.ПХ(3,4;5) = 0,63857
Значит, при 5-ти степенях свободы вероятность получить значение критерия χ2 = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.
А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.
Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.
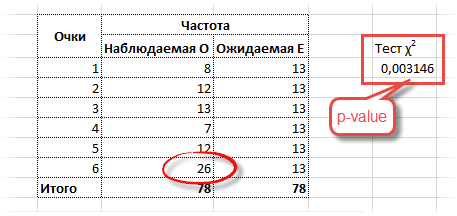
Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).
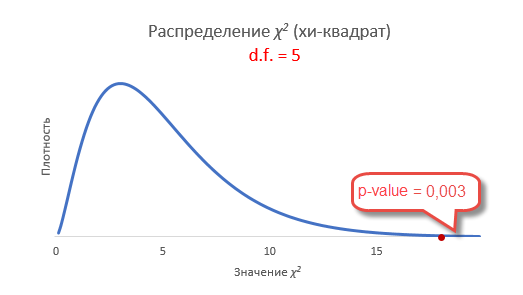
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.
Статистика критерия хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).
Надеюсь, мне удалось объяснить, что такое критерий согласия χ2 (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.
Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.
Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.
Скачать файл с примером.
Поделиться в социальных сетях:
17 авг. 2022 г.
читать 1 мин
Когда вы проводите тест Хи-квадрат, в результате вы получаете тестовую статистику. Чтобы определить, являются ли результаты теста хи-квадрат статистически значимыми, можно сравнить статистику теста с критическим значением хи-квадрат.Если статистика теста больше критического значения хи-квадрат, то результаты теста являются статистически значимыми.
Критическое значение хи-квадрат можно найти с помощью таблицы распределения хи-квадрат или с помощью статистического программного обеспечения.
Чтобы найти критическое значение хи-квадрат, вам нужно:
- Уровень значимости (обычно выбирают 0,01, 0,05 и 0,10).
- Степени свободы
Используя эти два значения, вы можете определить значение хи-квадрата, которое будет сравниваться со статистикой теста.
Как найти критическое значение хи-квадрат в Excel
Чтобы найти критическое значение хи-квадрат в Excel, вы можете использовать функцию ХИИЗВ.ОБР.ПВ() , которая использует следующий синтаксис:
CHISQ.INV.RT (вероятность, град_свободы)
- вероятность: уровень значимости для использования
- deg_freedom : Степени свободы
Эта функция возвращает критическое значение из распределения хи-квадрат на основе уровня значимости и предоставленных степеней свободы.
Например, предположим, что мы хотим найти критическое значение хи-квадрат для уровня значимости 0,05 и степеней свободы = 11.
В Excel мы можем ввести следующую формулу: CHISQ.ОБР.ВУ(0,05, 11)
Это возвращает значение 19,67514.Это критическое значение для уровня значимости 0,05 и степеней свободы = 11.
Обратите внимание, что это также соответствует числу, которое мы нашли бы в таблице распределения хи-квадрата с α = 0,05, DF (степени свободы) = 11.
Предостережения по поиску критического значения хи-квадрат в Excel
Обратите внимание, что функция ХИ.ОБР.ПВ() в Excel выдаст ошибку, если произойдет одно из следующих событий:
- Если какой-либо аргумент не является числовым.
- Если значение вероятности меньше нуля или больше 1.
- Если значение для deg_freedomменьше 1.
Ниже представлена таблица значений критических точек распределения χ2 (хи-квадрат) критерия Пирсона, широко используемые в задачах математической статистики, таких как построение доверительных интервалов,
проверка статистических гипотез и непараметрическое оценивание.
|
Число степеней свободы k |
Уровень значимости α | |||||
| 0,01 | 0,025 | 0,05 | 0,95 | 0,975 | 0,99 | |
| 1 | 6,6 | 5 | 3,8 | 0,0039 | 0,00098 | 0,00016 |
| 2 | 9,2 | 7,4 | 6 | 0,103 | 0,051 | 0,02 |
| 3 | 11,3 | 9,4 | 7,8 | 0,352 | 0,216 | 0,115 |
| 4 | 13,3 | 11,1 | 9,5 | 0,711 | 0,484 | 0,297 |
| 5 | 15,1 | 12,8 | 11,1 | 1,15 | 0,831 | 0,554 |
| 6 | 16,8 | 14,4 | 12,6 | 1,64 | 1,24 | 0,872 |
| 7 | 18,5 | 16 | 14,1 | 2,17 | 1,69 | 1,24 |
| 8 | 20,1 | 17,5 | 15,5 | 2,73 | 2,18 | 1,65 |
| 9 | 21,7 | 19 | 16,9 | 3,33 | 2,7 | 2,09 |
| 10 | 23,2 | 20,5 | 18,3 | 3,94 | 3,25 | 2,56 |
| 11 | 24,7 | 21,9 | 19,7 | 4,57 | 3,82 | 3,05 |
| 12 | 26,2 | 23,3 | 21 ,0 | 5,23 | 4,4 | 3,57 |
| 13 | 27,7 | 24,7 | 22,4 | 5,89 | 5,01 | 4,11 |
| 14 | 29,1 | 26,1 | 23,7 | 6,57 | 5,63 | 4,66 |
| 15 | 30,6 | 27,5 | 25 | 7,26 | 6,26 | 5,23 |
| 16 | 32 | 28,8 | 26,3 | 7,96 | 6,91 | 5,81 |
| 17 | 33,4 | 30,2 | 27,6 | 8,67 | 7,56 | 6,41 |
| 18 | 34,8 | 31,5 | 28,9 | 9,39 | 8,23 | 7,01 |
| 19 | 36,2 | 32,9 | 30,1 | 10,1 | 8,91 | 7,63 |
| 20 | 37,6 | 34,2 | 31,4 | 10,9 | 9,59 | 8,26 |
| 21 | 38,9 | 35,5 | 32,7 | 11,6 | 10,3 | 8,9 |
| 22 | 40,3 | 36,8 | 33,9 | 12,3 | 11 | 9,54 |
| 23 | 41,6 | 38,1 | 35,2 | 13,1 | 11,7 | 10,2 |
| 24 | 43 | 39,4 | 36,4 | 13,8 | 12,4 | 10,9 |
| 25 | 44,3 | 40,6 | 37,7 | 14,6 | 13,1 | 11,5 |
| 26 | 45,6 | 41,9 | 38,9 | 15,4 | 13,8 | 12,2 |
| 27 | 47 | 43,2 | 40,1 | 16,2 | 14,6 | 12,9 |
| 28 | 48,3 | 44,5 | 41,3 | 16,9 | 15,3 | 13,6 |
| 29 | 49,6 | 45,7 | 42,6 | 17,7 | 16 | 14,3 |
| 30 | 50,9 | 47 | 43,8 | 18,5 | 16,8 | 15 |
Пример решения задачи
Задача
Имеется
три независимых реализации нормальной случайной величины: 0.6, 3.4, 2.0.
Проверить
гипотезу
: дисперсия равна
10.0.
Используются
таблицы распределения хи-квадрат.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Вычислим
среднее и
исправленную дисперсию:
Для
того, чтобы при заданном уровне значимости
проверить нулевую гипотезу
о равенстве неизвестной генеральной дисперсии
гипотетическому значению
при конкурирующей гипотезе
вычисляем наблюдаемое значение критерия:
При
уровне значимости
находим:
— нет
оснований отвергнуть нулевую гипотезу
In this article, we are going to see how to find the Chi-Square Critical Value in R programming language.
When the Chi-Square test is conducted, we get test statistics as an outcome. In order to find out whether the results of the Chi-Square are statistically significant, the test statistic is compared with the Chi-Square critical value. If the outcome of the test-statistic comes out to be greater than the Chi-Square statistic, the results of the test are considered statistically significant.
In order to Chi-Square critical value, we need the following data beforehand:
- A significance level
- Degrees of freedom
Determining Chi-Square critical value in R
In order to determine Chi-Square critical value, R provides us qchisq() function that has the following syntax:
Syntax: qchisq(p, df, lower.tail=TRUE)
Parameters:
- p: The significance level to use
- df: The degrees of freedom
- lower.tail = TRUE: Then the probability to the left of p in the F distribution is returned
- lower.tail = FALSE: Then the probability to the right is returned.
- Note that by default is TRUE.
Return Type: Returns the critical-value from the Critical-Square distribution
Let us consider an example in which we need to determine the Chi-Square critical value for the following data:
- df = 7
- significance level = 0.01
R
qchisq(p = .01, df = 7, lower.tail = FALSE)
Output:
Hence, the Chi-Square critical value for a significance level of 0.01 and degrees of freedom = 7 comes out to be equal to 18.475. Hence, if the Chi-Square test statistic comes out to be greater than 18.475 then the results of the test would be considered statistically significant.
Relation of alpha and chi-square statistic
Alpha and chi-square critical values are inversely proportional to each other. In other words, larger critical values lead to smaller alpha values. Let the significance level be 0.01 and the degree of freedom be 5. Now, let’s compute the Chi-Square critical value:
Example 1:
R
qchisq(p = .01, df = 5, lower.tail = FALSE)
Output:
Now let the significance level be having the same degree of freedom as taken in the previous example (that is 5) but the significance level taken is 0.05:
Example 2:
R
qchisq(p = .05, df = 5, lower.tail = FALSE)
Output:
As you can see in the output, by increasing the significance level from 0.01 to 0.05 the Chi-Square critical value decreased from 15.086 to 11.070.
Last Updated :
28 Mar, 2022
Like Article
Save Article
Хи-квадрат (χ2) Пирсона: условия применения метода и интерпретация
Хи-квадрат Пирсона один из самых популярных статистических критериев для анализа качественных данных (номинальных, порядковых, ранговых), анализа частот. Однако, как и у каждого статистического критерия у хи-квадрата есть свои собственные правила применения метода, его интерпретации. Для того, чтобы Вы могли успешно овладеть этим ценнейшим статистическим инструментом сравнения статистических совокупностей по качественным данным предлагаем Вам ознакомиться с этой учебной статьей.
Правила использования хи-квадрата Пирсона
Условия применения хи-квадрата Пирсона
Как рассчитывать хи-квадрат Пирсона
Учет степеней свободы при применении хи-квадрата Пирсона
Пример корректной интерпретации хи-квадрата Пирсона
Как использовать хи-квадрат Пирсона?
Хи-квадрат используется прежде всего для анализа таблиц сопряженности (вид таблицы, которая учитывает совместное влияние фактора на исход, данные в таблице сопряженности должны быть представлены в виде частоты номинальных данных или интервалами, но не непрерывными количественными величинами). Стоит отметить, что при работе с сопряженными таблицами хи-квадрат часто является поддержкой для анализа влияния факторов риска с помощью расчета рисков (абсолютный и относительный риски) и отношение шансов.
Таблицы сопряженности могут принимать различные формы, простейшая таблица сопряженности выглядит следующим образом:
| Исход есть | Исхода нет | Всего | |
| Фактор риска есть | A | B | A+B |
| Фактора риска нет | C | D | C+D |
| Всего | A+C | B+D | A+B+C+D |
Как заполнить таблицу сопряженности? Обратимся к простому примеру:
Например, Вы хотите с помощью таблицы сопряженности и как следствия хи-квадрата Пирсона выяснить есть ли различия в частоте артериальной гипертонии в группах курящего и некурящего населения. Предполагается, что по остальным параметрам Ваши группы равномерны и превалирующим фактором риска развития артериальной гипертензии будет именно курение.
Для проведения исследования на основании ретроспективных данных (дизайн: случай-контроль) были отобраны две группы исследуемых — в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую группу вошли 80 некурящих такого же возраста, пола, и социального уровня (прочие систематически ошибки случайны).
В первой группе у 40 человек отмечалась артериальная гипертензия. Во второй — у 32 человек. Соответственно, референсное (нормальное) артериальное давление в группе «курильщиков» наблюдалось у 30 человек (70 — 40 = 30), а в группе «некурящих» нормальное АД наблюдалось у 48 (80 — 32 = 48).
Имея эти данные мы можем заполнить простейшую таблицу сопряженности:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
АД- артериальное давление
Как видно из таблицы: каждая строка соответствует группе пациентов, которая подвергается влиянию фактора, каждый столбец, в свою очередь, обозначает частоту исходов в группе (к примеру: произошло/ не произошло, как в нашем примере).
Таблицы сопряженности служат удобным средством визуализации комбинации частот «фактор- исход» и субстратом для расчета хи-квадрата Пирсона, который в нашем случае сможет дать статистически точный ответ о случайности или не случайности наших находок.
Условия применения статистического критерия хи-квадрата Пирсона
- Тип данных: параметры должны быть качественными цельночисленными частотами, измеренными в номинальной шкале (Например, тип диагноза)
бинарными (пол: мужской/женский, наличие или отсутствие заболевания)
порядковыми (степень артериальной гипертензии),
- Желательно, чтобы общее количество наблюдений было более 20,
- Ожидаемая частота, соответствующая нулевой гипотезе должна быть более 5, если ожидаемое явление принимает значение менее 5, то необходимо использовать точный Критерий Фишера.
- Для четырехпольных таблиц (2х2): Если ожидаемое значение принимает значение менее 10 (а именно 5<x<10), необходим расчет поправки Йетса таблиц сопряженности
- Сравниваемые частоты должны быть примерно одного размера
- Сопоставляемые группы должны быть независимыми (то есть единицы наблюдения в них разные, в отличие от связанных групп, анализирующих изменения «до-после» у одних и тех единиц наблюдений до и после вмешательства. Для таких ситуаций существует отдельный тест МакНемара (McNemar)
Запрещается: использовать хи-квадрат для анализа непрерывных абсолютных данных, процентов и долей
Как рассчитать критерий хи-квадрат Пирсона?
Для оценки достоверности различий по методу хи-квадрата Пирсона (критерий соответствия, коэффициент согласия) анализируется различия между реальной существующими частотами в группах (Observed) и рассчитываемыми по формуле ожидаемыми «гипотетическими» частотами, которые соответствуют распределению хи-квадрат. При малом различии ожидаемых и наблюдаемых частот (хи-квадрат не достиг своего критического значения) мы принимаем нулевую гипотезу об отсутствии различий. Если же различия оказываются существенными (критическое значение хи-квадрата достигаются для заданного числа степеней свободы) мы отвергаем нулевую гипотезу и говорим о наличии статистически значимых различий.
Чем больше теоретические числа, рассчитанные на основе Но-гипотезы, будут отличаться от фактических, тем более «хи -квадрат» будет отличаться от 0, тем с большей вероятностью можно отклонить Но-гипотезу и говорить о статистической достоверности имеющихся различий в сравниваемых совокупностях.
Основная формула для расчета хи-квадрата Пирсона:
Зачем учитывать количество степеней свободы при расчете хи-квадрата?
Для того, чтобы не утомлять читателя пространными разъяснениями «о сумме квадратом нормально распределенных случайных величин» скажем лишь, что оценка критического значения хи-квадрата зависит от степени свободы изменения частот, что это значит на практике для пользователя хи-квадрата? То, что чем более многопольная таблица перед Вами, тем больше степеней свободы, чем она меньше, тем меньше. Формула расчета хи-квадрата следующая:
Degree of freedom (d.f.) = (c-1)(r-1)
Column (c) – количество столбцов частотами, r- количество строк с частотами.
Таким образом, количество степеней свободы для стандартной 2х2 таблицы сопряженности составит:
d.f. = (2-1)*(2-1)=1
и так далее.
Примеры расчета хи-квадрата Пирсона
Пример 1:
Необходимо определить наличие влияния предшествующей степени нарушения кровообращения на исход комиссуротомии (хирургическое разделение спаек при стенозе клапанного отверстия сердца). Пациенты поступали на комиссуротомию с различными исходными уровнями нарушения кровообращения. После комиссуротомии пациенты были выписаны с различными исходами операции.
Фактор: Степень нарушения кровообращения
Исход: Результативность операции
Таблица: наблюдаемые (Observed) частоты распределения влияния степени нарушения кровообращения на результаты операции комиссуротомии
| Степень нарушения кровообращения | Всего больных | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 30 | 20 | 8 | 2 |
| III | 80 | 43 | 20 | 17 |
| IV | 60 | 10 | 40 | 10 |
| Всего | 170 | 73 | 68 | 29 |
| H0-гипотеза | 100% | 43% | 40% | 17% |
Первый этап
Расчет ожидаемых (Expected) величин (на основании групповых частот)
Второй этап
Сопоставление наблюдаемых и ожидаемых частот с нахождением их разницы (O-E)
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | +7 | -4 | -3 |
| III | +9 | -12 | +3 |
| IV | -16 | +16 | 0 |
| Всего | 0 | 0 | 0 |
Третий этап
Рассчитываем сумму отношений квадрата разности значений и делим ожидаемые данные (хи-квадрат) (O-E)2/E
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 49/13=3,77 | 16/12=1,33 | 9/5=1,80 |
| III | 81/34=2,38 | 144/32=4,50 | 9/14=0,64 |
| IV | 256/26=9,85 | 256/24=10,66 | 0/10*=0,10 |
| Всего | 16 | 16,49 | 2,54 |
как видно из данной таблицы одно из ожидаемых значений равно 0, в данном случае будет подставлена 1, корректнее применить точный критерий Фишера (см. Условия применения хи-квадрата Пирсона)
Четвертый этап
Необходимо соотнести полученное значение хи-квадрата с критическим значением хи-квадрата.Возникает вопрос, откуда брать критическое значение? Критическое значение хи-квадрата, как и для большинства, статистических критериев зависит от степени свободы и уровня достоверности (alpha), который Вы выбираете.В нашем случае, наше количество степеней свободы равно (3-1)*(3-1)=4, уровень значимости, который мы хотим соблюсти равен 0,05Обратимся к таблице критических значение хи-квадрата:
- Xи-квадрат (для d.f.=4 p=0.05) = 9.488
- Xи-квадрат (для d.f.=4 p=0.01) = 13.27735,03 > 13,277;
- p<0,01
Пример корректной интерпретации: Предшествующая степень нарушения кровообращения влияет на исход комиссуротомии (однако! Мы не можем говорить о направленности связи, то есть: улучшает-ухудшает сказать не можем), оптимально указать степень свободы, точное значение хи-квадрата, если есть возможность рассчитать точное значение достоверности, то так же стоит указать и его или остановиться на критическом значении достоверности (p<0,05 или p<0,01 и так далее).В нашем случае:d.f.=4, x2=35,03, p< 0.01
Пример 2: Вернемся к нашему примеру с влиянием курения на развитие артериальной гипертензии:Исходная четырехпольная таблица:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
Для четырехпольных таблиц существует упрощенная формула расчета значения хи-квадрата:
| Исход + | Исход 0 | Всего | |
| Фактор + | a | b | a+b |
| Фактор 0 | c | d | c+d |
| Всего | a+c | b+d | N |
- x2= (40х48 – 32х30)х150 / (70)(80)(72)(78) = (1920 – 960)2х150/31449600 = 138240000/31449600 = 4,395
- Сравним полученное значение хи-квадрата с критическим значением (для степени свободы 1, и уровнем значимости 3,841)
Правильная интерпретация: Курение оказывает влияние на формирование повышенного артериального давления df=1, x2= 4,395, p<0,05
Заключение по хи-квадрату Пирсона
хи-квадрат Пирсона является удобным статистическим методом для анализа изменения частот, оформленными в таблицы сопряженности для несвязанных групп. Как и все статистически инструменты хи-квадрат Пирсона имеет свои правила, преимущества и ограничения применения. Будьте внимательны и хи-квадрат Пирсона Вас не разочарует.
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях: