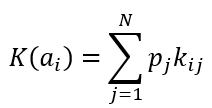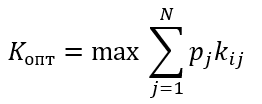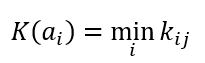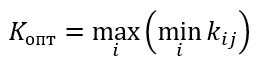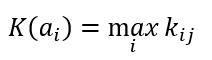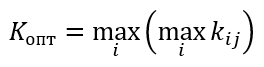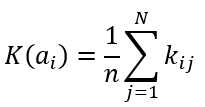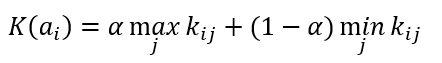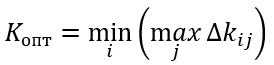Принятие решений по критери Вальда
В зависимости от того решается ли задача
на максимум или на минимум критерий
Вальда применяется в двух различных
вариантах:
-
Как maxmin-ный
критерий -
Как minimax-ный
критерий
Важнейшей особенностью этого критерия
является то, что он не требует знания
вероятности состояния природы.
Данный
критерий опирается на принцип наибольшей
осторожности, поскольку он основывается
на выборе наилучшей из всех наихудших
стратегий.
-
Если в исходной матрице по
условию задачи элменты этой матрицы
представляют собой потери лица,
принимающего решение, то при выборе
оптимальной стратегии используется
minimax-ный критерий.
Ri=>wi=minmax
Vij и читается: для
определения оптимальной стратегии Ri
необходимо в каждой строке матрицы Vij
найти максимальный элемент и из них
выбрать минимальный, который будет
соответствовать оптимальной стратегии. -
Если элементы исходной
матрицы составляют выигрыш лица
принимающего решение, то принимается
maxmin критерий решений:
Ri=>wi=maxminVij
И
рассчитывается: для определения
максимальной стратегии Ri
в каждой строке матрицы Vij находят
минимальный элемент, а потом из них
выбирают максимальный.
Пример тот же:
Vij=
|
Варианты возможности предприятия |
Вариант спроса и стоимости |
|||
|
1 |
2 |
3 |
4 |
|
|
R1 |
6 |
12 |
20 |
24 |
|
R2 |
9 |
7 |
9 |
28 |
|
R3 |
23 |
18 |
15 |
19 |
|
R4 |
27 |
24 |
21 |
15 |
По критерию: 24
28 и минимальная 23, значит лучшая стратегия
R3
23
27
Таким
образом для решения задачи при неполных
данных используя критерий Вальда в
качестве оптимальной выбирают стратегию
R3. Это и есть лучшая из
худших стратегий. Minmax
критерий называют критерием писсимиста.
Критерий Севиджа
Недостатком
критерия Вальда является его крайняя
писсимистичность. Эту писсимистичность
можно устранить, применяя для выбора
оптимальной стратегии критерий Севиджа.
Но надо помнить что критерий Севиджа в
качестве исходной использует не матрицу
проигрышей или выигрышей, а матрицу
рисков,
элементы которой рассчитываются из
выражений рис4.
Такая
запись означает, что разность Vij
и значением и является наилучшим.
Независимо
от того являются ли в исходной матрице
элементы Vij потерями или выигрышем в
обоих случаях элементы матрицы риска
дают величину потерь для лица принимающего
решение. Таким образом можно применять
к элементам матрицы риска только minmax
критерий. При этом критерий Севиджа
рекомендует в условиях неопределенности
выбирать ту стратегию Rj при которой
величина риска принимает наименьшее
значение в самой неблагоприятной
ситуации.
|
Варианты возможности предприятия |
Вариант спроса и стоимости |
||||
|
1 |
2 |
3 |
4 |
критерий |
|
|
1 |
0 |
5 |
11 |
9 |
11 |
|
2 |
3 |
0 |
0 |
13 |
13 |
|
3 |
17 |
11 |
6 |
4 |
17 |
|
4 |
21 |
17 |
12 |
0 |
21 |
Результатом
является R1, сравнивая с
критерием Вальда в котором был R3,
выбираем худший из лучших и называем
критерий крайнего оптимизма.
Можно полагать что правильное более
правильное решение будет располагаться
между критериями оптимизма и писсимизма.
Для вычисления промежуточного значения
и выбора оптимального заначения и
стратегии, которая позволит получить
результат между крайним оптимизмом и
писсимизмом необходимо ввести весовые
коэффициенты для решений. Эту задачу
решил Гурвиц.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основные критерии применяемые в процессе принятия решений в условиях неопределённости и риска, а также в игре с природой
Критерий среднего выигрыша
Формула критерия среднего выигрыша
Формула оптимального решения
Пример
Пусть даны вероятности, p1=0.2 p2=0.1 p3=0.3 p4=0.2, тогда получаем
K(a1)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.4=0.3
K(a2)=0.2*0.3+0.1*0.2+0.3*0.3+0.2*0.5=0.27
K(a3)=0.2*0.6+0.1*0.3+0.3*0.3+0.2*0.2=0.28
K(a4)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.3=0.25
Kопт=max{0.27; 0.48; 0.43; 0.51}=0.51
В итоги оптимальным вариантом выбора программы по критерию среднего выигрыша является вариант первой программы.
Критерий Вальда или пессимизма
Формула критерия Вальда или максимина
Формула оптимального решения по критерию Лапласа
Пример
K(a1)=min(0.4;0.5;0.3;0.4)=0.3
K(a2)=min(0.3;0.2;0.3;0.5)=0.2
K(a3)=min(0.6;0.3;0.3;0.2)=0.2
K(a4)=min(0.4;0.5;0.2;0.3)=0.2
Kопт=max{0.3; 0.2; 0.2; 0.2}=0.3
По критерию Вальда оптимальным решением является выбор первой программы.
Критерий максимакса или оптимизма
Формула критерия максимакса
Формула оптимального решения по критерию максимакса
Пример
K(a1)=max(0.4;0.5;0.3;0.4)=0.5
K(a2)= max (0.3;0.2;0.3;0.5)=0.5
K(a3)= max (0.6;0.3;0.3;0.2)=0.6
K(a4)= max (0.4;0.5;0.2;0.3)=0.5
Kопт=max{0.5; 0.5; 0.6; 0.5}=0.6
По критерию максимакса оптимальным решением является выбор третьей программы.
Критерий Лапласа
Формула критерия Лапласа
Формула оптимального решения по критерию Лапласа
Пример
Решение
K(a1)=0.25*(0.4+0.5+0.3+0.4)=0.4
K(a2)=0.25*(0.3+0.2+0.3+0.5)=0.325
K(a3)=0.25*(0.6+0.3+0.3+0.2)=0.35
K(a4)=0.25*(0.4+0.5+0.2+0.3)=0.35
Kопт=max{0.4; 0.325; 0.35; 0.35}=0.4
По критерию Лапласа оптимальным решением является выбор первой программы.
Критерий Гурвица
Пример
Формула критерия Гурвица
Формула оптимального решения по Гурвица критерию
Коэффициент α принимает значения от 0 до 1. Если α стремится к 1, то критерий Гурвица приближается к критерию Вальда, а при α стремящемуся к 0, то критерий Гурвица приближается к критерию максимакса.
Пусть α=0.7
K(a1)= 0.7* 0.5+(1-0.7)*0.3=0.44
K(a2)= 0.7* 0.5+(1-0.7)*0.2=0.41
K(a3)= 0.7* 0.6+(1-0.7)*0.2=0.48
K(a4)= 0.7* 0.5+(1-0.7)*0.2=0.41
Kопт=max{0.44; 0.41; 0.48; 0.41}=0.48
По критерию Гурвица оптимальным решением является выбор третьей программы.
Критерий Сэвиджа или минимакса (критерий потерь)
Формула критерия Сэвиджа для построения матрицы потерь
Формула для выбора максимального значения из матрицы потерь
Формула оптимального решения по критерию Сэвиджа
Для примера
Строим матрицу потерь по столбцам выбираем максимальное значение и поочередно вычитаем значения каждой ячейки соответствующего столбца согласно формуле, в итоге получим матрицу вида
K(a1)= max{0.2; 0; 0; 0.1}=0.2
K(a2)= max{0.3; 0.3; 0; 0}=0.3
K(a3)= max{0; 0.2; 0; 0.3}=0.3
K(a4)= max{0.2; 0; 0.1; 0.2}=0.2
Kопт=min{0.2; 0.3; 0.3; 0.2}=0.2
По критерию Сэвиджа оптимальным решением является выбор первой или четвёртой программы.
Таким образом, в соответствии со всеми приведёнными критериями большинство решений указывает на выбор первой программы.
Любую хозяйственную деятельность
человека можно рассматривать как игру с природой. В широком смысле под природой
будем понимать совокупность неопределенных факторов, влияющих на эффективность
принимаемых решений.
Управление любым объектом
осуществляется путем принятия последовательности управленческих решений. Для принятия решения
необходима информация (совокупность сведений о состоянии объекта управления и
условиях его работы). В тех случаях когда отсутствует
достаточно полная информация, возникает неопределенность в принятии решения. Причины этого могут быть
различны: требующаяся для полного обоснования решения информация принципиально
не может быть получена (неустранимая неопределенность); информация не может быть
получена своевременно, к моменту принятия решения; затраты, связанные с
получением информации, слишком высоки. По мере совершенствования средств сбора, передачи и обработки информации неопределенность
управленческих решении будет уменьшаться. К этому нужно стремиться.
Существование неустранимой неопределенности связано со случайным характером
многих явлений. Например, в торговле, случайный характер изменения спроса
делает невозможным его точное прогнозирование, a, следовательно, и формирование
идеально точного заказа на поставку товара. Принятие решения в этом случае
связано с риском. Приемка партии товара на основании выборочного контроля также
связана с риском принятия решения в условиях неопределенности. Неопределенность
может быть снята путем полного контроля всей партии, однако это может оказаться
слишком дорогостоящим мероприятием. В сельском хозяйстве, например, с целью
получения урожая человек предпринимает ряд действии (пашет землю, вносит
удобрения, борется с сорняками и т. п.). Окончательный результат (урожай)
зависит от действий не только человека, но и природы (дождь, засуха, вечер и т.
п.). Из приведенных примеров видно, что
полностью исключить неопределенность в управлении экономической системой
нельзя, хотя, повторим, к этому нужно стремиться. В каждом конкретном случае
следует принимать во внимание степень риска при принятии управленческих
решений, по возможности максимально учитывать имеющуюся информацию с целью
уменьшения неблагоприятных последствий, которые могут возникнуть из-за
ошибочных решений.
Две стороны, участвующие в игре,
будем называть игрок I и игрок II. Каждый из игроков располагает конечным
набором действий (чистых стратегий), которые он может применять в процессе
игры. Игра имеет повторяющийся,
циклический характер. о
каждом цикле игроки выбирают одну из своих стратегии, что однозначно определяет
платеж
. Интересы игроков
противоположны. Игрок I старается вести игру так, чтобы платежи были как можно
большими. Для игрока II желательны как можно меньшие значения платежей (с
учетом знака). Причем в каждом цикле выигрыш одного из игроков в точности
совпадает с проигрышем другого. Игры такого типа называются играми с нулевой
суммой.
Решить игру — значит определить
оптимальное поведение игроков. Решение игр является предметом теории игр.
Оптимальное поведение игрока инвариантно относительно изменения всех элементов
платежной матрицы на некоторую величину.
В общем случае определение оптимального
поведения игроков связано с решением двойственной пары задач линейного
программирования. В отдельных случаях могут быть использованы более простые
методы. Часто платежную матрицу удается упростить путем удаления из нее строк и
столбцов, соответствующих доминируемым стратегиям
игроков, доминируемой называется стратегия, все
платежи которой не лучше соответствующих платежей некоторой другой стратегии и
хотя бы один из платежей хуже соответствующего платежа этой другой стратегии,
называемой доминирующей.
В обычной стратегической игре
принимают участие «разумные и антагонистические» противники (противоборствующие
стороны). В таких играх каждая из сторон предпринимает именно те действия,
которые наиболее выгодны ей и менее выгодны противнику. Однако очень часто неопределенность, сопровождающая
некоторую операцию, не связана с сознательным противодействием противника, а
зависит от некой, не известной игроку I объективной действительности (природы).
Такого рода ситуации принято называть играми с природой. Игрок II — природа — в
теории статистических игр не является разумным игроком, так как рассматривается
как некая незаинтересованная инстанция, которая не выбирает для себя
оптимальных стратегий. Возможные состояния природы (ее стратегии) реализуются
случайным образом. В исследовании операций оперирующую сторону (игрока I) часто
называют статистиком, а сами операции — играми статистика с природой или
статистическими играми.
Рассмотрим игровую постановку
задачи принятия решения в условиях неопределенности. Пусть оперирующей стороне
необходимо выполнить операцию в недостаточно известной обстановке относительно
состояний которой можно сделать
предположений. Эти предположения
будем рассматривать как стратегии природы.
Оперирующая сторона в своем распоряжении имеет
возможных стратегий —
. Выигрыши игрока I
при каждой паре стратегий
и
— предполагаются известными и заданы платежной
матрицей
.
Задача заключается в определении
такой стратегии (чистой или смешанной), которая лри
ее применении обеспечила бы оперирующей стороне наибольший выигрыш.
Выше уже говорилось, что
хозяйственная деятельность человека может рассматриваться как игра с природой.
Основной особенностью природы как игрока является ее не заинтересованность в
выигрыше.
Анализ матрицы выигрышей игры с
природой начинается с выявления и отбрасывания
дублирующих и заведомо невыгодных стратегий лица, играющего с природой. Что
касается стратегий природы, то ни одну из них отбросить нельзя, так как каждое
из состояний природы может наступить случайным образом, независимо от действий
игрока I. Ввиду того что природа не противодействует
игроку I, может показаться, что игра с природой проще стратегической игры. На
самом деле это не так. Противоположность интересов игроков в стратегической
игре в некотором смысле как бы снимает неопределенность, чего нельзя сказать о
статистической игре. Оперирующей стороне в игре с природой легче в том
отношении, что она скорее .всего выиграет больше, чем
в игре против сознательного противника. Однако ей труднее принять обоснованное
решение, так как в игре с природой неопределенность ситуации сказывается в
гораздо более сильной степени.
После упрощения платежной матрицы
игры с природой целесообразно не только оценить выигрыш при той или иной
игровой ситуации, но и определить разность между максимально возможным
выигрышем при данном состоянии природы и выигрышем, который будет получен при
применении стратегии
в тех же условиях. Эта разность в теории игр
называется риском.
Природа меняет состояние
стихийно, совершенно не заботясь о результате игры. В антагонистической игре мы
предполагали, что игроки пользуются оптимальными (в определенном выше смысле)
смешанными стратегиями. Можно предположить, что природа применяет наверняка не
оптимальную стратегию. Тогда какую? Если бы существовал ответ на этот вопрос,
то принятие решения лицом, принимающим решения (ЛПР) сводилось бы к
детерминированной задаче.
Если вероятности
состояний
природы известны, то пользуются критерием
Байеса, в соответствии с которым оптимальной считается чистая стратегия
, при которой максимизируется
средний выигрыш:
Критерий Байеса предполагает, что
нам хотя и неизвестны условиях выполнения операций (состояния природы)
, но известны их вероятности
.
С помощью такого приема задача о
выборе решения в условиях неопределенности превращается в задачу о выборе
решения в условиях определенности, только принятое решение является оптимальным
не в каждом отдельном случае, а в среднем.
Если игроку
представляются в равной мере правдоподобными
все состояния
природы, то иногда полагают
и, учитывая, «принцип недостаточного
основания» Лапласа, оптимальной считают чистую стратегию
, обеспечивающую:
Если же смешанная стратегия
природы неизвестна, то в зависимости от гипотезы о поведении природы можно
предложить ряд подходов для обоснования выбора решения ЛПР. Свою оценку
характера поведения природы будем характеризовать числом
, которое можно связывать со
степенью активного «противодействия» природы как игрока Значение
соответствует наиболее пессимистичному
отношению ЛПР в смысле «содействия» природы в достижении им наилучших
хозяйственных результатов. Значение
соответствует наибольшему оптимизму ЛПР. Как
известно, в хозяйственной деятельности указанные крайности опасны. Скорее
всего, целесообразно исходить из некоторого промежуточного значения
. В этом случае используется
критерий Гурвица, согласно которому наилучшим решением ЛПР является чистая
стратегия
, соответствующая условию:
Критерий Гурвица (критерий
«оптимизма-пессимизма») позволяет руководствоваться при выборе рискового
решения в условиях неопределенности некоторым средним результатом
эффективности, находящимся в поле между значениями по критериям «максимакса» и «максимина» (поле между этими значениями
связано посредством выпуклой линейной функции).
В случае крайнего пессимизма ЛПР
указанный критерий называется критерием
Вальда. Согласно этому критерию, наилучшей считается максиминная
стратегия. Это критерий крайнего
пессимизма. По этому критерию ЛПР выбирает ту стратегию, которая гарантирует в
наихудших условиях максимальный выигрыш:
Такой выбор соответствует
наиболее робкому поведению ЛПР, когда он предполагает наиболее, неблагоприятное
поведение природы, боится больших потерь. Можно предположить, что он не получит
больших выигрышей. Согласно критерию Сэвиджа, следует
выбирать чистую стратегию
соответствующую условию:
где риск
.
Критерий Сэвиджа
(критерий потерь от «минимакса») предполагает, что из всех возможных вариантов
«матрицы решений» выбирается та альтернатива, которая минимизирует размеры
максимальных потерь по каждому из возможных решений. При использовании этого
критерия «матрица решения» преобразуется в «матрицу риска», в которой вместо
значений эффективности проставляются размеры потерь при различных вариантах
развития событий.
Недостатком критериев Вальда, Сэвиджа и Гурвица
является субъективная оценка поведения природы. Хотя указанные критерии и дают
некоторую логическую схему принятия решений, резонно все же задать вопрос: «А
почему сразу не выбрать субъективное решение, вместо того чтобы иметь дело с
разными критериями?» Несомненно, определение решения по различным критериям помогает
ЛПР оценить принимаемое решение с различных позиций и избежать грубых ошибок в
хозяйственной деятельности.
Задача
После
нескольких лет эксплуатации оборудование может оказаться в одном из трех
состояний:
-
требуется профилактический ремонт;
требуется замена отдельных деталей и узлов;
требуется капитальный ремонт.
В
зависимости от ситуации руководство предприятия может принять следующие
решения:
-
отремонтировать оборудование своими силами, что потребует затрат
;
вызвать специальную бригаду ремонтников, расходы в этом случае составят
;
заменить оборудование новым, реализовав устаревшее по остаточной стоимости.
Совокупные затраты на этот мероприятие составят
.
Требуется
найти оптимальное решение данной проблемы по критерию минимизации затрат с
учетом следующих предположений:
|
|
|
|
|
| a | 4 | 6 | 9 |
| b | 5 | 3 | 7 |
| c | 20 | 15 | 6 |
| q | 0.4 | 0.45 | 0.15 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Игра парная, статистическая. В игре участвуют
2 игрока: руководство предприятия и природа.
Под природой в данном случае понимаем
совокупность внешних факторов, которые определяют состояние оборудования.
Стратегия руководства:
—
отремонтировать оборудование своими силами
—
вызвать бригаду специалистов
—
заменить оборудование новым
Стратегия природы — 3 возможных состояния
оборудования.
— требуется профилактический ремонт;
— следует заменить отдельные детали и узлы;
— требуется капитальный ремонт.
Расчет платежной матрицы и матрицы рисков
Поскольку элементы матрицы — затраты,
то будем считать их выигрышными но со знаком минус. Платежная матрица:
|
|
|
|
|
|
|
|
-4 | -6 | -9 | -9 |
|
|
-5 | -3 | -7 | -7 |
|
|
-20 | -15 | -6 | -20 |
|
|
0.4 | 0.45 | 0.15 |
Составляем матрицу рисков:
|
|
|
|
|
|
|
|
(-4)-(-4)=0 | (-3)-(-6)=3 | (-6)-(-9)=3 | 3 |
|
|
(-4)-(-5)=1 | (-3)-(-3)=0 | (-6)-(-7)=1 | 1 |
|
|
(-4)-(-20)=16 | (-3)-(-15)=12 | (-6)-(-6)=0 | 16 |
Критерий Байеса
Определяем средние выигрыши:
По критерию Байеса оптимальной является стратегия
—
вызвать бригаду специалистов
Критерий Лапласа
Примем
Определим средние выигрыши:
По критерию Лапласа оптимальной является стратегия
— вызвать бригаду специалистов
Критерий Вальда
По критерию Вальда оптимальной является стратегия
— вызвать бригаду специалистов
Критерий Сэвиджа
По критерию Сэвиджа оптимальной
является стратегия
-вызвать
бригаду специалистов.
Критерий Гурвица
:
По критерию Гурвица оптимальной является стратегия
—
вызвать бригаду специалистов
Ответ: По всем критериям
оптимальной является стратегия «Вызвать бригаду специалистов».
Многие из нас не любят попадать в ситуацию, когда информации о внешних факторах очень мало, или она напрочь отсутствует, и при этом нужно срочно сделать важный выбор. Скорее всего, именно поэтому большинство людей предпочитает избегать на работе ответственности и довольствуется скромным, но вместе с тем относительно спокойным служебным положением. Если бы они знали о теории игр и о том, какую пользу могут сослужить критерии Вальда, Сэвиджа, Гурвица, карьера наиболее сообразительных из них наверняка бы стремительно пошла вверх.
Рассчитывай на худшее
Именно так можно охарактеризовать первый из перечисленных принципов. Критерий Вальда нередко называют еще критерием крайнего пессимизма или правилом минимального зла. В условиях ограниченных ресурсов и шаткого, неустойчивого положения вполне логичным представляется перестраховочная позиция, которая рассчитана на самый худший случай. Максиминный критерий Вальда ориентирует на максимизацию выигрыша при наиболее неблагоприятных обстоятельствах. Примером его использования может служить максимальное увеличение минимального дохода, максимизация минимальных объемов наличности и т. п. Такая стратегия оправдывает себя в тех случаях, когда человек, принимающий решения, не столько заинтересован в большой удаче, сколько хочет застраховать себя от внезапных потерь. Другими словами, критерий Вальда сводит риск к минимуму и позволяет принимать наиболее безопасные решения. Подобный подход дает возможность получить гарантированный минимум, хотя фактический итог может оказаться не таким уж и плохим.
Критерий Вальда: пример использования
Предположим, некое предприятие собирается выпускать новые виды товаров. При этом следует сделать выбор между одним из четырех вариантов В1, В2, В3, В4, каждый из которых предполагает определенный тип выпуска либо их сочетание. От принятия решения в конечном счете будет зависеть, какую предприятие получит прибыль. Как конкретно сложится рыночная конъюнктура в будущем, неизвестно, однако аналитики прогнозируют три основных сценария развития событий: С1, С2, С3. Полученные данные позволяют составить таблицу возможных вариантов выигрыша, которые соответствуют каждой паре возможного решения и вероятной обстановки.
|
Виды продукции |
Сценарии рыночной конъюнктуры |
Наихудший результат |
||
|
С1 |
С2 |
С3 |
||
|
В1 |
25 |
37 |
45 |
25 |
|
В2 |
50 |
22 |
35 |
22 |
|
В3 |
41 |
90 |
15 |
15 |
|
В4 |
80 |
32 |
20 |
20 |
Используя критерий Вальда, следует выбрать наилучшую стратегию, такую, которая будет для рассматриваемого предприятия наиболее оптимальной. В нашем случае показатель эффективности
Е = мах {25;22;15;20} = 25.
Его мы получили, выбрав по каждому из вариантов минимальный результат и вычленив среди них тот, который принесет наибольший доход. Это означает, что решение В1 будет для фирмы, согласно данному критерию, самым оптимальным. Даже при самой неблагоприятной обстановке будет получен результат 25 (С1), в то же время не исключено, что он достигнет 45 (С3).
Отметим еще раз, что критерий Вальда ориентирует человека на максимально осторожную линию поведения. При других обстоятельствах вполне возможно руководствоваться иными соображениями. К примеру, вариант В3 мог бы принести выигрыш в 90 при гарантированном результате в 15. Однако этот случай выходит за рамки темы данной статьи, и потому рассматривать его мы пока не будем.
Время на прочтение
18 мин
Количество просмотров 29K
Теория игр — математическая дисциплина, рассматривающая моделирование действий игроков, которые имеют цель, заключающуюся в выбор оптимальных стратегий поведения в условиях конфликта. На Хабре эта тема уже освещалась, но сегодня мы поговорим о некоторых ее аспектах подробнее и рассмотрим примеры на Kotlin.
Так вот, стратегия – это совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации. Оптимальная стратегия игрока – стратегия, обеспечивающая наилучшее положение в данной игре, т.е. максимальный выигрыш. Если игра повторяется неоднократно и содержит, кроме личных, случайные ходы, то оптимальная стратегия обеспечивает максимальный средний выигрыш.
Задача теории игр – выявление оптимальных стратегий игроков. Основное предположение, исходя из которого находятся оптимальные стратегии, заключается в том, что противник (или противники) не менее разумен, чем сам игрок, и делает все для того, чтобы добиться своей цели. Расчет на разумного противника – лишь одна из потенциальных позиций в конфликте, но в теории игр именно она кладется в основу.
Существуют игры с природой в которых есть только один участник, максимизирующий свою прибыль. Игры с природой – математические модели, в которых выбор решения зависит об объективной действительности. Например, покупательский спрос, состояние природы и т.д. «Природа» – это обобщенное понятие не преследующего собственных целей противника. В таком случае для выбора оптимальной стратегии используется несколько критериев.
Различают два вида задач в играх с природой:
- задача о принятии решений в условиях риска, когда известны вероятности, с которыми природа принимает каждое из возможных состояний;
- задачи о принятии решений в условиях неопределенности, когда нет возможности получить информацию о вероятностях появления состояний природы.
Кратко об этих критериях рассказано здесь.
Сейчас мы рассмотрим критерии принятия решений в чистых стратегиях, а в конце статьи решим игру в смешанных стратегиях аналитическим методом.
Оговорочка
Я не являюсь специалистом в теории игр, а в этой работе использовал Kotlin в первый раз. Однако решил поделиться своими результатами. Если вы заметили ошибки в статье или хотите дать совет, прошу в личку.
Постановка задачи
Все критерии принятия решений мы разберем на сквозном примере. Задача такова: фермеру необходимо определить, в каких пропорциях засеять свое поле тремя культурами, если урожайность этих культур, а, значит, и прибыль, зависят от того, каким будет лето: прохладным и дождливым, нормальным, или жарким и сухим. Фермер подсчитал чистую прибыль с 1 гектара от разных культур в зависимости от погоды. Игра определяется следующей матрицей:
Далее эту матрицу будем представлять в виде стратегий:
Искомую оптимальную стратегию обозначим
. Решать игру будем с помощью критериев Вальда, оптимизма, пессимизма, Сэвиджа и Гурвица в условиях неопределенности и критериев Байеса и Лапласа в условиях риска.
Как и говорилось выше примеры будут на Kotlin. Замечу, что вообще-то существуют такие решения как Gambit (написан на С), Axelrod и PyNFG (написанные на Python), но мы будем ехать на своем собственном велосипеде, собранном на коленке, просто ради того, чтобы немного потыкать стильный, модный и молодежный язык программирования.
Чтобы программно реализовать решение игры заведем несколько классов. Сначала нам понадобится класс, позволяющий описать строку или столбец игровой матрицы. Класс крайне простой и содержит список возможных значений (альтернатив или состояний природы) и соответствующего им имени. Поле key будем использовать для идентификации, а также при сравнении, а сравнение понадобится при реализации доминирования.
Строка или столбец игровой матрицы
import java.text.DecimalFormat
import java.text.NumberFormat
open class GameVector(name: String, values: List<Double>, key: Int = -1) : Comparable<GameVector> {
val name: String
val values: List<Double>
val key: Int
private val formatter:NumberFormat = DecimalFormat("#0.00")
init {
this.name = name;
this.values = values;
this.key = key;
}
public fun max(): Double? {
return values.max();
}
public fun min(): Double? {
return values.min();
}
override fun toString(): String{
return name + ": " + values
.map { v -> formatter.format(v) }
.reduce( {f1: String, f2: String -> "$f1 $f2"})
}
override fun compareTo(other: GameVector): Int {
var compare = 0
if (this.key == other.key){
return compare
}
var great = true
for (i in 0..this.values.lastIndex){
great = great && this.values[i] >= other.values[i]
}
if (great){
compare = 1
}else{
var less = true
for (i in 0..this.values.lastIndex){
less = less && this.values[i] <= other.values[i]
}
if (less){
compare = -1
}
}
return compare
}
}
Игровая матрица содержит информацию об альтернативах и состояниях природы. Кроме того в ней реализованы некоторые методы, например нахождение доминирующего множества и чистой цены игры.
Игровая матрица
open class GameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>, natureStateNames: List<String>) {
val matrix: List<List<Double>>
val alternativeNames: List<String>
val natureStateNames: List<String>
val alternatives: List<GameVector>
val natureStates: List<GameVector>
init {
this.matrix = matrix;
this.alternativeNames = alternativeNames
this.natureStateNames = natureStateNames
var alts: MutableList<GameVector> = mutableListOf()
for (i in 0..matrix.lastIndex) {
val currAlternative = alternativeNames[i]
val gameVector = GameVector(currAlternative, matrix[i], i)
alts.add(gameVector)
}
alternatives = alts.toList()
var nss: MutableList<GameVector> = mutableListOf()
val lastIndex = matrix[0].lastIndex // нет провеврки на равенство длин всех строк, считаем что они равны
for (j in 0..lastIndex) {
val currState = natureStateNames[j]
var states: MutableList<Double> = mutableListOf()
for (i in 0..matrix.lastIndex) {
states.add(matrix[i][j])
}
val gameVector = GameVector(currState, states.toList(), j)
nss.add(gameVector)
}
natureStates = nss.toList()
}
open fun change (i : Int, j : Int, value : Double) : GameMatrix{
var mml = this.matrix.toMutableList()
var rowi = mml[i].toMutableList()
rowi.set(j, value)
mml.set(i, rowi)
return GameMatrix(mml.toList(), alternativeNames, natureStateNames)
}
open fun changeAlternativeName (i : Int, value : String) : GameMatrix{
var list = alternativeNames.toMutableList()
list.set(i, value)
return GameMatrix(matrix, list.toList(), natureStateNames)
}
open fun changeNatureStateName (j : Int, value : String) : GameMatrix{
var list = natureStateNames.toMutableList()
list.set(j, value)
return GameMatrix(matrix, alternativeNames, list.toList())
}
fun size() : Pair<Int, Int>{
return Pair(alternatives.size, natureStates.size)
}
override fun toString(): String {
return "Состояния природы:n" +
natureStateNames.reduce { n1: String, n2: String -> "$n1;n$n2" } +
"nМатрица игры:n" +
alternatives
.map { a: GameVector -> a.toString() }
.reduce { a1: String, a2: String -> "$a1;n$a2" }
}
protected fun dominateSet(gvl: List<GameVector>, list: MutableList<String>, dvv: Int) : MutableSet<GameVector>{
var dSet: MutableSet<GameVector> = mutableSetOf()
for (gv in gvl){
for (gvv in gvl){
if (!dSet.contains(gv) && !dSet.contains(gvv)) {
if (gv.compareTo(gvv) == dvv) {
dSet.add(gv)
list.add("[$gvv] доминирует [$gv]")
}
}
}
}
return dSet
}
open fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>)
: GameMatrix{
var result: MutableList<MutableList<Double>> = mutableListOf()
var ralternativeNames: MutableList<String> = mutableListOf()
var rnatureStateNames: MutableList<String> = mutableListOf()
val dIndex = dCol.map { c -> c.key }.toList()
for (i in 0 .. natureStateNames.lastIndex){
if (!dIndex.contains(i)){
rnatureStateNames.add(natureStateNames[i])
}
}
for (gv in this.alternatives){
if (!dRow.contains(gv)){
var nr: MutableList<Double> = mutableListOf()
for (i in 0 .. gv.values.lastIndex){
if (!dIndex.contains(i)){
nr.add(gv.values[i])
}
}
result.add(nr)
ralternativeNames.add(gv.name)
}
}
val rlist = result.map { r -> r.toList() }.toList()
return GameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList())
}
fun dominateMatrix(): Pair<GameMatrix, List<String>>{
var list: MutableList<String> = mutableListOf()
var dCol: MutableSet<GameVector> = dominateSet(this.natureStates, list, 1)
var dRow: MutableSet<GameVector> = dominateSet(this.alternatives, list, -1)
val newMatrix = newMatrix(dCol, dRow)
var ddgm = Pair(newMatrix, list.toList())
val ret = iterate(ddgm, list)
return ret;
}
protected fun iterate(ddgm: Pair<GameMatrix, List<String>>, list: MutableList<String>)
: Pair<GameMatrix, List<String>>{
var dgm = this
var lddgm = ddgm
while (dgm.size() != lddgm.first.size()){
dgm = lddgm.first
list.addAll(lddgm.second)
lddgm = dgm.dominateMatrix()
}
return Pair(dgm,list.toList().distinct())
}
fun minClearPrice(): Double{
val map: List<Double> = this.alternatives.map { a -> a?.min() ?: 0.0 }
return map?.max() ?: 0.0
}
fun maxClearPrice(): Double{
val map: List<Double> = this.natureStates.map { a -> a?.max() ?: 0.0 }
return map?.min() ?: 0.0
}
fun existsClearStrategy() : Boolean{
return minClearPrice() >= maxClearPrice()
}
}Опишем интерфейс, соответствующий критерию
Критерий
interface ICriteria {
fun optimum(): List<GameVector>
}
Принятие решений в условиях неопределенности
Принятие решений в условиях неопределённости предполагает, что игроку не противостоит разумный противник.
Критерий Вальда
В критерии Вальда максимизируется наихудший из возможных результатов:
Использование критерия страхует от наихудшего результата, но цена такой стратегии – потеря возможности получить наилучший из возможных результатов.
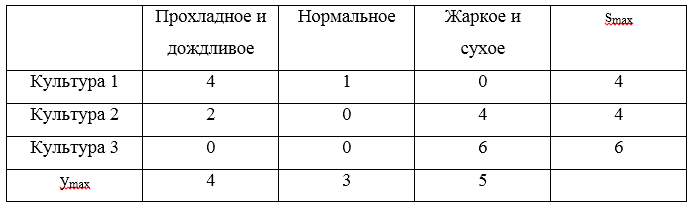
Рассмотрим пример. Для стратегий
найдем минимумы и получим следующую тройку
. Максимумом для указанной тройки будет являться значение 1, следовательно, по критерию Вальда выигрышной стратегией является стратегия
, соответствующая посадке Культуры 2.
Программная реализация критерия Вальда незатейлива:
class WaldCriteria(gameMatrix : GameMatrix) : ICriteria {
val gameMatrix: GameMatrix
init{
this.gameMatrix = gameMatrix
}
override fun optimum(): List<GameVector> {
val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) }
val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)})
return mins
.filter { m -> m.second == max!!.second }
.map { m -> m.first }
}
}
Для большей понятности в первый раз покажу, как решение выглядело бы в виде теста:
Тест
private fun matrix(): GameMatrix {
val alternativeNames: List<String> = listOf("Культура 1", "Культура 2", "Культура 3")
val natureStateNames: List<String> = listOf("Прохладное и дождливое", "Нормальное", "Жаркое и сухое")
val matrix: List<List<Double>> = listOf(
listOf(0.0, 2.0, 5.0),
listOf(2.0, 3.0, 1.0),
listOf(4.0, 3.0, -1.0)
)
val gm = GameMatrix(matrix, alternativeNames, natureStateNames)
return gm;
}
}
private fun testCriteria(gameMatrix: GameMatrix, criteria: ICriteria, name: String){
println(gameMatrix.toString())
val optimum = criteria.optimum()
println("$name. Оптимальная стратегия: ")
optimum.forEach { o -> println(o.toString()) }
}
@Test
fun testWaldCriteria() {
val matrix = matrix();
val criteria = WaldCriteria(matrix)
testCriteria(matrix, criteria, "Критерий Вальда")
}
Нетрудно догадаться, что для других критериев отличие будет только в создании объекта criteria.
Критерий оптимизма
При использовании критерия оптимиста игрок выбирает решение, дающее лучший результат, при этом оптимист предполагает, что условия игры будут для него наиболее благоприятными:
Стратегия оптимиста может привести к отрицательным последствиям, когда максимальное предложение совпадает с минимальным спросом – фирма может получить убытки при списании нереализованной продукции. В тоже время стратегия оптимиста имеет определённый смысл, например, не нужно заботиться о неудовлетворённых покупателях, поскольку любой возможный спрос всегда удовлетворяется, поэтому нет нужды поддерживать расположения покупателей. Если реализуется максимальный спрос, то стратегия оптимиста позволяет получить максимальную полезность в то время, как другие стратегии приведут к недополученной прибыли. Это даёт определённые конкурентные преимущества.
Рассмотрим пример. Для стратегий
найдем найдем максимум и получим следующую тройку
. Максимумом для указанной тройки будет являться значение 5, следовательно, по критерию оптимизма выигрышной стратегией является стратегия
, соответствующая посадке Культуры 1.
Реализация критерия оптимизма почти не отличается от критерия Вальда:
class WaldCriteria(gameMatrix : GameMatrix) : ICriteria {
val gameMatrix: GameMatrix
init{
this.gameMatrix = gameMatrix
}
override fun optimum(): List<GameVector> {
val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) }
val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)})
return mins
.filter { m -> m.second == max!!.second }
.map { m -> m.first }
}
}
Критерий пессимизма
Данный критерий предназначен для выбора наименьшего элемента игровой матрицы из ее минимально возможных элементов:
Критерий пессимизма предполагает, что развитие событий будет неблагоприятным для лица, принимающего решение. При использовании этого критерия лицо принимающее решение ориентируется на возможную потерю контроля над ситуацией, поэтому, старается исключить потенциальные риски выбирая вариант с минимальной доходностью.
Рассмотрим пример. Для стратегий
найдем найдем минимум и получим следующую тройку
. Минимумом для указанной тройки будет являться значение -1, следовательно, по критерию пессимизма выигрышной стратегией является стратегия
, соответствующая посадке Культуры 3.
После знакомства с критериями Вальда и оптимизма то, как будет выглядеть класс критерия пессимизма, думаю, легко догадаться:
class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria {
val gameMatrix: GameMatrix
init{
this.gameMatrix = gameMatrix
}
override fun optimum(): List<GameVector> {
val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) }
val min = mins.minWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)})
return mins
.filter { m -> m.second == min!!.second }
.map { m -> m.first }
}
}
Критерий Сэвиджа
Критерий Сэвиджа (критерий сожалеющего пессимиста) предполагает минимизацию наибольшей потерянной прибыли, иными словами минимизируется наибольшее сожаление по потерянной прибыли:
В данном случае S — это матрица сожалений.
Оптимальное решение по критерию Сэвиджа должно давать наименьшее сожаление из найденных на предыдущем шаге решения сожалений. Решение, соответствующее найденной полезности, будет оптимальным.
К особенностям полученного решения относятся гарантированное отсутствие самых больших разочарований и гарантированное снижение максимальных возможных выигрышей других игроков.
Рассмотрим пример. Для стратегий
составим матрицу сожалений:
Тройка максимальных сожалений
. Минимальным значением из указанных рисков будет являться значение 4, которое соответствует стратегиям
и
.
Запрограммировать критерий Сэвиджа немного сложнее:
class SavageCriteria(gameMatrix: GameMatrix) : ICriteria {
val gameMatrix: GameMatrix
init {
this.gameMatrix = gameMatrix
}
fun GameMatrix.risk(): List<Pair<GameVector, Double?>> {
val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) }
.map { n -> n.first.key to n.second }.toMap()
var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf()
for (a in this.alternatives) {
var v: MutableList<Double> = mutableListOf()
for (i in 0..a.values.lastIndex) {
val mn = maxStates.get(i)
v.add(mn!! - a.values[i])
}
am.add(Pair(a, v.toList()))
}
return am.map { m -> Pair(m.first, m.second.max()) }
}
override fun optimum(): List<GameVector> {
val risk = gameMatrix.risk()
val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) })
return risk
.filter { r -> r.second == minRisk!!.second }
.map { m -> m.first }
}
}
Критерий Гурвица
Критерий Гурвица является регулируемым компромиссом между крайним пессимизмом и полным оптимизмом:
A(0) — стратегия крайнего пессимиста, A(k) — стратегия полного оптимиста,
— задаваемое значение весового коэффициента:
;
— крайний пессимизм,
— полный оптимизм.
При небольшом числе дискретных стратегий, задавая желаемое значение весового коэффициента
, а затем округлять получаемый результат до ближайшего возможного значения с учётом выполненной дискретизации.
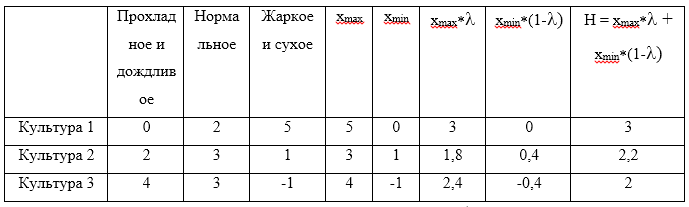
Рассмотрим пример. Для стратегий
. Примем, что коэффициент оптимизма
. Теперь составим таблицу:
Максимальным значением из рассчитанных H будет являться значение 3, которое соответствует стратегии
.
Реализация критерия Гурвица уже более объемная:
class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria {
val gameMatrix: GameMatrix
val optimisticKoef: Double
init {
this.gameMatrix = gameMatrix
this.optimisticKoef = optimisticKoef
}
inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){
val xmax: Double
val xmin: Double
val optXmax: Double
val value: Double
init{
this.xmax = xmax
this.xmin = xmin
this.optXmax = optXmax
value = xmax * optXmax + xmin * (1 - optXmax)
}
}
fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> {
return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) }
}
override fun optimum(): List<GameVector> {
val hpar = gameMatrix.getHurwitzParams()
val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) })
return hpar
.filter { r -> r.second == maxHurw!!.second }
.map { m -> m.first }
}
}
Принятие решений в условиях риска
Методы принятия решений могут полагаться на критерии принятия решений в условиях риска при соблюдении следующих условий:
- отсутствия достоверной информации о возможных последствиях;
- наличия вероятностных распределений;
- знания вероятности наступления исходов или последствий для каждого решения.
Если решение принимается в условиях риска, то стоимости альтернативных решений описываются вероятностными распределениями. В связи с этим принимаемое решение основывается на использовании критерия ожидаемого значения, в соответствии с которым альтернативные решения сравниваются с точки зрения максимизации ожидаемой прибыли или минимизации ожидаемых затрат.
Критерий ожидаемого значения может быть сведен либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат. В данном случае предполагается, что связанная с каждым альтернативным решением прибыль (затраты) является случайной величиной.
Постановка таких задач как правило такова: человек выбирает какие-либо действия в ситуации, где на результат действия влияют случайные события. Но игрок имеет некоторые знания о вероятностях этих событий и может рассчитать наиболее выгодную совокупность и очередность своих действий.
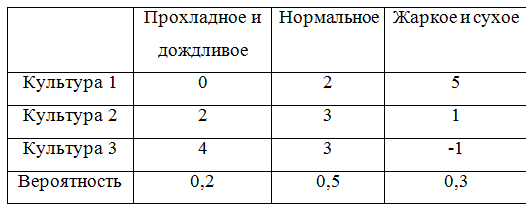
Чтобы можно было и дальше приводить примеры, дополним игровую матрицу вероятностями:
Для того, чтобы учесть вероятности придется немного переделать класс, описывающий игровую матрицу. Получилось, по правде говоря, не очень-то изящно, ну да ладно.
Игровая матрица с вероятностями
open class ProbabilityGameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>,
natureStateNames: List<String>, probabilities: List<Double>) :
GameMatrix(matrix, alternativeNames, natureStateNames) {
val probabilities: List<Double>
init {
this.probabilities = probabilities;
}
override fun change (i : Int, j : Int, value : Double) : GameMatrix{
val cm = super.change(i, j, value)
return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities)
}
override fun changeAlternativeName (i : Int, value : String) : GameMatrix{
val cm = super.changeAlternativeName(i, value)
return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities)
}
override fun changeNatureStateName (j : Int, value : String) : GameMatrix{
val cm = super.changeNatureStateName(j, value)
return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities)
}
fun changeProbability (j : Int, value : Double) : GameMatrix{
var list = probabilities.toMutableList()
list.set(j, value)
return ProbabilityGameMatrix(matrix, alternativeNames, natureStateNames, list.toList())
}
override fun toString(): String {
var s = ""
val formatter: NumberFormat = DecimalFormat("#0.00")
for (i in 0 .. natureStateNames.lastIndex){
s += natureStateNames[i] + " = " + formatter.format(probabilities[i]) + "n"
}
return "Состояния природы:n" +
s +
"Матрица игры:n" +
alternatives
.map { a: GameVector -> a.toString() }
.reduce { a1: String, a2: String -> "$a1;n$a2" }
}
override fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>)
: GameMatrix{
var result: MutableList<MutableList<Double>> = mutableListOf()
var ralternativeNames: MutableList<String> = mutableListOf()
var rnatureStateNames: MutableList<String> = mutableListOf()
var rprobailities: MutableList<Double> = mutableListOf()
val dIndex = dCol.map { c -> c.key }.toList()
for (i in 0 .. natureStateNames.lastIndex){
if (!dIndex.contains(i)){
rnatureStateNames.add(natureStateNames[i])
}
}
for (i in 0 .. probabilities.lastIndex){
if (!dIndex.contains(i)){
rprobailities.add(probabilities[i])
}
}
for (gv in this.alternatives){
if (!dRow.contains(gv)){
var nr: MutableList<Double> = mutableListOf()
for (i in 0 .. gv.values.lastIndex){
if (!dIndex.contains(i)){
nr.add(gv.values[i])
}
}
result.add(nr)
ralternativeNames.add(gv.name)
}
}
val rlist = result.map { r -> r.toList() }.toList()
return ProbabilityGameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList(),
rprobailities.toList())
}
}
}
Критерий Байеса
Критерий Байеса (критерий математического ожидания) используется в задачах принятия решения в условиях риска в качестве оценки стратегии
выступает математическое ожидание соответствующей ей случайной величины. В соответствии с этим правилом оптимальная стратегия игрока
находится из условия:
Иными словами, показателем неэффективности стратегии
по критерию Байеса относительно рисков является среднее значение (математическое ожидание ожидание) рисков i-й строки матрицы
, вероятности которых, совпадают с вероятностями природы. Тогда оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия
, обладающая минимальной неэффективностью то есть минимальным средним риском. Критерий Байеса эквивалентен относительно выигрышей и относительно рисков, т.е. если стратегия
является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот.
Перейдем к примеру и рассчитаем математические ожидания:
Максимальным математическим ожиданием является
, следовательно, выигрышной стратегией является стратегия
.
Программная реализация критерия Байеса:
class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria {
val gameMatrix: ProbabilityGameMatrix
init {
this.gameMatrix = gameMatrix
}
fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> {
var am: MutableList<Pair<GameVector, Double>> = mutableListOf()
for (a in this.alternatives) {
var alprob: Double = 0.0
for (i in 0..a.values.lastIndex) {
alprob += a.values[i] * this.probabilities[i]
}
am.add(Pair(a, alprob))
}
return am.toList();
}
override fun optimum(): List<GameVector> {
val risk = gameMatrix.bayesProbability()
val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) })
return risk
.filter { r -> r.second == maxBayes!!.second }
.map { m -> m.first }
}
}Критерий Лапласа
Критерий Лапласа представляет упрощенную максимизацию математического ожидания полезности, когда справедливо предположение о равной вероятности уровней спроса, что избавляет от необходимости сбора реальной статистики.
В общем случае при использовании критерия Лапласа матрица ожидаемых полезностей и оптимальный критерий определяются следующим образом:
Рассмотрим пример принятия решений по критерию Лапласа. Рассчитаем среднеарифметическое для каждой стратегии:
Таким образом, выигрышной стратегией является стратегия
.
Программная реализация критерия Лапласа:
class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria {
val gameMatrix: GameMatrix
init {
this.gameMatrix = gameMatrix
}
fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> {
return this.alternatives.map { m -> Pair(m, m.values.average()) }
}
override fun optimum(): List<GameVector> {
val risk = gameMatrix.arithemicMean()
val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) })
return risk
.filter { r -> r.second == maxBayes!!.second }
.map { m -> m.first }
}
}Смешанные стратегии. Аналитический метод
Аналитический метод позволяет решить игру в смешанных стратегиях. Для того, чтобы сформулировать алгоритм нахождения решения игры аналитическим методом, рассмотрим некоторые дополнительные понятия.
Стратегия
доминирует стратегию
, если все
. Иными словами, если в некоторой строке платёжной матрицы все элементы больше или равны соответствующим элементам другой строки, то первая строка доминирует вторую и называется доминант-строкой. А также если в некотором столбце платёжной матрицы все элементы меньше или равны соответствующим элементам другого столбца, то первый столбец доминирует второй и называется доминант-столбцом.
Нижней ценой игры называется
.
Верхней ценой игры называется
.
Теперь можно сформулировать алгоритм решения игры аналитическим методом:
- Вычислить нижнюю
и верхнюю
цены игры. Если
, то записать ответ в чистых стратегиях, если нет — продолжаем решение дальше
- Удалить доминирующие строки доминирующие столбцы. Их может быть несколько. На их место в оптимальной стратегии соответствующие компоненты будут равны 0
- Решить матричную игру методом линейного программирования.
Для того, чтобы привести пример необходимо привести класс, описывающий решение
Solve
class Solve(gamePriceObr: Double, solutions: List<Double>, names: List<String>) {
val gamePrice: Double
val gamePriceObr: Double
val solutions: List<Double>
val names: List<String>
private val formatter: NumberFormat = DecimalFormat("#0.00")
init{
this.gamePrice = 1 / gamePriceObr
this.gamePriceObr = gamePriceObr;
this.solutions = solutions
this.names = names
}
override fun toString(): String{
var s = "Цена игры: " + formatter.format(gamePrice) + "n"
for (i in 0..solutions.lastIndex){
s += "$i) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "n"
}
return s
}
fun itersect(matrix: GameMatrix): String{
var s = "Цена игры: " + formatter.format(gamePrice) + "n"
for (j in 0..matrix.alternativeNames.lastIndex) {
var f = false
val a = matrix.alternativeNames[j]
for (i in 0..solutions.lastIndex) {
if (a.equals(names[i])) {
s += "$j) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "n"
f = true
break
}
}
if (!f){
s += "$j) " + a + " = 0n"
}
}
return s
}
}И класс, выполняющий решение симплекс-методом. Поскольку в математике я не разбираюсь, то воспользовался готовой реализацией из Apache Commons Math
Solver
open class Solver (gameMatrix: GameMatrix) {
val gameMatrix: GameMatrix
init{
this.gameMatrix = gameMatrix
}
fun solve(): Solve{
val goalf: List<Double> = gameMatrix.alternatives.map { a -> 1.0 }
val f = LinearObjectiveFunction(goalf.toDoubleArray(), 0.0)
val constraints = ArrayList<LinearConstraint>()
for (alt in gameMatrix.alternatives){
constraints.add(LinearConstraint(alt.values.toDoubleArray(), Relationship.LEQ, 1.0))
}
val solution = SimplexSolver().optimize(f, LinearConstraintSet(constraints), GoalType.MAXIMIZE,
NonNegativeConstraint(true))
val sl: List<Double> = solution.getPoint().toList()
val solve = Solve(solution.getValue(), sl, gameMatrix.alternativeNames)
return solve
}
}
Теперь выполним решение аналитическим методом. Для наглядности возьмем другую игровую матрицу:
В этой матрице есть доминирующее множество:
begin{pmatrix} 2& 4\ 6& 2end{pmatrix}
Решение
val alternativeNames: List<String> = listOf("Культура 1", "Культура 2", "Культура 3")
val natureStateNames: List<String> =
listOf("Прохладное и дождливое", "Нормальное", "Жаркое и сухое", "Ветреное")
val matrix: List<List<Double>> = listOf(
listOf(2.0, 4.0, 8.0, 5.0),
listOf(6.0, 2.0, 4.0, 6.0),
listOf(3.0, 2.0, 5.0, 4.0)
)
val gm = GameMatrix(matrix, alternativeNames, natureStateNames)
val (dgm, list) = gm.dominateMatrix()
println(dgm.toString())
println(list.reduce({s1, s2 -> s1 + "n" + s2}))
println()
val s: Solver = Solver(dgm)
val solve = s.solve()
println(solve)
Решение игры
при цене игры равной 3,33
Вместо заключения
Надеюсь, эта статья будет полезна тем, кому необходимо в первом приближении с решением игр с природой. Вместо выводов ссылка на GitHub.
Буду благодарен за конструктивную обратную связь!