Как найти кпд станции

ГЛАВА 7

ТЕПЛОВЫЕ
ЭЛЕКТРИЧЕСКИЕ СТАНЦИИ

§ 7.1. ПОКАЗАТЕЛИ
РЕЖИМА РАБОТЫ ЭЛЕКТРИЧЕСКИХ СТАНЦИЙ

Характерной
особенностью режима эксплуатации
электричес­ких станций является
строгое соответствие производства
элект­рической и тепловой энергии ее
потреблению. Поэтому для обес­печения
надежной работы электростанции необходимо
знать из­менение потребления энергии
по времени. Изменение потребле­ния
энергии по времени изображается
диаграммой, которая на­зывается
графиком
нагрузки. Графики
нагрузки могут быть су­точными,
месячными и годовыми. На рис. 7.1 изображен
годовой график электрической нагрузки.
На графике по оси абсцисс от­кладывается
продолжительность нагрузки в часах за
год (1 год — 365·24 = 8760 ч), а по оси ординат
— нагрузка в кВт.

Площадь, ограниченная
кривой годового графика (рис. 7.1),
представляет собой в масштабе количество
выработанной стан­цией за год энергии
в киловатт-часах. Определив площадь F
(м²)
под кривой годового графика, находят
количество выработанной энергии (кВт·ч)
станцией за год:

Э=Fm, (7.1)

где m
— масштаб
графика, кВт·ч/м².

Режим
работы электрических станций оценивается
коэффици­ентом использования
установленной мощности, коэффициентом

нагрузки,
коэффициентом резер­ва, числом часов
использования установленной мощности
и чис­лом часов использования макси­мума
нагрузки.

Коэффициент
использова­ния установленной мощности
k_и
представляет
собой отноше­ние количества выработанной
энергии за год Э
к установ­ленной мощности электростан­ции
N

k_и=Э/(8760N)=N/N,
(7.2)

где N
— средняя
нагрузка электростанции, кВт.

Средняя нагрузка
электростанции (кВт)

N=Э/8760. (7.3)

Коэффициент
нагрузки k_н
представляет
собой отношение сре­дней нагрузки
электростанции N
к максимальной
N,
т. е.

k_н=N/N, (7.4)

Коэффициент резерва
k_p
представляет
собой отношение уста­новленной
мощности электростанции N
к максимальной
на­грузке
N:

k_p=N/N, (7.5)

или

k_p=k_н/k_и (7.6)

Число часов
использования установленной мощности
Т_у
пред­ставляет
собой отношение количества выработанной
энергии за год Э
к установленной
мощности станции N:

T_y=Э/N. (7.7)

Число часов
использования максимума нагрузки Т_м
представ­ляет
собой отношение количества выработанной
энергии за год Э
к максимальной нагрузке электростанции
N,
т. е.

T_м=
Э/N. (7.8)

Задача 7.1.
На электростанции установлены три
турбогенера­тора мощностью N=50·10³
кВт каждый. Определить количест­во
выработанной энергии за год и коэффициент
использования установленной мощности,
если площадь под кривой годового графика
нагрузки станции F=9,2·10^-4
м²
и масштаб графика т=9·10¹¹
кВт·ч/м².

Ответ: Э=8,28·10⁸
кВт·ч; k_и=0,63.

Задача 7.2.
На электростанции установлены два
турбогенера­тора мощностью N=25·10³
кВт каждый. Определить среднюю нагрузку
станции и коэффициент использования
установленной мощности, если количество
выработанной энергии за год Э=30·10⁷
кВт·ч.

Ответ: N=34245
кВт; k_и=0,685.

Задача 7.3.
Определить
число часов использования установ­ленной
мощности и коэффициент нагрузки
электростанции, если установленная
мощность электростанции N=16·10⁴
кВт, мак­симальная нагрузка станции
N=13,6·10⁴
кВт, площадь под кривой годового графика
нагрузки станции F=
8·10^-4
м²
и мас­штаб графика m=1·10¹²
кВт·ч/м².

Ответ: T_у=5000
ч; k_н=0,67.

Задача 7.4.
Определить
число часов использования максиму­ма
нагрузки и коэффициент резерва
электростанции, если пло­щадь под
кривой годового графика нагрузки станции
F=8,5·10^-4
м²,
масштаб графика т=8,8·10¹¹
кВт·ч/м²,
число часов использования установленной
мощности Т_у=5500
ч и мак­симальная нагрузка станции
N=12,5·10⁴
кВт.

Ответ: T_м=5984
ч; k_р=1,09.

Задача 7.5.
На электростанции установлены два
турбогене­ратора мощностью N=75·10³
кВт каждый. Определить пока­затели
режима работы станции, если максимальная
нагруз­ка станции N=135·10³
кВт, площадь под кривой годового графика
нагрузки F=9,06·10^-4
м²
и масштаб графика т=8,7·10¹¹
кВт·ч/м².

Решение:
Количество выработанной электрической
энергии за год станцией определяем по
формуле (7.1):

Э=Fm=9,06·10^-4·8,7·10¹¹=788,2·10⁶
кВт·ч.

Средняя нагрузка
электростанции, по формуле (7.3),

N=Э/8760=788,2·10⁶/8760=9·10⁴
кВт.

Установленная
мощность электростанции

N=2N=2·75·10³=150·10³
кВт.

Коэффициент
использования установленной мощности
опре­деляем по формуле (7.2):

k_и=N/N=9·10⁴/(150·10³)=0,6.

Коэффициент
нагрузки, по формуле (7.4),

k_н=N/N=9·10⁴/(135·10³)=0,666.

Коэффициент
резерва, по формуле (7.6),

k_p=k_н/k_и=0,666/0,6=1,11.

Число часов
использования установленной мощности,
по формуле (7.7),

T_y=Э/N=788,2·10⁶/150·10³=5255
ч.

Число часов
использования максимума нагрузки, по
формуле (7.8),

T_м=
Э/N=788,2·10⁶/135·10³=5840
ч.

Задача 7.6.
На электростанции установлены три
турбогенера­тора мощностью N=50·10³
кВт каждый. Определить число ча­сов
использования установленной мощности
и коэффициент резе­рва станции, если
количество выработанной энергии за год
Э=788,4·10⁶
кВт·ч и коэффициент нагрузки k_н=0,69.

Ответ: T_у=5256
ч; k_p=1,15.

Задача 7.7.
На электростанции установлены три
турбогенера­тора мощностью N=25·10³
кВт каждый. Определить коэффици­енты
использования установленной мощности,
нагрузки и резер­ва, если количество
выработанной энергии за год Э=394,2·10⁶
кВт·ч и максимальная нагрузка станции
N=65,2·10³
кВт.

Ответ: k_и=0,6;
k_н=0,69;
k_p=1,15.

Задача 7.8.
На электростанции установлены три
турбогенера­тора мощностью N=1·10⁴
кВт каждый. Определить показатели режима
работы станции, если количество
выработанной энергии за год Э=178,7·10⁶
кВт·ч и максимальная нагрузка станции
N=28,3·10³
кВт.

Ответ: k_и=0,68;
k_н=0,72;
k_p=1,06;
T_у=5957
ч; T_м=6315
ч.

§ 7.2. ПОКАЗАТЕЛИ,
ХАРАКТЕРГОУЮЩИЕ ЭКОНОМИЧНОСТЬ ТЕПЛОВЫХ
ЭЛЕКТРИЧЕСКИХ СТАНЦИЙ

Экономичность
работы электрической станции оценивается
коэффициентами полезного действия,
удельным расходом усло­вного топлива,
удельным расходом теплоты на выработку
элект­роэнергии и себестоимостью
энергии.

Кпд электростанции
подразделяются на кпд брутто, опреде­ляемый
без учета расхода энергии на собственные
нужды, и кпд нетто — с учетом расхода
электрической энергии и теплоты на
собственные нужды.

Кпд конденсационной
электростанции (КЭС) брутто η
представляет собой отношение количества
выработанной электроэнергии к энергии,
подведенной с топливом:

η=Э^выр/(BQ), (
7.9)

где Э^выр
— количество выработанной электроэнергии,
кДж; В —
расход топлива, кг; Q
— низшая
теплота сгорания рабочей массы топлива,
кДж/кг.

Если известны кпд
отдельных узлов и установок электростан­ции,
то без учета работы питательных насосов
кпд КЭС брутто может быть определен по
формуле

η=η_куη_трη_tη_oiη_мη_г, (7.10)

где η_ку
— кпд
котельной установки; η_тр
— кпд трубопроводов; η_oi
— термический
кпд цикла Ренкина при заданных параметрах
пара на электростанции; η_t
— относительный
внутренний кпд турбины; η_м
— механический
кпд турбины; η_г
— электрический
кпд генератора.

Кпд конденсационной
электростанции нетто η
представля­ет
собой отношение отпущенной электроэнергии
к энергии, под­веденной с топливом:

η=Э^отп/(BQ), (7.11)

где Э^отп=Э^выр—Э^сн
— количество отпущенной электроэнергии,
равное разности выработанной и
израсходованной на собствен­ные
нужды, кДж.

Для теплоэлектроцентралей
(ТЭЦ) применяются частные кпд по выработке
электроэнергии η
и теплоты
η.

Кпд ТЭЦ брутто по
выработке электроэнергии определяется
по формуле

η=Э^выр/(B_эQ), (7.12)

где В_э
— расход
топлива на выработку электроэнергии,
кг.

Кпд ТЭЦ брутто по
выработке теплоты находится по фор­муле

η=Q^отп/(B_QQ), (7.13)

где Q^отп
— количество теплоты, отпускаемое
потребителям, кДж; В_Q
— расход
топлива на выработку отпущенной теплоты,
кг.

Кпд ТЭЦ нетто по
отпуску электроэнергии определяется
по формуле

η=Э^отп/[(B_э—B_сн)Q], (7.14)

где В_сн
— расход
топлива на выработку электроэнергии
для со­бственных нужд, потребляемой
в связи с отпуском теплоты, кг. Кпд ТЭЦ
нетто по отпуску теплоты находится по
формуле

η=Q^отп/[(B_Q+B_сн)Q]. (7.15)

Удельный расход
условного топлива (кг/МДж) на КЭС на
выработку 1 МДж (10³кДж)
электроэнергии определяется по формуле

b=BQ/(29,33Э^выр)=0,0342/η. (7.16)

Удельный расход
условного топлива [кг/(кВт·ч)] на КЭС на
выработку 1 кВт·ч электроэнергии
находится по формуле

b=3600BQ/(29300Э^выр)=0,123/η. (7.17)

Удельный расход
условного топлива (кг/МДж) на ТЭЦ на
выработку 1 МДж электроэнергии определяется
по формуле

b=B_эQ/(29,33Э^выр)=0,0342/η.
(7.18)

Удельный расход
условного топлива [кг/(кВт·ч)] на ТЭЦ на
выработку 1 кВт·ч электроэнергии
находится по формуле

b=3600B_эQ/(29300Э^выр)=0,123/η.
(7.19)

Удельный расход
условного топлива (кг/МДж) на ТЭЦ на
выработку 1 МДж теплоты определяется
по формуле

b=B_QQ/(29,33Q^отп)=0,0342/η. (7.20)

Удельный расход
теплоты [МДж/(кВт·ч)] на выработку
элект­роэнергии на КЭС находится по
формуле

d
=Qb, (7.21)

или

d=1/η. (7.22)

Удельный расход
теплоты [МДж/(кВт·ч)] на выработку
элект­роэнергии на ТЭЦ определяется
по формуле

d
=Qb,
(7.23)

или

d=1/η.
(7.24)

Расход топлива на
ТЭЦ (кг)

В_ТЭЦ=В_э+В_Q. (7.25)

Расход топлива
(кг) на выработку отпущенной теплоты
нахо­дится по формуле

В_Q=Q^отп/(Qη_ку). (7.26)

Расход топлива
(кг) на ТЭЦ может быть определен по
формуле

В_ТЭЦ=D/И, (7.27)

где И
— испарительность
топлива, кг/кг; D
— расход
пара на ТЭЦ, кг.

Коэффициент
использования теплоты топлива на ТЭЦ
оцени­вает эффективность использования
топлива

η_ТЭЦ=(Q^отп+Э^выр)/(В_ТЭЦQ). (7.28)

Кпд атомной
электростанции определяется по формуле

η_АЭС=η_рη_трη_tη_oiη_мη_г, (7.29)

где η_р
— кпд
реактора; η_тр
— кпд теплового потока; η_t
— тер­мический кпд; η_oi
—
относительный внутренний кпд турбины;
η_м
— механический кпд; η_г
— кпд
электрогенератора.

Удельный расход
ядерного топлива [кг/(кВт·ч)] на атомной
электростанции (АЭС) находится по формуле

b_АЭС=1/(24·10³kη_АЭС), (7.30)

где k
— средняя
глубина горючего, МВт·сут/кг урана.

Себестоимость 1
кВт·ч электроэнергии [коп/(кВт·ч)]
отпуска­емой КЭС, определяется по
формуле

S=ΣИ/Э^отп=[(И_топ+И_ам+И_зп+ΣИ_пр)/Э^отп]100, (7.31)

где ΣИ
— сумма затрат, руб/год; И_топ
— затраты на топливо, руб/год; И_ам
— затраты
на амортизацию, руб/год; И_зп
— затра­ты на заработную плату,
руб/год; И_пр
— все остальные статьи затрат, руб/год.

Себестоимость 1
кВт·ч электроэнергии [коп/(кВт·ч)]
отпуска­емой ТЭЦ, находится по формуле

S=В_эΣИ/(В_ТЭЦЭ^отп)=[В_э(И_топ+И_ам+И_зп+ΣИ_пр)/В_ТЭЦЭ^отп]100. (7.32)

Задача 7.9.
Конденсационная станция израсходовала
В=720·10⁶
кг/год каменного угля с низшей теплотой
сгорания Q=20500
кДж/кг и выработала электроэнергии
Э^выр=590·10¹⁰
кДж/год, израсходовав при этом на
собственные нужды 5% от выработанной
электроэнергии. Определить кпд брутто
и кпд нетто станции.

Ответ: η=0,4;
η=0,38.

Задача 7.10.
Определить кпд конденсационной
электростан­ции брутто без учета
работы питательных насосов, если кпд
котельной установки η_ку=0,89,
кпд трубопроводов η_тр=0,97,
от­носительный внутренний кпд турбины
η_oi=0,84,
механический кпд турбины η_м=0,98,
электрический кпд генератора η_г=0,98,
начальные параметры пара перед турбинами
р₁=9
МПа, t₁=550°С
и давление пара в конденсаторе р_к=4·10³
Па.

Ответ:
η=0,3.

Задача 7.11.
Конденсационная электростанция работает
при начальных параметрах пара перед
турбинами р₁=8,8
МПа, t₁=535°С
и давлении пара в конденсаторе р_к=4·10³
Па. Опреде­лить, на сколько повысится
кпд станции брутто без учета работы
питательных насосов с увеличением
начальных параметров пара до р=10
МПа и t=560°C,
если изве­стны кпд котельной установки
η_ку=0,9,
кпд трубопроводов η_тр=0,97,
относительный внутрен­ний кпд турбины
η_oi=0,84,
механи­ческий кпд турбины η_м=0,98
и электрический кпд генерато­ра
η_г=0,98.

Решение:
Энтальпию пара i₁
при заданных начальных парамет­рах
пара p₁
и t₁
и энтальпию пара i₂
в конце
адиабатного расширения находим по
is-диаграмме
(рис. 7.2): i₁=3480
кДж/кг; i₂=2030
кДж/кг. Энтальпию конденсата при давле­нии
р_к=4·10³
Па определяем
по табл. 2 (см. Приложение): i=121,33
кДж/кг.

Термический кпд
установки при начальных параметрах
пара p₁
и t₁
находим по
формуле

η_t=(i₁—i₂)/(i₁—i)=(3480-2030)/(3480-121,33)=0,432.

Кпд КЭС брутто при
начальных параметрах пара р₁
и t₁
опре­деляем
по формуле (7.10):

η=η_куη_трη_tη_oiη_мη_г=0,9·0,97·0,432·0,84·0,98·0,98=0,304.

Энтальпию пара i
при начальных
параметрах пара р
и t,
энтальпию
пара i
в конце адиабатного расширения находим
по is-диаграмме
(рис. 7.2): i=3540
кДж/кг; i=2050
кДж/кг.

Термический кпд
установки при начальных параметрах
пара р
и t
находим по формуле

η=(i—i)/(i—i)=(3540-2050)/(3540-121,33)=0,436.

Кпд КЭС брутто при
начальных параметрах пара р
и t,
по формуле
(7.10),

η=η_куη_трηη_oiη_мη_г=0,9·0,97·0,436·0,84·0,98·0,98=0,307.

Следовательно,
кпд КЭС брутто повысится на

Δη=η—η=0,307-0,304=0,003,
или на 1%.

Задача 7.12.
Теплоэлектроцентраль израсходовала
B_ТЭЦ=94·10⁶
кг/год каменного угля с низшей теплотой
сгорания Q=24700
кДж/кг, выработав при этом электроэнергии
Э^выр=61·10¹⁰
кДж/год и отпустив теплоту внешним
потребите­лям Q^отп=4,4·10¹¹
кДж/год. Определить кпд ТЭЦ брутто по
выработке электроэнергии и теплоты,
если расход топли­ва на выработку
отпущенной теплоты составляет B_Q=23·10⁶
кг/год.

Ответ: η=0,348;
η=0,775.

Задача 7.13.
Теплоэлектроцентраль израсходовала
B_ТЭЦ=72·10⁶
кг/год каменного угля с низшей теплотой
сгорания Q=25500
кДж/кг, выработав при этом электроэнергии
Э^выр=48·10¹⁰
кДж/год и отпустив теплоту внешним
потребителям Q^отп=3,1·10¹¹
кДж/год. Определить кпд ТЭЦ брутто по
выра­ботке электроэнергии и теплоты,
если кпд котельной установки η_ку=0,88.

Ответ: η=0,33;
η=0,88.

Задача 7.14.
Теплоэлектроцентраль израсходовала
B_ТЭЦ=82·10⁶
кг/год бурого угля с низшей теплотой
сгорания Q=15800
кДж/кг, выработав при этом электроэнергии
Э^выр=38·10¹⁰
кДж/год и отпустив теплоты внешним
потреби­телям Q^отп=3,2·10¹¹
кДж/год.
Определить кпд ТЭЦ нетто по отпуску
электроэнергии и теплоты, если расход
электроэнергии на собственные нужды
8% от выработанной энергии, расход топлива
на выработку отпущенной теплоты B_Q=20·10⁶
кг/год и расход топлива на выработку
электроэнергии для собственных нужд
В_сн=4,6·10⁶
кг/год.

Соседние файлы в папке задачи по турбинам

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ЭЛЕКТРОСТАНЦИЙ

2.1.
КПД конденсационных электростанций

Основным
показателем энергетической эффективности станции является КПД по отпуску
электрической энергии – абсолютный электрический КПД . Он равен отношению отпущенной (производственной)
электроэнергии к затраченной энергии (теплоте сожженного топлива) Q_с,
называется КПД нетто станции .

;                                         (2.1)

                                        , 

где Э – выработка электроэнергии;  – расход
электроэнергии на собственные нужды;  – доля расхода
электроэнергии на собственные нужды. η_пк;  Q_пк – КПД и
тепловая нагрузка парового котла; В –
расход топлива на электростанции; Э, Э_сн, Q_с – относятся к любому промежутку времени и выражены в
одинаковых электрических или тепловых единицах.

Для
часового промежутка времени  равен

 ,                                              
(2.2)

где N_э –
электрическая мощность турбины, кВт.

При
планировании и отчетности используют , при анализе энергетической эффективности станции – КПД
брутто

;                                                 
(2.3)

.                                                    
(2.4)

Для
КЭС: , , .

2.2. Цикл Ренкина в T, S и i, S диаграммах

Основой
технологического процесса выработки энергии паровой турбиной является цикл
Ренкина (рис. 2.1, 2.2), состоящий из изобар подвода и отвода тепла и адиабат
(изоэнтроп) работы пара в турбине и работы питательного насоса:

1–2 – адиабатное расширение пара в турбоустановке; 2–3 –
конденсация пара в конденсаторе; 3–4 – сжатие воды в конденсатном и питательном
насосах; 4–5 – подогрев воды до температуры насыщения t_s в регенеративном подогревателе и
водяном экономайзере; 5–6 – превращение воды в пар; 6–1 – перегрев пара в пароперегревателе
(ПП).

Термический
КПД цикла Ренкина:

 ,                                  (2.5)                             

где Q₀=i₀ – i_пв – расход
тепла из горячего источника; Q_ка – потеря
тепла в холодном источнике (при адиабатном расширении); i₀, i_пв, i_ка, i¢_к –
соответственно энтальпия свежего пара, основного конденсата после сжатия в питательном
насосе, отработавшего пара при изоэнтропийном (адиабатном) расширении и конденсата
отработавшего пара при насыщении, кДж/кг.

Формулу
(2.5) запишем в виде

,             
(2.6)              

где Н_а – адиабатное (располагаемое)
теплопадение пара; h_на=i_пв – i¢_к– изоэнтропийная
работа насоса, эквивалентная подогреву воды в нем; Q¢₀ – расход
тепла на турбину без учета работы питательного насоса.

Если не
учитывать работу питательного насоса, то

  .            (2.7)                               

Расход
энергии на повышение давления воды в насосе составляет 3¸4 % работы
пара в турбине (25¸35 кДж/кг).
Таким образом, работа питательного насоса – основная составляющая расхода
энергии на собственные нужды электростанции.

2.3. Основные составляющие абсолютного КПД КЭС

КПД
КЭС (рис. 2.3) зависит от КПД турбоустановки , парового котла  и соединяющих их
трубопроводов пара и воды .

Абсолютный
электрический КПД турбоустановки

,                      
(2.8)                                                 

где Q_ту – расход
теплоты пара на турбоустановку, кДж/ч; N_э –
электрическая мощность турбины, кВт;

,                                  (2.9)                                                                                                  

Q_пк – тепловая
нагрузка парового котла, кДж/ч

  .                                (2.10)                                               
                                      

Используя
(2.9), (2.10) получаем следующее выражение для теплоты сожженного топлива Q_с

  .                   (2.11)  

Подставляя
значение Q_с в выражение: , получаем

.                                         (2.12)

        Или  

;                                              
(2.13)                              

Значения Q_ту, Q_пк и Q_c могут быть рассчитаны по следующим
формулам:

Q_ту = 3600(N_э + DN_г + DN_м) + DQ_к  = 3600N_i + DQ_к,

где DN_г – потери
мощности в электрическом генераторе; DN_м – механические потери турбины; DQ_к – потери
теплоты в конденсаторе; N_i и N_э–
внутренняя и электрическая мощности турбины;

,                                             
(2.14)

где DQ_тр – потери
теплоты трубопроводами пара и воды между парогенератором и турбоустановкой;

,                                               
(2.15)

где DQ_пк – потери
теплоты в парогенераторе.

;   ;   .

Электрическая
мощность N_э турбины
равна

,                                         (2.16)

где h_oi, h_м, h_г, – КПД:
внутренний относительный турбины, механический турбины, механический
электрического генератора; N_а – мощность
турбины в идеальном процессе;

h_oэ –
относительный электрический КПД турбины (h_oэ = h_oе×h_г).

h_oе –
относительный эффективный КПД турбины (h_oе = h_oi×h_м).

Таким образом, абсолютный электрический КПД
турбоустановки

.                                      (2.17)

Или

,                                          
(2.18)

где h_t –
термический КПД брутто турбоустановки.

  и  – абсолютные КПД,
характеризуют преобразование теплоты в работу в цикле. h_oi, h_oе, h_oэ, h_м и h_г, а также h_пк и h_тр –
относительные КПД, характеризуют степень технического совершенства оборудования
ТЭС; h_oi –
характеризует совершенство проточной части турбины, входных и регулирующих
устройств, т. е. энергетические потери.

Таким
образом, КПД электростанции по производству электроэнергии (КЭС)  зависит от термического КПД цикла и
относительных КПД элементов оборудования: . Принимая: ; ; ; ; ; , получаем .

При
осуществлении технологического процесса часть энергии расходуется внутри ТЭС
(подготовка топлива, подача дутьевого воздуха, отвод дымовых газов, подача питательной
воды, конденсата и охлаждающей воды конденсаторов и др.) в размере 4¸6 %
электроэнергии или около 1,5¸2,5 %
затрачиваемой теплоты топлива.

Если
принять долю расхода электроэнергии на собственные нужды, то

.

2.4. Расход пара на КЭС

Расход D₀, кг/с,
пара на турбину КЭС определяется из условия энергетического баланса

.                                           (2.19)

Откуда

,     (2.20)

где
N_э –
электрическая мощность генератора, кВт;  и  – соответственно
адиабатное (располагаемое) и действительное теплопадение пара, кДж/кг; i₀, i_ка и i_к –
энтальпия свежего пара, конечная энтальпия пара при адиабатном и действительном
процессах расширения пара в турбине; h_м= 0,98¸0,99; h_г=0,98¸0,99 (h_м, h_г —
учитывают механические и электрические потери); (h_г= 0,97¸0,98 – при воздушном
охлаждении).

Внутренний
относительный КПД турбины равен

,                                         
(2.21)

где N_i и N_а –
внутренняя мощность при действительном рабочем процессе пара в турбине и
мощность в идеальном процессе, кВт.

 h_oi=0,80¸0,88, для
крупных  турбоагрегатов h_oi = 0,85¸0,9.

Удельный
расход пара d₀, г/кДж, с учетом (2.20) равен

.  (2.22)

Значения D₀, кг/ч и d₀, кг/(кВт×ч), равны

;

.                                              (2.23)

Для современных конденсационных
турбин d₀ =0,8 г/кДж; d₀ =3 кг/(кВт×ч).

2.5. Расходы тепла и топлива на КЭС

1.
Расходы тепла на турбоустановку Q_ту, кВт и q_ту равны

;

.                                        (2.24)

Отметим,
что удельный расход тепла q_ту – величина
обратная КПД. Так как , то  (безразмерная
величина).

Если N_э выразить в
кВт, Q_ту – в кДж/ч, то q_ту будет в
кДж/(кВт×ч):

;

 .

При h_ту = 0,44¸0,46, q_ту = 2,2¸2,3 или q_ту = 8100¸7800
кДж/(кВт×ч).

Тепловая
нагрузка парогенератора (парового котла) Q_пк и расход
тепла топлива на электростанции Q_c связаны
уравнением

.                                                     
(2.25)

При
этом нужно иметь в виду, что давление и температура перегретого пара после
котла p_пе и t_пе
соответственно на 1,0¸1,5 МПа и 5
°С выше, чем давление и температура свежего пара перед турбиной.

Удельный
расход тепла на электростанцию:

,

; ; , то ,   ,

где  – КПД электростанции.

2. Расход
топлива

Мерой
экономичности электростанции наряду с КПД h_с и удельным
расходом тепла q_с служит удельный расход условного топлива b_у=, г/кДж или г/(кВт×ч).

Общее
уравнение теплового баланса конденсационной электростанции

.                                              
(2.26)

Тепловую
экономичность станции принято оценивать расходом условного топлива с  МДж/кг = 29,309 кДж/г
(Q_усл=7000 ккал/кг).

Для
условного топлива уравнение теплового баланса имеет вид

,                                               
(2.27)

где B_у – расход
условного топлива, г/с.

Если B_у выражено в
г/с, то b_у в г/кДж:

.                                           
(2.28)

Если
B_у выражено в
кг/ч, то B_у×29,31h_с = 3600N_э и удельный
расход топлива равен, г/(кВт×ч)

                            
(2.29)

Таким
образом, удельный расход условного топлива обратно пропорционален КПД
электростанции и прямо пропорционален удельному расходу тепла, для значений   г/кДж или b_у=332¸375 г/(кВт×ч).

2.6. Процесс
работы пара в конденсационной турбине

без
регулируемого отбора пара в i, S–диаграмме.

Определение
расхода пара

Исходные данные:

  – мощность на зажимах генератора N_э, кВт;

  – рабочее число оборотов ротора турбины n,
об/мин;

      – начальные параметры пара:  давление перед стопорным  кла­паном p₀,
ата, температура  t₀
, °С;

      –давление 
отработанного   пара   или давление 
в   конденсаторе р_к, ата;

     
–давление отбираемого пара  р_отб,  ата,  и
его количество d_отб (для турбин с регулируемым
отбором пара, см. п. 2.8).

Тепловой расчет турбины начинают с
предварительного построения теплового процесса на i,S –диаграмме (рис. 2.4).

1. На диаграмме i,S
по параметрам р_{0 ,} t₀  наносят точку А₀ состояние пара перед стопорным клапаном).

2. Из точки А₀ проводят линию изоэнтропийного процесса до
пересечения с изобарой, соответствующей давлению отработанного пара р_к . Точку пересечения обозначают А_1t.

        3. Определяют разность энтальпий точек А₀ и A_1t

i₀
– i_1t=H₀,

т.е.
располагаемый теплоперепад на турбину без учета потери давления в стопорном  и регулирующих клапанах.

4. Потерю давления в стопорном и регулирующих
клапанах за счет дросселирования принимают 
Dp=(0,03÷0,05)р₀.    Обычно
берут Dp=0,05p₀,
тогда давление пара перед соплами регулирую­щей 
ступени  = 0,95р₀.
На  диаграмме i,S с помощью лекала проводят изобару, соответствующую
давлению .

5.
Проведя из точки А₀ линию постоянной энтальпии i=const
до пересечения с изобарой  намечают точку , соответствующую состоянию пара перед соплами регулирующей
ступени.

6. Потерю
давления в выхлопном патрубке (от последней ступени турбины    до  
конденсатора)    принимают  Dp_в.п.=(0,02 ÷ 0,08)р_к. Нижний предел берут для тур­бин, работающих с
противодав­лением, верхний – для конден­сационных турбин.

7. Определяют давление па­ра  на 
выходе   из  последней ступени p₂=p_к+Dp_в.п.  Изобару p₂
наносят  
на диаграмму i, S.                                                                    

8. Проведя  
из точки  ли­нию   изоэнтропийного процесса до пересечения с изобарой p₂, намечают точку  . Определяют
разность энтальпий в точках  и

,

т.е. изоэнтропийный теплоперепад в турбине с
учетом потерь в стопорном и регулирующих клапанах и выпускном патрубке.

9. По известному
значению внутреннего относительного КПД турбины  определяют
предполагаемый используемый теплоперепад 
H_i=H₀.

10. Откладывают от точки  (рис. 2.4.)
вниз по изоэнтропе используемый теплоперепад H_i и находят точку C. Проводя
через точку C линию параллельную оси S, до пересечения с изобарой p_2,
получают точку B,
характеризующую предполагаемое состояние пара после выхода из последней ступени
турбины. Соединив точки  и B
прямой линией определяют предполагаемый процесс в турбине. Продлив
горизонтальную линию от точки B до пересечения с
изобарой p_к,
получают точку B_к,
характеризующую состояние пара при входе в конденсатор или на выходе из патрубка
турбины, работающей с противодавлением.

11. Определяют секундный расход пара D₀, кг/с

.

Здесь – располагаемый теплоперепад, кДж/кг; – механический КПД турбины; – КПД редуктора; – механический КПД электрического генератора.

2.7. Расходы теплоты на ТЭЦ. КПД ТЭЦ

ТЭЦ отпускают потребителям электрическую энергию и
теплоту с паром, отработавшим в турбине. Принято распределять расходы теплоты
(и топлива) между этими двумя видами энергии.  

1. Расходы
теплоты на ТЭЦ и турбоустановку (ТУ) равны:

общий
расход теплоты на ТЭЦ (теплоты сожженного топлива)

;                                                        
(2.30)

общий расход
теплоты на ТУ

.                                                        
(2.31)

Индексы:
«с» – станция; «ту» – турбоустановка; «э» – электрическая энергия; «т» –
тепловая энергия (теплота).  и  – теплота топлива на
производство электрической и тепловой энергии.

,                                                        
(2.32)

где – тепловая нагрузка парового котла; – потери теплоты в котле.

Общий
расход теплоты на турбоустановку Q_ту ТЭЦ равен

,                                             
(2.33)

N_i –
внутренняя мощность турбины (без учета потерь в конденсаторе), кВт; DQ_к – потери
теплоты в конденсаторе;  Q_т – расход
теплоты на внешнего потребителя.

В
РФ принят физический метод распределения расхода теплоты между электрической и
тепловой энергией: на теплового потребителя относят фактический расход теплоты,
затрачиваемый на него, а на электроэнергию – остальное количество теплоты,
тогда

.                                       (2.34)

2.
Различают два вида КПД ТЭЦ и два вида КПД турбоустановки ТЭЦ:

а)
по производству (и отпуску) электрической энергии

;                                                     (2.35)

;                                                   
(2.36)

б)
по производству и отпуску теплоты

;                                                        
(2.37)

,                                                      
(2.38)

где  – затраты теплоты на
внешнего потребителя (теплового потребителя) с учетом h_т;  – отпуск теплоты
потребителю; h_т – КПД
отпуска теплоты, учитывает потери в паропроводах, сетевых подогревателях и др. h_т = 0,98¸0,99.

Для
ТЭЦ в целом с учетом КПД парового котла h_пк и КПД
транспорта теплоты h_тр получим:

;                                                 (2.39)

.                                                
(2.40)

Значение
 в основном
определяется значением , значение  – значением h_пк.

Выработка электроэнергии с использованием отработавшей
теплоты существенно повышает КПД по производству электроэнергии на ТЭЦ по
сравнению с КЭС и обусловливает экономию топлива.

2.8.
Процесс работы пара в турбине с регулируемым

 отбором пара в i, S –
диаграмме

Методика
построения теплового процесса на i, S – диаграмме в этом случае такая же, как и для турбин
без регулируемого отбора пара (см. п. 2.6 до п. 7 включительно). Исходные
данные приведены в п. 2.6. Дальнейшее построение процесса сводится к следующему.

1. Из точки  (рис. 2.5)
проводят линию изоэнтропийного процесса до пересечения с изобарой, соответствующей
давлению отбираемого пара р_отб.
Точку пересечения обозначают .

2.
Изоэнтропийный теплоперепад между точками  и  (), относящийся к части высокого давления (ЧВД) турбины,
умножают на ранее определенный η_oi и получают используемый
теплоперепад внутри ЧВД = η_0i.

Отложив
величину  вниз от точки  и проведя
горизонтальную линию до пересечения с изобарой р_отб, находят точку В‘,
характеризующую состояние пара в камере отбора.

3. Определяют потерю давления пара в регулирующих
клапанах части низкого давления (ЧНД) турбины Δр_отб=(0,03÷0,04) р_отб.

Потерю Δр_отб
наносят на диаграмму i, S и проводят
изобару р₁=р_отб – Δр_отб. Продлив горизонтальную
линию из точки В‘ до пересечения с
изобарой р₁, получают
точку , соответствующую состоянию пара перед соплами регулирующей
ступени ЧНД.

4. Из точки  проводят линию
изоэнтропийного процесса до пересечения с изобарой р₂ и намечают точку . Определяют разность энтальпий в точках   и .

,

т.е.
изоэнтропийный теплоперепад, приходящийся на ЧНД. Умножив Н«₀ на полученный ранее η_0i, получают
используемый теплоперепад внутри ЧНД.

.

 Отложив   вниз от точки  и проведя
горизонтальную линию до пересечения с изобарой р₂, находят точку В«,
характеризующую состояние пара после выхода из последней ступени ЧНД. Продлив
горизонтальную линию до пересечения с изобарой р_к, получают точку В_к,
характеризующую состояние пара при входе в конденсатор.

Для
определения расхода свежего пара на турбину с учетом его отбора необходимо
произвести расчет схемы регенерации (см. п. 4.7).

2.9. Расход пара на теплофикационную турбину

Расход
пара на теплофикационную (Т) турбину
(рис. 2.6 а) определяют путем сравнения с расходом пара на конденсационную (К) турбину с такими же параметрами пара.
Действительный расход пара К–турбины

.                           
             (2.41)

При
отборе пара из турбины в количестве D_т внутренняя
мощность ее снижается на величину . Здесь – количество пара отбираемого из турбины на теплофикацию;  i_т и i_к –
энтальпия пара в отборе и на входе в конденсатор.

Для
восстановления мощности турбины до первоначальной N_э необходимо
увеличить расход свежего пара в количестве DD₀

.

        Тогда дополнительный расход пара равен

,                                                (2.42)

где  – коэффициент
недовыработки мощности паром теплофикационного отбора. Следовательно расход
пара на турбину с отбором D_т и конденсацией
(на теплофикационную турбину)  равен

.                                                  
(2.43)

Коэффициент недовыработки
мощности Y_т есть относительное
увеличение расхода пара на турбину на единицу количества отбираемого пара
(характеризует долю недоработанного теплоперепада пара, идущего в отбор, см.
рис. 2.6).

0 £ Y_т £ 1, причем Y_т = 0 при i_т = i_к, Y_т = 1 при i_т = i₀. Обычно Y_т = 0,3¸0,7, в среднем Y_т = 0,5. Если D_т = 0, то D₀ = D_0(к).

Уравнение (2.43) выражает
энергетический баланс турбины, связь между расходом пара и электрической мощностью
турбины.

Уравнение материального баланса Т-турбины имеет вид

  ,                                                  
(2.44)                    

где
D_к – пропуск пара в
конденсатор, он меньше, чем D_0(к).

и 

                                                        
.                                             
(2.45)                                   

где
– уменьшение расхода пара в конденсаторе.

Баланс мощностей в турбине с
конденсацией пара и отбором  (в теплофикационной
турбине) выражается уравнениями

и

,

где N_вд, N_нд и N_т, N_к – мощность развиваемая ЧВД
и ЧНД турбины и пара, идущего в отбор и через всю турбину в конденсатор (D_вд = D₀; D_нд = D_к).

Турбина с противодавлением (типа Р)

Общий тепловой баланс
теплофикационной турбины с противодавлением (рис. 2.6 б).

.                                                    
(2.46)

Выработка электроэнергии для турбины с противодавлением  непосредственно
зависит от пропуска пара через нее D_т  (расхода пара на теплового потребителя D_т=D₀).

.                                       (2.47)

Зависимость
 от  D_т  для турбин с противодавлением ограничивает их
применение на ТЭЦ. Возможное уменьшение потребления пара D_т не
позволяет обеспечивать выработку необходимой электрической мощности. Требуемая
при этом дополнительная мощность усложняет всю установку.

Расходы
теплоты и пара на теплового потребителя связаны уравнением

,                                                       
(2.48)                         

где i_ок –
энтальпия обратного конденсата (считаем, что невозврата конденсата от потребителя
в количестве D_т нет).

Подставляя
в энергетическое уравнение (2.47) турбины с противодавлением вместо D₀ величину D_т из (2.48),
получим

,                                             
(2.49)

где Q_т – расход теплоты
на тепловом потреблении, ГДж/ч.

Удельная
выработка электроэнергии на тепловом потреблении кВт×ч/ГДж равна

 .                                           
(2.50)

 = 50¸100 кВт×ч/ГДж. Этот
показатель применим и для потока пара отбора в турбине с отбором и
конденсацией.

2.10. Тепловая экономичность и расход топлива на
ТЭЦ

Процессы
производства и отпуска электроэнергии и теплоты характеризуются КПД ТЭЦ по
отпуску электрической энергии и теплоты.

;

,                                               
(2.51)

где N_э –
электрическая мощность турбины;  – отпуск теплоты
потребителю.

       Процесс совместного производства
электроэнергии и теплоты характеризуют полным КПД ТЭЦ

.                                                
(2.52)

Для
теплофикационной турбины соответственно получим

,                                                
(2.53)

где Q_ту – общий
расход теплоты на ТУ.

Обозначим долю теплоты, затрачиваемой в турбине на
внешнего потребителя, через b_т:

;

.                                            
(2.54)

Абсолютный
электрический КПД турбины равен

.                                                    
(2.55)

Найдем
соотношение между полным и абсолютным КПД турбины и КПД турбины по отпуску
электроэнергии :

                                       (2.56)

Общее
соотношение между этими тремя КПД

.                                               
(2.57)

Если
известны b_т и один из
КПД, другие два определяются из (2.57).

Посредством
коэффициента b_т  расходы теплоты для ТЭЦ рассчитываются следующим
образом.

а) теплота
топлива на производство тепловой энергии

;                                                           
(2.58)

б) теплота
топлива на производство электрической энергии

.                                                        (2.59)

Аналогично,
расходы топлива

;

,                                           
(2.60)

где B = B_э + B_т – общий
расход топлива на ТЭЦ.

Расходы
топлива связаны с КПД следующими соотношениями:

;

.                                                
(2.61)

Общий
расход топлива на ТЭЦ можно рассчитать из уравнения теплового баланса котла
(без промперегрева):

.                                   (2.62)

Удельный
расход условного топлива на единицу производимой электроэнергии  ( МДж/кг).

Для
конденсационного режима  и тогда  г/(кВт×ч).

Для  турбины с противодавлением    , получим   г/(кВт×ч).

Удельный
расход условного топлива на единицу отпущенной теплоты

 при   кг/ГДж.

2.11. Сравнение КПД теплофикационной и
конденсационной турбин

Отношение
КПД по производству электроэнергии турбины с отборами (типа КО)  к КПД по производству
электроэнергии чисто конденсационной турбины  равно [4].

.                                           
(2.63)

Здесь А_т = N_т/N_к –
энергетический коэффициент пара отбора, равный отношению мощности пара отбора N_т и пара конденсационного
потока N_к.

Относительное повышение КПД теплофикационной турбины по
производству электроэнергии по сравнению с КПД конденсационной турбоустановки
равно

.                                              
(2.64)

При  любом  отборе пара  > 0. Например, если
N_т = N_к и А_т = 1, а также  » 0,5, то  = 0,33. При больших значения
А_т (N_т > N_к и А_т > 1) относительное
повышение КПД еще больше.

2.12. Сравнение комбинированного и раздельного производства

электрической
и тепловой энергии

Комбинированное
производство электрической и тепловой энергии обеспечивает уменьшение расхода
топлива. Однако при малой годовой продолжительности теплового потребления и дешевом
топливе экономичным может быть раздельное производство электрической энергии и
теплоты. Это когда, электроэнергия вырабатывается конденсационным путем, а
теплота отпускается из котельной низкого давления (КНД) (рис. 2.7).

Сравним
расходы топлива (основные технико-экономические показатели) на ТЭЦ и раздельную
установку (РУ). Общие расходы топлива на раздельную установку  и на ТЭЦ  равны:

В_ру=В_КЭС + В_КНД;                                           
(2.65)

Втэц=В_э + В_т
.                                              (2.66)                                          

Или,
выражая  и через удельные расходы топлива, получим

В_ру=b_КЭС(N_к + N_т) + В_КНД;                                        (2.67)

 .                                        (2.68)

        Здесь – соответственно мощность пара идущего в отбор и через всю
турбину в конденсатор;

– удельный расход
топлива, связанный с паром отбора;

 и принимая , получаем

;                                              
(2.69)

(индекс «р» означает противодавление).        

Соотношение
(2.69) позволяет определить экономию топлива благодаря теплофикации. Заменяя в
(2.69)  (N_т – мощность
пара отбора на теплофикацию,  – удельная выработка
электроэнергии на тепловом потреблении), получаем удельную экономию условного
топлива, кг/ГДж:

,                             
(2.70)

или

.                                                 
(2.71)

Принимая
=50¸100 кВт×ч/ГДж,
получаем Db=7,5¸22,5
кг/ГДж, в среднем Db=15
кг/ГДж). Формула (2.71) наглядно показывает зависимость эффективности
теплофикации от энергетического совершенства выработки электроэнергии на тепловом
потреблении, т.е. от параметров пара и КПД турбины и ТЭЦ. При отпуске теплоты Q_т=1 млн. ГДж
экономия условного топлива за счет теплофикации DВ»15000 т.

Глава вторая

ЭНЕРГЕТИЧЕСКИЕ ПОКАЗАТЕЛИ КОНДЕНСАЦИОННОЙ ЭЛЕКТРОСТАНЦИИ

2.1. Основной энергетический показатель электростанции

Основным показателем энергетической эффективности
электростанции является коэффициент полезного действия (КПД) по отпуску
электрической энергии, называемый абсолютным электрическим коэффициентом
полезного действия электростанции, Он определяется отношением отпущенной
(производственной, выработанной) электроэнергии к затраченной энергии (теплоте
сожженного топлива).

КПД
электростанции по отпуску электроэнергии называется КПД нетто:

где Э — выработка электроэнергии; Э_с.н
— расход электроэнергии на собственные нужды ТЭС;  — доля
расхода электроэнергии на собственные нужды, равная в зависимости от параметров
пара и вида топлива 4–6%; Q_c —
теплота, затраченная в топливе. Значения Э, Э_с.н, Q_c относятся к любому
промежутку времени и выражены в одинаковых электрических или тепловых единицах.

Важным
расчетным показателем является КПД, определяемый для часового промежутка
времени:

где N_э — электрическая
мощность, кВт; Q_c —
теплота сожженного топлива, кДж/ч.

При
решении реальных задач энергетического хозяйства, при его планировании и в
отчетности используют КПД нетто, в общем анализе энергетической эффективности
электростанции — КПД брутто, которым определяют энергетическую
эффективность электростанции в первом приближении:

Для
часового промежутка времени КПД брутто

где Q_c — в
кДж/ч.

КПД
брутто определяет эффективность процесса выработки электроэнергии на
электростанции.

КПД брутто и нетто электростанции связаны между собой
отношением

.

Энергетический
процесс современной паротурбинной электростанции основан на термодинамическом
цикле Ренкина с подводом и отводом теплоты рабочему телу (воде и водяному пару)
при постоянном давлении. Термический КПД этого цикла для 1 кг рабочего
тела

где Q₀ и Q_к — подвод и отвод теплоты в этом цикле; h₀ и h_к.а — энтальпия пара
перед турбиной и после нее при адиабатном расширении; h¢_к и h_п.н — энтальпии конденсата пара после турбины и питательной
воды после питательного насоса; принято h_п.н = h_п.в, т. е. что
питательная вода после насоса поступает в паровой котел.

Равенство
(2.5) можно записать в виде

Здесь Н_а
— располагаемый теплоперепад в адиабатном процессе работы пара в турбине; H_н.а — работа повышения давления воды в питательном насосе,
эквивалентная подогреву воды в адиабатном процессе t_н.а = H_н.а; Q¢₀ = h₀ –h¢_к — расход теплоты на турбину без учета подогрева воды в питательном
насосе, кДж/кг.

Формулы
(2.5) и (2.6) определяют КПД нетто с учетом работы питательного насоса

где u— усредненный
удельный объем воды на входе и выходе, м³/т; p_н и p_в — давление воды на
выходе из насоса и входе в насос, МПа.

КПД
брутто цикла Ренкина без учета подогрева воды в питательном насосе

Теплоперепад
H_а расходуется на
производство электроэнергии и приводные двигатели собственных нужд. Расход
энергии на питательный насос — основная составляющая общего собственного
расхода энергии на электростанции. Мощность, потребляемая питательным насосом,
зависит непосредственно от начального давления пара p₀ и должна обязательно учитываться при выборе начальных
параметров пара на электростанции. Так, при u = 1,1 м³/т и p_н – p_в = 30 МПа
t_н.а = H_н.а = 33 кДж/кг.

2.2. Основные
составляющие абсолютного КПД электростанции

Коэффициент полезного действия электростанции по
производству электроэнергии зависит от КПД основных элементов — турбоустановки
и парового котла, а также соединяющих их трубопроводов пара и воды (рис. 2.1).

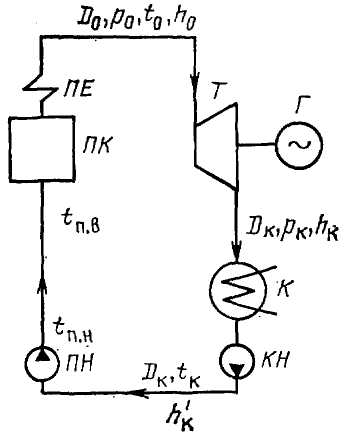
Рис. 2.1. Тепловая схема простейшей конденсационной электростанции:
ПК— паровой котел; ПЕ — пароперегреватель;
Т — турбина; Г — электрический генератор; К— конденсатор;
КН — конденсатный насос; ПН — питательный насос

Абсолютный
электрический КПД турбоустановки

где Q_ту — расход теплоты
на турбоустановку, кДж/ч.

КПД
парового котла

,

где Q_п.к —
тепловая нагрузка парового котла, кДж/ч.

КПД транспорта теплоты (трубопроводов) определяется
выражением

.

Используя
последние соотношения, получаем следующее выражение для теплоты сожженного
топлива:

.

Подставляя
выражение для Q_c в
(2.4), получаем

,

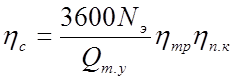
или

Общий
баланс теплоты конденсационной электростанции (энергоблока) выражается
следующим образом.

Наиболее представительным показателем энергоэффективности ТЭЦ может служить общий энергетический КПД станции и определяемый на его основе удельный расход топлива на отпущенную энергию, как электрическую, так и тепловую, определенные в одной единице измерения. Тогда величина последнего может быть определена как:

где Эотп — величина отпуска электроэнергии от ТЭЦ; Q_ОТП, — величина отпуска тепловой энергии от ТЭЦ; b^ТЭЦ_ТЭ — удельный расход на отпуск тепловой энергии от ТЭЦ; к_э — коэффициент, переводящий тепловую энергию в электрическую (1кВт-ч = 3600 кДж).

Пример. Предположим, что b^тэц_ээ = 0,24 кг у.т./кВт-ч, b^тэц_тэ = 165 кг у.т./Гкал, Э_отп ⁼ 600 млнкВт-ч, Q_0Tn = 700 тыс.Гкал, к_э = 1/3600 кВт-ч/кДж = 1/860 кВт-ч/ккал. Тогда:

Это эквивалентно 0,123 : 0,183 = 0,67 (67 % КПД).
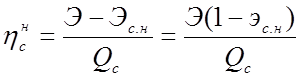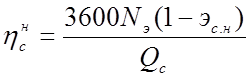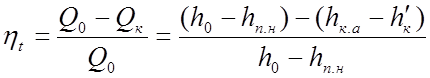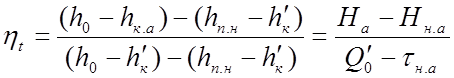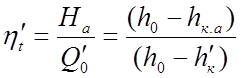