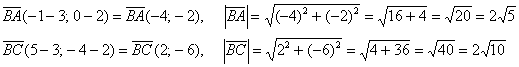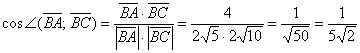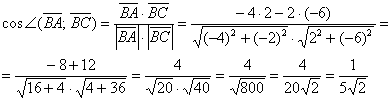Как найти косинус зная координаты вершин - Avtoru.top

Косинус угла между векторами

Формула

Чтобы найти косинус угла между векторами нужно найти отношение скалярного произведения векторов и произведение их длин (модулей). Если векторы заданы на плоскости двумя координатами $ overline{a}=(x_1;y_1) $ и $ overline{b}=(x_2;y_2) $, то косинус угла между ними вычисляется по формуле:

$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}|cdot |overline{b}|} = frac{x_1 x_2 + y_1 y_2}{sqrt{x_1 ^2 + y_1 ^2}cdot sqrt{x_2 ^2 + y_2 ^2}} $$

Если векторы будут заданы тремя координатами $ overline{a}=(x_1;y_1;z_1) $ и $ overline{b}=(x_2;y_2;z_2) $, то есть в пространстве, то нахождение косинуса угла между векторами нужно выполнить по формуле:

$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}|cdot |overline{b}|} = frac{x_1 x_2 + y_1 y_2 + z_1 z_2}{sqrt{x_1 ^2 + y_1 ^2 +z_1 ^2}cdot sqrt{x_2 ^2 + y_2 ^2 + z_2 ^2}} $$

В числителе находится скалярное произведение векторов, то есть каждая координата умножается на соответствующую координату другого вектора и при этом находится сумма всех произведений. А в знаменателе расположено произведение модулей векторов. Каждый модуль равен извлеченному квадратному корню из суммы квадратов координат вектора.

Примеры решений

Пример

Даны два вектора $ overline{a} =(3;1) $ и $ overline{b} = (2;4) $. Требуется найти косинус угла между векторами.

Решение

Напомним как найти косинус угла между векторами. Необходимо определить на плоскости или в пространстве находятся векторы, то есть сколько у них координат. Затем воспользоваться подходящей формулой.

Первым делом вычисляем скалярное произведение: каждую координату одного вектора умножаем на соответствующую координату другого вектора, а потом суммируем произведения:

$$ (overline{a},overline{b}) = 3cdot 2 + 1 cdot 4 = 6+4=10 $$

Далее находим чему равны модули каждого из векторов:

$$ |overline{a}|=sqrt{3^2+1^2} = sqrt{10} $$

$$ |overline{b}|=sqrt{2^2+4^2} = sqrt{4+16} = sqrt{20} $$

Теперь можно найти косинус угла между векторами подставив найденные значения в первую формулу:

$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}|cdot |overline{b}|} = frac{10}{sqrt{10}cdot sqrt{20}} = $$

$$ = frac{10}{sqrt{200}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2} $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ cos phi = frac{sqrt{2}}{2} $$

Источник

Угол между векторами

Определение

Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.

Угол между векторами

На изображении это α, который также можно обозначить следующим образом:

(left(widehat{overrightarrow a;overrightarrow b}right))

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как и любой другой угол, векторный может быть представлен в нескольких вариациях.

Острый:

Острый угол между векторами

Тупой:

Тупой угол между векторами

Прямой:

Прямой угол

С величиной (0^circ) (то есть, векторы сонаправлены):

0 градусов

С величиной (180^circ) (векторы направлены в противоположные стороны):

180 градусов

Нахождение угла между векторами

Как правило, угол между ( overrightarrow a) и (overrightarrow b) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.

Определение

Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.

Формула скалярного произведения:

(left(overrightarrow a;overrightarrow bright)=left|overrightarrow aright|timesleft|overrightarrow bright|timescosleft(widehat{overrightarrow a;overrightarrow b}right))

Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
Если векторы имеют общую направленность, то есть угол между ними равен (0^circ), а косинус — 1, то СП будет тоже положительным.
Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
Если α равен (180^circ), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
Если α — прямой, то СП равно 0, так как косинус (90^circ) равен 0.

В случае, если overrightarrow a и overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})

Расчет угла, если вектор задан координатами

В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде (overrightarrow a=left(a_x;a_yright)) и (overrightarrow b=left(b_x;b_yright)), то угол между ними можно найти следующим образом:

Если же координаты находятся в трехмерном пространстве и заданы в виде:

(overrightarrow a=left(a_x;a_y;a_zright))

( overrightarrow b=left(b_x;b_y;b_zright))

то формула принимает такой вид:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})

Расчет угла, если заданы три точки в прямоугольной системе координат

В этом случае проще будет разобраться с объяснениями сразу на примере.

Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между (overrightarrow{AC}) и (overrightarrow{BC}).

Решение

Для начала найдем их координаты по известным координатам заданных точек:

(overrightarrow{AC}=(6-3, -1-(-2))=(3,1))

(overrightarrow{BC}=(6-2, -1-1)=(4,-2))

После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:

(cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac{(overrightarrow{AC};;overrightarrow{BC})}{left|overrightarrow{AC}right|cdotleft|overrightarrow{BC}right|}=frac{3cdot4+1cdot(-2)}{sqrt{3^2+1^2}cdotsqrt{4^2+{(-2)}^2}}=frac{10}{sqrt{10}cdot2sqrt5}=frac{10}{10sqrt2}=frac1{sqrt2})

Ответ: (cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac1{sqrt2}.)

Примеры решения задач

Для наглядности, взглянем на примеры решения задач по данной теме.

Задача 1

Известно, что (overrightarrow a) и (overrightarrow b). Их длины равны 3 и 6 соответственно, а скалярное произведение равно -9. Нужно найти cos угла между векторами и его величину.

Решение

Применим формулу:

( cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})

Подставим известные значения:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{-9}{3cdot6}=-frac12)

Далее найдем угол между данными векторами:

(arccosleft(-frac12right)=frac{3pi}4)

Ответ: (left(widehat{overrightarrow a;overrightarrow b}right)=-frac12,;left(widehat{overrightarrow a;overrightarrow b}right)=frac{3pi}4.)

Задача 2

В пространстве даны координаты (overrightarrow a=(8; -11; 7)) и (overrightarrow b=(-2; -7; 8)). Вычислить угол α между ними.

Решение

Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:

Подставляем значения и получаем:

(cosleft(alpharight)=frac{8cdot(-2)+(-11)cdot(-7)+7cdot8}{sqrt{8^2+{(-11)}^2+7^2}cdotsqrt{{(-2)}^2+{(-7)}^2+8^2}}=frac{117}{sqrt{234}cdotsqrt{117}}=frac{sqrt{117}}{sqrt{234}}=frac1{sqrt2}=frac2{sqrt2})

Теперь находим угол α:

(alpha=arccosleft(frac2{sqrt2}right)=45^circ)

Ответ: (45^circ).

Задача 3

Известны (overrightarrow a=(3; 4)) и (overrightarrow b=(2; 5)). Найти угол между ними.

Решение

Для расчета используем формулу:

Подставим известные значения и получим:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}}=frac{3cdot2+4cdot5}{sqrt{3^2+4^2}cdotsqrt{2^2+5^2}}=frac{26}{sqrt{25}cdotsqrt{29}}=frac{26}{5sqrt{29}})

Ответ: (cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{26}{5sqrt{29}})

Источник

Мы уже находили косинусы углов треугольника по его сторонам в произвольном треугольнике и косинус острого угла прямоугольного треугольника.

Рассмотрим, как найти косинусы углов треугольника по его вершинам.

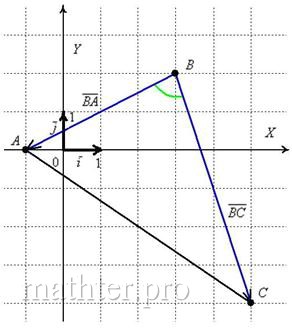
Задача

Дано: ΔABC,

A(-2;0), B(6;1), C(-3;-5).

1) Найти косинусы углов треугольника ABC;

2) Определить вид треугольника.

Решение:

1) Угол A образован векторами

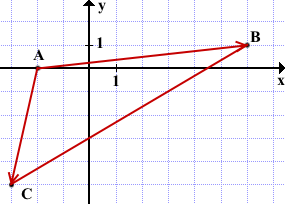
(Чертёж не обязательно делать на координатной плоскости. Достаточно выполнить его схематически, для упрощения понимания, какой угол какими векторами образован).

Следовательно,

$[cos A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}}.]$

Найдём координаты векторов:

$[overrightarrow {AB} (x_B - x_A ;y_B - y_A ),]$

$[overrightarrow {AC} (x_C - x_A ;y_C - y_A ),]$

Находим скалярное произведение векторов:

Поскольку скалярное произведение меньше нуля, угол, образованный данными векторами, тупой. Значит треугольник ABC — тупоугольный.

Длины (или модули) векторов:

$[left| {overrightarrow {AB} } right| = sqrt {8^2 + 1^2 } = sqrt {65} ,]$

$[left| {overrightarrow {AC} } right| = sqrt {( - 1)^2 + ( - 5)^2 } = sqrt {26} .]$

Отсюда

$[cos A = frac{{ - 13}}{{sqrt {65} cdot sqrt {26} }} = frac{{ - 13}}{{sqrt {5 cdot 13 cdot 2 cdot 13} }} = ]$

$[= frac{{ - 13}}{{13sqrt {10} }} = - frac{1}{{sqrt {10} }} = - frac{{sqrt {10} }}{{10}}.]$

2) Угол B образован векторами

Таким образом,

$[cos B = frac{{overrightarrow {BA} cdot overrightarrow {BC} }}{{left| {overrightarrow {BA} } right| cdot left| {overrightarrow {BC} } right|}}.]$

Так как

— противоположные векторы, то их координаты отличаются только знаками и векторы имеют одинаковую длину:

$[overrightarrow {BC} (x_C - x_B ;y_C - y_B ),]$

$[left| {overrightarrow {BC} } right| = sqrt {( - 9)^2 + ( - 6)^2 } = sqrt {117} .]$

$[cos B = frac{{78}}{{sqrt {65} cdot sqrt {117} }} = frac{{13 cdot 6}}{{sqrt {5 cdot 13 cdot 9 cdot 13} }} =]$

$[= frac{{13 cdot 6}}{{13 cdot 3sqrt 5 }} = frac{2}{{sqrt 5 }} = frac{{2sqrt 5 }}{5}.]$

3) Угол C образован векторами

$[cos C = frac{{overrightarrow {CA} cdot overrightarrow {CB} }}{{left| {overrightarrow {CA} } right| cdot left| {overrightarrow {CB} } right|}}.]$

$[cos C = frac{{39}}{{sqrt {26} cdot sqrt {117} }} = frac{{13 cdot 3}}{{sqrt {2 cdot 13 cdot 9 cdot 13} }} = ]$

$[= frac{{13 cdot 3}}{{13 cdot 3sqrt 2 }} = frac{1}{{sqrt 2 }} = frac{{sqrt 2 }}{2}.]$

Ответ:

$[cos A = - frac{{sqrt {10} }}{{10}},cos B = frac{{2sqrt 5 }}{5},cos C = frac{{sqrt 2 }}{2};]$

ΔABC — тупоугольный.

Источник

1.6.9. Как найти угол между векторами в координатах?

Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса

угла между векторами выразить через

координаты векторов :

Косинус угла между векторами плоскости и ,

заданными в ортонормированном базисе , выражается формулой:
.

Косинус угла между векторами пространства , заданными в ортонормированном базисе , выражается формулой:

Возвращаемся к нашим треугольникам:

Задача 31

Даны три вершины треугольника . Найти .

Решение: по условию чертёж выполнять не требуется, но всё-таки:

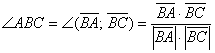
Из чертежа совершенно очевидно, что угол треугольника совпадает с углом между векторами и , иными словами: , и дальнейшее понятно. Найдём векторы и их длины:

Вычислим скалярное произведение:

Таким образом:

Именно такой порядок выполнения задания рекомендую «чайникам». Более подготовленные читатели могут записать вычисления

«одной строкой»:

Косинус получился «плохим» (не табличным), однако, это не окончательный ответ задачи, и поэтому, к слову, не имеет особого

смысла избавляться от корня в знаменателе.

Найдём сам угол:

Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки можно использовать Алгебраический

Калькулятор (см. Приложения) или даже измерить угол транспортиром (у кого он есть). Только не

повредите покрытие монитора =)

Ответ:
В ответе не забываем, что спрашивалось про угол треугольника (а не про угол между векторами), не забываем

указать точный ответ: и приближенное значение

угла: , найденное с помощью

калькулятора.

Задача 32

В пространстве задан треугольник координатами своих вершин , .

Найти угол между сторонами и

Это пример для самостоятельного решения, и, конечно же, задачка творческая, повторяем взаимосвязь между углом и знаком скалярного произведения:

Задача 33

При каком значении угол между векторами будет: а) острым, б) прямым, в) тупым?

Решение и ответ в конце книги.

Следующий небольшой параграф будет посвящен ортогональным проекциям векторов, в которых тоже «замешано» скалярное произведение:

1.7.1. Как найти проекцию вектора на вектор?

1.6.8. Если векторы заданы суммами векторов с известными координатами

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Содержание:

Формула
Примеры вычисления косинуса угла между векторами

Формула

Чтобы найти косинус угла между векторами нужно,
скалярное произведение этих векторов
разделить на произведение их длин.

В случае если векторы заданны на плоскости и имеют координаты $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, то косинус между ними вычисляется по формуле:

$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}}}$$

Если же векторы заданы в пространстве, то есть
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то косинус угла вычисляется по формуле

$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$

Примеры вычисления косинуса угла между векторами

Пример

Задание. Найти косинус угла $phi$ между векторами
$bar{a}=(4 ;-3)$ и $bar{b}=(1 ;-2)$

Решение. Так как векторы заданы на плоскости, воспользуемся формулой

$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}}}$

Подставим координаты заданных векторов:

$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{4 cdot 1+(-3) cdot(-2)}{sqrt{4^{2}+(-3)^{2}} sqrt{1^{2}+(-2)^{2}}}=$$
$$=frac{4+6}{sqrt{16+9} sqrt{1+4}}=frac{10}{sqrt{25} sqrt{5}}=frac{10}{5 sqrt{5}}=frac{2 sqrt{5}}{5}$$

Ответ. $cos phi=frac{2 sqrt{5}}{5}$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти косинус угла между векторами
$bar{a}=(3 ;-4 ; 0)$ и $bar{b}=(4 ;-4 ;-2)$, заданных в пространстве.

Решение. Для нахождения косинуса угла между заданными векторами, воспользуемся формулой

$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} cdot sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$

Подставляя координаты векторов $bar{a}$ и $bar{b}$, получим

$$begin{aligned} cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{3 cdot 4+(-4) cdot(-4)+0 cdot(-2)}{sqrt{3^{2}+(-4)^{2}+0^{2}} sqrt{4^{2}+(-4)^{2}+(-2)^{2}}} &=\=frac{12+16+0}{sqrt{9+16+0} sqrt{16+16+4}}=frac{28}{sqrt{25} sqrt{36}}=frac{28}{5 cdot 6}=frac{14}{15} end{aligned}$$

Ответ. $begin{aligned} cos phi=frac{14}{15} end{aligned}$

Читать дальше: как найти скалярное произведение векторов.

Источник

Косинус угла между векторами

Формула

Примеры решений

Угол между векторами

Нахождение угла между векторами

Расчет угла, если вектор задан координатами

Расчет угла, если заданы три точки в прямоугольной системе координат

Примеры решения задач

Задача 1

Задача 2

Задача 3

1.6.9. Как найти угол между векторами в координатах?

Формула

Примеры вычисления косинуса угла между векторами

Не пропустите также: