Как найти косинус угла в тупом треугольнике

Теорема косинусов

Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.

  • a² = b² + c² – 2b.c.cosα
  • b² = a² + c² – 2a.c.cosβ
  • c² = a² + b² – 2a.b.cosγ

Например:

Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.

Решение по формуле a² = b² + c² – 2b.c.cosα:

cos α = cos 120º = — 1/2 (это значение можно найти в таблицах)

a² = 12² + 8² – 2×12×8×(- 1/2)

Длина третьей стороны — примерно 17,436 см.

Следствия

Следствие косинуса угла треугольника

При помощи теоремы косинусов можно найти косинус угла треугольника.

Используйте теорему косинусов, чтобы найти угол β.

Решение:

Будем использовать эту версию формулы:

cos β = (6² + 8² − 7²) / 2×6×8

Следствие верхней части формулы cos α

Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):

  • b²+c²−a² 0, значит угол α — острый.

Доказательство теоремы косинусов

Нужно доказать, что c² = a² + b² − 2a.b.cos C

1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a CD = a.cos C.

2. Вычитаем это из стороны b, так мы получим DA:

3. Мы знаем из определения синуса, что в том же треугольнике BCD:

sin C = BD/a BD = a.sinC.

4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²

5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²

6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C

6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC

7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC

8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C

Теорема косинусов для равнобедренного треугольника

В равнобедренном треугольнике:

  • две его стороны равны;
  • углы при основании равны.

Используем формулу теоремы косинусов

a² = b² + c² – 2b.c.cosα

Подставляем все известные:

x² = 8² + 8² – 2×8×8×cos140º

x² = 64 + 64 – 128 × (-0,766)

Теорема синусов

Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:

Теорема косинусов и синусов

О чем эта статья:

Формулировка и доказательство теоремы косинусов

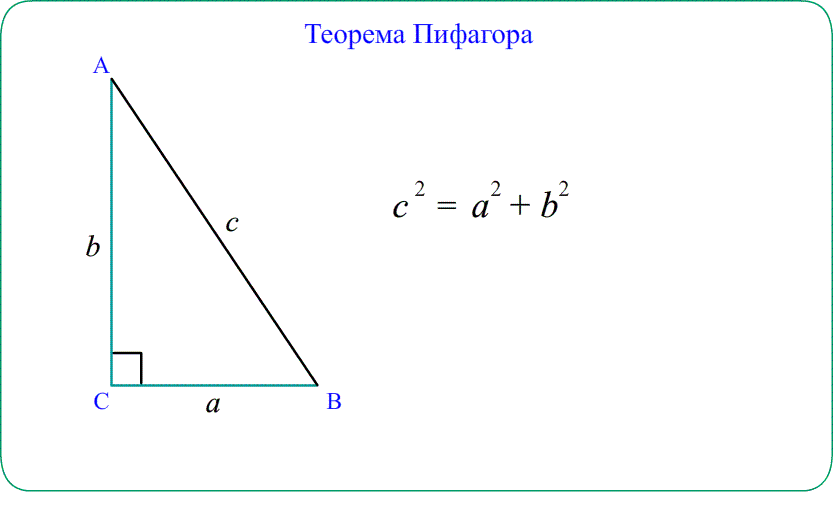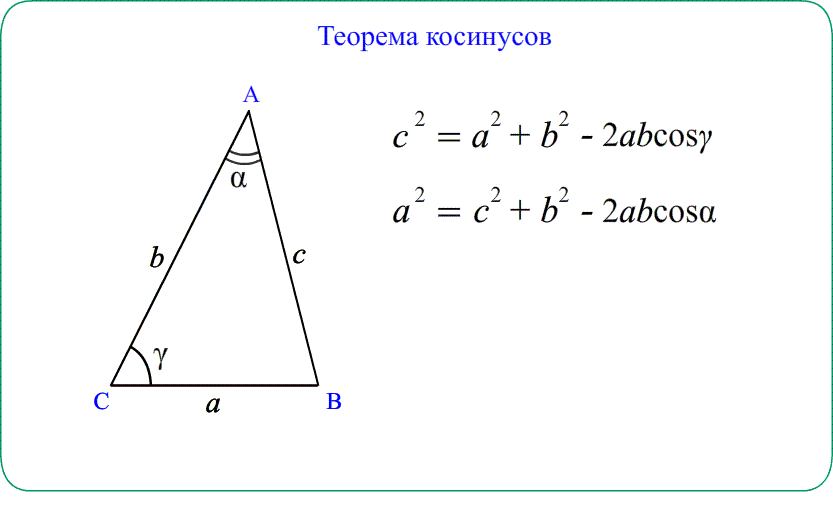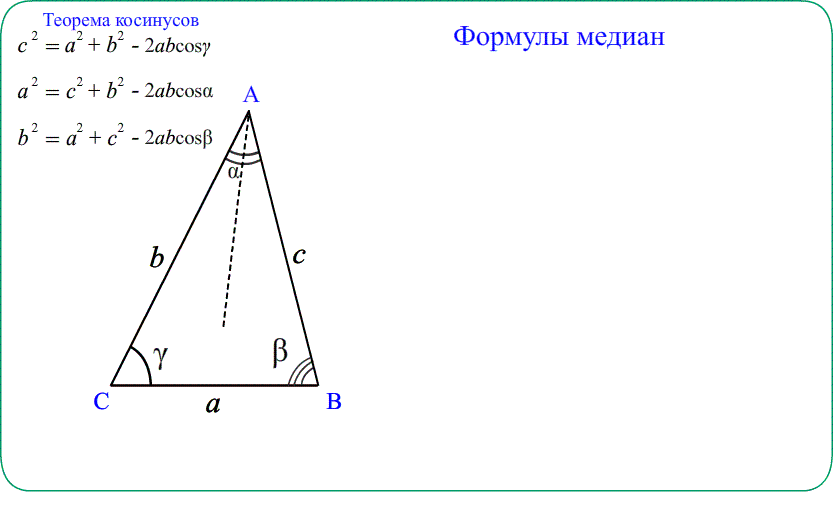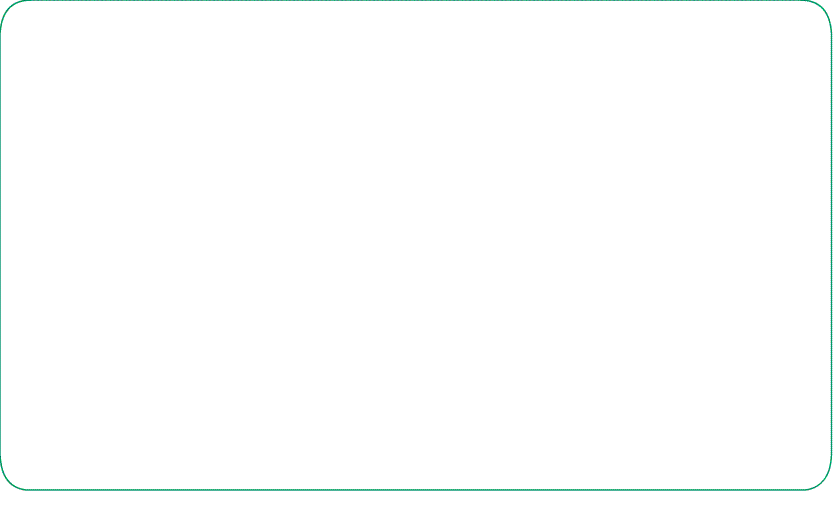
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a 2 = b 2 + c 2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

  • Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
  • Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
  • Когда b 2 + c 2 — a 2

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

  • AD = b × cos α,
  • DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

  • h 2 = b 2 — (b × cos α) 2
  • h 2 = a 2 — (c – b × cos α) 2

Приравниваем правые части уравнений:

  • b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2
  • a 2 = b 2 + c 2 — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

  • b 2 = a 2 + c 2 — 2ac × cos β;
  • c 2 = a 2 + b 2 — 2ab × cos γ.

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a 2 = b 2 + c 2 — 2bc cos α

b 2 = c 2 + a 2 — 2ca cos β

c 2 = a 2 + b 2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

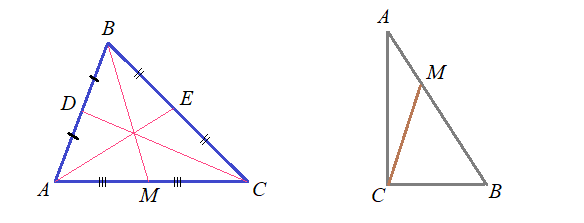
Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

    Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
    Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.

  • Если c 2 2 + b 2 , то ∠C — острый.


Теорема косинусов. Доказательство теоремы косинусов.

Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.

Теорема косинусов:

Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:

Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Следствие из теоремы косинусов.

  • Теорема косинусов используется для определения cos угла треугольника:

h 2 = a 2 — (c – b cos α) 2 (2)

Приравниваем правые части уравнений (1) и (2):

b 2 — (b cos α) 2 = a 2 — (c — b cos α) 2

a 2 = b 2 + c 2 — 2bc cos α.

Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определить стороны b и c:

источники:

http://skysmart.ru/articles/mathematic/teorema-kosinusov-i-sinusov

http://www.calc.ru/Teorema-Kosinusov-Dokazatelstvo-Teoremy-Kosinusov.html

Источник

Как найти косинус угла

Косинус – одна из основных тригонометрических функций. Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе. Определение косинуса привязано к прямоугольному треугольнику, но зачастую угол, косинус которого необходимо определить, в прямоугольном треугольнике не расположен. Как найти значение косинуса любого угла?

Как найти косинус угла

Инструкция

Если необходимо найти косинус угла в прямоугольном треугольнике, необходимо воспользоваться определением косинуса и найти отношение прилежащего катета к гипотенузе:
cos? = a/c, где а – длина катета, с – длина гипотенузы.

Если необходимо найти косинус угла в произвольном треугольнике, необходимо воспользоваться теоремой косинусов:
если угол острый: cos? = (a2 + b2 – c2)/(2ab);
если угол тупой: cos? = (с2 – a2 – b2)/(2ab), где а, b – длины сторон прилежащих к углу, с – длина стороны противолежащей углу.

Если необходимо найти косинус угла в произвольной геометрической фигуре, необходимо определить величину угла в градусах или радианах, а косинус угла найти по его величине с помощью инженерного калькулятора, таблиц Брадиса или любого другого математического приложения.

Полезный совет

Математическое обозначение косинуса – cos.
Значение косинуса не может быть больше 1 и меньше -1.

Источники:

  • как вычислить косинус угла
  • Тригонометрические функции на единичной окружности

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Для нахождения элементов в произвольном треугольнике используется теорема синусов или теорема косинусов.

4cepure.JPG

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов: 

asinA=bsinB=csinC

(в решении задачи одновременно пишутся две части, они образуют пропорцию).

Теорема синусов используется для вычисления:

  • неизвестных сторон треугольника, если даны два угла и одна сторона;

  • неизвестных углов треугольника, если даны две стороны и один прилежащий угол.

Так как один из углов треугольника может быть тупым, значение синуса тупого угла находится по формуле приведения

sin180°−α=sinα

.

Наиболее часто используемые тупые углы:

sin120°=sin180°−60°=sin60°=32;sin150°=sin180°−30°=sin30°=12;sin135°=sin180°−45°=sin45°=22.

Радиус описанной окружности

Треуг2.jpg

asinA=bsinB=csinC=2R

, где (R) — радиус описанной окружности.

Выразив радиус, получаем

R=a2sinA

, или

R=b2sinB

, или

R=c2sinC

.

Для вычисления элементов прямоугольного треугольника достаточно (2) данных величин (две стороны или сторона и угол).

Для вычисления элементов произвольного треугольника необходимо хотя бы (3) данных величины.

4cepure.JPG

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Также теорема исполняется для любой стороны треугольника:

Теорема косинусов используется для вычисления:

  • неизвестной стороны треугольника, если даны две стороны и угол между ними;

  • вычисления косинуса неизвестного угла треугольника, если даны все стороны треугольника.

Значение косинуса тупого угла находится по формуле приведения

cos180°−α=−cosα

.

Наиболее часто используемые тупые углы:

cos120°=cos180°−60°=−cos60°=−12;cos150°=cos180°−30°=−cos30°=−32;cos135°=cos180°−45°=−cos45°=−22. 

Если необходимо найти приблизительное значение синуса или косинуса другого угла или вычислить угол по найденному синусу или косинусу, то используется таблица или калькулятор.

Источники:

Рис. 1-3. Треугольник, окружность, © ЯКласс.

Источник

Учебник

Геометрия, 9 класс

Теорема косинусов

Теорема косинусов    

Если в треугольнике даны   две стороны и угол между ними, то такой треугольник один, единственный.   Т.е. любой другой треугольник с такими данными будет в точности равен ему, по   2-му признаку равенства   треугольников.    Ну, раз единственный и неповторимый, то его третья   сторона   должна   быть однозначно   определяема.

_____________________________________________________________________________________

Теорема косинусов    Квадрат стороны треугольника      равен     сумме квадратов двух
   
других сторон минус     удвоенное произведение этих сторон   на    косинус угла между ними.
      
$AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos ACB$

_____________________________________________________________________________________

Факты:

  • Теорема косинусов позволяет найти косинус любого угла по трем известным сторонам, а значит,   и сам угол.
  • Если из трех сторон и одного   угла известны три величины, то четвертое неизвестное можно   всегда вычислить.
  • Теорема косинусов   дает возможность   вычислять   медианы треугольника,   применяя теорему к малым треугольникам.
  • Для прямоугольного треугольника теорема косинусов    «упрощается»   до теоремы Пифагора       $AB^2=AC^2+BC^2$.

       

А если угол тупой? Что означает тригонометрия больших углов?

$cos130=-cos50$,    $sin115=sin65$ ,   $tg135=-tg45$.    

Связь   тригонометрии   тупых   углов    $90 < alpha < 180$    с    тригонометрией    острых     выражается   формулами:      
     $sinalpha=sinleft(180-alpharight)$           $cosalpha=-cosleft(180-alpharight)$        $tgalpha=-tgleft(180-alpharight)$        $ctgalpha=-ctgleft(180-alpharight)$

Если $b^2+c^2-a^2>0$, то $alpha$ — острый;     если $b^2+c^2-a^2=0$, то   $alpha$ — прямой;    если   $b^2+c^2-a^2<0$ , то угол $alpha$ — тупой.

Расчет треугольников по теореме косинусов    

Задача 1:        В треугольнике   $ABC$   сторона   $AC$ равна   $7sqrt{3}$ см,   сторона   $BC$ равна $1$ см ,   угол $C$ = $150^o$ .          Найти   длину стороны   $AB$.

  • Решение:          Применим   теорему косинусов      $AB^2=left(7sqrt{3}right)^2+1-14sqrt{3}cos150$ .
  • Тупой     угол    в $150^o$      выразим     через     острый :       $cos150=cosleft(180-30right)=-cos30=-frac{sqrt{3}}{2}$.         $Rightarrow$      
  • $AB^2=147+1-28sqrt{3}left(-frac{sqrt{3}}{2}right)$      ,         $AB^2= 148 + 21 = 169$           $Rightarrow$                             Ответ:     $AB = 13$

Задача 2:        В треугольнике   $ABC$   сторона   $AC$ равна   $17$ см,   сторона   $BC$ равна $14$ см ,   угол $ACB$ = $60^o$ .
                          Найти   длину третьей стороны   .

  • Решение:          Из   теоремы косинусов для угла    $angle ACB$ :     $Rightarrow$             $AB^2=17^2+14^2-2cdot17cdot14cdotcos60$                 $Rightarrow$   
  • квадрат стороны      $AB^2= 289+196-238 = 247$           $Rightarrow$           Ответ:     $AB = sqrt{247}$

Задача 3:        В   $bigtriangleup ABC$   известны   $AC=3$   , $BC=5$ см,    $AB=6$ .
     Найти   косинус   угла   $C$   и медиану    $BM$   .

  • Решение:          Из   теоремы   косинусов    для стороны    $AB$ выразим косинус требуемого угла $ACB$:   
  • $cos ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}=frac{9+25-36}{30}=-frac{1}{15}$   .      Отрицательное значение косинуса говорит о том, что это тупой   угол $>90^o$
  • Для нахождения    медианы   $ВМ$    распишем     еще раз теорему косинусов, но уже для треугольника     $ВМС$   от угла $С$:
  • $BM^2=BC^2+MC^2-2cdot BCcdot MCcdotcos C$    учтем,   что     медиана   делит сторону   пополам    $MC=frac{AC}{2}=1,5$
  • Подставим     $BM^2=25+2,25-2cdot5cdot1.5cdotleft(-frac{1}{15}right)=27,25+1=28,25$,     получим      $BM=sqrt{28,25}=0,5sqrt{113}$    
  • Ответ:          $cos ACB=-frac{1}{15}$        ,    $BM=0,5sqrt{113}$     .

Задача 4:        В прямоугольном   $bigtriangleup ABC$   известны   $AB=9$ , $BC=3$ см ;    $M$ делит   $AB$ :      $frac{AM}{MB}=frac{1}{2}$.
                          Найти    $CM$   .

  • Решение:         По свойству     аддитивности    отрезка     $AM + MB = 9$ ,   по условию      $frac{AM}{MB}=frac{1}{2}$      $Rightarrow$    $AM = 3$ ,    $MB = 6$
  • Из прямоугольного   $bigtriangleup ABC$    по определению косинуса угла:       $cos B=frac{BC}{AB}=frac{3}{9}=frac{1}{3}$    .
  • Из     $bigtriangleup CMB$       по теореме косинусов найдем   $CM$ :    $CM^2=CB^2+MB^2-2cdot CBcdot MBcdotcos B$       , подставим   числа
  • $CM^2=3^2+6^2-2cdot3cdot6cdotfrac{1}{3}=33$      $Rightarrow$    требуемый   отрезок     $CM=sqrt{33}$      .             Ответ:          $CM=sqrt{33}$

Задача 5:        Одна из сторон треугольника   больше   другой   на   $8$    см, а угол между ними $120^o$ .
                          Найдите периметр треугольника, если длина третьей стороны    $28$ см   .

  • Решение:     Метод введения неизвестного:    Обозначим   одну   из   сторон   треугольника как   $x$ ,
  • выразим нужные величины через х и составим уравнение:    величина   другой стороны будет равна    $x+8$ см.
  • По теореме косинусов:    $28^2=x^2+left(x+8right)^2-2xcdotleft(x+8right)cdotcos120$ ,   где      $cos120=cosleft(180-60right)=-cosleft(60right)=-0,5$,
  • Итак, составили уравнение    $784=x^2+x^2+16x+64-2xleft(x+8right)left(-0,5right)$               $Rightarrow$          $3x^2+24x+720=0$
  • решим   квадратное уравнение : один корень отрицательный — не нужен ,    другой     $x=frac{-24+96}{6}=12$        
  • Периметр    $P=12+left(12+8right)+28=60$.             Ответ:           $60$.

Задача 6:       В     $bigtriangleup ABC$   известны   стороны    $a=15$ , $b=18$,   $c=25$ .          Найти:   углы   $α$,    $β$,    $γ$   (приближённо) .

  • Решение:         Углы    $α$    и    $β$     найдём по теореме косинусов для соответствующих углов.            
  • $cosalpha=frac{b^2+c^2-a^2}{2bc}$ , вычисляем      $cosalpha=frac{18^2+25^2-15^2}{2cdot18cdot25}approx0,8$   ,   привлекаем калькулятор: $alphaapprox36,4^o$    ;
  • $cosbeta=frac{a^2+c^2-b^2}{2ac}$ , вычисляем      $cosbeta=frac{15^2+25^2-18^2}{2cdot15cdot25}approx0,7$   ,   …. калькулятор: $betaapprox45,3^o$       .
  • Найдём   $γ$    по теореме о 180 = сумма углов:    $gamma=180-left(alpha+betaright)$    и    $gammaapprox180-left(36,4+45,3right)approx98,3$   .
  • Ответ:                 $alphaapprox36,4^o$     ,      $betaapprox45,3^o$       ,      $gammaapprox98,3$

          

Задача 7:         В     $bigtriangleup ABC$        $AB=c=3$ м,      $AC = b = 6$ м.   ,    $alpha=60$   .       Найти:   сторону    $a = BC$   ,     углы     $β$,    $γ$    .

  • Решение:           Треугольник   задан    двумя   сторонами   и   углом между ними,    следовательно,   он задан полностью.               
  • По   теореме   косинусов      $a^2=b^2+c^2-2bccdotcosalpha$          найдём сторону     $a$:      
  • $a^2=6^2+3^2-2cdot6cdot3cdotcos60=36+9-36cdotfrac{1}{2}=27$          $Rightarrow$     $a=3sqrt{3}$ .
  • По теореме   косинусов   найдем и    угол    $β$ :     $cosbeta=frac{a^2+c^2-b^2}{2ac}$      ,     $cosbeta=frac{27+9-36}{18sqrt{3}}=0$     $Rightarrow$      $β=90$ .
  • Значит $bigtriangleup ABC$   —    прямоугольный   ,      тогда угол    $γ=90-α$     .          Ответ:    $a=3sqrt{3}$   ,    $β = 90$     ,    $γ=30$   .

Задача 8:         Стороны треугольника равны   $11$   ,    $12$    и     $13$ .    Найти биссектрису, проведенную к стороне, равной 12.

  • дано: $AB=11$   ,     $BC=12$    ,   $AC=13$               Найти биссектрису      $AK=?$ .
  • Решение:     Найдем косинус угла из теоремы косинусов :     $AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos angle ACB$                     
  • Выразим косинус       $cos angle ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}$ ,    $cos angle ACB=frac{13^2+12^2-11^2}{2cdot 13cdot 12}=frac{19}{39}$
  • Найдем отрезки   $BK$ ,   $KC$    на которые биссектриса делит сторону … по теореме биссектрис         $frac{BK}{KC}=frac{AB}{AC}$
  • Система уравнений: $frac{BK}{KC}=frac{11}{13}$ и аддитивность $BK+KC=BC=12$. Получаем    $BK=5,5$ ,    $BK=6,5$
  • Теперь, для нахождения биссектрисы   $AK$   еще раз     используем теорему косинусов для треугольника     $bigtriangleup AKC$
  • $AK^2=AC^2+KC^2-2cdot ACcdot KCcdotcos angle ACB$    подставим значения    $AK^2=13^2+6,5^2-2cdot 13cdot 6,5cdot frac{11}{13}=frac{429}{4}$.
  • Ответ:         $AK=frac{sqrt429}{2}$.

Задача 9:         Стороны треугольника равны   $11$   ,    $12$    и     $13$ .    Найти медиану, проведенную к большей стороне.

  • Решение:         Воспользуемся формулой для длины медианы:        $m_c=frac{1}{2}sqrt{2a^2+2b^2-c^2}$                     
  • Подставим   значения   $m_c=frac{1}{2}sqrt{2cdot11^2+2cdot12^2-13^2}=frac{1}{2}sqrt{242+288-169}=frac{1}{2}sqrt{361}=frac{19}{2}=9,5$     Ответ:       $m_c=9,5$

Задача 10:         В треугольнике     $ABC$     $AB=11$   ,     $AC=23$    ,    медиана      $AK=10$ .           Найти     $BC$ .

  • Решение:          Воспользуемся   формулой   для   длины    медианы      и   подставим    в   неё   данные   из условия:                  
  • $AK=frac{1}{2}sqrt{2cdot11^2+2cdot23^2-BC}$        $Rightarrow$      $100=frac{1}{4}left(242+1058-BC^2right)$         $Rightarrow$   $BC^2=900$          Ответ:           $BC=30$        .    

Упражнения:

Источник

Теорема косинусов отлично помогает в решении треугольников. Решение треугольника – это нахождение всех его сторон и углов. Но если нам даны только стороны треугольника, как определить углы в нем? Вот тогда и приходит на помощь теорема косинусов. Это общий случай теоремы Пифагора, подходящий для треугольника с любым углом, не только с углом 900.

Теорема и доказательство

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Доказательство теоремы косинусов

Докажем теорему. Для этого нарисуем треугольник ABC и докажем, что:

    [BC^2=AB^2+AC^2-2AB cdot AC cdot cos A eqno (1)]

Треугольник АВС к теореме косинусов

Если рассматривать стороны треугольника, как векторы, то будет справедливо равенство:

overrightarrow{BC}=overrightarrow{AC}-overrightarrow{AB}.

В теореме BC в квадрате, значит возведем векторное равенство в квадрат, получим:

    [overrightarrow{BC}^2=overrightarrow{AB}^2+overrightarrow{AC}^2-2overrightarrow{AB}cdot overrightarrow{AC} eqno (2)]

Так как, overrightarrow{BC}^2={BC}^2, overrightarrow{AC}={AC}^2, а скалярное произведение векторов равно произведению их модулей на косинус угла между ними, то есть overrightarrow{AB}cdot overrightarrow{AC}={AB}cdot {AC} cdot cos A.

Подставим все в формулу (2):

BC^2=AB^2+AC^2-2AB cdot AC cdot cos A.

Что и требовалось доказать.

Следствие теоремы косинусов

Проведем высоты CD:

Треугольник АВС к следствию теоремы косинусов

Обратим внимание, что AC cdot cos A = AD. То есть AD – это проекция стороны AC на сторону AB треугольника ABC. Если угол А острый, то AC cdot cos A >0, если угол А тупой, то косинус угла А будет отрицательным и AC cdot cos A <0. То есть из теоремы косинусов вытекает важное следствие:

квадрат стороны треугольника равен сумме квадратов двух других сторон “pm” удвоенное произведение одной из них на проекцию другой на эту сторону. Знак + надо брать, если угол тупой, а знак -, если угол острый.

Задачи на теорему косинусов

Задача 1

Найдите BC, если дано: angle B = 60^{circ},  AB=8, AC=4sqrt 7.

Задача на теорему косинусов

Решение: Так как нам известен угол между сторонами AB и BC и известна сторона AC – мы сможем найти сторону ВС,  если воспользуемся теоремой косинусов.

Из теоремы косинусов AC^2={AB}^2+{BC}^2-2AB cdot {BC} cos {angle B} выразим сторону BC.

Получим:

{BC}^2-2AB cdot {BC} cos {angle B}-AC^2+{AB}^2 = 0

Обозначим {BC}=x

Тогда

x^2-2AB cdot cos {angle B} cdot x-AC^2+{AB}^2=0

Получаем квадратное уравнение. Подставим в него значения и решим:

x^2-2 cdot 8 cdot frac{1}{2} x-{(4 sqrt 7)}^2+8^2=0

x^2-8x-112+64=0

x^2-8x-48=0

Находим дискриминант:

D=b^2-4ac=64-4cdot(-48)=64+192=256.

Тогда x_1=frac{8+16}{2}=frac{24}{2}=12.

x_2=frac{8-16}{2}=frac{-8}{2}=-4 – не может быть длиной стороны треугольника.

Ответ: 12.

Задача 2

В треугольника ABC AC=BC, angle C=120^{circ}, AB=6sqrt{3}. Найдите AC

Решение: Нарисуем треугольник ABC. Это равнобедренный треугольник.

Треугольник к задаче на теорему косинусов 2

Запишем теорему косинусов для сторону AB так как нам дан угол между двумя другими сторонами:

    [AB^2={AC}^2+{BC}^2-2AC cdot {BC} cos {angle 120^{circ}} eqno (1)]

.

Так как AC=BC, то из формулы (1), получим:

AB^2=2{AC}^2-2{AC}^2 cdot cos {angle 120^{circ}}

Сделаем замену: AC=x:

AB^2=2{x}^2-2{x}^2 cdot cos {angle 120^{circ}},

перенесем {AB}^2 в правую часть равенства и получим квадратное уравнение:

2{x}^2-2{x}^2 cdot cos {angle 120^{circ}}-{AB}^2=0,

Подставим значения:

2{x}^2-2{x}^2 cdot cos {angle 120^{circ}}-{(6sqrt{3})}^2=0

cos {angle 120^{circ}}=-frac{1}{2}

2{x}^2+{x}^2-108=0

3{x}^2=108

{x}^2=36

x=sqrt{36}

x=6

Так как x=AC, значит, AC=6.

Ответ: 6

Задача 3

Решите треугольник ABC, если известно, что angle A=30^{circ}, AB=4, angle C=45^{circ}.

К задаче 3 по теореме косинусов

Решение: Решить треугольник – это значит, найти все его стороны и все углы. Нам два угла даны, значит, зная, что сумма всех углов в треугольнике равна 180^{circ} получим:

angle B = 180^{circ}-30^{circ}-45^{circ}=105^{circ}.

Обозначим неизвестные стороны треугольника: AC=x,   BC=y.

Выразим сторону треугольник AB по теореме косинусов:

    [AB^2={x}^2+y^2-2{xy} cdot cos {45^{circ}}eqno (1)]

Выразим сторону треугольника BC=y по теореме косинусов:

y^2={x}^2+{AB}^2-2{x}cdot{AB} cdot cos {30^{circ}}

или

    [y^2={x}^2+16-8{x}cdot cos {30^{circ}} eqno (2)]

Решим уравнения (1) и (2) совместно, записав их в систему уравнений:

    [left{ begin{aligned} AB^2={x}^2+y^2-2{xy} cdot cos {45^{circ}}\ y^2={x}^2+16-8{x}cdot cos {30^{circ}}.\ end{aligned} right.]

    [left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ y^2={x}^2+16-4{x}cdot sqrt{3}.\ end{aligned} right.]

Преобразуем второе уравнение системы:

    [left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ -16={x}^2-y^2-4{x}cdot sqrt{3}.\ end{aligned} right.]

Сложим первое и второе уравнения системы и запишем получившееся уравнение вместо второго уравнения, получим:

    [left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ 0=2{x}^2-xy sqrt{2}-4{x}cdot sqrt{3}.\ end{aligned} right.]

Из второго уравнения выразим y:

xy sqrt{2}=2x^2-4x sqrt{3}

y=frac{2x^2-4x sqrt{3}}{x sqrt{2}}

y=frac{2x-4sqrt{3}}{sqrt{2}}

Итак, мы выразили y из второго уравнения системы, теперь возьмем и подставим его в первое уравнение и сделаем необходимые преобразования.

16=x^2+(frac{2x-4sqrt{3}}{sqrt{2}})^2-x sqrt{2}(frac{2x-4sqrt{3}}{sqrt{2}}), раскрываем скобки и умножим левую и правую части уравнения на 2:

32=2x^2+4x^2-16x sqrt{3}+16 cdot 3-2x(2x-4 sqrt{3})

2x^2-8x sqrt{3}+48-32=0

2x^2-8x sqrt{3}+16=0

Разделим левую и правую части уравнения на 2:

x^2-4x sqrt{3}+8=0.

Получили квадратное уравнение. Решим его.

Находим дискриминант:

D=b^2-4ac=(4 sqrt{3})^2-4 cdot 8 cdot 1=16 cdot 3 - 32=48-32=16

Тогда корни уравнения:

x_1=frac{-b-sqrt{D}}{2a}=frac{4 sqrt{3}-4}{2}=2 sqrt{3}-2

x_2=frac{-b+sqrt{D}}{2a}=frac{4 sqrt{3}+4}{2}=2 sqrt{3}+2.

Оба значения подходят – они положительны. Находим, y:

y_1= frac{2(2 sqrt{3}-2)-4 sqrt{3}}{sqrt{2}}=frac{-4}{sqrt{2}} – отрицательное значение нам не подходит.

y_2= frac{2(2 sqrt{3}+2)-4 sqrt{3}}{sqrt{2}}=frac{4}{sqrt{2}}=2 sqrt{2}.

Таким образом, получаем следующие значения x=2 sqrt{3}+2, y=2 sqrt{2}.

Вы можете самостоятельно сделать проверку и убедиться в том, что данные значения верны.

Ответ: AC=2 sqrt{3}+2,  BC=2 sqrt{2}.

Теорема косинусов для треугольника очень помогает в решении геометрических задач, однако некоторые задачи усложняются, если не знать еще одну теорему – синусов. Например, третью задачу мы могли решить гораздо проще – используя теорему синусов, с помощью которой мы бы довольно быстро получили тот же результат для y. Однако, с ней мы бы получили лишь приближенное значение x. Теорема косинусов дает нам точный результат. Однако, в дальнейшем, когда вы выучите две теоремы – рекомендуем решать задачи, используя их обе.

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти свой район москвы
  • Как составить уравнение прямой проходящей через точку параллельно оси абсцисс
  • Майнкрафт как найти дельфина
  • Как найти равновесную цену калькулятор
  • Недоступен в вашей стране play market как исправить

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии