-
Функции
Система
MathCAD содержит большой набор встроенных
элементарных функций. Функции задаются
своими именами и значениями аргумента,
заключёнными в круглых скобках. Функции,
как и переменные, и числа, могут входить
в состав математических выражений. В
ответ на обращение к ним, функции
возвращают вычисленные значения. Ниже
представлены некоторые из этих функций.
-
Тригонометрические
функции
sin (z) — синус cos
(z) — косинус
tan (z) — тангенс sec
(z) — секанс
csc (z) — косеканс cot
(z) — котангенс
-
Гиперболические
функции
sinh (z) — гиперболический
синус
cosh(z) — гиперболический
косинус
tanh(z) — гиперболический
тангенс
sech(z) — гиперболический
секанс
csch(z) — гиперболический
косеканс
coth(z) — гиперболический
котангенс
-
Обратные
тригонометрические функции
asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс
1.2.4 Обратные гиперболические функции
asinh
(z) — обратный гиперболический синус
acosh(z)
— обратный гиперболический косинус
atanh(z)
— обратный гиперболический тангенс
-
Показательные
и логарифмические функции
exp (z) — экспоненциальная
функция
ln (z) — натуральный
логарифм
log (z) — десятичный
логарифм
1.2.6 Функции с
условиями сравнения
ceil (x) — наименьшее
целое, большее или равное х
floor(x) – наибольшее
целое, меньшее или равное х
mod(x,y) – остаток
отделения х/у
со знаком х
angle(x,y) – положительный
угол с осью х
для точки с координатами (х,у).
Пример: 1.1.
Требуется
вычислить значение y=sin(x)
при x=π/6.
Ставим курсор в левой части экрана и
набираем
x:=π/6 y:=sin(x)
x=0.5
Греческие
буквы следует набирать с помощью
специальной панели инструментов, которая
появляется на экране при нажатии на
пиктограмму
-
Функция if
Функция
if
предназначена для создания условных
выражений:
if
(условие,
выражение _1, выражение _2)
Если
в этой функции условие выполняется, то
будет вычисляться выражение _1, в противном
случае – выражение _2.
Условие
– это оператор для сравнения двух
величин, которые называются оператором
отношения или логическим оператором.
Ниже приводится перечень логических
операторов и правила набора их на
клавиатуре:
Таблица
1.1
|
Оператор |
Клавиши |
Наименование |
|
x>y |
x>y |
х больше у |
|
x<y |
x<y |
х меньше у |
|
x >y |
x ctrl0 y |
х больше или |
|
x <y |
x ctrl9 y |
х меньше или |
|
x # y |
x ctrl3 y |
х неравно у |
|
x = y |
x ctrl=y |
х равно у |
Не
следует путать оператор сравнения (знак
равенства) с похожим знаком вывода
значений переменных. В системе MathCAD знак
равенства как оператор отношения имеет
больший размер и более жирное написание.
Выражения
с логическими операторами возвращают
логическое значение, соответствующее
выполнению или невыполнению условия,
заданного оператором. Если условие
выполнено, возвращается единица, если
не выполнено – нуль (0).
Пример
1.2: Требуется
рассчитать мгновенное значение тока,
полученного в результате однополупериодного
выпрямления синусоидального тока i
= 50 sin(314 t) в
различные моменты времени.
i := if(i>0, 50*sin(314*t),
0)
i = 25.
Чтобы
вычислить значение выпрямленного тока
в другие моменты времени, достаточно в
самом первом выражении изменить значение
t и
задать режим вычислений.
-
Функции пользователя
Несмотря
на широкий набор встроенных функций,
часто возникает необходимость расширить
систему новыми функциями, представляющими
интерес для пользователя. Функции
пользователя вводятся с применением
следующего выражения:
<Имя_функции>
(<Список_параметров>) := <Выражение>,
где <Имя_функции>
– любой идентификатор;
<Список_параметров>
– перечень
используемых в выражении переменных,
разделённых запятыми;
<Выражение>
– любое математическое выражение,
содержащее доступные системе операторы
и функции с операндами и аргументами,
указанными в списке параметров.
Пример 1.3.
Использование функции двух переменных:
a:=1 b:=2 m:=md(a,b)
m=2.236
Соседние файлы в папке ТОЭ 4 семестр
- #
- #
- #
- #
- #
- #
- #
- #
Все углы в
тригонометрических функциях измеряются в радианах.
• acosh(X) – возвращает гиперболический арккосинус для каждого элемен
та X. Пример:
>>Y = acosh (0.7)
Y=
0 + 0.7954i
Рис. 3.3. Графики синусоиды, прямоугольных,
пилообразных и треугольных колебаний
• acoth(X) – возвращает гиперболический арккотангенс для каждого эле
мента X. Пример:
>>Y = acoth (0.1)
Y = 0.1003 + 1.5708i
• acsch(X) – возвращает гиперболический арккосеканс для каждого эле
мента X. Пример:
>> Y = acsch(1)
Y=
0.8814
• asech(X) – возвращает гиперболический арксеканс для каждого элемента
X. Пример:
>> Y = asech(4)
Y=
0 + 1.3181i
• asinh(X) – возвращает гиперболический арксинус для каждого элемента
X. Пример:
>> Y = asinh (2.456)
Y=
1.6308
• atanh(X) – возвращает гиперболический арктангенс для каждого элемен
та X. Пример:
>> X=[0.84 0.16 1.39];
>> atanh (X)
ans = 1.2212
0.1614
0.9065 + 1.5708i
Рис. 3.4. Графики периодических сигналов без разрывов
• cosh(X) – возвращает гиперболический косинус для каждого элемента X.
178
Пример:
Программные средства математических вычислений
Встроенные элементарные функции
179
>> X=[1 2 3];
>> cosh(X)
ans = 1.5431 3.7622
10.0677
• coth(X) – возвращает гиперболический котангенс для каждого элемента
X. Пример:
>> Y = coth(3.987)
Y=
1.0007
• csch(x) – возвращает гиперболический косеканс для каждого элемента X.
Пример:
>> X=[2 4.678 5;0.987 1 3];
>> Y = csch(X)
Y=
0.2757
0.0186
0.0135
0.8656
0.8509
0.0998
• sech(X) – возвращает гиперболический секанс для каждого элемента X.
Пример:
>> X=[pi/2 pi/4 pi/6 pi];
>> sech(X)
ans = 0.3985 0.7549 0.8770
Рис. 3.5. Графики гиперболических функций
0.0863
• sinh(X) – возвращает гиперболический синус для каждого элемента X.
Пример:
>> X=[pi/8 pi/7 pi/5 pi/10];
>> sinh(X)
ans = 0.4029 0.4640 0.6705
0.3194
• tanh(X) – возвращает гиперболический тангенс для каждого элемента X.
Пример:
>> X=[pi/2 pi/4 pi/6 pi/10];
>> tanh(X)
ans = 0.9172 0.6558 0.4805
0.3042
Следующий m файл сценарий (программа) строит графики (рис.
Самоучитель MathCAD
И другие программы этой серии
Самоучитель MathCAD
Все углы в
тригонометрических функциях измеряются в радианах.
• acosh(X) – возвращает гиперболический арккосинус для каждого элемен
та X. Пример:
>>Y = acosh (0.7)
Y=
0 + 0.7954i
Рис. 3.3. Графики синусоиды, прямоугольных,
пилообразных и треугольных колебаний
• acoth(X) – возвращает гиперболический арккотангенс для каждого эле
мента X. Пример:
>>Y = acoth (0.1)
Y = 0.1003 + 1.5708i
• acsch(X) – возвращает гиперболический арккосеканс для каждого эле
мента X. Пример:
>> Y = acsch(1)
Y=
0.8814
• asech(X) – возвращает гиперболический арксеканс для каждого элемента
X. Пример:
>> Y = asech(4)
Y=
0 + 1.3181i
• asinh(X) – возвращает гиперболический арксинус для каждого элемента
X. Пример:
>> Y = asinh (2.456)
Y=
1. 6308
• atanh(X) – возвращает гиперболический арктангенс для каждого элемен
та X. Пример:
>> X=[0.84 0.16 1.39];
>> atanh (X)
ans = 1.2212
0.1614
0.9065 + 1.5708i
Рис. 3.4. Графики периодических сигналов без разрывов
• cosh(X) – возвращает гиперболический косинус для каждого элемента X.
178
Пример:
Программные средства математических вычислений
Встроенные элементарные функции
179
>> X=[1 2 3];
>> cosh(X)
ans = 1.5431 3.7622
10.0677
• coth(X) – возвращает гиперболический котангенс для каждого элемента
X. Пример:
>> Y = coth(3.987)
Y=
1.0007
• csch(x) – возвращает гиперболический косеканс для каждого элемента X.
Пример:
>> X=[2 4.678 5;0.987 1 3];
>> Y = csch(X)
Y=
0.2757
0.0186
0.0135
0.8656
0.8509
0.0998
• sech(X) – возвращает гиперболический секанс для каждого элемента X.
Пример:
>> X=[pi/2 pi/4 pi/6 pi];
>> sech(X)
ans = 0.
Рис. 3.5. Графики гиперболических функций
0.0863
• sinh(X) – возвращает гиперболический синус для каждого элемента X.
Пример:
>> X=[pi/8 pi/7 pi/5 pi/10];
>> sinh(X)
ans = 0.4029 0.4640 0.6705
0.3194
• tanh(X) – возвращает гиперболический тангенс для каждого элемента X.
Пример:
>> X=[pi/2 pi/4 pi/6 pi/10];
>> tanh(X)
ans = 0.9172 0.6558 0.4805
0.3042
Следующий m файл сценарий (программа) строит графики (рис.
<< Назад 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
Вперед >>
Алгебра К12: тригонометрия с примерами на Mathcad 15 | Mathcad Prime
|
переменные и Числовые функции — это соответствие между элементами двух множеств, при котором каждому элементу одного множества (переменной, или аргументу) ставится в соответствие не более одного элемента другого множества (значение функции) |
|
периодические Периодическая функция — для которой выполнено условие f(x)=f(x+Т)=f(x-Т).  Число Т Число Тназывают периодом функции. |
|
радианы и Измерение угла: если окружность покрыть равномерной сеткой от 0 до 2π (или от 0 до 360°), то любой угол можно измерить в радианах (долях 2π) или градусах. Радианная мера угла α = (π/180)⋅(α в °). Очевидно: α = α ± 2π = α ± 360° |
|
сумма углов Сумма углов любого треугольника α1+α2+α3 равна π = 180°, сумма углов многоугольника (N-угольника) равна π⋅(N-2) = 180°⋅(N-2).  |
|
прямоугольный Это треугольник, один из углов которого равен 90° = π/2. Стороны x, y при прямом угле называются катетами, а третья сторона — это гипотенуза |
|
теорема Прямоугольный треугольник задает простое соотношение между его сторонами: сумма квадратов длин катетов x, y равна квадрату длины гипотенузы: x² + y² = z² |
|
sin и cos, tg Для острого угла α прямоугольного треугольника можно определить синус, как отношение противолежащего к углу катета y к гипотенузе z: sin(α) = y/z, косинус — как отношение прилежащего катета x к гипотенузе: cos(α) = x/z, тангенс и котангенс — как отношение катетов: tg(α) = y/x = sin(α)/cos(α) ctg(α) = x/y = 1/tg(α) |
|
теорема Для любого треугольника со сторонами х1, х2 и х3 и противолежащими им углами α1, α2 и α3 справедливо: x1/sin(α1) = x2/sin(α2) = x3/sin(α3) = 2R, где R — это радиус окружности, описанной вокруг треугольника |
|
теорема Для любого треугольника со сторонами a,b,c и углом α между сторонами b,c справедливо: a² = b² + c² — 2⋅b⋅c⋅cos(α).  Следствие: теорему Пифагора, при α=90°. |
|
единичная Это окружность радиусом R=1. По точкам (x,y) на ней удобно отсчитывать углы и определять тригонометрические функции (в том числе, для α < 0 и α > π/2). В частности, синус sin(α) = y, косинус cos(α) = x, тангенс tg(α) = y/x, котангенс ctg(α) = x/y, секанс sec(α) = 1/cos(α) = 1/x, косеканс csc(α) = 1/sin(α) = 1/y. |
|
тригонометрические Некоторые свойства тригонометрических функций: все они периодические sin(x)=sin(x+2π), четные cos(-x)=cos(x) или нечетные sin(-x)=-sin(x), tg(-x)=-tg(x) |
|
тригонометрические Основное тригонометрическое тождество: sin²(x)+cos²(x)=1, формулы приведения sin(k⋅π/2-x)=cos(x), tg(π/2+x)=-ctg(x) и т.  п., формулы сложения, двойного угла, половинного угла, преобразование суммы тригонометрических функций в произведение и т.д. |
|
arcsin, Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. Арксинус — это угол, синус которого равен х, т.е. если sin(α) = х, то арксинус arcsin(х) = α. Аналогично, арккосинус arccos(х) = α, если cos(α) = x и арктангенс arctg(х) = α, если tg(α) = x.  Причем arcsin определяет Причем arcsin определяет-π/2 ≤ α ≤ π/2, а arccos для 0 ≤ α ≤ π. Очевидно: arcsin(-х) = -arcsin(х), arccos(-х) = π — arccos(х). |
|
гармонические Гармонический закон колебаний — это y(t) = A⋅cos(ω⋅t+φ) или y(t) = A⋅sin(ω⋅t+φ) = A⋅cos(ω⋅t+φ-π/2). Параметры A, ω, φ — это амплитуда, круговая частота и начальная фаза колебаний. Период колебаний равен Т = 2π/ω. |
|
Анна Малкова: Курс по тригонометрии от А.  Малковой: четные и Малковой: четные инечетные функции, периодичность, градусы и радианы, тригонометрические тождества, синус, косинус, тангенс, уравнения и неравенства |
numpy.arcsin — Руководство NumPy v1.24
- numpy.arcsin ( x , /, out = none , * , где = true , Casting = ‘Some_kind’ , Order = ‘K’ , DTYP subok=True [ подпись , extobj ]) =
-
Инверсный синус, поэлементный.
- Параметры:
-
- х array_like
-
y -координата на единичной окружности.
- out ndarray, None или кортеж из ndarray и None, необязательный
-
Местоположение, в котором сохраняется результат. Если он предусмотрен, он должен иметь
форма, на которую транслируются входные данные.Если не указано или Нет,
возвращается только что выделенный массив. Кортеж (возможен только как
аргумент ключевого слова) должен иметь длину, равную количеству выходов. - , где array_like, необязательный
-
Это условие передается по входу. В местах, где
условие равно True, массив из будет установлен в результат ufunc.
В другом месте массив из сохранит исходное значение.
Обратите внимание, что если неинициализированный массив из создан по умолчанию
out=None, места внутри него, где условие False, будут
остаются неинициализированными. - **kwargs
-
Другие аргументы, содержащие только ключевые слова, см.
документы ufunc.
- Возвращает:
-
- угол ndarray
-
Арксинус каждого элемента в x , в радианах и в
закрытый интервал[-pi/2, pi/2].
Это скаляр, если x является скаляром.
См. также
-
sin,cos,arccos,tan,arctan,arc.0068
Примечания
arcsin— многозначная функция: для каждых x существует бесконечное число
много чисел z таких, что (sin(z) = x). Конвенция заключается в
вернуть угол z , действительная часть которого лежит в [-pi/2, pi/2].Для типов входных данных с действительным знаком arcsin всегда возвращает действительный вывод.
Для каждого значения, которое не может быть выражено как действительное число или бесконечность,
это даетнанови устанавливает 9{-1}.Каталожные номера
Абрамовиц, М. и Стегун, И. А., Справочник по математическим функциям ,
10-е издание, Нью-Йорк: Довер, 1964, стр. 79 и далее.
https://personal.math.ubc.ca/~cbm/aands/page_79.htmПримеры
>>> np.
arcsin(1) # пи/2 1.5707963267948966 >>> np.arcsin(-1) # -pi/2 -1,5707963267948966 >>> np.arcsin(0) 0,0
arcsin matlab-掘金
紫极神光Q1564658423
1 номер
МАТЛАБ
【识别】 基于 基于 Matlab 指纹 识别 【含 Matlab 源码 029 期】
指纹 识别 主要 分 三 步骤 : 指纹 预 处理 、 特征 提取 、 指纹 与。 还是 还是 、 、 、 都 都 匹配 匹配 匹配 匹配 匹配提取 指纹 有效 特征, 而 提取 的 性能 很 大 程度 上 要 依赖 于 图像 的 质量 质量 在 实际 应用 中 由于 采集 条件 采集 设备 的 因素 采集 到 指纹 指纹 图像 比较 差 很多 问题 因素 采集 到 指纹 图像 差 容易 很多 问题,影响后续处理的效果。...
- 271
-
1
烧灯续昼2002
3月前
数学
【高等数学基础进阶】不定积分-练习 & 定积分与反常积分-补充
9{2} x) = frac {x} { sin x} $, 求 $ int frac { sqrt {x}} { sqrt {1-x
- 11
-
点赞
沧叔解码
4月前
Люсен
搜索引擎
数据结构
Lucene 源码 系列 (十) : FST 构建
背景 都 知道 检索 检索 引擎 的 核心 倒排 倒排 倒排 就 是 所在 文档 列表 (当然 可以 包含 在 对应 中 的 信息 信息) , 怎么 怎么 怎么 怎么 , ,就是term映射倒排位置的
- 605
7
4
tcfellow
4年前
求有向图G的转置图GT
有向图G=(V,E)的转置是图輌GT=(V,ET) ∈E 当且 仅 当 ∈E , 即 gt 就 是 g 的 边 反向 所 组成 的 图。 请 按照 相邻 和 邻接表 两 表示 法 写出 从 g 计算 的 有效 算法 算法 , , , 种 法 写出 从 gt 的 有效 算法 算法 算法 算法 邻接表 两 种并 确定 的 时间 代价。 可以 看出 循环 了 所有 的 边 , 算法 为 为 o (e) , , 为 边 的 数目。
- 1136
-
点赞
tk103331
3 этажа
运维
C/C ++ 单测 覆盖率 分析
前 时间 , 负责 的 Ci 平台 有 需求 想 做 C/C ++ 单测 统计 , 之前 做 过 过 过 相关 工作 , 没有 过 C/C ++ 的 测试 测试 , ,经过 一 折腾 , 搞 了 一 个 基本 可 用 方案 方案 把 分析 过程 记录 下来 , 分享 给。 再 执行 执行 进行。 打印 信息 测试 用例 及 其 情况 情况 , 测试 统计 等。 包括 测试 及 运行 情况 , 结果 等。。 包括 测试 及0031
- 3325
-
2
辰酱czklove
1年前
前端
Canvas- 事件 交互
Canvas 事件 交互 交互 本质 是 一 张 位图 位图 , 所有 这 图片 是 支持 的 各 事件 的 位图 位图 所有 这 画布 是 支持 鼠标 各 事件 的 的 , 对于 其 画布 上 的 内容 不 支持 事件 和 但 但 但 但 和 和 和 和 和
- 426
-
3
有出路
1年前
后端
数据结构
考研 结构 第 第 6 章图 | 图 的 应用 二 最 短 路径 三 、 拓扑 排序 排序 排序 排序 带 带 权图 , 从 一 个 顶点 顶 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 点 𝑣𝑖 (可能不止一 条)上所经过边上的权值之和定义为该路径带权路径长度,把带权路径长 度最短的那条路径称为最短路径 求解最短路
- 490
-
26
大石头的笔记
2年前
питон
Python 实现 dijkstra 算法-最 短 路径 问题
本 文 借鉴于 张广河 教授 主编 的 数据 结构》 , 其中 代码 进行 了 完善。 某 某 源点 各 短 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径 路径
- 137
-
点赞
头发保卫者
1年前
算法
后端
满足 不等式 的 的 的 问题 的 近似 算 法 法
1.
- 1750
-
4
紫极神光Q1564658423
1年前
人工智能
. 200
1
影子就是我41673
4年前
Весна
HTTP
Ява
httpfetch-一款java语言编写优雅的http接口调用组件
当 提到 提到 java 调用 http 请求 时 , 想到 的 是 是 我们 是 不 是 一 种 更 优雅 的 方式 呢 , , 通过 通过 , , , , , , , , , , , , , , , , , , , , , , , , , , ,
8
18
紫极神光Q1564658423
1年前
МАТЛАБ
【疲劳检测】基于matlab GUI疲劳检测【含Matlab源码 126期】
% GUI Код MATLAB для GUI.
- 122
-
1
佛怒火莲Q1564658423
1年前
МАТЛАБ
. РУКИ Код MATLAB для han
- 148
-
1
紫极神光Q1564658423
1 номер
МАТЛАБ
.
1
紫极神光Q1564658423
1年前
人工智能
【分析】 基于 基于 matlab gui 鼠笼式 异步 转子 断条 故障 诊断 【含 含 matlab 源码 1089 期】
一 简介 基于 基于 鼠笼式 异步 电机 断条 断条 故障 二 、 、 运行 运行 鼠笼式 异步 转子 断条 诊断 二 、 、结果 四、备注 版本:2014a
- 114
-
2
紫极神光Q1564658423
1年前
МАТЛАБ
【肌电信号】基于matlab GUI MUAP波形【含Matlab源码 736期】
% MUAPGUI M-файл для MUAPgui.
- 108
-
2
紫极神光Q1564658423
1年前
МАТЛАБ
. ('CALLBACK',hObject,eventData,handles,...% ...
- 75
-
3
紫极神光Q1564658423
1年前
МАТЛАБ
【分析】 基于 基于 Matlab Gui 学生 成绩 查询 【含 含 Matlab 源码 604 期】
基于 Matlab Gui 学生 查询 系统 : 可 查询 学生 各 学科 成绩 平均 分及 排名。% Ченгичаксун m-file for chengjhan. % singleton*.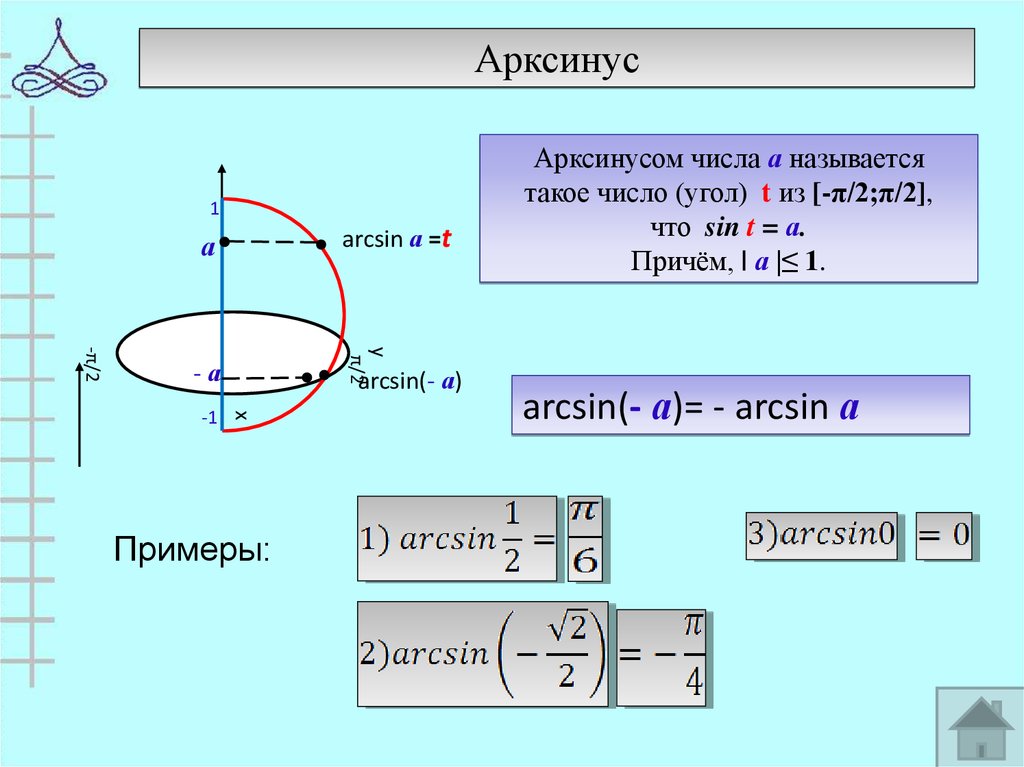
- 74
-
1
佛怒火莲Q1564658423
1年前
МАТЛАБ
【分析】 基于 基于 Matlab Gui 学生 成绩 查询 【含 含 Matlab 源码 604 期】
一 简介 基于 基于 学生 成绩 查询 系统 : : 查询 学生 各 学科 、 排名。 、 : : : 查询 学生 学科 、 排名。 、 : : : : : 源代码 、 varargout = chengjichaxun (varargin) % CH
- 72
-
1
紫极神光Q1564658423
1年前
МАТЛАБ
【去 噪】 基于 基于 基于 基于 图像 图像 均值 均值+中值+高斯 低通+多 种 小波 变换 图像 去 噪 【含 Matlab 源码 856 期】
% Изображение Процесс код Matlab для ImageProcess.
1.5. Некоторые стандартные функции MathCAD
Рассмотрим некоторые стандартные функции системы MathCAD. Введем специальные обозначения для аргументов функций. Пусть первый символ имени аргумента обозначает его тип:
M – квадратная матрица;
V – вектор (матрица из одного столбца);
A – произвольная матрица;
S – симметричная матрица;
G – произвольная матрица или число;
X – вектор или число;
Z – комплексная матрица или число;
z – комплексное число;
прочие символы – скалярные величины.
Экспоненциальные и логарифмические функции
exp(X) – экспонента от X;
ln(X) – натуральный логарифм от X;
log(X) – десятичный логарифм от X;
log(X,b) – логарифм от X по основанию b.
Гиперболические и тригонометрические (прямые и обратные) функции
sin(X), cos(X), tan(X), cot(X), sec(X), csc(X) – соответственно синус, косинус, тангенс, котангенс, секанс, косеканс от X, причем аргументы указываются в радианах;
sinh(X), cosh(X), tanh(X), coth(X), sech(X), csch(X) – аналогичные гиперболические функции;
asin(z), acos(z), atan(z), acot(z), asec(z), acsc(z) – соответственно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс от z.
Функции для работы с комплексными числами
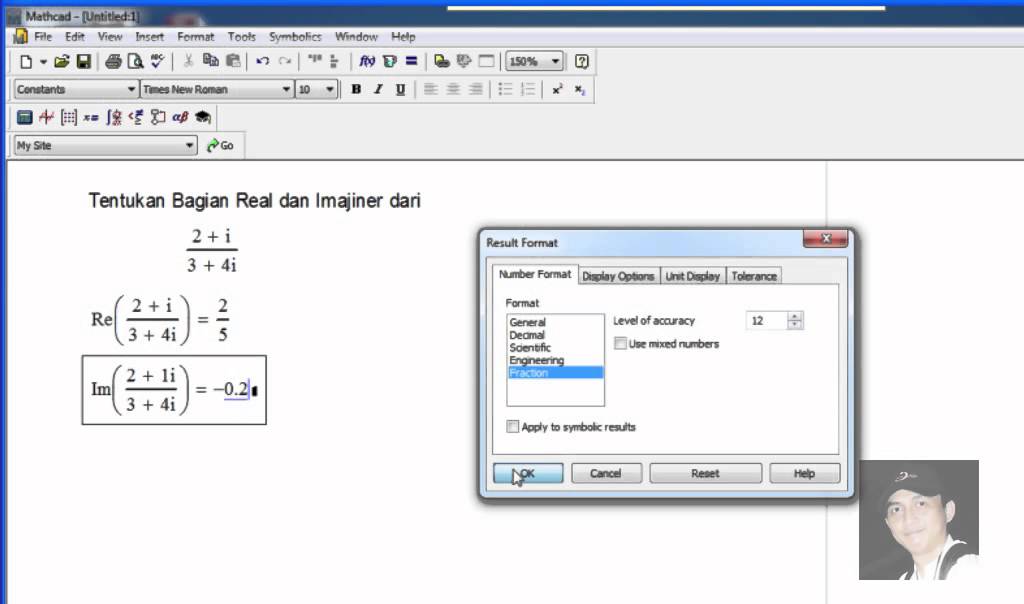
Re(Z), Im(Z) – соответственно вещественная и мнимая части комплексного числа Z;
arg(z) – аргумент комплексного числа z (в радианах).
Матричные функции
length(V) – возвращает число элементов вектора V;
cols(A) – возвращает число столбцов матрицы A;
rows(A) – возвращает число строк матрицы A;
matrix(m, n, f) – матрица размером mxn, значения элементов матрицы определяются f – функцией f (i, j) от двух переменных (номера строки и номера столбца). Эта функция должна быть предварительно определена пользователем;
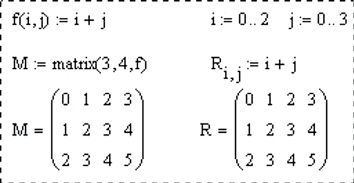
identity(n) – единичная матрица n×n;
tr(M) – след матрицы M (сумма элементов главной диагонали);
rank(A) – ранг матрицы M;
norme(M) – эвклидова норма матрицы M, то есть корень квадратный из суммы квадратов всех элементов;
eigenvals(M) – вектор, элементы которого являются собственными числами матрицы M;
eigenvecs(M) – матрица, состоящая из нормализованных собственных векторов матрицы M;
cholesky(S) – возвращает нижнетреугольную матрицу L – результат разложения Холецкого вида L∙LT = S;
lu(M) – возвращает матрицу размера n×3n, состоящую из трех соединенных матриц P, L, U, являющихся результатом LU-разложения вида P∙M = L∙U.
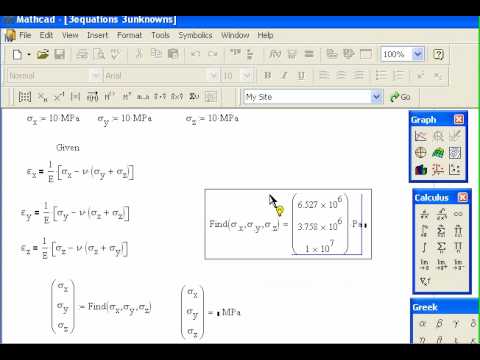
Пример вычислений с матричными функциями: нахождение собственного числа путем решения матричного уравнения det(M – λE) = 0 и с помощью функции eigenvals.

Элементы статистического анализа данных
gmean(G1,G2,G3…) – среднее геометрическое аргументов;
mean(G1,G2,G3…) – среднее арифметическое аргументов;
var(G1,G2,G3…) – дисперсия;
stdev(G1,G2,G3…) – среднеквадратичное отклонение.
Дискретные преобразования
fft(V1), ifft(V2) – прямое и обратное быстрые преобразования Фурье над вещественными данными. V1 – вектор из 2m элементов, V2 – вектор из 1 + 2m–1 элементов, m > 2;
cfft(A), icfft(A) – прямое и обратное преобразования Фурье над вещественными и комплексными векторами и матрицами;
wave(V), iwave(V) – прямое и обратное вейвлет-преобразования, V – вектор из 2m элементов, m – целое число.
Аппроксимация, интерполяция и экстраполяция
Аппроксимация – поиск функции, которая с заданной степенью точности описывает исходные данные.
Интерполяция – определение наиболее правдоподобных промежуточных значений в интервале между известными значениями (подбор гладкой кривой, проходящей через заданные точки или максимально близко к ним).
Экстраполяция – определение наиболее правдоподобных последующих значений на основании анализа предыдущих значений (предсказание дальнейшего поведения неизвестной функции).
Применяются следующие функции MathCAD:
regress(VX,VY,k) – возвращает вектор данных, используемый для поиска интерполирующего полинома (a0 + a1x + a2x2 + … + akxk) порядка k. Полином должен описывать данные, состоящие из упорядоченных значений аргумента (VX) и соответствующих значений неизвестной функции (VY), то есть график полинома должен проходить через все точки, заданные координатами (VX, VY), или максимально близко к этим точкам;
interp(VS,VX,VY,x) – возвращает интерполированное значение неизвестной функции при значении аргумента x. VS – вектор значений, который вернула функция regress. VX,VY – те же данные, что и для regress. Функции interp и regress используются в паре;
predict(V,m,n) – возвращает вектор из n предсказанных значений на основании анализа m предыдущих значений из вектора V. Предполагается, что значения функции в векторе V были получены при значениях аргумента, взятых последовательно, с одинаковым шагом. Используется алгоритм линейной предикции. Наиболее целесообразно использовать predict для предсказания значений по данным, в которых отмечены колебания.
Для интерполяции система MathCAD использует подход, основанный на применении метода наименьших квадратов.
Примеры интерполяции и экстраполяции:
1.5.1. Пусть заданы координаты пяти точек (1; 1), (2; 2), (3; 3), (4; 2), (5; 3), представляющих результаты измерения значений некоторой неизвестной функции при различных значениях x. Необходимо подобрать интерполирующую функцию (гладкую кривую), проходящую через заданные точки.
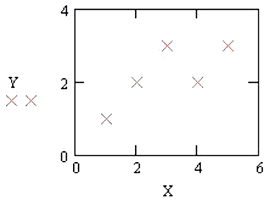
1.5.2. Дана функция y(i) = e–i/10∙sin (i). Известны значения данной функции при i = 0, 1, …, 10. Основываясь на десяти последних значениях, необходимо предсказать последующие десять значений.
Решения показаны на рис. 19.
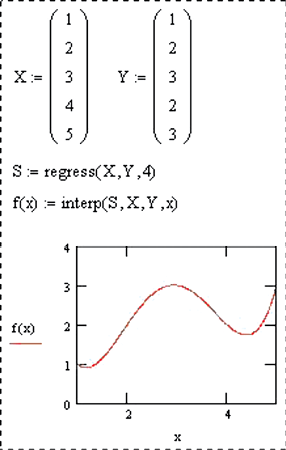
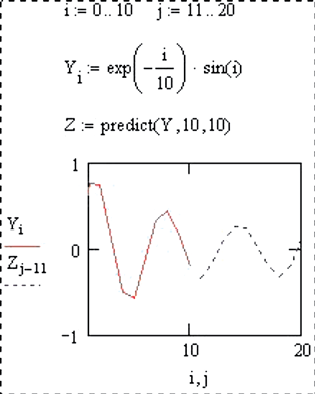
а б
Рис. 19. Решения в MathCAD первой (а) и второй (б) задач
Нахождение корней полинома
polyroots(V) – возвращает вектор, содержащий все корни полинома a0 + a1x + a2x2 + … + akxk, заданного вектором-столбцом коэффициентов
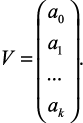
Прочие функции
max(G1,G2,…) – максимальное значение среди аргументов;
min(G1,G2,…) – минимальное значение среди аргументов;
if(a,b,c) – возвращает b, если a ≠ 0, иначе возвращает c;
sign(a) – возвращает –1, 0 или 1 в зависимости от знака числа a.
На рис. 20 показан пример применения функции if.
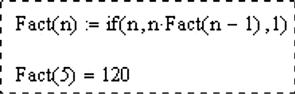
Рис. 20. Функция, вычисляющая факториал

 Если не указано или Нет,
Если не указано или Нет,
 arcsin(1) # пи/2
1.5707963267948966
>>> np.arcsin(-1) # -pi/2
-1,5707963267948966
>>> np.arcsin(0)
0,0
arcsin(1) # пи/2
1.5707963267948966
>>> np.arcsin(-1) # -pi/2
-1,5707963267948966
>>> np.arcsin(0)
0,0