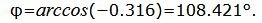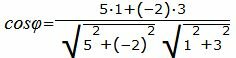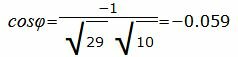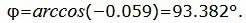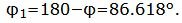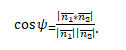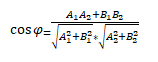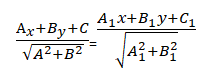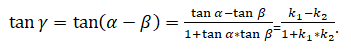Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
 , |
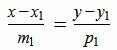(1.1) |
 , |
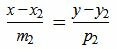(1.2) |
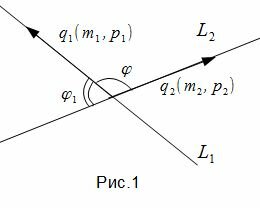
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
,
 , |
(1.3) |
Из выражения (1.3) получим:
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
 . |
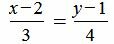(1.5) |
 . |
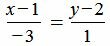(1.6) |
.
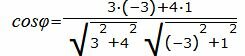
Упростим и решим:
.
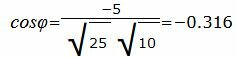
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
Угол между прямыми равен:
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
 . |
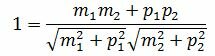(1.7) |
Сделаем преобразования с выражением (1.7):
,
,
,
,
 . |
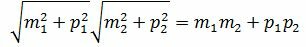
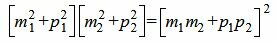
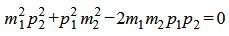
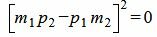
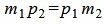(1.8) |
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
 . |
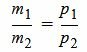(1.9) |
Пример 2. Определить, параллельны ли прямые
 . |
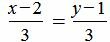(1.10) |
 . |
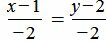(1.11) |
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
 . |
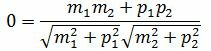(1.12) |
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
 . |
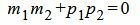(1.13) |
Пример 3. Определить, перпендикулярны ли прямые
 |
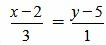(1.14) |
 . |
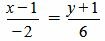(1.15) |
 . |
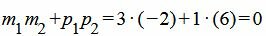(16) |
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
 |
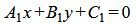(1.17) |
 . |
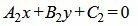(1.18) |
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
.
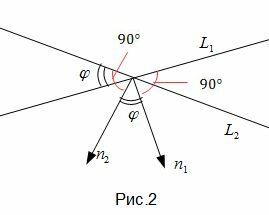
Из определения скалярного произведения двух векторов, имеем:
 . |
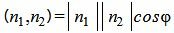(1.19) |
Из уравнения (19) получим
Пример 4. Найти угол между прямыми
 |
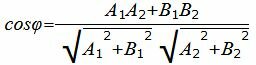(23) |
Упростим и решим:
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
 . |
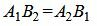(1.24) |
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
 . |
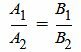(1.25) |
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
 , |
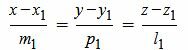(2.1) |
 , |
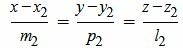(2.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
| , |
(2.3) |
Из выражения (2.3) получим:
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
 . |
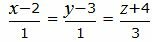(2.5) |
 |
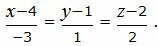(2.6) |
.
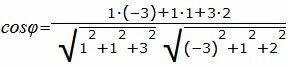
Упростим и решим:
.
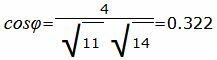
Угол между прямыми равен:
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
| m1=αm2, p1=αp2, l1=αl2 | (2.7) |
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
 |
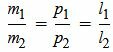(2.8) |
Отметим, что любую пропорцию 
нужно понимать как равенство ad=bc.
Пример 2. Определить, параллельны ли прямые
 . |
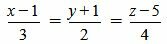(2.9) |
 . |
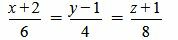(2.10) |
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
 . |
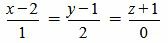(2.11) |
 . |
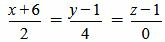(2.12) |
 . |
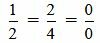(2.13) |
Выражение (2.13) нужно понимать так:
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
 . |
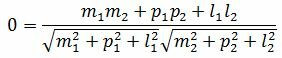(2.15) |
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
 . |
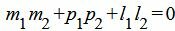(2.16) |
Пример 3. Определить, перпендикулярны ли прямые
 |
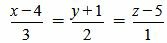(2.17) |
 . |
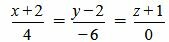(2.18) |
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Угол между прямыми
Определение угла между прямыми
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k 1· k 2 = 0), то прямые перпендикулярны.
Соответственно легко найти угол между прямыми
tg γ = tg ( α — β ) = tg α — tg β 1 + tg α ·tg β = k 1 — k 2 1 + k 1· k 2
Угол между прямыми через направляющие векторы этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано параметрически
x = l t + a y = m t + b
то вектор направляющей имеет вид
Если уравнение прямой задано как
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = — C B значит точка на прямой имеет координаты K(0, — C B ), при y = 0 => x = — C A значит точка на прямой имеет координаты M(- C A , 0). Вектор направляющей KM = .
Если дано каноническое уравнение прямой
то вектор направляющей имеет вид
Если задано уравнение прямой с угловым коэффициентом
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =
Угол между прямыми через векторы нормалей этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано как
то вектор нормали имеет вид
Если задано уравнение прямой с угловым коэффициентом
то вектор нормали имеет вид
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
sin φ = | a · b | | a | · | b |
Примеры задач на вычисления угла между прямыми на плоскости
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ = k 1 — k 2 1 + k 1· k 2 = 2 — (-3) 1 + 2·(-3) = 5 -5 = 1
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор <1; 2>, для второй прямой направляющий вектор
cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2 x + 3 y = 0 => y = — 2 3 x ( k 1 = — 2 3 )
x — 2 3 = y 4 => y = 4 3 x — 8 3 ( k 2 = 4 3 )
tg γ = k 1 — k 2 1 + k 1· k 2 = — 2 3 — 4 3 1 + (- 2 3 )· 4 3 = — 6 3 1 — 8 9 = 18
Угол между прямыми в пространстве
cos φ = | a · b | | a | · | b |
Если дано каноническое уравнение прямой
то направляющий вектор имеет вид
Если уравнение прямой задано параметрически
x = l t + a y = m t + b z = n t + c
то направляющий вектор имеет вид
Решение: Так как прямые заданы параметрически, то <2; 1; -1>- направляющий вектор первой прямой, <1; -2; 0>направляющий вектор второй прямой.
cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор <3; 4; 5>.
Преобразуем второе уравнение к каноническому вид.
1 — 3 y = 1 + y -1/3 = y — 1/3 -1/3
3 z — 5 2 = z — 5/3 2/3
Получено уравнение второй прямой в канонической форме
x — 2 -2 = y — 1/3 -1/3 = z — 5/3 2/3
<-2; — 1 3 ; 2 3 >- направляющий вектор второй прямой.
cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 — 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205
Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
ПРЯМАЯ НА ПЛОСКОСТИ
Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
Показать, при каких условиях прямые на плоскости параллельны, пересекаются, совпадают. Рассмотреть случаи, когда прямые заданы каноническими, общими или уравнениями с угловым коэффициентом. Научить находить косинус угла между пересекающимися прямыми и координаты точки их пересечения. Научить находить расстояние от точки до прямой на плоскости и расстояние между параллельными прямыми.
1) Школьники должны знать:
− условия, при которых прямые пересекаются, параллельны, совпадают, в случаях, если прямые заданы общими уравнениями, каноническими, уравнениями с угловым коэффициентом;
− условия, при которых прямые перпендикулярны;
− формулу для нахождения расстояния от точки до прямой на плоскости;
− формулу для нахождения косинуса угла между пересекающимися прямыми в случаях, если прямые заданы общими уравнениями, каноническими, уравнениями с угловым коэффициентом.
2) Школьники должны уметь:
− выяснять взаимное расположение прямых на плоскости;
− находить угол между прямыми на плоскости;
− находить расстояние от точки до прямой на плоскости;
− находить расстояние между параллельными прямыми на плоскости.
Взаимное расположение прямых на плоскости
Прямые на плоскости могут совпадать, пересекаться или быть параллельными.
1.Пусть на плоскости заданы общими уравнениями две прямые L1 и L2:
где 
и 
– нормальные векторы прямых L1 и L2, соответственно.
а) совпадают, если
− нормальные векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, лежит также и на второй прямой
.
б) параллельны, если
− нормальные векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, не лежит на второй прямой.
.
в) пересекаются, если нормальные векторы прямых не коллинеарны, а значит, их координаты не пропорциональны, т. е.
.
2.Пусть на плоскости заданы прямые L1 и L2 каноническими уравнениями:
а) совпадают, если
− направляющие векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, лежит также и на второй прямой
и 
.
б) параллельны, если
− направляющие векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, не лежит на второй прямой.
и 
.
в) пересекаются, если направляющие векторы прямых не коллинеарны, а значит, их координаты не пропорциональны, т. е.
3.Если прямые L1 и L2 заданы уравнениями с угловым коэффициентом
а) совпадают, если k1 = k2 и b1 = b2;
б) параллельны, если k1 = k2 и b1 ¹ b2;
в) пересекаются, если k1 ¹ k2.
Угол между прямыми на плоскости
Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.
1.Пусть на плоскости заданы прямые L1 и L2 общими уравнениями:
Тогда косинус наименьшего угла между прямыми L1 и L2 на плоскости равен модулю косинуса угла между нормальными векторами этих прямых:
В случае если прямые L1 и L2 перпендикулярны, их нормальные векторы также перпендикулярны, а значит, скалярное произведение нормальных векторов должно быть равно нулю, т. е. 
.
2.Пусть прямые L1 и L2 заданы каноническими уравнениями:
Тогда косинус наименьшего угла между прямыми L1 и L2 равен модулю косинуса угла между направляющими векторами этих прямых:
2. Пусть прямые L1 и L2 заданы уравнениями с угловым коэффициентом
Тогда тангенс наименьшего угла между прямыми L1 и L2 можно найти по формуле:
,
где k1 и k2 – угловые коэффициенты прямых L1 и L2.
Очевидно, что две прямые будут параллельны, если их угловые коэффициенты будут равны.
Итак, условие параллельности двух прямых:
Если две прямые перпендикулярны, т. е. угол φ = p/2, мы получим
Это будет иметь место, когда
Итак, условие перпендикулярности двух прямых:
Расстояние от точки до прямой на плоскости
Расстояние от точки до прямой, не содержащей эту точку, есть длина перпендикуляра, проведенного из этой точки на прямую.
Расстояние от точки до прямой можно вычислить:
1) Как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот;
2) Используя координатно – векторный метод.
Пусть на плоскости заданы прямая L и точка M, не принадлежащая этой прямой
–
расстояние от точки М0(x0, y0) до прямой L.
Замечание. Расстояние между двумя параллельными прямыми на плоскости можно найти по последней формуле, если находить расстояние от любой точки, принадлежащей одной прямой, до другой прямой.
Даны координаты точек A(4, 1), B(2, −1), C(−3, 5). Найти угол между медианой и высотой, проведенными из вершины A.
Напишем уравнение высоты AH. Для любой точки M(x, y), лежащей на прямой AH, вектор 
перпендикулярен вектору 
, а значит, скалярное произведение этих векторов должно быть равно нулю, т. е. 
.
и 
,
Итак, уравнение высоты AH:
Напишем уравнение медианы, проведенной из вершины A. Найдем координаты точки D. Точка D − середина отрезка BC, значит, ее координаты можно найти как среднее арифметическое координат точек B и C. Координаты точек B(2, −1) и C(−3, 5), тогда координаты точки D:
Для любой точки N(x, y), лежащей на медиане AD, вектор 
коллинеарен вектору 
, а значит, координаты этих векторов должны быть пропорциональны. Найдем координаты векторов и :
Запишем условие пропорциональности координат:
(умножим на (1/2));
По свойству пропорций получим:
.
Получили общее уравнение медианы AD:
.
Косинус наименьшего угла между прямыми равен модулю косинуса угла между нормальными векторами этих прямых.
Уравнение прямой AH: Тогда нормальный вектор этой прямой − 
. Уравнение прямой AD: . Тогда нормальный вектор этой прямой − 
.
.
Ответ: 
.
Даны координаты точек A(4, 1), B(2, −1), C(−3, 5). Найти расстояние от точки A до прямой BC.
Напишем уравнение прямой BC. Для любой точки N(x, y), лежащей на прямой BC, вектор 
коллинеарен вектору 
, а значит, координаты этих векторов должны быть пропорциональны:
.
Перемножив по свойству пропорций, перейдем к общему уравнению прямой:
Тогда общее уравнение прямой BC:
.
Точка A(4, 1) 
BC. Расстояние от точки до прямой на плоскости можно найти по формуле:
где 
.
.
Ответ: расстояние от точки A до прямой BC равно 
.
Выяснить взаимное расположение прямых L1 и L2. Если прямые пересекаются, то найти угол между ними и координаты точки их пересечения, а если параллельны, то найти расстояние между ними:
L1: 
;
L2: 
;
Запишем координаты нормальных векторов прямых L1 и L2:
L1: , тогда 
– нормальный вектор прямой L1;
L2: , тогда 
– нормальный вектор прямой L2.
Найдем отношение координат нормальных векторов прямых:
.
Так как координаты нормальных векторов пропорциональны, то векторы 
и 
коллинеарны, а значит, прямые L1, и L2 либо параллельны, либо совпадают.
Прямые параллельны так как
.
Расстояние между прямыми найдем, как расстояние от точки М1, лежащей на прямой L1, до прямой L2 по формуле:
где 
.
Найдем координаты точки M1, принадлежащей прямой L1. Для этого одну из координат, например y0, примем равной нулю, тогда x0 = 4, значит, точка 
.
Ответ: прямые параллельны, расстояние между ними равно 
.
Выяснить взаимное расположение прямых L1 и L2. Если прямые пересекаются, то найти угол между ними и координаты точки их пересечения, а если параллельны, то найти расстояние между ними:
Найдем направляющие векторы прямых L1 и L2:
,
то координаты направляющих векторов не пропорциональны. Следовательно, прямые L1 и L2 пересекаются.
Косинус наименьшего угла между прямыми равен модулю косинуса угла между направляющими векторами этих прямых.
Найдем координаты точки пересечения прямых L1 и L2. Для этого получим общие уравнения этих прямых.
Пусть точка М (x0, y0) − точка пересечения прямых L1 и L2. Тогда координаты точки М должны удовлетворять обоим уравнениям. Решим систему уравнений:
Следовательно, точка 
− точка пересечения прямых L1 и L2.
Ответ: прямые пересекаются, 
, точка пересечения прямых − точка .
Задачи для усвоения пройденного материала.
1. Найти расстояние от точки А(−4, 1) до прямой, проходящей через точки B(1, −1), C(1, 5).
2. Выяснить взаимное расположение прямых 
и 
.
3. Найти точку пересечения медиан треугольника, вершинами которого являются точки 
4. Найти точку пересечения высот треугольника, вершинами которого являются точки
5. Написать уравнение прямой, проходящей через точку 
и составляющей угол 450 с прямой 
.
6. Найти угол между прямыми 
и
1. При каких значениях параметров прямые 
и 
параллельны? совпадают? пересекаются?
2. При каких значениях параметров прямые 
и 
параллельны? совпадают? пересекаются?
3. При каких значениях параметров прямые 
и 
параллельны? совпадают? пересекаются?
4. Как найти угол между пересекающимися прямыми,?
5. Как найти координаты точки пересечения прямых?
6. Как найти расстояние между параллельными прямыми?
7. При каких значениях параметров прямые 
и 
параллельны? совпадают? пересекаются?
http://ru.onlinemschool.com/math/library/analytic_geometry/lines_angle/
http://pandia.ru/text/78/424/22534.php
Условие
коллинеарности двух прямых.
Пусть прямые 
и 
заданные
их общими уравнениями
Две прямые будем
называть коллинеарными, если они либо
параллельны, либо совпадают (сливаются).
Очевидно, что
прямые, определяемые уравнениями (15) и
(16) коллинеарны тогда и только тогда,
когда коллинеарны их нормальные векторы
,
.
Коллинеарность векторов 
означает
существует такого действительного
число 𝜆,
что
Следовательно прямые, заданные уравнениями
(15) и (16), коллинеарны тогда и только
тогда, когда выполнены равенства:
В случае 
,
равенства (17) и (18) могут быть записаны
в виде :
Равенство (19)
является условием коллинеарности
прямых
и
Замечание. В
равенстве (17) мы предполагаем, что
.
Если хотя бы один их коэффициентов 
обращается в ноль, например 
,
то из равенства (17) имеем, что и 
.
Рассмотрим
определитель
Если прямые
и 
не
коллинеарны, то нарушено равенство
(19), тогда очевидно определитель 
.
Заметим, что 
является определителем основной матрицы
системы линейных алгебраических
уравнений
Данная система
имеет единственное решение при условии,
что
и эти решения определяются формулами
Крамера:
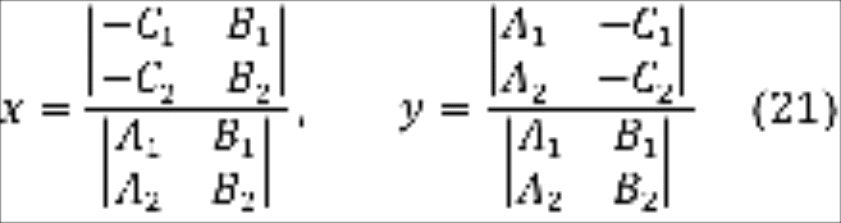
Итак, если прямые,
лежащие в плоскости
неколлинеарны, то координаты точки их
пересечения находятся по формулам (21).
Если выполнено
условие (19), то прямые 
и 
коллинеарны, т.е. они либо параллельны
и не имеют ни одной общей точки, либо
эти прямые совпадают.
Пусть прямые
и
коллинеарны, т.е. выполнено равенство
(19). Обозначим каждое из отношений (19)
через
,
т.е. положим, что 
Тогда справедливы
равенства 
.
Рассмотрим произвольную точку 
,
лежащую на прямой
.
Тогда координаты точки
удовлетворяют
уравнению
Пользуясь равенствами
(23),
получим
Могут представиться
два случая.
-
,
тогда из равенства (24) найдём
.
Из последних соотношений имеем
Следовательно в
случае, когда 
, произвольная точка
прямой
не лежит на прямой
,
т.е. у прямых 
нет общих точек. Следовательно, условие
(25)
является условием
параллельности прямых
.
-
Пусть
теперь
,
где
– величина, указанная в равенствах
(21). Тогда из равенства (24) получим
,
т.е. точка
лежит как на прямой
,
так и на прямой
.
Следовательно эти прямые сливаются.
Итак, мы получили
следующее условие слияния двух прямых
Заметим, что при
выполнении условия (25) система линейных
уравнений (20) не имеет решений, а при
выполнении условия (26) имеет бесконечное
множество решений.
Условие ортогональности
двух прямых.
Любые две
пересекающиеся в одной точке прямые
образуют два угла, в сумме равных 𝜋.
Один из указанных углов совпадает с
углом между нормальными векторами 
и 
этих
прямых.
Найдём угол между
векторами
и 
Пусть прямые
заданы их общими уравнениями (15) и (16),
тогда 
,
.
Обозначим через 
угол между векторами
и 
Косинус этого угла может быть вычислен
по формуле:
Учитывая в этой
формуле, что
,
,
получим
В частности, если
угол
прямой, то 
и мы получим условие ортогональности
прямых
(28)
Пусть теперь прямые
заданы их уравнениями с угловыми
коэффициентами
Запишем уравнения
(27) и (28) в виде
Уравнения (31) и
(32) являются общими уравнениями прямых
при 
,
,
,
,
,
.
При этом из условия (25) получим условие
параллельности прямых 
Из условия (26)
получим условие слияния двух прямых
.
Из формулы (27)
получим формулу для определения угла
между прямыми
Из условия (28)
получим условие ортогональности прямых
Рассмотрим теперь
случай, когда прямые
заданы их каноническими уравнениями.
Из уравнений (37) и
(38) получим
Уравнения (39) и
(40) являются общими уравнениями прямых
при 
.
Тогда из условий (25), (26), (27), (28) получим
-
Условие
коллинеарности
. -
Условие
параллельности
. -
Условие
слияния
. -
Формула
для вычисления угла
. -
Условие
ортогональности
.
Приведём ещё одну
формулу для нахождения угла между двумя
прямыми.
Пусть прямые
заданы уравнениями
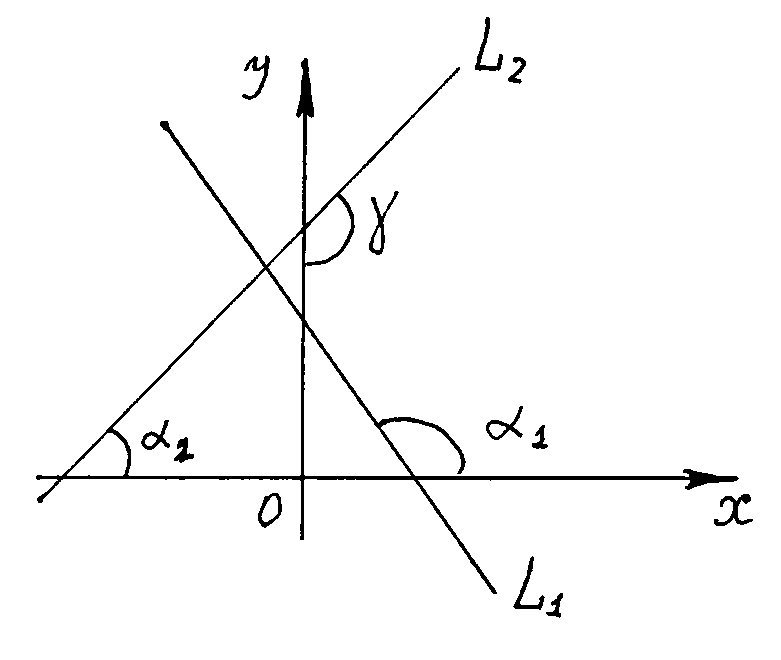
Пусть 
— угол между прямыми
,
отсчитанный от прямой 
до
прямой
против часовой стрелки. Тогда 
,
либо 
,
либо 
.
Но во всех указанных случаях 
.
Учитывая в последнем равенстве, что
,
,
получим
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
14.11.201995.23 Кб01.doc
- #
03.08.2019142.65 Mб191.doc
- #
26.09.201950.69 Кб01.doc
- #
09.02.201529.7 Кб81.doc
- #
24.09.2019146.43 Кб01.doc
- #
27.09.2019321.02 Кб21.doc
- #
13.09.2019314.37 Кб01.doc
Задача 66467 Математика .
Даны уравнения двух…
Условие
Математика .
Даны уравнения двух прямых. Найдите: а) косинус угла между ними; б) точку их пересечения . 2) x–3y–1=0 , x+y–1=0
математика колледж
426
Решение
★
1)
x–3y–1=0 ⇒ vector{n_(1)}=(1;-3)
x+y–1=0 ⇒ vector{n_(2)}=(1;1)
По формуле ( см. приложение)
cos φ = vector{n_(1)}* vector{n_(2)}/| (vector{n_(1)}|*| vector{n_(2)})
vector{n_(1)}* vector{n_(2)}=1*1+(-3)*1=-2
| (vector{n_(1)}|=sqrt(1^2+(-3)^2)=sqrt(10)
| vector{n_(2)}|=sqrt(1^2+1^1=sqrt(2)
cos φ =-2/)sqrt(10)*sqrt(2)=-sqrt(2)/sqrt(10)=-sqrt(1/5)
φ — тупой угол, а смежный с ним острый
cos(180- φ )=1/sqrt(5)
угол между прямыми
arccos(1/sqrt(5))
О т в е т. arccos(1/sqrt(5))
2)
Чтобы найти точку пересечения прямых решаем систему уравнений
{x–3y–1=0
{x+y–1=0
Применяем способ подстановки
{x–3(1-х)–1=0
{y=1-x и подставляем в первое уравнение
{x–3+3х–1=0
{y=1-x
{4х=4
{y=1-x
{х=1
{y=1-1
{х=1
{y=0
О т в е т. (1;0)
Написать комментарий
Определение угла между скрещивающимися прямыми
Пересечение двух линий на плоскости говорит о наличии у них одной общей точки. Она же является центром их пересечения и делит их на лучи.
Лучи формируют четыре угла, которые являются неразвернутыми. Зная о размере одного из них, можно вычислить значение и остальных. Точно можно утверждать, что если один из них – прямоугольный, то остальные три равнозначны ему, а линии будут перпендикулярными.
Рис. 1 Графическое отображение пересечения прямых
Как найти угол между скрещивающимися прямыми
Для определения угла между двумя скрещивающимися линиями можно воспользоваться специальным онлайн-калькулятором или применить традиционный математический алгоритм для вычислений.
Предположим, что две бесконечные линии задаются уравнениями общего вида:
A1 + B1 + C1 = 0
A2 + B2 + C2 = 0
Искомое значение следует обозначить как φ. Численная величина угла измеряется в градусах от 0 до 90°, т. е. угол будет острым или прямоугольным. Необходимо ввести еще одно понятие– угол ψ между нормальными векторами данных прямых:
Если он меньше, либо равен 90°, то непосредственно сам искомый угол будет соответствовать его градусной мере. В случае когда ψ больше 90°, для вычисления φ необходимо применить известную формулу:
φ = 1800 — ψ.
Для обоих вариантов достоверно утверждение, что cos φ = lcos ψl. Выполнив необходимые вычисления, можно рассчитать искомое значение:
Если по условию задачи существует некий прямоугольный треугольник с известными сторонами, расположенными на двух прямых, то для вычисления угла между этими прямыми необходимо знать синус, тангенс и косинус искомого угла.
Для нахождения значения синуса угла, образованного в результате пересечения двух прямых, вычисляют модуль косинуса этого угла, образованного направляющими векторами данных прямых.
Пример решения задачи
На школьных уроках геометрии для решения в классе часто предлагается следующий вид задач по поиску угла между двумя прямыми.
Ниже приведем алгоритм решения задачи, при которой бесконечные линии на плоскости заданы уравнениями общего вида, в которых присутствует угловой коэффициент.
Обозначим прямые как (L1) и (L2). Каждая из них задается уравнением следующего вида:
А1х + В1у + С1 = 0;
А2х + В2у + С2 = 0;
Зная, что нормальные вектора каждой из них имеют вид:
Суть задачи сводится к вычислению угла φ, образованного нормальными векторами.
Используем определение скалярного произведения векторов:
и координатное выражение их длин, а также их скалярное произведение:
В практических задачах по математике часто требуется найти не сам угол между пресекающимися прямыми, а составить уравнение их всех, при условии, что прямые пересекаются между собой.
Так, если прямые заданы уравнениями общего вида с коэффициентами, то
Последнее равенство часто называют уравнением биссектрис углов, образованных в результате пересечения прямых. Понятие «биссектриса» в геометрии — это некое геометрическое место точек, которые удалены на одинаковое расстояние от сторон угла.
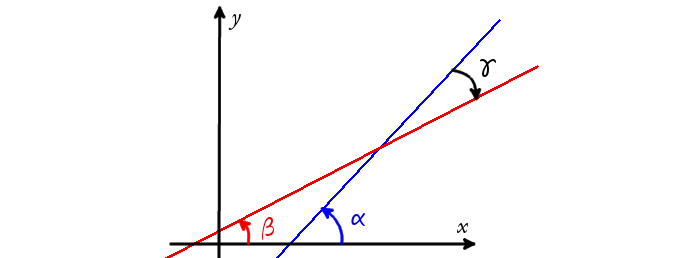
Если прямые задаются уравнениями, включающими угловой коэффициент, который определяется тангенсом угла, найти значение углов, образованных при их пересечении, достаточно просто:
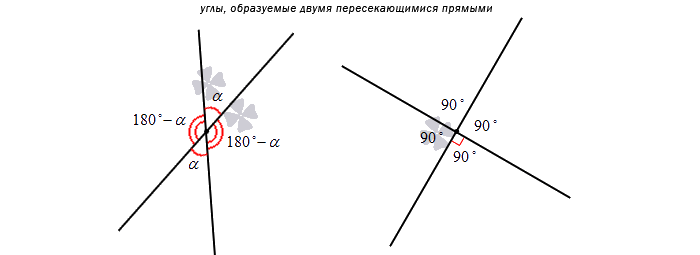
Рис. 2 Углы, образованные пересечением двух прямых на плоскости
tan α = k1;
tan β = k2;
где k1 и k2 – те самые угловые коэффициенты.
Следовательно, чтобы вычислить значение γ, следует применить формулы:
γ = α — β
tan γ = tan (α — β)
Решение очевидно:
Как найти косинус
Косинус является одной из основных тригонометрических функций. Согласно определения данная величина представляет численное выражение отношения прилежащего катета (в прямоугольном треугольнике) к гипотенузе. Для нахождения величины cos угла можно воспользоваться данными о сторонах треугольника, формулами приведения или же тригонометрическими тождествами. С каждым из способов более подробно познакомимся далее.
1
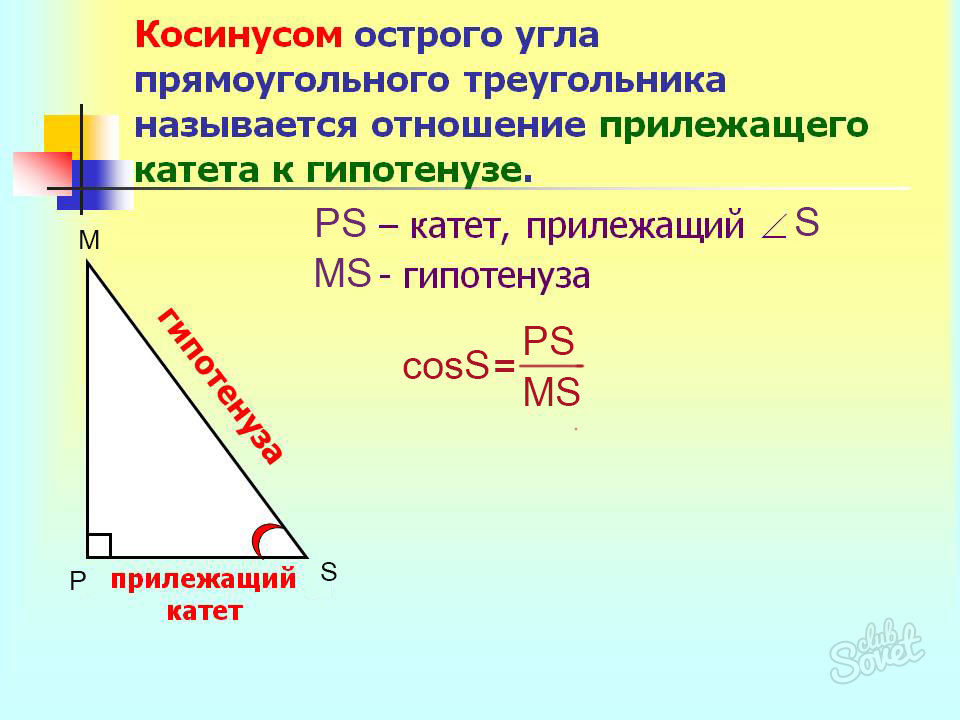
Нахождение величины косинуса по определению
Определение косинуса “привязывает” данную тригонометрическую функцию с прямоугольному треугольнику. Итак, перед вами указанная фигура – треугольник MSP, ∠P = 90°. Тогда:
- cosM = MP/MS,
- cosS = PS/MS, где
- MP и PS – прилежащие (для каждого конкретного угла) катеты,
- MS – гипотенуза заданного треугольника.
2
Нахождение величины косинуса угла между векторами
Пересечение направленных отрезков прямой – векторов – ведет к образованию углов. Найти их косинус (а, значит, в последствии и градусную меру) позволяет определение скалярного произведения векторов. Данная формулировка предполагает перемножение длин векторов на косинус угла, образованного в результате их пересечения. Т.о., если у вас есть 2 направленных отрезка ū и ō, то
- ūō = ū *ō = (ū, ō) = lūl * lōl * cos (ū,ˆ ō), ⇒
- cos (ū,ˆ ō) = (ū, ō) / lūl * lōl.
- В проекции на координаты декартовой системы направленные отрезки имеют параметры ū (x,y) = (u(x) ,u(y)) и ō (x,y) = (o(x), o(y)). Значит соотношение приобретает следующий вид:
- cos (ū,ˆ ō) = (u(x)*o(x) + u(y)*o(y)) / lūl * lōl = (u(x)*o(x) + u(y)*o(y)) / (√(u(x)2 + u(y)2) * √o(x)2 + o(y)2).
Если направленные отрезки заданы не на плоскости, а в пространстве, добавляется третья координата – z. Выражение нахождения косинуса преобразуется и будет иметь следующий вид:
cos (ū,ˆ ō) = (u(x)*o(x) + u(y)*o(y) + u(z)*o(z)) / lūl * lōl = (u(x)*o(x) + u(y)*o(y) + u(z)*o(z)) / (√(u(x)2 + u(y)2 + u(z)2) * √o(x)2 + o(y)2 + o(z)2.
3
Нахождение величины косинуса с помощью формул приведения
Работая с формулами приведения для косинуса, необходимо понимать и помнить важное правило – переход от функции к кофункции (в данном случае переход от cos к sin) происходит при 90° и 270°. При 180° и 360° такой трансформации не будет. Исходя из этого, справедливыми будут следующие соотношения:
- cos(π/2 – μ) = sinμ,
- cos(π/2 + μ) = -sinμ,
- cos(π – μ) = cos(π + μ) = -cosμ,
- cos(3π/2 – μ) = -sinμ,
- cos(3π/2 + μ) = sinμ,
- cos(2π – μ) = cos(2π + μ) = cosμ, где
- μ – угол поворота.
Т.к. косинус является периодической функцией с периодом 2πk, где k – произвольное целое значение, в общем случае выражения приведения приобретут следующий вид:
- cos(μ + 2πk) = cos(-μ + 2πk) = cosμ,
- cos(π/2 – μ + 2πk) = sinμ,
- cos(π/2 + μ + 2πk) = -sinμ,
- cos(π – μ + 2πk) = cos(π + μ + 2πk) = -cosμ,
- cos(3π/2 – μ + 2πk) = -sinμ,
- cos(3π/2 + μ + 2πk) = sinμ,
- cos(2π – μ + 2πk) = cos(2π + μ + 2πk) = cosμ.
4
Нахождение величины косинуса через тригонометрические тождества
Данные тождества представляют собой выражения (равенства), справедливые для угла любой градусной меры.
- cos2μ + sin2μ = 1 ⇒ cos2μ = 1 – sin2μ ⇒ cosμ = ±√ 1 – sin2μ
- tgμ = sinμ / cosμ ⇒ cosμ = sinμ / tgμ
- ctgμ = cosμ / sinμ ⇒ cosμ = ctgμ * sinμ
- 1/cos2μ = tg2μ + 1 ⇒ cos2μ = 1 / (tg2μ + 1) ⇒ cosμ = ± 1 / √tg2μ + 1
5
Нахождение косинуса угла – табличные величины
Для каждого угла, градусная мера которого находится в промежутке от 0° до 360°, можно определить соответствующее значение косинуса, воспользовавшись одноименной таблицей. Наиболее распространенными и часто используемыми являются следующие константы:
- cos0° = 1, cos90° = 0,
- cos30° = √3/2, cos180° = -1,
- cos60° = 1/2, cos360° = 1.
- cos45° = √2/2,
