Содержание:
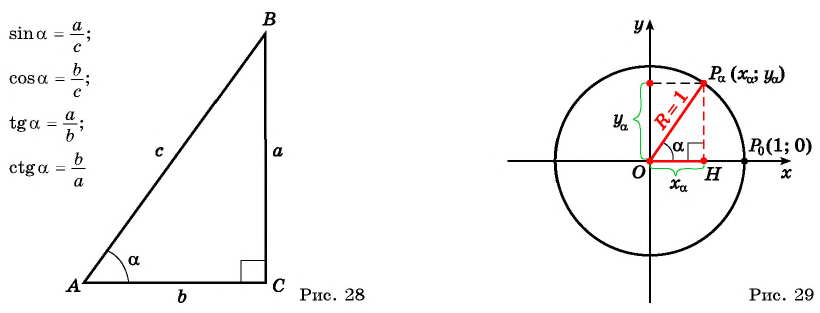
При изучении геометрии вы рассматривали отношения сторон в прямоугольном треугольнике и познакомились с понятиями синуса, косинуса, тангенса и котангенса острого угла (рис. 28).
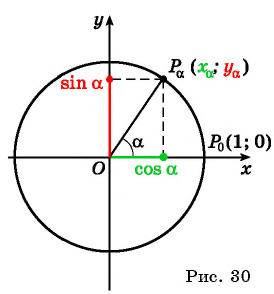
Построение синуса и косинуса произвольного угла
Построим точку
Рассмотрим прямоугольный треугольник 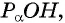
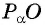
Таким образом, синус угла 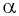
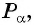
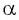
Поскольку в тригонометрии рассматриваются углы 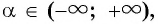
Определение синуса произвольного угла
Определение:
Синусом угла 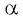
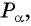
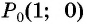
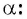
Определение косинуса произвольного угла
Определение:
Косинусом угла 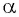
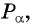
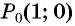
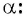
Для того чтобы найти синус и косинус произвольного угла 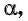
- Построить точку
единичной окружности.
- Найти ординату точки
- Найти абсциссу точки
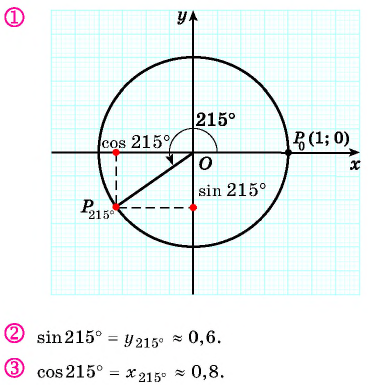
Найдите синус и косинус угла
Значения синуса и косинуса произвольного угла с помощью единичной окружности в основном можно указать только приближенно.
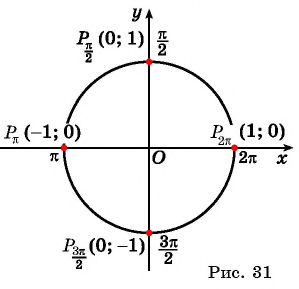
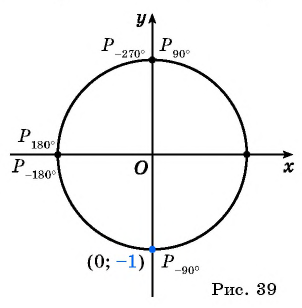
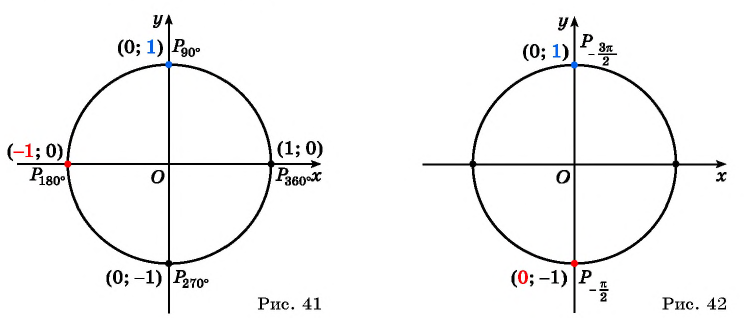
Однако для некоторых углов значения синуса и косинуса можно указать точно. Определим значения синуса и косинуса для углов, которые соответствуют точкам пересечения окружности с осями координат 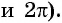
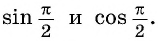
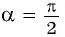
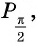
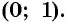
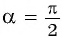
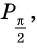
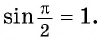
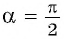
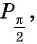
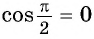
Пользуясь определением синуса и косинуса угла 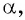
Так как ординаты и абсциссы точек единичной окружности изменяются от -1 до 1, то значения синуса и косинуса произвольного угла принадлежат промежутку
Например, выясним, может ли 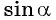
Значения синуса произвольного угла принадлежат отрезку 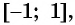
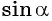
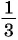
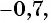
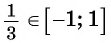
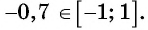
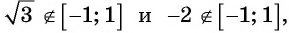
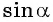
По определению синуса и косинуса угла 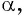
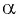
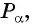
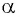
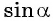
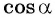
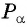
Пример №1
Определите знак выражения:
Решение:
а) Так как 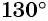
б) Так как 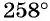
в) Так как 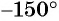
г) Так как 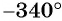
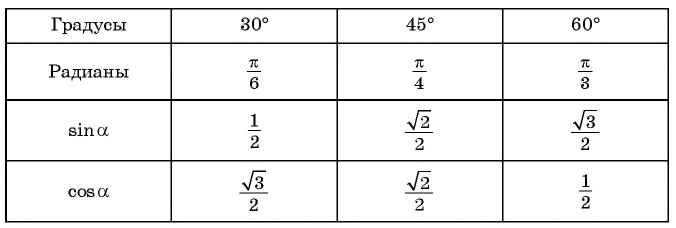
Из геометрии нам известны значения синусов и косинусов острых углов (см. табл.).
С помощью этих значений можно находить значения синусов и косинусов некоторых других углов
Пример №2
Вычислите:
Решение:
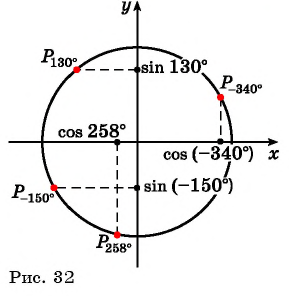
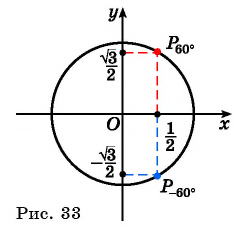
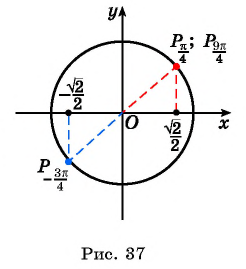
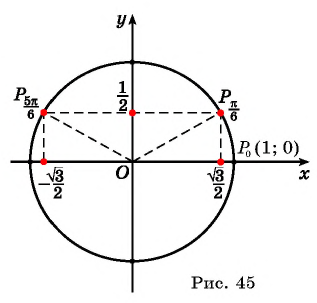
а) Отметим на единичной окружности точку 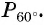
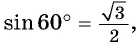
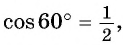
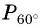
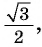
Точки 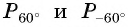
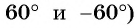
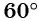
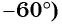
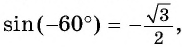
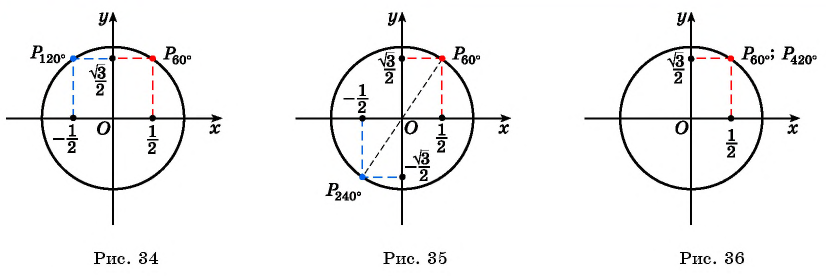
б) Так как 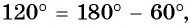
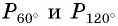
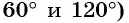
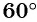
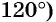
в) Точки 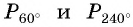
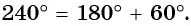
г) Поскольку 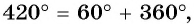
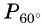
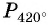
Пример №3
Вычислите:
Решение:
а) Так как 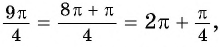
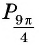
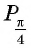
Поскольку
б) Точки 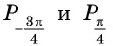
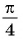
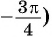
Пример №4
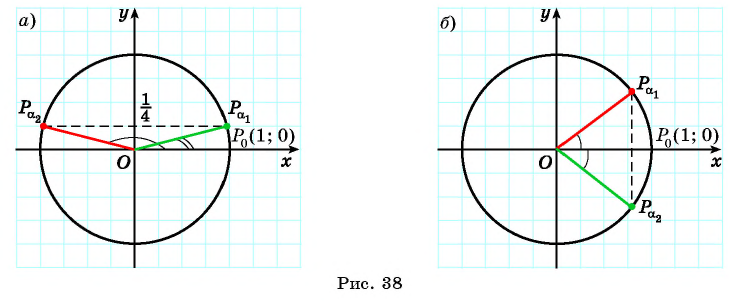
Постройте один из углов, если:
Решение:
а) Так как 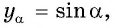
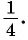
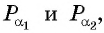
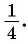
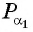
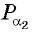
б) Так как 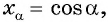
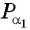
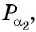
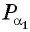
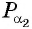
- Заказать решение задач по высшей математике
Примеры заданий и их решения:
Пример №5
Точка 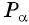
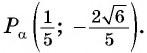
Решение:
Синусом угла 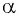
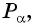
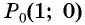
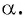
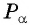
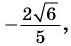
Косинусом угла 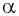
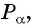
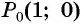
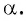
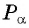
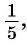
Пример №6
Если 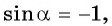
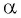
Выберите правильный ответ.
Решение:
Так как синусом угла 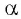
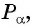
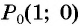
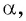
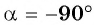
Пример №7
Если 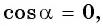
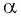
Выберите правильный ответ.
Решение:
Так как косинусом угла 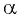
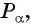
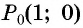
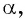
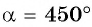
Пример №8
Найдите значение выражения:
Решение:
а) Абсцисса точки 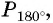
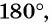
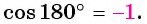
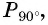
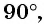

б) 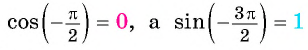
Может ли 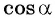
Решение:
Поскольку
а) не может быть равным 1,2, так как
б) может быть равным 0,89, так как
в) не может быть равным 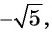
г) может быть равным 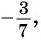
Пример №9
Определите знак выражения:
Решение:
а) 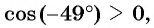
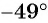
б) 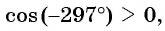
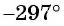
в) 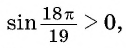
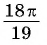
г) 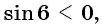
Пример №10
Сравните:
Решение:
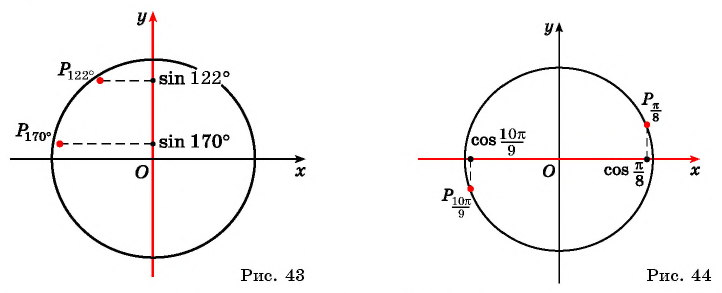
а) Отметим на единичной окружности точки, соответствующие углам 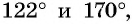
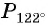
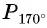
б) Сравним абсциссы точек единичной окружности 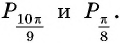
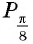
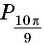
Пример №11
С помощью единичной окружности найдите значение:
Решение:
а) Ордината точки 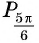
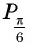
б) Абсцисса точки 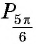
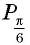
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
Угол между векторами.
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Как найти косинус угла между векторами
Формула
Чтобы найти косинус угла между векторами нужно, скалярное произведение этих векторов разделить на произведение их длин.
Примеры вычисления косинуса угла между векторами
Задание. Найти косинус угла $phi$ между векторами $bar=(4 ;-3)$ и $bar=(1 ;-2)$
Решение. Так как векторы заданы на плоскости, воспользуемся формулой
Ответ. $cos phi=frac<2 sqrt<5>><5>$
Задание. Найти косинус угла между векторами $bar=(3 ;-4 ; 0)$ и $bar=(4 ;-4 ;-2)$, заданных в пространстве.
Решение. Для нахождения косинуса угла между заданными векторами, воспользуемся формулой
Подставляя координаты векторов $bar$ и $bar$, получим
Ответ. $begin cos phi=frac<14> <15>end$
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/
http://www.webmath.ru/poleznoe/formules_13_9.php
Содержание:
- Формула
- Примеры вычисления косинуса угла между векторами
Формула
Чтобы найти косинус угла между векторами нужно,
скалярное произведение этих векторов
разделить на произведение их длин.
В случае если векторы заданны на плоскости и имеют координаты $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, то косинус между ними вычисляется по формуле:
$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}}}$$
Если же векторы заданы в пространстве, то есть
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то косинус угла вычисляется по формуле
$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
Примеры вычисления косинуса угла между векторами
Пример
Задание. Найти косинус угла $phi$ между векторами
$bar{a}=(4 ;-3)$ и $bar{b}=(1 ;-2)$
Решение. Так как векторы заданы на плоскости, воспользуемся формулой
$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}}}$
Подставим координаты заданных векторов:
$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{4 cdot 1+(-3) cdot(-2)}{sqrt{4^{2}+(-3)^{2}} sqrt{1^{2}+(-2)^{2}}}=$$
$$=frac{4+6}{sqrt{16+9} sqrt{1+4}}=frac{10}{sqrt{25} sqrt{5}}=frac{10}{5 sqrt{5}}=frac{2 sqrt{5}}{5}$$
Ответ. $cos phi=frac{2 sqrt{5}}{5}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти косинус угла между векторами
$bar{a}=(3 ;-4 ; 0)$ и $bar{b}=(4 ;-4 ;-2)$, заданных в пространстве.
Решение. Для нахождения косинуса угла между заданными векторами, воспользуемся формулой
$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} cdot sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
Подставляя координаты векторов $bar{a}$ и $bar{b}$, получим
$$begin{aligned} cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{3 cdot 4+(-4) cdot(-4)+0 cdot(-2)}{sqrt{3^{2}+(-4)^{2}+0^{2}} sqrt{4^{2}+(-4)^{2}+(-2)^{2}}} &=\=frac{12+16+0}{sqrt{9+16+0} sqrt{16+16+4}}=frac{28}{sqrt{25} sqrt{36}}=frac{28}{5 cdot 6}=frac{14}{15} end{aligned}$$
Ответ. $begin{aligned} cos phi=frac{14}{15} end{aligned}$
Читать дальше: как найти скалярное произведение векторов.
Мы уже находили косинусы углов треугольника по его сторонам в произвольном треугольнике и косинус острого угла прямоугольного треугольника.
Рассмотрим, как найти косинусы углов треугольника по его вершинам.
Задача
Дано: ΔABC,
A(-2;0), B(6;1), C(-3;-5).
1) Найти косинусы углов треугольника ABC;
2) Определить вид треугольника.
Решение:
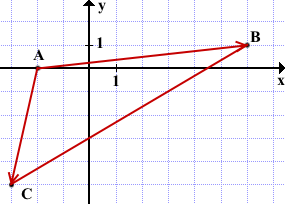
(Чертёж не обязательно делать на координатной плоскости. Достаточно выполнить его схематически, для упрощения понимания, какой угол какими векторами образован).
Следовательно,
Найдём координаты векторов:
Находим скалярное произведение векторов:
Поскольку скалярное произведение меньше нуля, угол, образованный данными векторами, тупой. Значит треугольник ABC — тупоугольный.
Длины (или модули) векторов:
Отсюда
2) Угол B образован векторами
Таким образом,
Так как
— противоположные векторы, то их координаты отличаются только знаками и векторы имеют одинаковую длину:
3) Угол C образован векторами
Ответ:
ΔABC — тупоугольный.

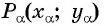
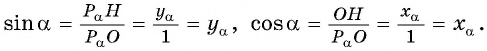
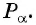
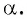
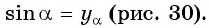
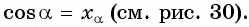
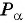 единичной окружности.
единичной окружности.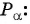
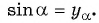
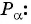
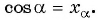
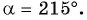
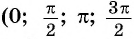
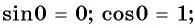
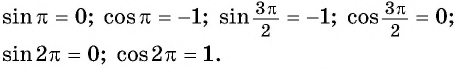
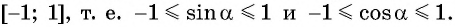
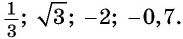
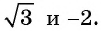
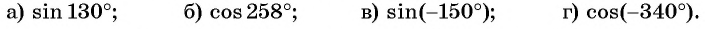
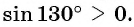
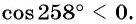
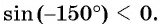
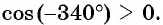
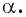
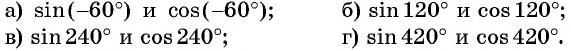
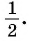
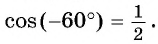
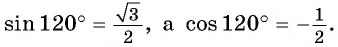
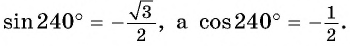
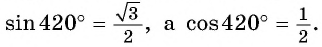

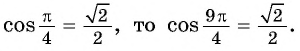
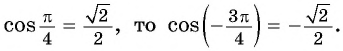

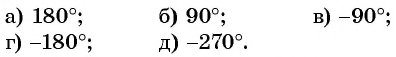
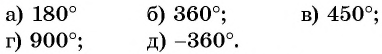
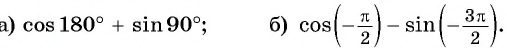
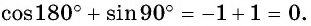
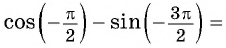
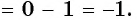

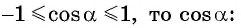
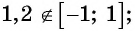
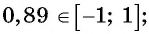
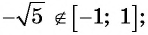
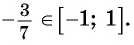
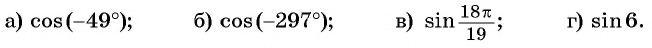
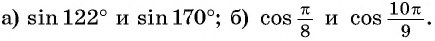
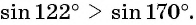
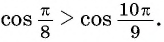

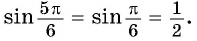
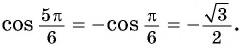



![Rendered by QuickLaTeX.com [cos A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}}.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-e8689674e5f3124a8a7b97118aa3fac5_l3.png)
![Rendered by QuickLaTeX.com [cos B = frac{{overrightarrow {BA} cdot overrightarrow {BC} }}{{left| {overrightarrow {BA} } right| cdot left| {overrightarrow {BC} } right|}}.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-84cec08df9d53766e4ee96ddaaf275bb_l3.png)
![Rendered by QuickLaTeX.com [cos C = frac{{overrightarrow {CA} cdot overrightarrow {CB} }}{{left| {overrightarrow {CA} } right| cdot left| {overrightarrow {CB} } right|}}.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-22361638670683db4b7ed7317c63bb72_l3.png)