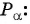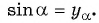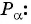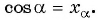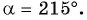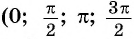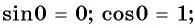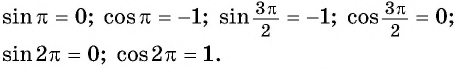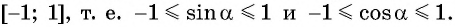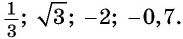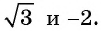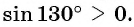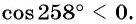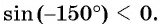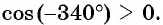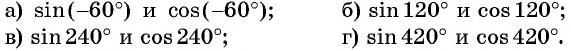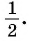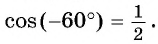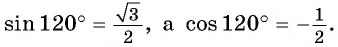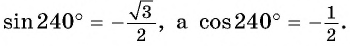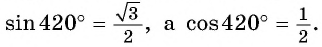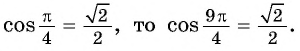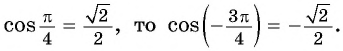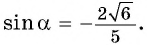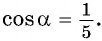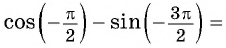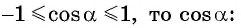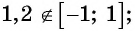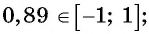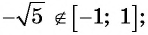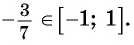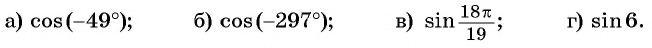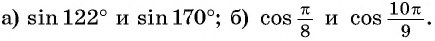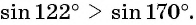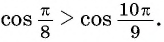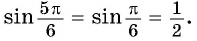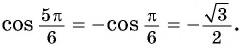Чтобы найти косинус угла по клеточкам, следует вспомнить, что это собственно за величина — косинус.
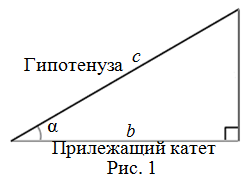
По определению, косинус — это отношение прилежащего катета к гипотенузе.
Зная это определение мы очень легко можем найти косинус любого прямоугольного треугольника, нарисованного на клеточках. То есть если задан просто угол, мы достраиваем его до прямоугольного треугольника:
Разберем несколько случаев.
Катеты расположены вертикально и горизонтально. Тогда их длину определяем по клеточкам, а длину гипотенузы по теореме Пифагора.
Катеты расположены произвольно. Заключаем треугольник в прямоугольник и находим катеты и гипотенузу по теореме Пифагора для всех трех сторон. Дальше находим косинус как отношение по определению.
Например здесь катет АО находится как корень из 20 (16+4). Гипотенуза ОВ находится как корень из 37 (36+1). Их отношение — косинус угла АОВ.
Если треугольник АОВ не получается прямоугольным, то имеет смысл использовать теорему косинусов:
Содержание:
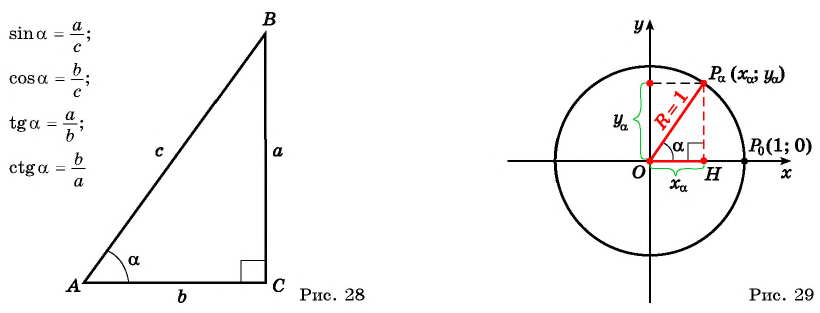
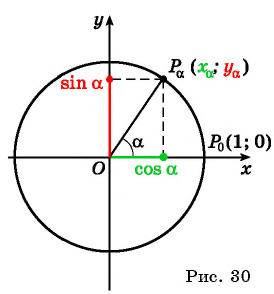
При изучении геометрии вы рассматривали отношения сторон в прямоугольном треугольнике и познакомились с понятиями синуса, косинуса, тангенса и котангенса острого угла (рис. 28).
Построение синуса и косинуса произвольного угла
Построим точку
Рассмотрим прямоугольный треугольник 
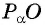
Таким образом, синус угла 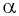
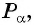
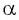
Поскольку в тригонометрии рассматриваются углы 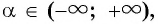
Определение синуса произвольного угла
Определение:
Синусом угла 
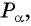
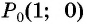
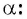
Определение косинуса произвольного угла
Определение:
Косинусом угла 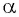
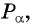
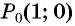
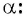
Для того чтобы найти синус и косинус произвольного угла 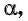
- Построить точку
единичной окружности.
- Найти ординату точки
- Найти абсциссу точки
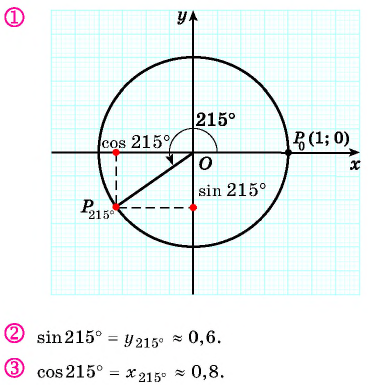
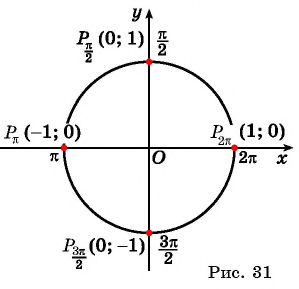
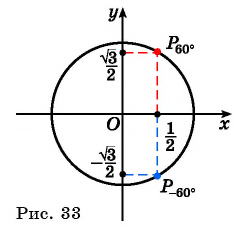
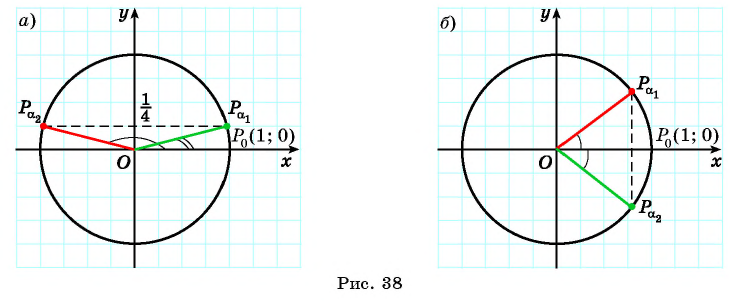
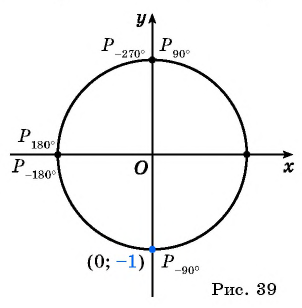
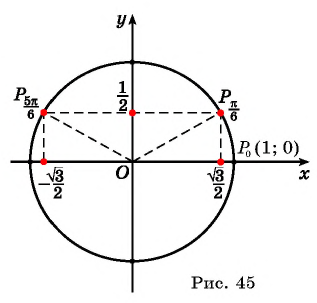
Найдите синус и косинус угла
Значения синуса и косинуса произвольного угла с помощью единичной окружности в основном можно указать только приближенно.
Однако для некоторых углов значения синуса и косинуса можно указать точно. Определим значения синуса и косинуса для углов, которые соответствуют точкам пересечения окружности с осями координат 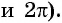
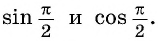
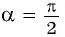
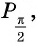
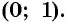
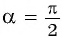
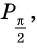
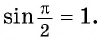
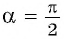
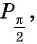
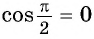
Пользуясь определением синуса и косинуса угла 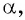
Так как ординаты и абсциссы точек единичной окружности изменяются от -1 до 1, то значения синуса и косинуса произвольного угла принадлежат промежутку
Например, выясним, может ли 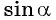
Значения синуса произвольного угла принадлежат отрезку 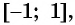
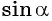
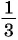
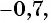
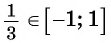
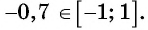
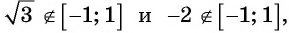
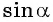
По определению синуса и косинуса угла 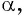
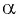
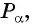
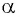
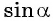
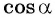
Пример №1
Определите знак выражения:
Решение:
а) Так как 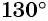
б) Так как 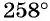
в) Так как 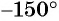
г) Так как 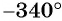
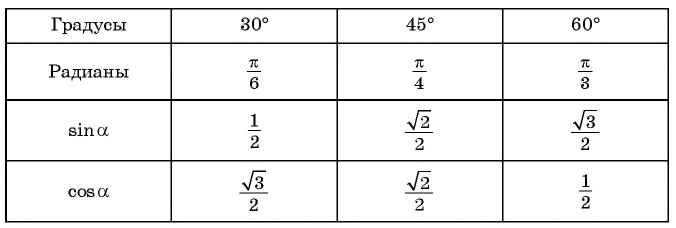
Из геометрии нам известны значения синусов и косинусов острых углов (см. табл.).
С помощью этих значений можно находить значения синусов и косинусов некоторых других углов
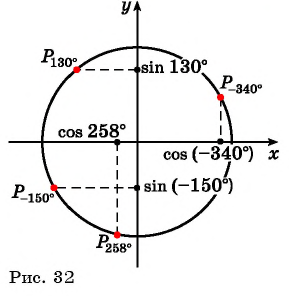
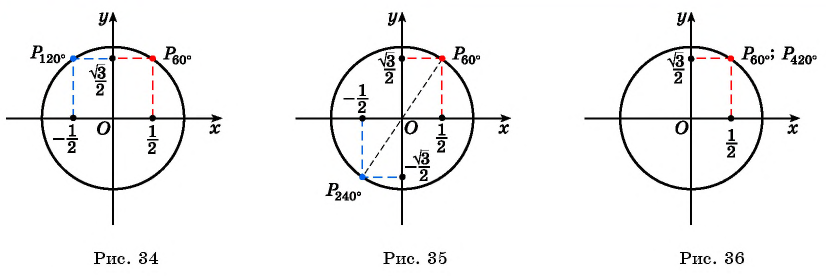
Пример №2
Вычислите:
Решение:
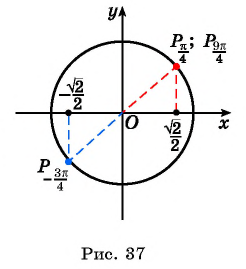
а) Отметим на единичной окружности точку 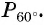
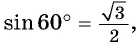
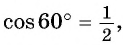
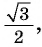
Точки 
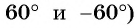
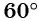
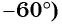
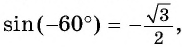
б) Так как 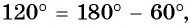
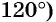
в) Точки 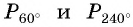
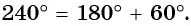
г) Поскольку 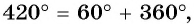
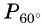
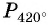
Пример №3
Вычислите:
Решение:
а) Так как 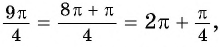
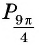
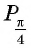
Поскольку
б) Точки 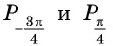
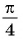
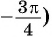
Пример №4
Постройте один из углов, если:
Решение:
а) Так как 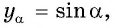
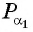
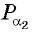
б) Так как 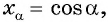
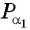
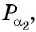
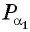
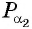
- Заказать решение задач по высшей математике
Примеры заданий и их решения:
Пример №5
Точка 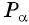
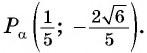
Решение:
Синусом угла 
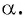
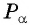
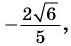
Косинусом угла 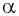
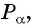
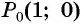
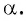
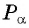
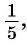
Пример №6
Если 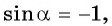
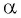
Выберите правильный ответ.
Решение:
Так как синусом угла 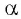
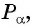
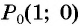
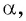
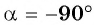
Пример №7
Если 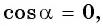
Выберите правильный ответ.
Решение:
Так как косинусом угла 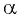
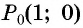
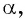
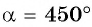
Пример №8
Найдите значение выражения:
Решение:
а) Абсцисса точки 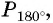
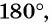
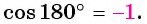
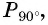
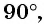

б) 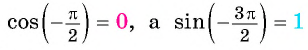
Может ли 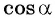
Решение:
Поскольку
а) не может быть равным 1,2, так как
б) может быть равным 0,89, так как
в) не может быть равным 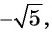
г) может быть равным 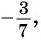
Пример №9
Определите знак выражения:
Решение:
а) 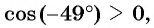
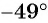
б) 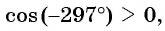
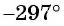
в) 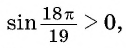
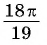
г) 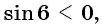
Пример №10
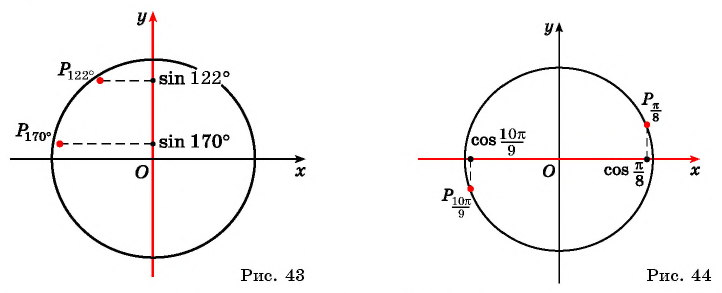
Сравните:
Решение:
а) Отметим на единичной окружности точки, соответствующие углам 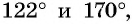
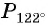
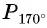
б) Сравним абсциссы точек единичной окружности 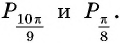
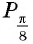
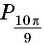
Пример №11
С помощью единичной окружности найдите значение:
Решение:
а) Ордината точки 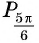
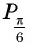
б) Абсцисса точки 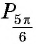
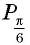
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
Содержание:
- Косинус угла в треугольнике
- Косинус произвольного угла
Косинус угла в треугольнике
Определение
Косинус острого угла прямоугольного треугольника — это отношение прилежащего к
этому углу катета к гипотенузе (рис. 1):
$cos alpha=frac{b}{c}$
Пример
Задание. Найти косинус острого угла прямоугольного треугольника, если его гипотенуза равна 5 см,
а прилежащий катет — 4 см.
Решение. Согласно определению
$cos alpha=frac{4}{5}$
Ответ. $cos alpha=frac{4}{5}$
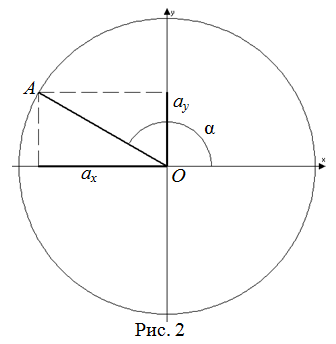
Косинус произвольного угла
Определение
Косинусом произвольного угла
$alpha$, образованного осью абсцисс и произвольным радиус-вектором
$overline{O A}=left(a_{x} ; a_{y}right)$ (рисунок 2), называется отношение
проекции этого вектора на ось
$Ox$ к его длине
$a=|overline{OA}|$:
$cos alpha=frac{a_{x}}{a}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить косинус угла, который образован вектором
$bar{a}=(-3 ; 4)$ и осью абсцисс.
Решение. Проекция на ось абсцисс равна
$a_x=-3$, длина вектора
$|bar{a}|=sqrt{(-3)^{2}+4^{2}}=5$, а тогда
$$cos alpha=frac{-3}{5}=-frac{3}{5}$$
Ответ. $cos alpha=-frac{3}{5}$
Читать дальше: что такое тангенс угла.
Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
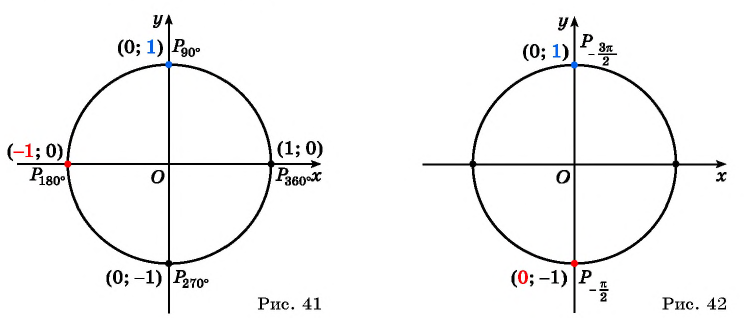
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Синус и косинус угла на единичной окружности
Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:
С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что
ВС = АВ•sinα = 5•0,8 = 4
Если известно, что cosα = 0,6, то мы сможем найти и второй катет:
АС = АВ•cosα = 5•0,6 = 3
Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:
tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)
Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты хА и уА:
Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:
Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле
Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда
АВ = sinα•ОА = sinα•1 = sinα
С другой стороны, видно, что величина отрезка АВ равна координате уА. Получается, что уА = АВ = sinα, или
Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:
Учитывая, что ОА = 1, а длина ОВ равна координате хА, мы получим следующее:
хА = ОВ = cosα•ОА = cosα•1 = cosα
то есть координата хА равна cos α:
Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.
Таким образом, нам удалось дать новое определение синусу и косинусу угла:
Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
http://100urokov.ru/predmety/urok-2-funkcii-trigonometricheskie




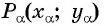
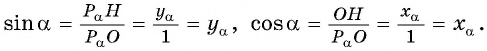
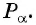
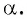
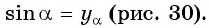
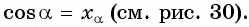
 единичной окружности.
единичной окружности.