Как найти косинус если синус с минусом

Ответ мой будет аналогичным ответу на похожий вопрос (см. здесь).

Из основного тригонометрического тождества:

выразим косинус в квадрате угла а:

Значит косинус угла равен либо корню квадратному из этого выражения, либо ему же, только со знаком -.

Знак перед корнем зависит от ограничения, которое накладывается для определенности в условии задачи.

Если дано положительное значение синуса,то угол находится в 1-й или во 2-й четверти. В первой четверти (0< a< 90) значение косинуса будет положительным. Здесь выбираем знак плюс. Во второй четверти (90< a< 180) значение косинуса будет отрицательным. Тогда перед корнем выбираем знак минус.

Если значение синуса отрицательное, то угол расположен в 3-й или 4-й четверти. В 3 четверти (180< a< 270) косинус угла будет меньше нуля.

В 4 четверти (270< a< 360) косинус угла будет больше нуля.

Примеры.

Пример 1. Найти косинус угла, если sina = -0,6. 180<a<270 (в градусах)

Решение. Находим разность 1 и квадрата значения sina, т.е. квадрата (-0,6).

-0,6 в квадрате находится так: (-0,6)*(-0,6) = 0,36. Подставим его в искомую разность:

1-0,36=0,64

Получили квадрат значения косинуса. Для нахождения значения самого косинуса, извлечем корень квадратный из 0,64 и возьмем его со знаком + или со знаком — . Получим 0,8 или -0,8.

Так как по условию угол находится в 3 четверти, то искомое значение косинуса будет также меньше нуля. Значит выбираем -0,8.

Ответ: cos a =-0,8.

Рассмотрим пример для случая, когда угол находится в 4 четверти:

Пример 2. Найти косинус угла, если sina = -0,6. 270<a<360 (в градусах)

Решение такое же (см. пример 1).

Перед выбором ответа рассуждаем так:

Т. к. по условию угол расположен в 4 четверти, то значение косинуса будет больше нуля. Значит выбираем 0,8.

Ответ: cos a =0,8.

Примеры: 

(sin⁡(-π)=-sin,⁡π)
(cos⁡(-225^° )=cos⁡, 225^°)
(tg(-frac{π}{2}-x)=-tg(frac{π}{2}+x))

И сразу два важных замечания.

Замечание №1

Многие ученики думают, что если можно вынести минус из тригонометрической функции, то можно вынести и число, но это не так:

(sin⁡,2x≠2 sin,⁡x)
(cos⁡,3x≠3cos,⁡x)
(tg,4x≠4tg,x)

Замечание №2

(sin^2⁡(-x)=sin^2⁡x)
(cos^2⁡(-x)=cos^2⁡x)
(tg^2 (-x)=tg^2 x)
(ctg^2 (-x)=ctg^2 x)

Квадрат меняет ситуацию. Всё дело в том, что (sin^2⁡(-x)=(sin⁡(-x) )^2=(-sin,⁡x )^2=sin^2⁡x), т.е. минус все равно выносится, но так как синуса два и они перемножаются, то в итоге получается плюс.

Примеры из ЕГЭ

Пример (ЕГЭ). Найдите значение выражения (24sqrt{2},cos⁡(-frac{π}{3}),sin⁡(-frac{π}{4})).
Решение. (24sqrt{2},cos⁡(-frac{π}{3}),sin⁡(-frac{π}{4})=-24sqrt{2},cos⁡frac{π}{3},sin⁡frac{π}{4}).

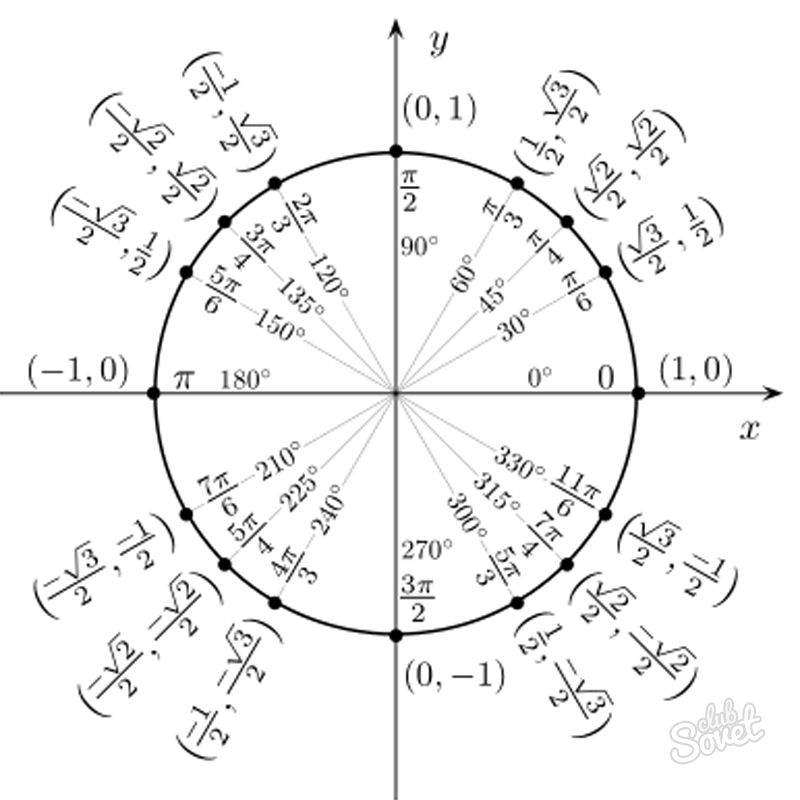
Из рисунка видно, что и косинус, и синус положителен. Косинус из трех стандартных значений (frac{1}{2}), (frac{sqrt{2}}{2}), (frac{sqrt{3}}{2}) принимает наименьшее т.е. (cos,⁡frac{π}{3}=frac{1}{2}). Синус из трех стандартных значений будет равен среднему т.е. (sin⁡,frac{π}{4}=frac{sqrt{2}}{2}). Получается:

(-24sqrt{2},cos⁡frac{π}{3},sin⁡frac{π}{4}=-24sqrt{2}cdot)(frac{1}{2})(cdot)(frac{sqrt{2}}{2})(=)(frac{-24sqrt{2}cdotsqrt{2}}{4})(=)(frac{-24cdot 2}{4})(=-6cdot2=-12)

Ответ: (-12).

Если вы не поняли почему (frac{π}{3}) и (frac{π}{4}) находятся на круге там, где мы из обозначили, то читайте статью «Как обозначать числа с пи на числовой окружности?». А если не поняли, как мы нашли синус и косинус, то читайте статью «Как найти синус и косинус без тригонометрической таблицы».

Пример (ЕГЭ). Найдите значение выражения (44sqrt{3},tg,(-480^° )).
Решение. (44sqrt{3},tg(-480^° )=-44sqrt{3},tg(480^° )=-44sqrt{3},tg(360^°+120^° )=-44sqrt{3},tg(360^°+90^°+30^°)).

Находим (480^°) на окружности:

Соединяем точку, соответствующую (480^°) и центр окружности, и продляем до оси тангенсов:

Мы попадаем в самое маленькое (из стандартных) значение тангенса.
Значит, (tg(480^° )=-sqrt{3}).
В итоге имеем: (44sqrt{3} tg(-480^° )=-44sqrt{3}cdot(-sqrt{3})=44cdot 3=132).
Ответ: (132).

Если вам не понятно, как мы нашли значение тангенса, то читайте статью «Как найти тангенс и котангенс без тригонометрической таблицы?».

Доказательства формул с минусом в аргументе:

Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.

Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).

Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.

Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника

Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co

Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.

Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.

Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.

Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.

Итак,

Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.

Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.

Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.

Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.

Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.

Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.

Как найти углы в прямоугольном треугольнике, если известны стороны?

Дан треугольник АВС, угол С — прямой.

Стороны АВ, АС и ВС известны.

Т.к. угол С — прямой, он равен 90 градусам.

Другие углы можно найти, например, так:

если известен катет и гипотенуза

sinA = BC / AB,

sinB = AC / AB,

если известны два катета

tg A = BC / AC

tg B = AC / BC

Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.

Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.

Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.

sin 15° = 0,259

arcsin0,259 = 15°

Как найти углы в прямоугольном треугольнике, если известен один угол?

Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.

Еединичная окружность (единичный круг)

Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).

Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).

Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.

Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).

Координатные четверти отсчитываются так:

                        y

                       |

                       |

(II четверть)   |   (I четверть)

                       |

________________________ x

                       |0

                       |

(III четверть)  |   (IV четверть)

                       |

                       |

Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).

Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).

Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).

Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).

Например:

• углы первой четверти: 30 градусов, 85 градусов, пи/4;
• углы второй четверти: 120 градусов, 178 градусов;
• углы третьей четверти: 205 градусов, 260 градусов;
• углы четвертой четверти: 272 градуса, 305 градусов.

Тригонометрические функции

К тригонометрическим функциям относятся функции:

y = sin x;

y = cos x;

y = tg x;

y = ctg x;

y = sec x;

y = cosec x.

Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.

Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.

Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.

Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.

Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.

Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.

Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.

Как найти синус угла, если известен косинус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

sin²a = 1 − cos²a

|sin a| = КОРЕНЬ(1 − cos²a)

sin a = ± КОРЕНЬ(1 − cos²a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)

Как найти косинус угла, если известен синус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

cos²a = 1 − sin²a

|cos a| = КОРЕНЬ(1 − sin²a)

cos a = ± КОРЕНЬ(1 − sin²a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)

Как найти синус угла, если известен котангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + ctg² a = 1/sin² a

sin² a = 1 / (1 + ctg² a)

|sin a| = 1/ КОРЕНЬ(1 + ctg² a)

sin a = ±1/ КОРЕНЬ(1 + ctg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)

Как найти косинус угла, если известен тангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + tg² a = 1/cos² a

cos² a = 1 / (1 + tg² a)

|cos a| = 1/ КОРЕНЬ(1 + tg² a)

cos a = ±1/ КОРЕНЬ(1 + tg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)

Тригонометрическое тождество

Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.

Основные тригонометрические тождества:

sin²a + cos²a = 1

tg a = sin a / cos a

ctg a = cos a / sin a

sec a = 1 / cos a

cosec a = 1 / sin a

Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)

• arcsin — читается: арксинус;
• arcos — читается: арккосинус;
• arctg — читается: арктангенс;
• arcctg — читается: арккотангенс.

arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.

Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:

y = arcsin x sin y = x

Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:

y = arccos x cos y = x

Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:

y = arctg x tg y = x

Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:

y = arctg x tg y = x

Например,

sin 30° = 0,5

arcsin0,5 = 30°

Синусоида и косинусоида

График функции y = sin x называется синусоидой.

График функции y = cos x называется косинусоидой.

Источники информации:

• Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
• В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
• docme.ru — зачем нужна тригонометрия?
• ru.wikipedia.org — Википедия — тригонометрия;
• ru.wikihow.com — как изучать тригонометрию?

Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.

Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.

В математике применяются основные определения, связанные с тригонометрией. А именно:

• синус — соотношение стороны противолежащего катета к стороне гипотенузы, (sin);
• косинус — это прилежащая сторона катет к гипотенузе, обозначается как (cos);

Стоит выделить главные тригонометрические тождества, существующие в математике:

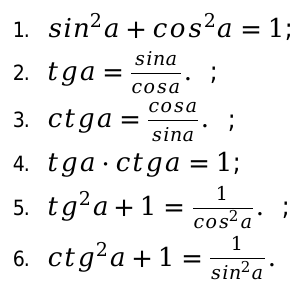
Применим основные формулы тригонометрии, решая задачи.

Пример:

Известно: [cos alpha=0.8];

Необходимо определить: косинус, тангенс, котангенс, соответствующего угла a.

Решение:

Для определения значения косинуса в квадрате, возводим число 0,8 в квадрат и вычисляем синус. Полученное значение подставляем в формулу и можем определить тангенс угла 0,8. Таким же методом, вычисляем котангенс

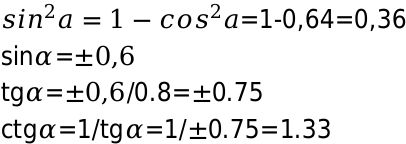
Решение довольно простое и особых сложней не вызывает.

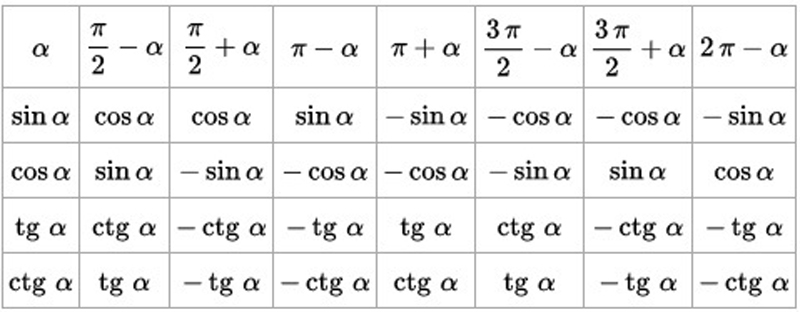
Основные формулы для приведения заданных значений:

Формулы помогают, преобразовать основные тождества и перейти к вычислению углов в пределах 90 градусов. Это очень удобно, не только в алгебре, но и во всей математике.

Существует два основных способа, использования формул приведения:

• Если угол можно записать как [(pi / 2 pm alpha)] или [left(3^{*} pi / 2 pm alpharight)], то название функции меняется с  косинуса на определение синус, тангенс, в свою очередь на котангенс, либо наоборот. Если же угол можно представить в виде [(pi pm alpha)] или [(2 * pi pm alpha)], то название функции не меняется.

• Обозначение приведенного уравнения не изменяется. Если изначально функция была со знаком «+», тогда и приведенная функция будет со знаком «+», с отрицательным знаком тоже самое.

Используя основные определения математики, а именно тригонометрии. Можно определить нужные нам данные.

Значения функций тригонометрии на для основных угловых значений.

• синуса (sin):

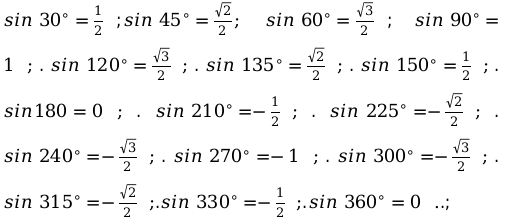
• косинуса (cos):

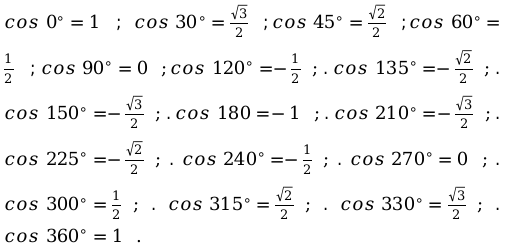
Преобразовав формулы сложения, мы получим тригонометрические уравнения угла.

Формулы кратности значения угла:

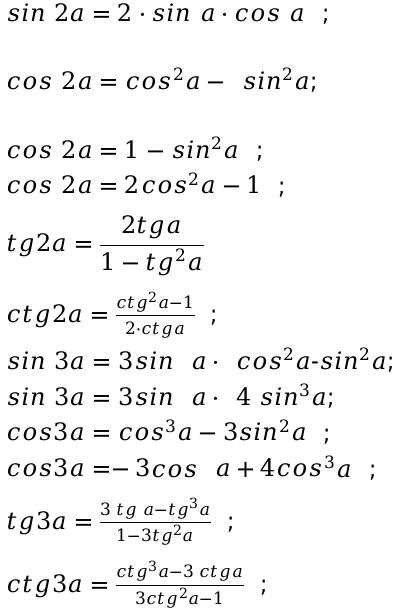
Формулы угла, определяющие половину значения (половинного угла):

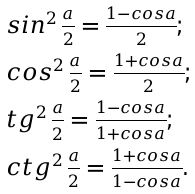
Более подробно в данном материале мы рассмотрим все уравнения суммы и разности, связанные именно с функцией косинус и синус.

Основные формулы для определения суммы и разности cos и sin

Перейдем к рассмотрению к простой форме разности и суммы функций.

Рассматриваемое уравнений можно представить, как — произведение. Преобразовать на множители косинус или синус, и тем самым упростить процесс вычисления.

Составим и запишем основные формулы для функции синус.

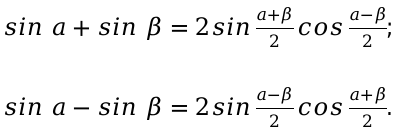
Следующим основным  шагом, будет составить уравнения для косинуса. Применим все изученные свойства данной функции тригонометрии и вычислим правильный ответ.

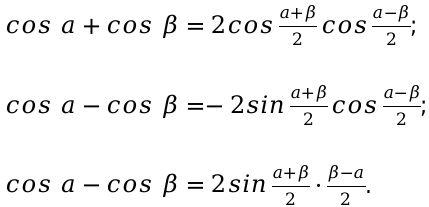
Выведем основные формулы для решения функций двух угловых значений. Для этого нужно применить составленные выше формулы сложения и вычитания. Их рассмотрение было в предыдущих материалах, посвященных тригонометрии. Поэтому лишний раз не стоит их заново переписывать. Так как рекомендовалась их обязательно заучить наизусть. Для более быстрого и правильного решения уравнений. И для последующего использования при изучении других смежных тем, где эти функции применяются.

Формулы можно представить также в виде полусуммы и полуразности угловых значений и получить следующие формулы.

Запишем уравнение для каждого угла раздельно и получим следующие  формулы в виде уравнения:

[ alpha=frac{a+beta}{2}+frac{a-beta}{2}=frac{a}{2}+frac{beta}{2}+frac{a}{2}-frac{beta}{2} ]

[ beta=frac{a+beta}{2}-frac{a-beta}{2}=frac{a}{2}+frac{beta}{2}-frac{a}{2}+frac{beta}{2} ]

Сравним записанные формулы для угловых значений. Проанализировав их становится очевидно, что полученные суммы функций одинаковы по значению.

Выведем основную формулу для решения:

[ sin a+sin beta=sin left(frac{a+beta}{2}+frac{a-beta}{2}right)+sin left(frac{a+beta}{2}-frac{a-beta}{2}right) . ]

Далее первую часть выражения преобразуем, для этого применим формулу для сложения функций. Значения, которые находятся после знака равно, преобразуются при помощи формулы синуса для разности.

Подставляя в формулу значения, получаем следующее выражение:

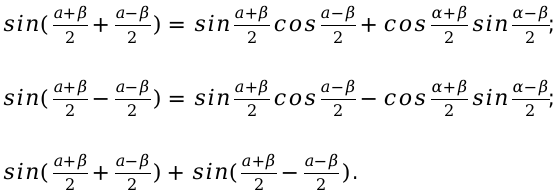
Далее необходимо раскрыть скобки и полученные значения привести в подобные слагаемые.  Произведя все действия мы в конечном итоге получаем нужную нам формулу.

Запишем формулу следующего вида:

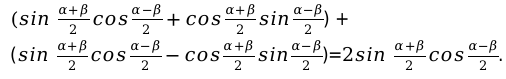
Другие, формулы преобразуются аналогичным способом

Итоговые формулы сложения и вычитания тригонометрических функций

Формула определения разности для синуса:

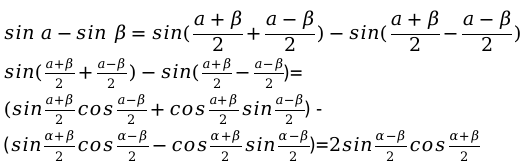
Формула для расчета суммы косинуса:

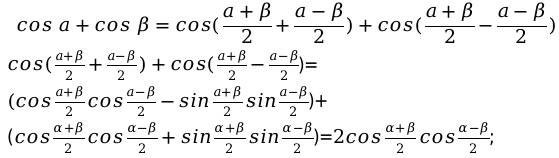
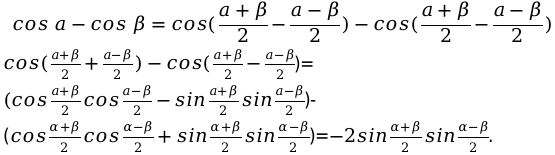
Рассмотрим на практике применение изученного материала. Для этого решим несколько задач, подставляя числовые угловые значения

Пример №1:

По заданию нужно проверить сумму угловых значений для изученной функции подставив данные в формулу.

Заданы значения: [alpha=frac{pi}{2} ; beta=frac{pi}{6}].

Подберем нужную формулу и произведем вычисление:

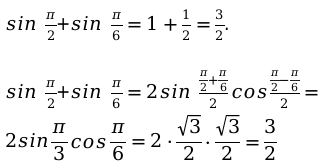
Пример №2:

В этом примере рассмотрим вариант решения и применения формулы, для разности функции синуса.

Заданы следующие значения.

Углы: [alpha=165^{circ}, beta=75^{circ}]

Подставим угловые значения в формулу:

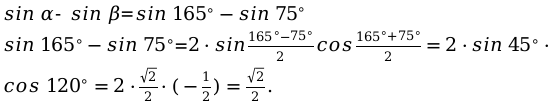
Пример №3:

Нужно найти сумму тригонометрической функции.

Для этого заданы угловые значения.

Применяя основные изученные формулы, решим данную задачу.

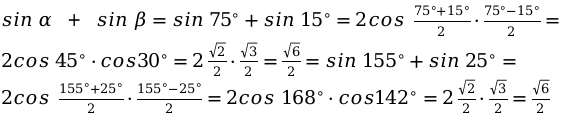
Применяя вышеизложенные формулы можно перейти к произведению функций.

В целом, данная тема, считается основой в алгебре. Однако стоит вспомнить, что данные функции имеют главную роль и в других технических науках.

Они встречаются во многих теоремах, особенно это свойственно для физики.

Для всех технических наук, характерна взаимосвязь между основными законами и теоремами. Поэтому для успешного решения задач разного уровня, необходимо изучать и уметь их всех применять на практике.