Рассмотрим
множество функций
,
,
(4.5.1)
определенных
на отрезке
и имеющих множества значений, принадлежащих
отрезку.
По формуле (4.5.1) непосредственно получим:
,
.
(4.5.2)
Покажем,
что
совпадает с алгебраическим многочленомn-й
степени при любом натуральном значении
n.
Обозначим
.
Тогда
.
(4.5.3)
По
известной тригонометрической формуле
.
Учитывая
равенство (4.5.3), последнюю формулу можно
записать в виде
.
Выразим
из последней формулы
и, учитывая равенства (4.5.2), получим
рекуррентную формулу
.
(4.5.4)
Вычисляя
по этой рекуррентной формуле функции
последовательно при
получим
,
,
,
,
…
Легко
видеть, что, продолжая эти вычисления,
мы на каждом шаге будем получать
алгебраические многочлены, причем
степени их каждый раз будет увеличиваться
на 1. Таким образом, функция
совпадает в области определения с
алгебраическим многочленомn-й
степени при любом натуральном значении
n.
Функции
получили названиемногочленов
Чебышева.
Рассмотрим некоторые свойства многочленов
Чебышева.
Найдем
корни многочленов Чебышева. Для этого
решим уравнение
при
.
Из него непосредственно получим
.
(4.5.5)
Здесь
величина k
может принимать любые целые значения.
Но уравнение (4.5.5) будет иметь решения
относительно x
только при тех значениях k,
при которых значение величины

.
Поэтому уравнение (4.5.5) будет иметь
решения относительноx
только при тех значениях k,
при которых
.
(4.5.6)
Условия
(4.5.6) будут выполняться при
(
).
Например, привеличинаk
может принять только одно значение
.
При
.
При
и так далее. Зафиксируем некоторое
натуральное значениеn.
Для каждого из значений
уравнение (4.5.5) будет иметь единственное
решение:
,
.
(4.5.7)
Таким
образом, функция
(
)
будет иметьn
корней на отрезке
и все эти корни получаются по формулам
(4.5.7).
Найдем
коэффициенты при старшей степени
многочленов Чебышева. Рассматривая
формулы для
при
легко заметить, что при
единственный коэффициент многочлена
равен 1, а при
коэффициенты при старшей степени
многочленовравны
.
Методом математической индукции с
помощью формулы (4.5.4) легко доказать,
что коэффициенты при старшей степени
многочленовравны
при любых натуральных значенияхn.
Наряду
с введенными многочленами Чебышева,
часто используются и нормированные
многочлены Чебышева, получаемые из
путем деления их на коэффициенты при
старшей степени:
,
=
,
(4.5.8)
многочлены
с коэффициентами при старшей степени,
равными 1.
Функции
(
),
так же как и,
будут иметьn
корней на отрезке
,
и все эти корни получаются по формулам
(4.5.7). Кроме того, они обладают одним
замечательным свойством, которое мы
приведем без доказательства.
Теорема 1 (теорема
Чебышева).
Из всех многочленов степени n+1
с коэффициентами при старшей степени,
равными 1 (многочленов вида
),
нормированный многочлен Чебышеванаименее уклоняется от нуля на отрезке
.
То естьпринимает наименьшее значение, если
.
Наименьшее значениеравно 1 при
,
а при всех остальных натуральных
значенияхn
наименьшее значение
будет равно
.
Чебышевские узлы
интерполяции
В
параграфе 4.1 была доказана оценка
погрешности многочленной интерполяции.
Если интерполируемая функция
имеет на отрезке
ограниченную производнуюn+1-го
порядка и существует положительная
постоянная
такая, что
на отрезке
для любогоx,
принадлежащего отрезку
будет справедлива оценка погрешности
интерполяционного многочлена(4.1.15)
.
В
этой оценке только величина
зависит отx.
Величина
неотрицательна. Поэтому наименьшее
значение погрешность интерполяции на
отрезке
,
при которых принимает наименьшее
значение величина.
Вычислим эти значения. Введем для этого
линейное преобразование
,
(4.5.9)
которое
отображает отрезок
на отрезок
.
Обратное преобразование, отображающеена
,
очевидно, имеет вид
.
(4.5.10)
Введем
точки
,
(4.5.11)
соответствующие
точкам
.
Поскольку точки,
соответствующие им точки.
Зная точки,
можно получить соответствующие точкипо формуле
,
.
(4.5.12)
Сделаем
в выражении
замену переменных по формулам (4.5.9),
(4.5.12):

(4.5.13)
Согласно
теореме Чебышева,
достигается, если
совпадают с корнями многочленов Чебышева
:
,
.
(4.5.14)
Чтобы
получить эту формулу, необходимо в
формуле (4.5.7) заменить x
на t,
а n
на n+1.
Причем этот минимум равен
.Таким
образом, если
выбрать узлы интерполяции
на
отрезке
по
формулам
(4.5.14), (4.5.12),
то оценка
погрешности интерполяции

наименьшее значение, равное
.
Эти узлы получили названиечебышевских
узлов интерполяции.
Если
выбраны чебышевские узлы интерполяции
,
то будет справедлива оценка погрешности
интерполяции
:
.
(4.5.15)
Эту
оценку называют наилучшей
равномерной оценкой погрешности
интерполяции.
Ее можно использовать для того, чтобы
ответить на вопрос об условиях сходимости
интерполяционных многочленов Лагранжак
при
.
Пусть функцияимеет производные любого порядка на
отрезкеи существует постояннаяМ
такая, что для
:
(здесь
мажорантные оценки модуля производной
на отрезке
).
Тогда

А
поскольку длявыполняется неравенство
,
то
согласно теореме о промежуточной
последовательности,
.
Таким
образом, если функция
имеет производные любого порядка на
отрезкеи существует постояннаяМ
такая, что
:
,
а для интерполяции на отрезкевыбираются чебышевские узлы, то
погрешность интерполяции будет стремиться
к 0 при.
Соседние файлы в папке ВМ_УЧЕБНИК
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Plot of the Chebyshev polynomial of the first kind T n(x) with n=5 in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
The Chebyshev polynomials are two sequences of polynomials related to the cosine and sine functions, notated as 

The Chebyshev polynomials of the first kind 
Similarly, the Chebyshev polynomials of the second kind 
That these expressions define polynomials in 











An important and convenient property of the Tn(x) is that they are orthogonal with respect to the inner product:
and Un(x) are orthogonal with respect to another, analogous inner product, given below.
The Chebyshev polynomials Tn are polynomials with the largest possible leading coefficient whose absolute value on the interval [−1, 1] is bounded by 1. They are also the «extremal» polynomials for many other properties.[1]
Chebyshev polynomials are important in approximation theory because the roots of Tn(x), which are also called Chebyshev nodes, are used as matching points for optimizing polynomial interpolation. The resulting interpolation polynomial minimizes the problem of Runge’s phenomenon and provides an approximation that is close to the best polynomial approximation to a continuous function under the maximum norm, also called the «minimax» criterion. This approximation leads directly to the method of Clenshaw–Curtis quadrature.
These polynomials were named after Pafnuty Chebyshev.[2] The letter T is used because of the alternative transliterations of the name Chebyshev as Tchebycheff, Tchebyshev (French) or Tschebyschow (German).
Definitions[edit]
Recurrence definition[edit]
Plot of the first five Tn Chebyshev polynomials (first kind)
The Chebyshev polynomials of the first kind are obtained from the recurrence relation
The recurrence also allows to represent them explicitly as the determinant of a tridiagonal matrix of size 
The ordinary generating function for Tn is
There are several other generating functions for the Chebyshev polynomials; the exponential generating function is
The generating function relevant for 2-dimensional potential theory and multipole expansion is
Plot of the first five Un Chebyshev polynomials (second kind)
The Chebyshev polynomials of the second kind are defined by the recurrence relation
Notice that the two sets of recurrence relations are identical, except for 

The ordinary generating function for Un is
and the exponential generating function is
Trigonometric definition[edit]
As described in the introduction, the Chebyshev polynomials of the first kind can be defined as the unique polynomials satisfying
or, in other words, as the unique polynomials satisfying
for n = 0, 1, 2, 3, … which as a technical point is a variant (equivalent transpose) of Schröder’s equation. That is, Tn(x) is functionally conjugate to n x, codified in the nesting property below.
The polynomials of the second kind satisfy:
or
which is structurally quite similar to the Dirichlet kernel Dn(x):
(The Dirichlet kernel, in fact, coincides with what is now known as the Chebyshev polynomial of the fourth kind.)
That cos nx is an nth-degree polynomial in cos x can be seen by observing that cos nx is the real part of one side of de Moivre’s formula. The real part of the other side is a polynomial in cos x and sin x, in which all powers of sin x are even and thus replaceable through the identity cos2 x + sin2 x = 1.
By the same reasoning, sin nx is the imaginary part of the polynomial, in which all powers of sin x are odd and thus, if one factor of sin x is factored out, the remaining factors can be replaced to create a (n−1)st-degree polynomial in cos x.
The identity is quite useful in conjunction with the recursive generating formula, inasmuch as it enables one to calculate the cosine of any integer multiple of an angle solely in terms of the cosine of the base angle.
Chebyshev polynomials of the first kind can be computed directly from the Euler’s identity
Expanding the latter, one gets
Then, to get the expression for 


which in turn means that
Alternatively, the first two Chebyshev polynomials of the first kind are computed directly from the definition to be
and
while the rest may be evaluated using a specialization of the product-to-sum identity
as, for example,
Conversely, an arbitrary integer power of trigonometric functions may be expressed as a linear combination of trigonometric functions using Chebyshev polynomials
where the prime at the summation symbol indicates that the contribution of j = 0 needs to be halved if it appears, and 
An immediate corollary is the expression of complex exponentiation in terms of Chebyshev polynomials: given z = a + bi,
Commuting polynomials definition[edit]
Chebyshev polynomials can also be characterized by the following theorem:[3]
If 









Pell equation definition[edit]
The Chebyshev polynomials can also be defined as the solutions to the Pell equation
in a ring R[x].[4] Thus, they can be generated by the standard technique for Pell equations of taking powers of a fundamental solution:
Relations between the two kinds of Chebyshev polynomials[edit]
The Chebyshev polynomials of the first and second kinds correspond to a complementary pair of Lucas sequences Ṽn(P, Q) and Ũn(P, Q) with parameters P = 2x and Q = 1:
It follows that they also satisfy a pair of mutual recurrence equations:[5]
The second of these may be rearranged using the recurrence definition for the Chebyshev polynomials of the second kind to give
Using this formula iteratively gives the sum formula
while replacing 



This relationship is used in the Chebyshev spectral method of solving differential equations.
Turán’s inequalities for the Chebyshev polynomials are[6]
The integral relations are[5]: 187(47)(48) [7]
where integrals are considered as principal value.
Explicit expressions[edit]
Different approaches to defining Chebyshev polynomials lead to different explicit expressions such as:
with inverse[8][9]
where the prime at the summation symbol indicates that the contribution of j = 0 needs to be halved if it appears.
where 2F1 is a hypergeometric function.
Properties[edit]
Symmetry[edit]
That is, Chebyshev polynomials of even order have even symmetry and therefore contain only even powers of x. Chebyshev polynomials of odd order have odd symmetry and therefore contain only odd powers of x.
Roots and extrema[edit]
A Chebyshev polynomial of either kind with degree n has n different simple roots, called Chebyshev roots, in the interval [−1, 1]. The roots of the Chebyshev polynomial of the first kind are sometimes called Chebyshev nodes because they are used as nodes in polynomial interpolation. Using the trigonometric definition and the fact that
one can show that the roots of Tn are
Similarly, the roots of Un are
The extrema of Tn on the interval −1 ≤ x ≤ 1 are located at
One unique property of the Chebyshev polynomials of the first kind is that on the interval −1 ≤ x ≤ 1 all of the extrema have values that are either −1 or 1. Thus these polynomials have only two finite critical values, the defining property of Shabat polynomials. Both the first and second kinds of Chebyshev polynomial have extrema at the endpoints, given by:
The extrema of 












Specifically,[10][11] when 
When 
This result has been generalized to solutions of 


Differentiation and integration[edit]
The derivatives of the polynomials can be less than straightforward. By differentiating the polynomials in their trigonometric forms, it can be shown that:
The last two formulas can be numerically troublesome due to the division by zero (0/0 indeterminate form, specifically) at x = 1 and x = −1. It can be shown that:
Proof
The second derivative of the Chebyshev polynomial of the first kind is
which, if evaluated as shown above, poses a problem because it is indeterminate at x = ±1. Since the function is a polynomial, (all of) the derivatives must exist for all real numbers, so the taking to limit on the expression above should yield the desired values – taking the limit as x → 1:
Factoring the denominator:
Since the limit as a whole must exist, the limit of the numerator and denominator must independently exist, and
The denominator (still) limits to zero, which implies that the numerator must be limiting to zero, i.e. Un − 1(1) = nTn(1) = n which will be useful later on. Since the numerator and denominator are both limiting to zero, L’Hôpital’s rule applies:
The proof for x = −1 is similar, with the fact that Tn(−1) = (−1)n being important.
More general formula states:
which is of great use in the numerical solution of eigenvalue problems.
Also, we have
where the prime at the summation symbols means that the term contributed by k = 0 is to be halved, if it appears.
Concerning integration, the first derivative of the Tn implies that
and the recurrence relation for the first kind polynomials involving derivatives establishes that for n ≥ 2
The last formula can be further manipulated to express the integral of Tn as a function of Chebyshev polynomials of the first kind only:
Furthermore, we have
Products of Chebyshev polynomials[edit]
The Chebyshev polynomials of the first kind satisfy the relation
which is easily proved from the product-to-sum formula for the cosine,
For n = 1 this results in the already known recurrence formula, just arranged differently, and with n = 2 it forms the recurrence relation for all even or all odd indexed Chebyshev polynomials (depending on the parity of the lowest m) which implies the evenness or oddness of these polynomials. Three more useful formulas for evaluating Chebyshev polynomials can be concluded from this product expansion:
The polynomials of the second kind satisfy the similar relation
(with the definition U−1 ≡ 0 by convention ).
They also satisfy
for m ≥ n.
For n = 2 this recurrence reduces to
which establishes the evenness or oddness of the even or odd indexed Chebyshev polynomials of the second kind depending on whether m starts with 2 or 3.
Composition and divisibility properties[edit]
The trigonometric definitions of Tn and Un imply the composition or nesting properties[13]
For Tmn the order of composition may be reversed, making the family of polynomial functions Tn a commutative semigroup under composition.
Since Tm(x) is divisible by x if m is odd, it follows that Tmn(x) is divisible by Tn(x) if m is odd. Furthermore, Umn−1(x) is divisible by Un−1(x), and in the case that m is even, divisible by Tn(x)Un−1(x).
Orthogonality[edit]
Both Tn and Un form a sequence of orthogonal polynomials. The polynomials of the first kind Tn are orthogonal with respect to the weight
on the interval [−1, 1], i.e. we have:
This can be proven by letting x = cos θ and using the defining identity Tn(cos θ) = cos(nθ).
Similarly, the polynomials of the second kind Un are orthogonal with respect to the weight
on the interval [−1, 1], i.e. we have:
(The measure √1 − x2 dx is, to within a normalizing constant, the Wigner semicircle distribution.)
These orthogonality properties follow from the fact that the Chebyshev polynomials solve the Chebyshev differential equations
which are Sturm–Liouville differential equations. It is a general feature of such differential equations that there is a distinguished orthonormal set of solutions. (Another way to define the Chebyshev polynomials is as the solutions to those equations.)
The Tn also satisfy a discrete orthogonality condition:
where N is any integer greater than max(i, j),[7] and the xk are the N Chebyshev nodes (see above) of TN (x):
For the polynomials of the second kind and any integer N > i + j with the same Chebyshev nodes xk, there are similar sums:
and without the weight function:
For any integer N > i + j, based on the N zeros of UN (x):
one can get the sum:
and again without the weight function:
Minimal ∞-norm[edit]
For any given n ≥ 1, among the polynomials of degree n with leading coefficient 1 (monic polynomials),
is the one of which the maximal absolute value on the interval [−1, 1] is minimal.
This maximal absolute value is
and |f(x)| reaches this maximum exactly n + 1 times at
Proof
Let’s assume that wn(x) is a polynomial of degree n with leading coefficient 1 with maximal absolute value on the interval [−1, 1] less than 1 / 2n − 1.
Define
Because at extreme points of Tn we have
From the intermediate value theorem, fn(x) has at least n roots. However, this is impossible, as fn(x) is a polynomial of degree n − 1, so the fundamental theorem of algebra implies it has at most n − 1 roots.
[edit]
By the equioscillation theorem, among all the polynomials of degree ≤ n, the polynomial f minimizes ‖ f ‖∞ on [−1, 1] if and only if there are n + 2 points −1 ≤ x0 < x1 < ⋯ < xn + 1 ≤ 1 such that | f(xi)| = ‖ f ‖∞.
Of course, the null polynomial on the interval [−1, 1] can be approximated by itself and minimizes the ∞-norm.
Above, however, | f | reaches its maximum only n + 1 times because we are searching for the best polynomial of degree n ≥ 1 (therefore the theorem evoked previously cannot be used).
Chebyshev polynomials as special cases of more general polynomial families[edit]
The Chebyshev polynomials are a special case of the ultraspherical or Gegenbauer polynomials 

Chebyshev polynomials are also a special case of Dickson polynomials:
In particular, when 


Other properties[edit]
The curves given by y = Tn(x), or equivalently, by the parametric equations y = Tn(cos θ) = cos nθ, x = cos θ, are a special case of Lissajous curves with frequency ratio equal to n.
Similar to the formula
we have the analogous formula
For x ≠ 0,
and
which follows from the fact that this holds by definition for x = eiθ.
Examples[edit]
First kind[edit]
The first few Chebyshev polynomials of the first kind in the domain −1 < x < 1: The flat T0, T1, T2, T3, T4 and T5.
The first few Chebyshev polynomials of the first kind are OEIS: A028297
Second kind[edit]
The first few Chebyshev polynomials of the second kind in the domain −1 < x < 1: The flat U0, U1, U2, U3, U4 and U5. Although not visible in the image, Un(1) = n + 1 and Un(−1) = (n + 1)(−1)n.
The first few Chebyshev polynomials of the second kind are OEIS: A053117
As a basis set[edit]
The non-smooth function (top) y = −x3H(−x), where H is the Heaviside step function, and (bottom) the 5th partial sum of its Chebyshev expansion. The 7th sum is indistinguishable from the original function at the resolution of the graph.
In the appropriate Sobolev space, the set of Chebyshev polynomials form an orthonormal basis, so that a function in the same space can, on −1 ≤ x ≤ 1, be expressed via the expansion:[14]
Furthermore, as mentioned previously, the Chebyshev polynomials form an orthogonal basis which (among other things) implies that the coefficients an can be determined easily through the application of an inner product. This sum is called a Chebyshev series or a Chebyshev expansion.
Since a Chebyshev series is related to a Fourier cosine series through a change of variables, all of the theorems, identities, etc. that apply to Fourier series have a Chebyshev counterpart.[14] These attributes include:
- The Chebyshev polynomials form a complete orthogonal system.
- The Chebyshev series converges to f(x) if the function is piecewise smooth and continuous. The smoothness requirement can be relaxed in most cases – as long as there are a finite number of discontinuities in f(x) and its derivatives.
- At a discontinuity, the series will converge to the average of the right and left limits.
The abundance of the theorems and identities inherited from Fourier series make the Chebyshev polynomials important tools in numeric analysis; for example they are the most popular general purpose basis functions used in the spectral method,[14] often in favor of trigonometric series due to generally faster convergence for continuous functions (Gibbs’ phenomenon is still a problem).
Example 1[edit]
Consider the Chebyshev expansion of log(1 + x). One can express
One can find the coefficients an either through the application of an inner product or by the discrete orthogonality condition. For the inner product,
which gives
Alternatively, when the inner product of the function being approximated cannot be evaluated, the discrete orthogonality condition gives an often useful result for approximate coefficients,
where δij is the Kronecker delta function and the xk are the N Gauss–Chebyshev zeros of TN (x):
For any N, these approximate coefficients provide an exact approximation to the function at xk with a controlled error between those points. The exact coefficients are obtained with N = ∞, thus representing the function exactly at all points in [−1,1]. The rate of convergence depends on the function and its smoothness.
This allows us to compute the approximate coefficients an very efficiently through the discrete cosine transform
Example 2[edit]
To provide another example:
Partial sums[edit]
The partial sums of
are very useful in the approximation of various functions and in the solution of differential equations (see spectral method). Two common methods for determining the coefficients an are through the use of the inner product as in Galerkin’s method and through the use of collocation which is related to interpolation.
As an interpolant, the N coefficients of the (N − 1)st partial sum are usually obtained on the Chebyshev–Gauss–Lobatto[15] points (or Lobatto grid), which results in minimum error and avoids Runge’s phenomenon associated with a uniform grid. This collection of points corresponds to the extrema of the highest order polynomial in the sum, plus the endpoints and is given by:
Polynomial in Chebyshev form[edit]
An arbitrary polynomial of degree N can be written in terms of the Chebyshev polynomials of the first kind.[7] Such a polynomial p(x) is of the form
Polynomials in Chebyshev form can be evaluated using the Clenshaw algorithm.
[edit]
Polynomials denoted 

and satisfy
A. F. Horadam called the polynomials 




Shifted Chebyshev polynomials of the first and second kinds are related to the Chebyshev polynomials by[16]
When the argument of the Chebyshev polynomial satisfies 2x − 1 ∈ [−1, 1] the argument of the shifted Chebyshev polynomial satisfies x ∈ [0, 1]. Similarly, one can define shifted polynomials for generic intervals [a, b].
Around 1990 the terms «third-kind» and «fourth-kind» came into use in connection with Chebyshev polynomials, although the polynomials denoted by these terms had an earlier development under the name airfoil polynomials. According to J. C. Mason and G. H. Elliott, the terminology «third-kind» and «fourth-kind» is due to Walter Gautschi, «in consultation with colleagues in the field of orthogonal polynomials.»[19] The Chebyshev polynomials of the third kind are defined as
and the Chebyshev polynomials of the fourth kind are defined as
where 








and are proportional to Jacobi polynomials 
[20]
All four families satisfy the recurrence 










See also[edit]
- Chebyshev filter
- Chebyshev cube root
- Dickson polynomials
- Legendre polynomials
- Hermite polynomials
- Minimal polynomial of 2cos(2pi/n)
- Romanovski polynomials
- Chebyshev rational functions
- Approximation theory
- The Chebfun system
- Discrete Chebyshev transform
- Markov brothers’ inequality
- Clenshaw algorithm
References[edit]
- ^ Rivlin, Theodore J. (1974). «Chapter 2, Extremal properties». The Chebyshev Polynomials. Pure and Applied Mathematics (1st ed.). New York-London-Sydney: Wiley-Interscience [John Wiley & Sons]. pp. 56–123. ISBN 978-047172470-4.
- ^ Chebyshev polynomials were first presented in Chebyshev, P. L. (1854). «Théorie des mécanismes connus sous le nom de parallélogrammes». Mémoires des Savants étrangers présentés à l’Académie de Saint-Pétersbourg (in French). 7: 539–586.
- ^ Ritt, J. F. (1922). «Prime and Composite Polynomials». Trans. Amer. Math. Soc.: 51–66. doi:10.1090/S0002-9947-1922-1501189-9.
- ^ Demeyer, Jeroen (2007). Diophantine Sets over Polynomial Rings and Hilbert’s Tenth Problem for Function Fields (PDF) (Ph.D. thesis). p. 70. Archived from the original (PDF) on 2 July 2007.
- ^ a b Erdélyi, Arthur; Magnus, (Hans Heinrich) Wilhelm; Oberhettinger, Fritz [in German]; Tricomi, Francesco Giacomo; Bertin, David; Fulks, Watson B.; Harvey, Albert Raymond; Thomsen, Jr., Donald L.; Weber, Maria A.; Whitney, Eoin Laird [at Wikidata]; Stampfel, Rosemarie (1953). Erdélyi, Arthur (ed.). Higher Transcendental Functions — Volume II — Based, in part, on notes left by Harry Bateman (PDF). Bateman Manuscript Project. Vol. II (1 ed.). New York / Toronto / London: McGraw-Hill Book Company, Inc. p. 184:(3),(4). LCCN 53-5555. Contract No. N6onr-244 Task Order XIV. Project Designation Number: NR 043-045. Order No. 19546. Archived (PDF) from the original on 9 April 2017. Retrieved 23 July 2020. [1][2] (xvii+1 errata page+396 pages, red cloth hardcover) (NB. Copyright was renewed by California Institute of Technology in 1981.); Reprint: Robert E. Krieger Publishing Co., Inc., Melbourne, Florida, USA. 1981. ISBN 0-89874-069-X; Planned Dover reprint: ISBN 0-486-44615-8.
- ^ Beckenbach, E. F.; Seidel, W.; Szász, Otto (1951), «Recurrent determinants of Legendre and of ultraspherical polynomials», Duke Math. J., 18: 1–10, doi:10.1215/S0012-7094-51-01801-7, MR 0040487
- ^ a b c Mason & Handscomb 2002.
- ^ Cody, W. J. (1970). «A survey of practical rational and polynomial approximation of functions». SIAM Review. 12 (3): 400–423. doi:10.1137/1012082.
- ^ Mathar, R. J. (2006). «Chebyshev series expansion of inverse polynomials». J. Comput. Appl. Math. 196 (2): 596–607. arXiv:math/0403344. Bibcode:2006JCoAM..196.596M. doi:10.1016/j.cam.2005.10.013. S2CID 16476052.
- ^ Gürtaş, Y. Z. (2017). «Chebyshev Polynomials and the minimal polynomial of
«. American Mathematical Monthly. 124 (1): 74—78. doi:10.4169/amer.math.monthly.124.1.74.
- ^ a b Wolfram, D. A. (2022). «Factoring Chebyshev polynomials of the first and second kinds with minimal polynomials of
«. American Mathematical Monthly. 129 (2): 172—176. doi:10.1080/00029890.2022.2005391.
- ^ Wolfram, D. A. (2022). «Factoring Chebyshev polynomials with minimal polynomials of
«. Bulletin of the Australian Mathematical Society. arXiv:2106.14585. doi:10.1017/S0004972722000235.
- ^ Rayes, M. O.; Trevisan, V.; Wang, P. S. (2005), «Factorization properties of chebyshev polynomials», Computers & Mathematics with Applications, 50 (8–9): 1231–1240, doi:10.1016/j.camwa.2005.07.003
- ^ a b c Boyd, John P. (2001). Chebyshev and Fourier Spectral Methods (PDF) (second ed.). Dover. ISBN 0-486-41183-4. Archived from the original (PDF) on 31 March 2010. Retrieved 19 March 2009.
- ^ «Chebyshev Interpolation: An Interactive Tour». Archived from the original on 18 March 2017. Retrieved 2 June 2016.
- ^ a b Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 22». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 778. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- ^ Horadam, A. F. (2002), «Vieta polynomials» (PDF), Fibonacci Quarterly, 40 (3): 223–232
- ^ Viète, François (1646). Francisci Vietae Opera mathematica : in unum volumen congesta ac recognita / opera atque studio Francisci a Schooten (PDF). Bibliothèque nationale de France.
- ^ a b c Mason, J. C.; Elliott, G. H. (1993), «Near-minimax complex approximation by four kinds of Chebyshev polynomial expansion», J. Comput. Appl. Math., 46: 291–300, doi:10.1016/0377-0427(93)90303-S
- ^ a b Desmarais, Robert N.; Bland, Samuel R. (1995), «Tables of properties of airfoil polynomials», NASA Reference Publication 1343, National Aeronautics and Space Administration
Sources[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 22». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Dette, Holger (1995). «A note on some peculiar nonlinear extremal phenomena of the Chebyshev polynomials». Proceedings of the Edinburgh Mathematical Society. 38 (2): 343–355. arXiv:math/9406222. doi:10.1017/S001309150001912X. S2CID 16703489.
- Elliott, David (1964). «The evaluation and estimation of the coefficients in the Chebyshev Series expansion of a function». Math. Comp. 18 (86): 274–284. doi:10.1090/S0025-5718-1964-0166903-7. MR 0166903.
- Eremenko, A.; Lempert, L. (1994). «An Extremal Problem For Polynomials» (PDF). Proceedings of the American Mathematical Society. 122 (1): 191–193. doi:10.1090/S0002-9939-1994-1207536-1. MR 1207536.
- Hernandez, M. A. (2001). «Chebyshev’s approximation algorithms and applications». Computers & Mathematics with Applications. 41 (3–4): 433–445. doi:10.1016/s0898-1221(00)00286-8.
- Mason, J. C. (1984). «Some properties and applications of Chebyshev polynomial and rational approximation». Rational Approximation and Interpolation. Lecture Notes in Mathematics. Vol. 1105. pp. 27–48. doi:10.1007/BFb0072398. ISBN 978-3-540-13899-0.
- Mason, J. C.; Handscomb, D.C. (2002). Chebyshev Polynomials. Chapman and Hall/CRC. doi:10.1201/9781420036114. ISBN 978-1-4200-3611-4.
- Mathar, Richard J. (2006). «Chebyshev series expansion of inverse polynomials». Journal of Computational and Applied Mathematics. 196 (2): 596–607. arXiv:math/0403344. Bibcode:2006JCoAM.196..596M. doi:10.1016/j.cam.2005.10.013. S2CID 16476052.
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), «Orthogonal Polynomials», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
- Remes, Eugene. «On an Extremal Property of Chebyshev Polynomials» (PDF).
- Salzer, Herbert E. (1976). «Converting interpolation series into Chebyshev series by recurrence formulas». Mathematics of Computation. 30 (134): 295–302. doi:10.1090/S0025-5718-1976-0395159-3. MR 0395159.
- Scraton, R.E. (1969). «The Solution of integral equations in Chebyshev series». Mathematics of Computation. 23 (108): 837–844. doi:10.1090/S0025-5718-1969-0260224-4. MR 0260224.
- Smith, Lyle B. (1966). «Computation of Chebyshev series coefficients». Comm. ACM. 9 (2): 86–87. doi:10.1145/365170.365195. S2CID 8876563. Algorithm 277.
- Suetin, P. K. (2001) [1994], «Chebyshev polynomials», Encyclopedia of Mathematics, EMS Press
External links[edit]
Media related to Chebyshev polynomials at Wikimedia Commons
- Weisstein, Eric W. «Chebyshev polynomial[s] of the first kind». MathWorld.
- Mathews, John H. (2003). «Module for Chebyshev polynomials». Department of Mathematics. Course notes for Math 340 Numerical Analysis & Math 440 Advanced Numerical Analysis. Fullerton, CA: California State University. Archived from the original on 29 May 2007. Retrieved 17 August 2020.
- «Chebyshev interpolation: An interactive tour». Mathematical Association of America (MAA) – includes illustrative Java applet.
- «Numerical computing with functions». The Chebfun Project.
- «Is there an intuitive explanation for an extremal property of Chebyshev polynomials?». Math Overflow. Question 25534.
- «Chebyshev polynomial evaluation and the Chebyshev transform». Boost. Math.
Последовательность полиномов
Полиномы Чебышева — это две последовательности полиномов, связанных с синусом и косинусные функции, обозначенные как T n (x) и U n (x). Их можно определить несколькими способами, которые имеют одинаковый конечный результат; в этой статье полиномы определяются, начиная с тригонометрических функций :
- Полиномы Чебышева первого рода (T n) задаются как
- Tn(cos (θ)) = cos (n θ).
- Аналогичным образом определим полиномы Чебышева второго рода (U n) как
- Un(cos (θ)) sin (θ) = sin ((n + 1) θ).
Эти определения не являются полиномами как таковыми, но, используя различные триггерные тождества, они могут быть преобразованы в полиномиальные Например, для n = 2 формулу T 2 можно преобразовать в многочлен с аргументом x = cos (θ), используя формулу двойного угла:
- cos (2 θ) = 2 соз 2 (θ) — 1 { displaystyle cos (2 theta) = 2 cos ^ {2} ( theta) -1}
Заменяя термины в формуле на определения, приведенные выше, мы получаем
- T2(x) = 2 x — 1.
Остальные T n (x) определяются аналогично, где для многочленов второго рода (U n) мы должны использовать формулу де Муавра, чтобы получить sin (n θ) как sin (θ) ti является полиномом от cos (θ). Например,
- грех (3 θ) = (4 соз 2 (θ) — 1) грех (θ) { displaystyle sin (3 theta) = (4 cos ^ {2} ( theta) -1) , sin ( theta)}
дает
- U2(x) = 4x — 1.
После преобразования в полиномиальную форму T n (x) и U n (x) называются полиномами Чебышева первого и второго рода соответственно.
Важным и удобным свойством T n (x) является то, что они ортогональны по отношению к внутреннему произведению
- ⟨f ( Икс), г (Икс)⟩ знак равно ∫ — 1 1 е (Икс) г (Икс) dx 1 — Икс 2, { Displaystyle { bigl langle} , е (х), , г (х) , { bigr rangle} ~ = ~ int _ {- 1} ^ {1} , f (x) , g (x) , { frac { mathrm {d} x} {, { sqrt {1-x ^ {2} ,}} ,}} ~,}
и U n (x) ортогональны по отношению к другому аналогичному внутреннему продукту продукт, указанный ниже. Это следует из того факта, что полиномы Чебышева решают дифференциальные уравнения Чебышева
- (1 — x 2) y ″ — xy ′ + n 2 y = 0, { displaystyle (1-x ^ {2}) , y » — x , y ‘+ n ^ {2} , y = 0 ~,}
- (1 — x 2) y ″ — 3 xy ′ + n (n + 2) y = 0, { displaystyle (1-x ^ {2}) , y » — 3 , x , y ‘+ n , (n + 2) , y = 0 ~,}
которые являются Дифференциальные уравнения Штурма – Лиувилля. Общей чертой таких дифференциальных уравнений является выделенный ортонормированный набор решений. (Другой способ определить полиномы Чебышева — это решения этих уравнений.)
Полиномы Чебышева T n — это полиномы с максимально возможным старшим коэффициентом, у которых абсолютное значение на интервале [−1, 1] ограничено 1. Они также являются «экстремальными» многочленами для многих других свойств.
Многочлены Чебышева важны в теории приближений, потому что корни T n (x), которые также называются узлами Чебышева, используются в качестве точек согласования для оптимизации полиномиальной интерполяции. Результирующий полином интерполяции сводит к минимуму проблему явления Рунге и обеспечивает приближение, близкое к наилучшему полиномиальному приближению к непрерывной функции при максимальной норме, также называется критерием «минимакс ». Это приближение непосредственно приводит к методу квадратур Кленшоу – Кертиса.
. Эти многочлены были названы в честь Пафнутого Чебышева. Буква T используется из-за альтернативной транслитерации имени Чебышев как Чебышев, Чебышев (французский) или Чебышев (немецкий).
Содержание
- 1 Определение
- 1.1 Тригонометрическое определение
- 1.2 Определение уравнения Пелла
- 1.3 Произведение многочленов Чебышева
- 2 Отношения между двумя видами многочленов Чебышева
- 3 Явные выражения
- 4 Свойства
- 4.1 Симметрия
- 4.2 Корни и экстремумы
- 4.3 Дифференцирование и интегрирование
- 4.4 Ортогональность
- 4.5 Минимальная ∞-норма
- 4.6 Другие свойства
- 4.7 Обобщенные многочлены Чебышева
- 5 Примеры
- 5.1 Первый вид
- 5.2 Второй вид
- 6 В качестве базиса
- 6.1 Пример 1
- 6.2 Пример 2
- 6.3 Частичные суммы
- 6.4 Полином в форме Чебышева
- 7 Сдвинутых многочленов Чебышева
- 8 Развернутых многочленов
- 9 См. Также
- 10 Ссылки
- 11 Источники
- 12 Внешние ссылки
Определение

Многочлены Чебышева первого рода получаются из рекуррентного соотношения
- T 0 (x) = 1 T 1 (x) = x T n + 1 (x) = 2 x T n (x) — Т п — 1 (х). { Displaystyle { begin {align} T_ {0} (x) = 1 \ T_ {1} (x) = x \ T_ {n + 1} (x) = 2x , T_ {n } (x) -T_ {n-1} (x) ~. end {align}}}
Обычная производящая функция для T n равна
- ∑ п знак равно 0 ∞ Т n (Икс) tn знак равно 1 — тх 1 — 2 тх + т 2. { displaystyle sum _ {n = 0} ^ { infty} T_ {n} (x) t ^ {n} = { frac {1-tx} {1-2tx + t ^ {2}}} ~.}
Доказательство —
- Определим G ≡ ∑ n = 0 ∞ T n (x) tn = T 0 (x) + t T 1 (x) + ∑ n = 2 ∞ T n (x) tn = 1 + tx + ∑ n = 0 ∞ T n + 2 (x) tn + 2 = 1 + tx + ∑ n = 0 ∞ (2 x T n + 1 (x) — T n (x)) tn + 2 = 1 + tx + ∑ n = 0 ∞ 2 x T n + 1 (x) tn + 2 — ∑ n = 0 ∞ T n (x) tn + 2 = 1 + tx + 2 tx ∑ n = 0 ∞ T n + 1 (x) tn + 1 — t 2 ∑ n = 0 ∞ T n (x) tn = 1 + tx + 2 tx (∑ n = 0 ∞ T n (x) tn — 1) — t 2 ∑ n = 0 ∞ T n (x) tn = 1 + tx + 2 tx (G — 1) — t 2 G = 1 + tx + 2 tx G — 2 tx — t 2 GG — 2 tx G + t 2 G = 1 + tx — 2 tx G = 1 — tx 1 — 2 tx + t 2 { displaystyle { begin {align} { text {Define}} quad G Equiv sum _ {n = 0} ^ { infty} T_ { n} (x) t ^ {n} \ = T_ {0} (x) + tT_ {1} (x) + sum _ {n = 2} ^ { infty} T_ {n} (x) t ^ {n} \ = 1 + tx + sum _ {n = 0} ^ { infty} T_ {n + 2} (x) t ^ {n + 2} \ = 1 + tx + sum _ {n = 0} ^ { infty} (2xT_ {n + 1} (x) -T_ {n} (x)) t ^ {n + 2} \ = 1 + tx + sum _ {n = 0} ^ { infty} 2xT_ {n + 1} (x) t ^ {n + 2} — sum _ {n = 0} ^ { infty} T_ {n} (x) t ^ {n + 2} \ = 1 + tx + 2tx sum _ {n = 0} ^ { infty} T_ {n + 1} (x) t ^ {n + 1 } -t ^ {2} sum _ {n = 0} ^ { infty} T_ {n} (x) t ^ {n} \ = 1 + tx + 2tx ( sum _ {n = 0} ^ { infty} T_ {n} (x) t ^ {n} -1) -t ^ {2} sum _ {n = 0} ^ { infty} T_ {n} (x) t ^ {n } \ = 1 + tx + 2tx (G-1) -t ^ {2} G \ = 1 + tx + 2txG-2tx-t ^ {2} G \ G-2txG + t ^ {2 } G = 1 + tx-2tx \ G = { frac {1-tx} {, 1-2tx + t ^ {2} ,}} end {align}}}
Есть несколько других производящие функции для полиномов Чебышева; экспоненциальная производящая функция равна
- ∑ n = 0 ∞ T n (x) t n n! Знак равно 1 2 (е т (х — х 2 — 1) + е т (х + х 2 — 1)) = е т х cosh (т х 2 — 1). { displaystyle sum _ {n = 0} ^ { infty} T_ {n} (x) , { frac {; t ^ {n} ,} {n!}} = { frac {1 } {2}} left (, e ^ {, t , left (, x — { sqrt {x ^ {2} -1 ,}} , right) ,} + e ^ {t , left (, x + { sqrt {x ^ {2} -1 ,}} , right)} , right) = e ^ {t , x} , cosh left (, t , { sqrt {x ^ {2} -1 ,}} , right) ~.}
Производящая функция, имеющая отношение к двумерной теории потенциала и мультипольное расширение равно
- ∑ n = 1 ∞ T n (x) tnn = ln (1 1-2 tx + t 2). { displaystyle sum limits _ {n = 1} ^ { infty} , T_ {n} (x) , { frac {; t ^ {n} ,} {n}} = ln left ({ frac {1} {, { sqrt {1-2 , t , x + t ^ {2} ,}} ,}} right) ~.}

Многочлены Чебышева второго рода определяются рекуррентным соотношением
- U 0 (x) = 1 U 1 (х) знак равно 2 x U n + 1 (x) = 2 x U n (x) — U n — 1 (x). { Displaystyle { begin {align} U_ {0} (x) = 1 \ U_ {1} (x) = 2x \ U_ {n + 1} (x) = 2x , U_ {n } (x) -U_ {n-1} (x) ~. end {align}}}
Обратите внимание, что два набора рекуррентных отношений идентичны, за исключением T 1 (x) = x { displaystyle ~ T_ {1} (x) = x ~}

- ∑ n = 0 ∞ U n (x) tn = 1 1 — 2 tx + t 2; { displaystyle sum _ {n = 0} ^ { infty} U_ {n} (x) , t ^ {n} = { frac {1} {, 1-2tx + t ^ {2} ,}} ~;}
экспоненциальная производящая функция равна
- ∑ n = 0 ∞ U n (x) tnn! знак равно е т х (сш (т х 2 — 1) + х х 2 — 1 зп (т х 2 — 1)). { displaystyle sum _ {n = 0} ^ { infty} , U_ {n} (x) { frac {; t ^ {n} ,} {n!}} = e ^ {tx} left ( ch left (, t , { sqrt {x ^ {2} -1 ,}} , right) + { frac {x} {, { sqrt {x ^ { 2} -1 ,}} ,}} sinh left (, t , { sqrt {x ^ {2} -1 ,}} , right) , right) ~.}
Тригонометрическое определение
Как описано во введении, многочлены Чебышева первого рода можно определить как уникальные многочлены, удовлетворяющие
- T n (x) = {cos (n arccos x) если | х | ≤ 1 cosh (n arcosh x), если x ≥ 1 (- 1) n cosh (n arcosh (- x)), если x ≤ — 1 { displaystyle T_ {n} (x) = { begin { case} cos { big (} , n arccos x , { big)} quad { text {if}} ~ | x | leq 1 \ cosh { big (} n OperatorName {arcosh} x { big)} quad { text {if}} ~ x geq 1 \ (- 1) ^ {n} cosh { big (} n operatorname {arcosh} (- x) { big)} quad { text {if}} ~ x leq -1 end {cases}}}
или, другими словами, как уникальные многочлены, удовлетворяющие
- T n ( соз θ) знак равно соз (N θ) { displaystyle T_ {n} ( cos theta) = cos (n theta)}
для n = 0, 1, 2, 3,… который с технической точки зрения является вариантом (эквивалентным транспонированием) уравнения Шредера. То есть T n (x) функционально сопряжено с n x, кодифицированным в свойстве вложенности ниже. Далее сравните с полиномами распространения в разделе ниже.
Многочлены второго рода удовлетворяют:
- U n — 1 (cos θ) ⋅ sin θ = sin (n θ), { displaystyle U_ {n-1} (, cos theta ,) cdot sin theta = sin (n theta) ~,}
или
- U n (cos θ) = sin ((n + 1) θ) sin θ, { Displaystyle U_ {n} (, соз тета ,) = { гидроразрыва { sin { big (} , (п {+} 1) , theta , { big)}} { sin theta}} ~,}
который структурно очень похож на ядро Дирихле Dn(x):
- D n (x) = sin ((2 n + 1) х 2) грех х 2 = U 2 n (соз х 2). { displaystyle D_ {n} (x) = { frac { sin left (, (2n {+} 1) { dfrac {x} {2}} , right)} { sin { dfrac {, x ,} {2}}}} = U_ {2n} left (, cos { frac {, x ,} {2}} , right) ~.}
То, что cos nx является многочленом n-й степени от cos x, можно увидеть, заметив, что cos nx является действительной частью одной стороны формулы де Муавра. Действительная часть другой стороны — это многочлен от cos x и sin x, в котором все степени sin x четны и, таким образом, заменяются тождеством cos x + sin x = 1. По тем же соображениям sin nx является мнимым часть полинома, в которой все степени sin x нечетны, и, таким образом, если одна из них исключена, оставшиеся могут быть заменены, чтобы создать полином (n-1) -й степени от cos x.
Идентичность весьма полезна в сочетании с формулой рекурсивного генерирования, поскольку она позволяет вычислить косинус любого целого кратного угла исключительно в терминах косинуса основного угла.
Вычисление первых двух многочленов Чебышева:
- T 0 (cos θ) = cos 0 θ = 1 { displaystyle T_ {0} ( cos theta) = cos 0 theta = 1}
и
- T 1 (cos θ) = cos θ, { displaystyle T_ {1} ( cos theta) = cos theta,}
легко определить, что
- cos 2 θ = 2 cos θ cos θ — 1 = 2 cos 2 θ — 1 cos 3 θ = 2 cos θ cos 2 θ — cos θ = 4 cos 3 θ — 3 cos θ, { Displaystyle { begin {выровнено} cos 2 theta = 2 cos theta cos theta -1 = 2 cos ^ {2} theta -1 \ cos 3 theta = 2 cos theta cos 2 theta — cos theta = 4 cos ^ {3} theta -3 cos theta, end {align}}}
и так далее.
Два непосредственных следствия — это идентичность композиции (или свойство вложенности, определяющее полугруппу )
- T n (T m (x)) = T nm (x); { displaystyle T_ {n} { big (} , T_ {m} (x) , { big)} = T_ {nm} (x) ~;}
и выражение комплексного возведения в степень в терминах Чебышева многочлены: задано z = a + bi,
- zn = | z | n (cos (n arccos a | z |) + i sin (n arccos a | z |)) = | z | n T n (a | z |) + ib | z | n — 1 U n — 1 (a | z |). { displaystyle { begin {align} z ^ {n} = | z | ^ {n} left ( cos left (n arccos { frac {a} {| z |}} right) + i sin left (, n , arccos { frac {a} {, | z | ,}} right) , right) \ = | z | ^ {n} T_ {n} left ({ frac {a} {, | z | ,}} right) + ib | z | ^ {n-1} U_ {n-1} left ({ frac {a} {, | z | ,}} right) ~. end {align}}}
Определение уравнения Пелла
Многочлены Чебышева также могут быть определены как решения уравнения Пелла
- T n (x) 2 — (x 2 — 1) U n — 1 (x) 2 знак равно 1 { displaystyle T_ {n} (x) ^ {2} — left (, x ^ {2} -1 , right) U_ {n-1} (x) ^ {2} = 1}
в кольце R [x]. Таким образом, они могут быть сгенерированы стандартной техникой для уравнений Пелла взятия степеней фундаментального решения:
- T n (x) + U n — 1 (x) x 2 — 1 = (x + x 2 — 1) п. { displaystyle T_ {n} (x) + U_ {n-1} (x) , { sqrt {x ^ {2} -1 ,}} = left (x + { sqrt {x ^ {2) } -1 ,}} right) ^ {n} ~.}
Произведения полиномов Чебышева
При работе с полиномами Чебышева довольно часто встречаются произведения двух из них. Эти произведения могут быть сведены к комбинациям полиномов Чебышева с более низкой или более высокой степенью, и заключительные утверждения о продукте сделать легче. Предполагается, что в дальнейшем индекс m больше или равен индексу n и n не является отрицательным. Для многочленов Чебышева первого рода произведение увеличивается до
- 2 T m (x) T n (x) = T m + n (x) + T | м — п | (x) { displaystyle 2T_ {m} (x) T_ {n} (x) = T_ {m + n} (x) + T_ {| mn |} (x)}
, что является аналогом теорема сложения
- 2 соз α соз β = соз (α + β) + соз (α — β) { Displaystyle 2 соз альфа , соз бета = соз ( alpha + beta) + cos ( alpha — beta)}
с тождествами
- α ≡ m arccos x и β ≡ n arccos x. { displaystyle alpha Equiv m arccos x quad { text {and}} quad beta Equiv n arccos x ~.}
Для n = 1 это приводит к уже известной формуле повторения, просто устроены по-разному, и при n = 2 оно образует рекуррентное соотношение для всех четных или всех нечетных многочленов Чебышева (в зависимости от четности наименьшего m), что позволяет проектировать функции с заданными свойствами симметрии. Из этого разложения произведения можно заключить еще три полезные формулы для вычисления полиномов Чебышева:
- T 2 n (x) = 2 T n 2 (x) — T 0 (x) = 2 T n 2 (x) — 1 T 2 n + 1 (x) = 2 T n + 1 (x) T n (x) — T 1 (x) = 2 T n + 1 (x) T n (x) — x T 2 n — 1 (x) = 2 T n — 1 (x) T n (x) — T 1 (x) = 2 T n — 1 (x) T n (x) — x { displaystyle { begin {align} T_ {2n} (x) = 2 , T_ {n} ^ {2} (x) -T_ {0} (x) = 2T_ {n} ^ {2} (x) -1 \ T_ {2n + 1} (x) = 2 , T_ {n + 1} (x) , T_ {n} (x) -T_ {1} (x) = 2 , T_ {n + 1} (x) , T_ {n} (x) -x \ T_ {2n-1} (x) = 2 , T_ {n-1} (x) , T_ {n} (x) -T_ {1} (x) = 2 , T_ {n-1} (x) , T_ {n} (x) -x end {align}}}
Для многочленов Чебышева второго рода произведения могут быть записаны как:
- U m (x) U n (x) = ∑ k = 0 n U m — n + 2 k (x) = ∑ p = m — n шаг 2 m + n U p (x). { Displaystyle U_ {m} (x) , U_ {n} (x) = sum _ {k = 0} ^ {n} , U_ {m-n + 2k} (x) = sum _ { underset {, { text {step 2}} ,} {p = mn}} ^ {m + n} U_ {p} (x) ~.}
для m ≥ n.
Таким образом, как и выше, при n = 2 рекуррентная формула для многочленов Чебышева второго рода сводится для обоих типов симметрии к
- U m + 2 (x) = U 2 (x) U м (Икс) — U м (Икс) — U м — 2 (Икс) знак равно U м (Икс) (U 2 (Икс) — 1) — U м — 2 (Икс), { Displaystyle U_ {м + 2 } (x) = U_ {2} (x) , U_ {m} (x) -U_ {m} (x) -U_ {m-2} (x) = U_ {m} (x) , { big (} U_ {2} (x) -1 { big)} — U_ {m-2} (x) ~,}
в зависимости от того, начинается ли m с 2 или 3.
Отношения между двумя типами полиномов Чебышева
Полиномы Чебышева первого и второго видов соответствуют дополнительной паре последовательностей Люка Ṽn(P, Q) и Ũ n (P, Q) с параметрами P = 2x и Q = 1:
- U ~ n (2 x, 1) = U n — 1 (x), V ~ n (2 x, 1) = 2 T n ( Икс). { displaystyle { begin {align} { tilde {U}} _ {n} (2x, 1) = U_ {n-1} (x) ~, \ { tilde {V}} _ {n } (2x, 1) = 2 , T_ {n} (x) ~. End {align}}}
Отсюда следует, что они также удовлетворяют паре взаимных рекуррентных уравнений:
- T n + 1 (х) = х Т п (х) — (1 — х 2) U n — 1 (х), U n + 1 (х) = х U n (х) + Т п + 1 (х). { displaystyle { begin {align} T_ {n + 1} (x) = x , T_ {n} (x) — (1-x ^ {2}) , U_ {n-1} (x) ~, \ U_ {n + 1} (x) = x , U_ {n} (x) + T_ {n + 1} (x) ~. End {align}}}
Чебышевский полиномы первого и второго рода также связаны следующими соотношениями:
- T n (x) = 1 2 (U n (x) — U n — 2 (x)). Т n (x) = U n (x) — x U n — 1 (x). U n (x) = 2 ∑ odd j n T j (x) для нечетных n. U n (x) = 2 ∑ even j n T j (x) — 1 для четного n. { displaystyle { begin {align} T_ {n} (x) = { frac {1} {2}} { big (} , U_ {n} (x) -U_ {n-2} ( x) , { big)} ~. \ T_ {n} (x) = U_ {n} (x) -x , U_ {n-1} (x) ~. \ U_ { n} (x) = 2 , sum _ {{ text {odd}} j} ^ {n} T_ {j} (x) { text {for odd}} n ~. \ U_ { n} (x) = 2 , sum _ {{ text {even}} j} ^ {n} T_ {j} (x) -1 { text {for even}} n ~. end { выровнены}}}
Рекуррентное соотношение производной полиномов Чебышева может быть получено из этих соотношений:
- 2 T n (x) = 1 n + 1 ddx T n + 1 (x) — 1 n — 1 ddx T n — 1 (x) n = 2, 3,… { displaystyle 2 , T_ {n} (x) = { frac {1} {, n + 1 ,}} , { frac { mathrm {d}} {, mathrm {d} x ,}} T_ {n + 1} (x) — { frac {1} {, n-1 ,}} , { frac { mathrm {d}} {, mathrm {d} x ,}} , T_ {n-1} (x) qquad n = 2,3, ldots}
Это соотношение используется в спектральном методе Чебышева решения дифференциальных уравнений.
Неравенства Турана для полиномов Чебышева равны
- T n (x) 2 — T n — 1 (x) T n + 1 (x) = 1 — x 2>0 для — 1 < x < 1 and U n ( x) 2 − U n − 1 ( x) U n + 1 ( x) = 1>0. { displaystyle { begin {align} T_ {n} (x) ^ {2} -T_ {n-1} (x) , T_ {n + 1} (x) = 1-x ^ {2}>0 { text {for}} — 1 0 ~. End {выровнено}}}
Интегральные отношения являются
- ∫ — 1 1 T n (y) dy (y — x) 1 — y 2 = π U n — 1 (x), ∫ — 1 1 1 — y 2 U n — 1 (y) dyy — Икс = — π T N (Икс) { Displaystyle { begin {align} int _ {- 1} ^ {1} { frac {T_ {n} (y) , mathrm {d} y} { , (yx) , { sqrt {1-y ^ {2} ,}} ,}} = pi , U_ {n-1} (x) ~, \ int _ {- 1} ^ {1} { frac {{ sqrt {, 1-y ^ {2} ,}} , U_ {n-1} (y) , mathrm {d} y ,} { yx}} = — pi , T_ {n} (x) end {align}}}
где интегралы считаются главным значением.
Явные выражения
Разные подходы к определению полиномов Чебышева приводят к различным явным выражениям, таким как:
- T n (x) = {cos (n arccos x) для | x | ≤ 1 1 2 ((x — x 2 — 1) n + (х + x 2 — 1) n) для | х | ≥ 1 = {cos (n arccos x) для — 1 ≤ x ≤ 1 ch (n arcosh x) для 1 ≤ x (- 1) n ch (n arcosh (- x)) для x ≤ — 1 T n (x) = ∑ k = 0 ⌊ n 2 ⌋ (n 2 k) (x 2 — 1) kxn — 2 k = xn ∑ k = 0 ⌊ n 2 ⌋ (n 2 k) (1 — x — 2) К знак равно N 2 ∑ К знак равно 0 ⌊ N 2 ⌋ (- 1) К (N — К — 1)! к! (п — 2 к)! (2 x) n — 2 k, если n>0 = n ∑ k = 0 n (- 2) k (n + k — 1)! (п — к)! (2 к)! (1 — x) k для n>0 = 2 F 1 (- n, n; 1 2; 1 2 (1 — x)) { displaystyle { begin {align} T_ {n} (x) = { begin {case} cos (n arccos x) qquad { text {for}} ~ | x | leq 1 \\ { dfrac {1} {2}} { bigg (} { Big (} x — { sqrt {x ^ {2} -1}} { Big)} ^ {n} + { Big (} x + { sqrt {x ^ {2} -1}} { Big)} ^ {n} { bigg)} qquad { text {for}} ~ | x | geq 1 \ end {cases}} \\ = { begin {cases} cos (n arccos x) qquad quad { text {for}} ~ -1 leq x leq 1 \\ cosh (n operatorname {arcosh} x) qquad quad { текст {for}} ~ 1 leq x \\ (- 1) ^ {n} cosh { big (} n operatorname {arcosh} (-x) { big)} qquad quad { text {for}} ~ x leq -1 \ end {case}} \\\ T_ {n} (x) = sum _ {k = 0} ^ { left lfloor { frac {n} {2}} right rfloor} { binom {n} {2k}} left (x ^ {2} -1 right) ^ {k} x ^ {n-2k} \ = x ^ {n} sum _ {k = 0} ^ { left lfloor { frac {n} {2}} right rfloor} { binom {n} {2k}} left (1 -x ^ {- 2} right) ^ {k} \ = { frac {n} {2}} sum _ {k = 0} ^ { left lfloor { frac {n} {2 }} right rfloor} (- 1) ^ {k} { frac {(nk-1)!} {k! (n-2k)!}} ~ (2x) ^ {n-2k} qquad qquad { text {for}} ~ n>0 \\ = n sum _ {k = 0} ^ {n} (- 2) ^ {k} { frac {(n + k-1)!} {(nk)! (2k)!}} (1-x) ^ {k} qquad qquad ~ { text {for}} ~ n>0 \ = {} _ {2} F_ {1} left (-n, n; { tfrac {1} {2}}; { tfrac {1} {2}} (1-x) справа) \ конец {выровнен}}}
с обратным
- xn = 2 1 — n ∑ ′ j = 0, n — jevenn (nn — j 2) T j (x), { displaystyle x ^ {n} = 2 ^ {1-n} mathop {{ sum} ‘} _ {j = 0, , nj , mathrm {even}} ^ {n} { binom {n} { tfrac {nj} {2}}} T_ {j} (x),}
где штрих у символа суммы указывает, что вклад j = 0 необходимо уменьшить вдвое, если он появляется.
- U n (x) = (x + x 2 — 1) n + 1 — (x — x 2 — 1) n + 1 2 x 2 — 1 = ∑ k = 0 ⌊ n 2 ⌋ (n + 1 2 k + 1) (x 2 — 1) kxn — 2 k = xn ∑ k = 0 ⌊ n 2 ⌋ (n + 1 2 k + 1) (1 — x — 2) k = ∑ k = 0 ⌊ n 2 ⌋ (2 k — (n + 1) k) (2 x) n — 2 k для n>0 = ∑ k = 0 ⌊ n 2 ⌋ (- 1) k (n — kk) (2 x) n — 2 k для n>0 = ∑ k = 0 n (- 2) k (n + k + 1)! (п — к)! (2 к + 1)! (1 — x) k для n>0 = (n + 1) 2 F 1 (- n, n + 2; 3 2; 1 2 (1 — x)) { displaystyle { begin {align} U_ {n } (x) = { frac { left (x + { sqrt {x ^ {2} -1}} right) ^ {n + 1} — left (x — { sqrt {x ^ {2 } -1}} right) ^ {n + 1}} {2 { sqrt {x ^ {2} -1}}}} \ = sum _ {k = 0} ^ { left lfloor { frac {n} {2}} right rfloor} { binom {n + 1} {2k + 1}} left (x ^ {2} -1 right) ^ {k} x ^ {n -2k} \ = x ^ {n} sum _ {k = 0} ^ { left lfloor { frac {n} {2}} right rfloor} { binom {n + 1} { 2k + 1}} left (1-x ^ {- 2} right) ^ {k} \ = sum _ {k = 0} ^ { left lfloor { frac {n} {2} } right rfloor} { binom {2k- (n + 1)} {k}} ~ (2x) ^ {n-2k} { text {for}} ~ n>0 \ = sum _ {k = 0} ^ { left lfloor { frac {n} {2}} right rfloor} (- 1) ^ {k} { binom {nk} {k}} ~ (2x) ^ {n-2k} { text {for}} ~ n>0 \ = sum _ {k = 0} ^ {n} (- 2) ^ {k} { frac {(n + k + 1)!} {(Nk)! (2k + 1)!}} (1-x) ^ {k} { text {for}} ~ n>0 \ = (n + 1) {} _ {2} F_ {1} left (-n, n + 2; { tfrac {3} {2}}; { tfrac {1} {2}} (1-x) right) \ конец {выровнен}}}
где 2F1- это гипергеометрическая функция.
Свойства
Симметрия
- T n (- x) = (- 1) n T n (x) = {T n (x) для четного n — T n (x) для нечетного n U n (- x) = (- 1) n U n (x) = {U n (x) для четного n — U n (x) для n нечетного { displaystyle { begin {выровнено} T_ {n} (- x) = (- 1) ^ {n} T_ {n} (x) \ = { begin {cases} T_ {n} (x) quad ~ { text {for}} ~ n ~ { text {even}} \\ — T_ {n} (x) quad ~ { text {for}} ~ n ~ { text {odd}} end {case}} \\\ U_ {n} (- x) = (- 1) ^ { n} U_ {n} (x) \\ = { begin {cases} U_ {n} (x) quad ~ { text {for}} ~ n ~ { text {even}} \ — U_ {n} (x) quad ~ { text {for}} ~ n ~ { text {odd}} end {case}} \ end {align}}}
То есть полиномы Чебышева четного порядка имеют четную симму попробуйте и содержат только четные степени x. Многочлены Чебышева нечетного порядка имеют нечетную симметрию и содержат только нечетные степени x.
Корни и экстремумы
Многочлен Чебышева любого вида со степенью n имеет n различных простых корней, называемых корнями Чебышева, в интервале [−1, 1]. Корни полинома Чебышева первого рода иногда называют узлами Чебышева, потому что они используются как узлы при полиномиальной интерполяции. Используя тригонометрическое определение и тот факт, что
- cos ((2 k + 1) π 2) = 0 { displaystyle cos left ((2k + 1) { frac { pi} {2}} right) = 0}
можно показать, что корни T n равны
- xk = cos (π (k + 1/2) n), k = 0,…, n — 1. { displaystyle x_ {k} = cos left ({ frac { pi (k + 1/2)} {n}} right), quad k = 0, ldots, n-1.}
Аналогично, корни U n равны
- xk = cos (kn + 1 π), k = 1,…, n. { displaystyle x_ {k} = cos left ({ frac {k} {n + 1}} pi right), quad k = 1, ldots, n.}
экстремумы из T n на интервале −1 ≤ x ≤ 1 расположены в
- xk = cos (kn π), k = 0,…, n. { displaystyle x_ {k} = cos left ({ frac {k} {n}} pi right), quad k = 0, ldots, n.}
Одно уникальное свойство чебышевских полиномы первого рода состоят в том, что на интервале −1 ≤ x ≤ 1 все экстремумы имеют значения, равные −1 или 1. Таким образом, эти многочлены имеют только два конечных критических значения, определяющее свойство многочленов Шабата. И первый, и второй виды полиномов Чебышева имеют экстремумы на концах, задаваемые следующим образом:
- T n (1) = 1 { displaystyle T_ {n} (1) = 1}
- T n (- 1) Знак равно (- 1) n { displaystyle T_ {n} (- 1) = (- 1) ^ {n}}
- U n (1) = n + 1 { displaystyle U_ {n} (1) = n + 1}
- U n (- 1) = (- 1) n (n + 1). { displaystyle U_ {n} (- 1) = (- 1) ^ {n} , (n + 1) ~.}
Дифференцирование и интегрирование
Производные полиномов могут быть меньше чем прямолинейно. Дифференцируя полиномы в их тригонометрической форме, можно показать, что:
- d T ndx = n U n — 1 d U ndx = (n + 1) T n + 1 — x U nx 2 — 1 d 2 T ndx 2 знак равно nn T n — x U n — 1 x 2 — 1 знак равно n (n + 1) T n — U nx 2 — 1. { Displaystyle { begin {align} { frac { mathrm {d} T_ {n}} { mathrm {d} x}} = nU_ {n-1} \ { frac { mathrm {d } U_ {n}} { mathrm {d} x}} = { frac {(n + 1) T_ {n + 1} -xU_ {n}} {x ^ {2} -1}} \ { frac { mathrm {d} ^ {2} T_ {n}} { mathrm {d} x ^ {2}}} = n { frac {nT_ {n} -xU_ {n-1}} {x ^ {2} -1}} = n { frac {(n + 1) T_ {n} -U_ {n}} {x ^ {2} -1}}. end {align}}}
Последние две формулы могут быть затруднительны в числовом отношении из-за деления на ноль (0/0 неопределенная форма, в частности) при x = 1 и x = −1. Можно показать, что:
- d 2 T n d x 2 | x = 1 = n 4 — n 2 3, d 2 T n d x 2 | Икс = — 1 знак равно (- 1) N N 4 — N 2 3. { displaystyle { begin {align} left. { frac { mathrm {d} ^ {2} T_ {n}} { mathrm {d} x ^ {2}}} right | _ {x = 1} ! ! = { Frac {n ^ {4} -n ^ {2}} {3}}, \ left. { Frac { mathrm {d} ^ {2} T_ {n }} { mathrm {d} x ^ {2}}} right | _ {x = -1} ! ! = (- 1) ^ {n} { frac {n ^ {4} -n ^ {2}} {3}}. End {align}}}
Доказательство —
Вторая производная от полинома Чебышева первого рода равна
- T n ″ = nn T n — x U n — 1 x 2 — 1 { displaystyle T » _ {n} = n { frac {nT_ {n} -xU_ {n-1}} {x ^ {2} -1}}}
, который при оценке, как показано выше, создает проблему, поскольку неопределенно при x = ± 1. Поскольку функция является полиномом, (все) производные должны существовать для всех действительных чисел, поэтому ограничение приведенного выше выражения должно дать желаемое значение:
- T n ″ (1) = lim x → 1 nn T n — x U n — 1 x 2 — 1 { displaystyle T » _ {n} (1) = lim _ {x to 1} n { frac {nT_ {n} -xU_ {n-1 }} {x ^ {2} -1}}}
где пока рассматривается только x = 1. Разложим знаменатель на множители:
- T n ″ (1) = lim x → 1 nn T n — x U n — 1 (x + 1) (x — 1) = lim x → 1 nn T n — x U n — 1 х — 1 х + 1. { displaystyle T » _ {n} (1) = lim _ {x to 1} n { frac {nT_ {n} -xU_ {n-1}} {(x + 1) (x-1)}} = lim _ {x to 1} n { frac {; { dfrac {nT_ {n} -xU_ {n-1}} {x-1}} ;} {x + 1} }.}
Поскольку предел в целом должен существовать, предел числителя и знаменателя должны существовать независимо, и
- T n ″ (1) = n lim x → 1 n T n — x U n — 1 x — 1 lim x → 1 (x + 1) знак равно n 2 lim x → 1 n T n — x U n — 1 x — 1. { displaystyle T » _ {n} (1) = n { frac { displaystyle { lim _ {x to 1}} { frac {nT_ {n} -xU_ {n-1}} {x -1}}} { displaystyle { lim _ {x to 1}} (x + 1)}} = { frac {n} {2}} lim _ {x to 1} { frac { nT_ {n} -xU_ {n-1}} {x-1}}.}
Знаменатель (все еще) ограничивается нулем, что означает, что числитель должен ограничиваться нулем, то есть U n — 1 (1) = nT n (1) = n, что будет полезно позже. Поскольку числитель и знаменатель ограничиваются нулем, применяется правило Л’Опиталя :
- T n ″ (1) = n 2 lim x → 1 ddx (n T n — x U n — 1) ddx (x — 1) = n 2 lim x → 1 ddx (n T n — x U n — 1) = n 2 lim x → 1 (n 2 U n — 1 — U n — 1 — xddx (U n — 1)) = n 2 (n 2 U n — 1 (1) — U n — 1 (1) — lim x → 1 xddx (U n — 1)) = n 4 2 — n 2 2 — 1 2 lim x → 1 ddx (n U n — 1) = n 4 2 — n 2 2 — T n ″ (1) 2 T n ″ (1) = n 4 — n 2 3. { displaystyle { begin {align} T » _ {n} (1) = { frac {, n ,} {2}} , lim _ {x to 1} , { frac {, { frac { mathrm {d}} {, mathrm {d} x ,}} , left (n , T_ {n} -x , U_ {n-1} справа) ,} {, { frac { mathrm {d}} {, mathrm {d} x ,}} , (x-1) ,}} \ = { frac { n} {2}} lim _ {x to 1} { frac { mathrm {d}} {, mathrm {d} x ,}} , left (n , T_ {n} -x , U_ {n-1} right) \ = { frac {n} {2}} lim _ {x to 1} left (; n ^ {2} , U_ { n-1} -U_ {n-1} -x { frac { mathrm {d}} {, mathrm {d} x ,}} , left (U_ {n-1} right) ; right) \ = { frac {n} {2}} left (, n ^ {2} , U_ {n-1} (1) -U_ {n-1} (1) — lim _ {x to 1} x , { frac { mathrm {d}} {, mathrm {d} x ,}} , left (U_ {n-1} right) , right) \ = { frac {; n ^ {4} ,} {2}} — { frac {, ; n ^ {2} ,} {2}} — { frac {1} {, 2 ,}} lim _ {x to 1} { frac { mathrm {d}} {, mathrm {d} x ,}} , left ( n , U_ {n-1} right) \ = { frac {; n ^ {4} ,} {2}} — { frac {; n ^ {2} ,} { 2}} — { frac {, T » _ {n} (1) ,} {2}} \ T » _ {n} (1) = { frac {, n ^ { 4} -n ^ {2} ,} {3}} ~. \ end {выравнивание}}
Доказательство для x = −1 аналогично, с тем фактом, что T n (- 1) = (−1) важно.
Действительно, имеет место следующая более общая формула:
- d p T n d x p | Икс знак равно ± 1 знак равно (± 1) N + р ∏ К знак равно 0 п — 1 N 2 — К 2 2 К + 1. { displaystyle left. { frac {d ^ {p} T_ {n}} {dx ^ {p}}} right | _ {x = pm 1} ! ! = ( pm 1) ^ {n + p} prod _ {k = 0} ^ {p-1} { frac {, n ^ {2} -k ^ {2} ,} {2k + 1}} ~.}
Этот последний результат очень полезен при численном решении задач на собственные значения.
- dpdxp T n (x) = 2 pn ∑ ′ 0 ≤ k ≤ n — p, n — p — k даже (n + p — k 2-1 n — p — k 2) (n + p + к 2 — 1)! (п — р + к 2)! T К (Икс), п ≥ 1, { Displaystyle { frac { mathrm {d} ^ {p}} {, mathrm {d} x ^ {p} ,}} T_ {n} (х) = 2 ^ {p} , n mathop {{ sum} ‘} _ {0 leq k leq np, , npk { text {even}}} { binom {{ frac {, n + pk ,} {2}} — 1} { frac {, npk ,} {2}}} { frac { left ({ frac {, n + p + k ,} { 2}} — 1 right)!} {, Left ({ frac {, n-p + k ,} {2}} right)! ,}} , T_ {k} (x) ~, qquad p geq 1 ~,}
где штрих у символов суммирования означает, что член, вносимый k = 0, должен быть уменьшен вдвое, если он появляется.
Concerning integration, the first derivative of the Tnimplies that
- ∫ U n d x = T n + 1 n + 1 {displaystyle int U_{n},mathrm {d} x={frac {,T_{n+1},}{n+1}}}
and the recurrence relation for the first kind polynomials involving derivatives establishes that for n ≥ 2
- ∫ T n d x = 1 2 ( T n + 1 n + 1 − T n − 1 n − 1) = n T n + 1 n 2 − 1 − x T n n − 1. {displaystyle int T_{n},mathrm {d} x={frac {1}{2}},left(,{frac {,T_{n+1},}{n+1}}-{frac {,T_{n-1},}{n-1}},right)={frac {,n,T_{n+1},}{n^{2}-1}}-{frac {,x,T_{n},}{n-1}}~.}
The latter formula can be further manipulated to express the integral of Tnas a function of Chebyshev polynomials of the first kind only:
- ∫ T n d x = n n 2 − 1 T n + 1 − 1 n − 1 T 1 T n = n n 2 − 1 T n + 1 − 1 2 ( n − 1) ( T n + 1 + T n − 1) = 1 2 ( n + 1) T n + 1 − 1 2 ( n − 1) T n − 1. {displaystyle int T_{n},mathrm {d} x={frac {n}{n^{2}-1}}T_{n+1}-{frac {1}{n-1}}T_{1}T_{n}={frac {n}{,n^{2}-1,}},T_{n+1}-{frac {1}{,2(n-1),}},(T_{n+1}+T_{n-1})={frac {1}{,2(n+1),}},T_{n+1}-{frac {1}{,2(n-1),}},T_{n-1}~.}
Furthermore, we have
- ∫ − 1 1 T n ( x) d x = { ( − 1) n + 1 1 − n 2 if n ≠ 1 0 if n = 1. {displaystyle int _{-1}^{1}T_{n}(x),mathrm {d} x={begin{cases}{frac {,(-1)^{n}+1,}{,1-n^{2},}}quad {text{ if }}~nneq 1\0quad {text{ if }}~n=1end{cases}}~.}
Orthogonality
Both Tnand Unform a sequence of orthogonal polynomials. The polynomials of the first kind Tnare orthogonal with respect to the weight
- 1 1 − x 2, {displaystyle {frac {1}{,{sqrt {1-x^{2},}},}}~,}
on the interval [−1, 1], i.e. we have:
- ∫ − 1 1 T n ( x) T m ( x) d x 1 − x 2 = { 0 if n ≠ m, π if n = m = 0, π 2 if n = m ≠ 0. {displaystyle int _{-1}^{1}T_{n}(x),T_{m}(x),{frac {mathrm {d} x}{,{sqrt {1-x^{2},}},}}={begin{cases}~~0quad ~{text{ if }}~nneq m~,\\~pi quad ~{text{ if }}~n=m=0~,\\~{frac {pi }{2}}quad ~{text{ if }}~n=mneq 0~.end{cases}}}
This can be proven by letting x = cos θ and using the defining identity Tn(cos θ) = cos nθ.
Similarly, the polynomials of the second kind Unare orthogonal with respect to the weight
- 1 − x 2 {displaystyle {sqrt {1-x^{2},}}}
on the interval [−1, 1], i.e. we have:
- ∫ − 1 1 U n ( x) U m ( x) 1 − x 2 d x = { 0 if n ≠ m, π 2 if n = m. {displaystyle int _{-1}^{1}U_{n}(x),U_{m}(x),{sqrt {1-x^{2},}},mathrm {d} x={begin{cases}~~0quad ~{text{ if }}~nneq m~,\~{frac {,pi ,}{2}}quad ~{text{ if }}~n=m~.end{cases}}}
(The measure √1 − x dx is, to within a normalizing constant, the Wigner semicircle distribution.)
The Tnalso satisfy a discrete orthogonality condition:
- ∑ k = 0 N − 1 T i ( x k) T j ( x k) = { 0 if i ≠ j, N if i = j = 0, N 2 if i = j ≠ 0, {displaystyle sum _{k=0}^{N-1}{T_{i}(x_{k}),T_{j}(x_{k})}={begin{cases}~0quad ~{text{ if }}~ineq j~,\~Nquad ~{text{ if }}~i=j=0~,\~{frac {,N,}{2}}quad ~{text{ if }}~i=jneq 0~,end{cases}}}
where N is any integer greater than i+j, and the xkare the N Chebyshev nodes (see above) of TN(x):
- x k = cos ( π 2 k + 1 2 N) for k = 0, 1, …, N − 1. {displaystyle x_{k}=cos left(,pi ,{frac {,2k+1,}{2N}},right)quad ~{text{ for }}~k=0,1,dots,N-1~.}
For the polynomials of the second kind and any integer N>i+j with the same Chebyshev nodes xk, there are similar sums:
- ∑ k = 0 N − 1 U i ( x k) U j ( x k) ( 1 − x k 2) = { 0 if i ≠ j, N 2 if i = j, {displaystyle sum _{k=0}^{N-1}{U_{i}(x_{k}),U_{j}(x_{k})left(1-x_{k}^{2}right)}={begin{cases}~0quad {text{ if }}~ineq j~,\~{frac {,N,}{2}}quad ~{text{ if }}~i=j~,end{cases}}}
and without the weight function:
- ∑ k = 0 N − 1 U i ( x k) U j ( x k) = { 0 if i ≢ j ( mod 2), N ⋅ ( 1 + min { i, j }) if i ≡ j ( mod 2). {displaystyle sum _{k=0}^{N-1}{U_{i}(x_{k}),U_{j}(x_{k})}={begin{cases}~0quad ~{text{ if }}~inot equiv j{pmod {2}}~,\~Ncdot (1+min{i,j})quad ~{text{ if }}~iequiv j{pmod {2}}~.end{cases}}}
For any integer N>i+j, based on the N zeros of UN(x):
- y k = cos ( π k + 1 N + 1) for k = 0, 1, …, N − 1, {displaystyle y_{k}=cos left(,pi ,{frac {k+1}{,N+1,}},right)quad ~{text{ for }}~k=0,1,dots,N-1~,}
one can get the sum:
- ∑ k = 0 N − 1 U i ( y k) U j ( y k) ( 1 − y k 2) = { 0 if i ≠ j, N + 1 2 if i = j, {displaystyle sum _{k=0}^{N-1}{U_{i}(y_{k}),U_{j}(y_{k})(1-y_{k}^{2})}={begin{cases}~0quad ~{text{ if }}ineq j~,\~{frac {,N+1,}{2}}quad ~{text{ if }}i=j~,end{cases}}}
and again without the weight function:
- ∑ k = 0 N − 1 U i ( y k) U j ( y k) = {0, если i ≢ j (mod 2), (min {i, j} + 1) (N — max {i, j}), если i ≡ j (mod 2). { displaystyle sum _ {k = 0} ^ {N-1} {U_ {i} (y_ {k}) , U_ {j} (y_ {k})} = { begin {cases} ~ 0 quad ~ { text {if}} ~ я not Equiv j { pmod {2}} ~, \ ~ { big (} min {i, j } + 1 { big) } { big (} N- max {i, j } { big)} quad ~ { text {if}} ~ i Equiv j { pmod {2}} ~. end { case}}}
Минимальная ∞-норма
Для любого заданного n ≥ 1 среди многочленов степени n со старшим коэффициентом 1 (monic многочленов),
- f ( Икс) знак равно 1 2 N — 1 T N (Икс) { Displaystyle F (х) = { гидроразрыва {1} {, 2 ^ {п-1} ,}} , T_ {п} (х) }
тот, у которого максимальное абсолютное значение на интервале [-1, 1] минимально.
Это максимальное абсолютное значение равно
- 1 2 n — 1 { displaystyle { frac {1} {2 ^ {n-1}}}}
и | f (x) | достигает этого максимума ровно n + 1 раз при
- x = cos k π n для 0 ≤ k ≤ n. { displaystyle x = cos { frac {k pi} {n}} quad { text {for}} 0 leq k leq n.}
Доказательство —
Предположим что w n (x) — многочлен степени n с ведущим коэффициентом 1 с максимальным абсолютным значением на интервале [−1,1] меньше 1/2.
Определить
- fn (x) = 1 2 n — 1 T n (x) — wn (x) { displaystyle f_ {n} (x) = { frac {1} {, 2 ^ {n-1} , }} , T_ {n} (x) -w_ {n} (x)}
Потому что в крайних точках T n мы имеем
- | w n (x) | < | 1 2 n − 1 T n ( x) | f n ( x)>0 для x = cos 2 k π n, где 0 ≤ 2 k ≤ nfn (x) < 0 for x = cos ( 2 k + 1) π n where 0 ≤ 2 k + 1 ≤ n {displaystyle {begin{aligned}|w_{n}(x)|<left|{frac {1}{2^{n-1}}}T_{n}(x)right|\f_{n}(x)>0 qquad { text {for}} ~ x = cos { frac {2k pi} { n}} ~ { text {where}} 0 leq 2k leq n \ f_ {n} (x) <0qquad {text{ for }}~x=cos {frac {(2k+1)pi }{n}}~{text{ where }}0leq 2k+1leq nend{aligned}}}
Из теоремы о промежуточном значении, f n (x) имеет не менее n корней. Однако это невозможно, поскольку f n (x) является многочленом степени n — 1, поэтому основная теорема алгебры подразумевает, что у него не более n — 1 корней.
Замечание: По теореме Эквиосколции среди всех многочленов степени ≤ n многочлен f минимизирует || f || ∞ на [−1,1], если и только если имеется n + 2 точек −1 ≤ x 0< x1<… < xn + 1 ≤ 1 таких, что | f (x i) | = || f || ∞.
Конечно, нулевой многочлен на интервале [−1,1] может быть найден сам по себе и минимизирует ∞-норму.
Однако выше | f | достигает своего максимума только n + 1 раз, потому что мы ищем лучший многочлен степени n ≥ 1 (поэтому приведенная ранее теорема не может быть использована).
Другие свойства
Многочлены Чебышева являются частным случаем ультрасферических или многочленов Гегенбауэра, которые сами по себе являются частным случаем многочленов Якоби :
- T n (x) = n 2 lim q → 0 1 q C n (q) (x), если n ≥ 1, U n (x) = n + 1 (n + 1 2 n) P n (1 2, 1 2) (х) = n + 1 (n + 1 2 n) C n (1) (x). { displaystyle { begin {align} T_ {n} (x) = { frac {n} {2}} lim _ {q to 0} { frac {1} {, q ,} } , C_ {n} ^ {(q)} (x) qquad ~ { text {if}} ~ n geq 1 ~, \\ U_ {n} (x) = { frac { n + 1} {, {n + { tfrac {1} {2}} choose n} ,}} P_ {n} ^ {({ tfrac {1} {2}}, { frac {1 } {2}})} (x) = { frac {n + 1} {, {n + { tfrac {1} {2}} choose n} ,}} C_ {n} ^ {(1)} (x) ~. end {align}}}
Для любого неотрицательного целого n, T n (x) и U n (x) оба являются полиномами от степень n. Они являются четными или нечетными функциями от x, поскольку n четное или нечетное, поэтому, когда они записываются как полиномы от x, они имеют только четные или нечетные члены степени соответственно. Фактически,
- T 2 n (x) = T n (2 x 2 — 1) = 2 T n (x) 2 — 1 { displaystyle T_ {2n} (x) = T_ {n} left ( 2x ^ {2} -1 right) = 2T_ {n} (x) ^ {2} -1}
и
- 2 x U n (1-2 x 2) = (- 1) n U 2 п + 1 (х). { displaystyle 2xU_ {n} left (, 1-2x ^ {2} , right) = (- 1) ^ {n} , U_ {2n + 1} (x) ~.}
Старший коэффициент T n равен 2, если 1 ≤ n, и 1, если 0 = n.
Tnявляются частным случаем кривых Лиссажу с отношением частот, равным n.
Некоторые последовательности полиномов, такие как полиномы Люка (Ln), полиномы Диксона (Dn), полиномы Фибоначчи (Fn), связаны с полиномами Чебышева T n и U n.
Многочлены Чебышева первого рода удовлетворяют соотношению
- T j (x) T k (x) = 1 2 (T j + k (x) + T | k — j | (x)), ∀ J, К ≥ 0, { Displaystyle T_ {j} (x) , T_ {k} (x) = { tfrac {1} {2}} left (, T_ {j + k } (x) + T_ {| kj |} (x) , right) ,, qquad forall j, k geq 0 ~,}
что легко доказывается из продукта-в -сумма для косинуса. Многочлены второго рода удовлетворяют аналогичному соотношению
- T j (x) U k (x) = {1 2 (U j + k (x) + U k — j (x)), если k ≥ j — 1, 1 2 (U j + k (x) — U j — k — 2 (x)), если k ≤ j — 2. { displaystyle T_ {j} (x) , U_ {k} (x) = { begin {cases} { tfrac {1} {2}} left (, U_ {j + k} (x) + U_ {kj} (x) , right), quad ~ { text {if}} ~ k geq j-1 ~, \\ { tfrac {1} {2}} left (, U_ {j + k} (x) -U_ {jk-2} (x) , right), quad ~ { text {if}} ~ k leq j-2 ~. End {case}}}
(с определением U −1 ≡ 0 по соглашению).
Аналогично формуле
- T n (cos θ) = cos (n θ), { displaystyle T_ {n} ( cos theta) = cos (n theta) ~,}
имеем аналогичную формулу
- T 2 n + 1 (sin θ) = (- 1) n sin ((2 n + 1) θ). { Displaystyle T_ {2n + 1} ( sin theta) = (- 1) ^ {n} sin { big (} , (2n + 1) theta , { big)} ~.}
Для x ≠ 0,
- T n (x + x — 1 2) = xn + x — n 2 { displaystyle T_ {n} left ({ frac {, x + x ^ {- 1} ,} {2}} right) = { frac {, x ^ {n} + x ^ {- n} ,} {2}}}
и
- xn = T n (Икс + Икс — 1 2) + Икс — Икс — 1 2 U N — 1 (Икс + Икс — 1 2), { Displaystyle x ^ {n} = T_ {n} left (, { frac { , x + x ^ {- 1} ,} {2}} , right) + { frac {, xx ^ {- 1} ,} {2}} U_ {n-1} left (, { frac {, x + x ^ {- 1} ,} {2}} , right) ~,}
что следует из того факта, что это верно по определению для x = e.
Определите
- C n (x) ≡ 2 T n (x 2). { Displaystyle C_ {n} (x) Equiv 2T_ {n} left (, { frac {, x ,} {2}} , right) ~.}
Тогда C n (x) и C m (x) — коммутирующие многочлены:
- C n (C m (x)) = C m (C n (x)), { displaystyle C_ {n} { big (} , C_ {m} (x) , { big)} = C_ {m} { big (} , C_ {n} (x) , { big) } ~,}
как видно из свойства абелева вложенности, указанного выше.
Обобщенные многочлены Чебышева
Обобщенные многочлены Чебышева T a определяются как
- T a (cos x) = 2 F 1 (a, — a; 1 2; 1 2 (1 — соз х)) = соз ах, x ∈ (- π, π), { displaystyle T_ {a} ( cos x) = {} _ {2} F_ {1} left (, a, -a; { tfrac {1} {2}}; { tfrac {1} {2}} (1- cos x) , right) = cos ax ,, qquad x in (- pi, pi) ~,}
где a не обязательно является целым числом, а 2F1(a, b; c; z) — гипергеометрическая функция Гаусса ; например, T 1/2 (x) = 1 + x 2 { displaystyle T_ {1/2} (x) = { sqrt { frac {1 + x} {2}}}}
- T a (x) = cos (π a 2) + a ∑ j = 1 (2 x) j 2 j cos (π (a — j) 2) (a + j — 2 2 j — 1) { displaystyle T_ {a} (x) = cos left ({ frac { pi a} {2}} right) + a sum _ {j = 1} { frac { (2x) ^ {j}} {2j}} cos left (, { frac {, pi , (aj) ,} {2}} , right) {{ frac {, a + j-2 ,} {2}} choose j-1}}
сходится для x ∈ [- 1, 1]. { displaystyle x in [-1,1] ~.}
Примеры
Первый вид

Первые несколько полиномов Чебышева первого рода OEIS : A028297
- T 0 (x) = 1 T 1 (x) = x T 2 (x) = 2 x 2 — 1 T 3 (x) = 4 x 3 — 3 x T 4 (x) = 8 x 4 — 8 x 2 + 1 T 5 (x) = 16 x 5 — 20 x 3 + 5 x T 6 (x) = 32 x 6 — 48 x 4 + 18 x 2 — 1 T 7 (x) = 64 x 7 — 112 x 5 + 56 x 3 — 7 x T 8 (x) = 128 x 8 — 256 x 6 + 160 x 4 — 32 x 2 + 1 T 9 (x) = 256 x 9 — 576 x 7 + 432 x 5 — 120 x 3 + 9 x T 10 (x) = 512 x 10 — 1280 x 8 + 1120 x 6 — 400 x 4 + 50 x 2 — 1 T 11 (x) = 1024 x 11 — 2816 x 9 + 2816 x 7 — 1232 x 5 + 220 x 3 — 11 x { displaystyle { begin {align} T_ {0} (x) = 1 \ T_ {1} (x) = x \ T_ {2} (x) = 2x ^ {2} -1 \ T_ {3} (x) = 4x ^ {3} -3x \ T_ {4} (x) = 8x ^ {4} -8x ^ {2} +1 \ T_ {5} (x) = 16x ^ {5} -20x ^ {3} + 5x \ T_ {6} (x) = 32x ^ {6} -48x ^ {4} + 18x ^ {2} -1 \ T_ {7} (x) = 64x ^ {7} -112x ^ {5} + 56x ^ {3 } -7x \ T_ {8} (x) = 128x ^ {8} -256x ^ {6} + 160x ^ {4} -32x ^ {2} +1 \ T_ {9} (x) = 256x ^ {9} -576x ^ {7} + 432x ^ {5} -120x ^ {3} + 9x \ T_ {10} (x) = 512x ^ {10} -1280x ^ {8} + 1120x ^ {6} -400x ^ {4} + 50x ^ {2} -1 \ T_ {11} (x) = 1024x ^ {11} -2816x ^ {9} + 2816x ^ {7} -1232x ^ {5 } + 220x ^ {3} -11x end {align}}}
Второй вид
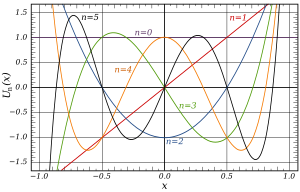
первые несколько полиномов Чебышева второго рода: OEIS : A053117
- U 0 (x) = 1 U 1 (x) = 2 x U 2 (x) = 4 x 2 — 1 U 3 (x) = 8 x 3 — 4 x U 4 (x) = 16 x 4 — 12 x 2 + 1 U 5 (x) = 32 x 5 — 32 x 3 + 6 x U 6 (x) = 64 x 6 — 80 x 4 + 24 x 2 — 1 U 7 (x) = 128 x 7 — 192 x 5 + 80 x 3 — 8 x U 8 (x) = 256 x 8 — 448 x 6 + 240 x 4 — 40 x 2 + 1 U 9 (x) = 512 x 9 — 1024 x 7 + 672 x 5 — 160 x 3 + 10 x { displaystyle { begin {align} U_ {0} (x) = 1 \ U_ {1} (x) = 2x \ U_ {2} (x) = 4x ^ {2} -1 \ U_ {3} (x) = 8x ^ {3} -4x \ U_ { 4} (x) = 16x ^ {4} -12x ^ {2} +1 \ U_ {5} (x) = 32x ^ {5} -32x ^ {3} + 6x \ U_ {6} (x) = 64x ^ {6} -80x ^ {4} + 24x ^ {2} -1 \ U_ {7} (x) = 128x ^ {7} -192x ^ {5} + 80x ^ { 3} -8x \ U_ {8} (x) = 256x ^ {8} -448x ^ {6} + 240x ^ {4} -40x ^ {2} +1 \ U_ {9} (x) = 512x ^ {9} -1024x ^ {7} + 672x ^ {5} -160x ^ {3} + 10x end {align}}}
В качестве базового набора

В соответствующем пространстве Соболева множество полиномов Чебышева образуют ортонормированный базис, так что функция в том же пространстве может быть выражена на −1 ≤ x ≤ 1 через разложение:
- f (x) = ∑ n = 0 ∞ an T n (x). { displaystyle f (x) = sum _ {n = 0} ^ { infty} a_ {n} T_ {n} (x).}
Кроме того, как упоминалось ранее, полиномы Чебышева образуют ортогональный базис, который (среди прочего) подразумевает, что коэффициенты a n могут быть легко определены посредством применения внутреннего произведения. Эта сумма называется рядом Чебышева или разложением Чебышева .
Поскольку ряд Чебышева связан с рядом Фурье по косинусу заменой переменных, все теоремы, тождества и т. д., применимые к ряду Фурье, имеют аналог Чебышева. Эти атрибуты включают:
- Многочлены Чебышева образуют полную ортогональную систему.
- Ряд Чебышева сходится к f (x), если функция кусочно гладкий и непрерывный. Требование гладкости может быть ослаблено в большинстве случаев — до тех пор, пока существует конечное число разрывов в f (x) и ее производных.
- При разрыве ряд сходится к среднему правому и левые пределы.
Обилие теорем и тождеств, унаследованных от ряда Фурье, делает полиномы Чебышева важным инструментом в числовом анализе ; например, они являются наиболее популярными базисными функциями общего назначения, используемыми в спектральном методе, часто в пользу тригонометрических рядов из-за более быстрой сходимости для непрерывных функций (феномен Гиббса все еще остается проблема).
Пример 1
Рассмотрим чебышёвское разложение log (1 + x). Можно выразить
- log (1 + x) = ∑ n = 0 ∞ a n T n (x). { displaystyle log (1 + x) = sum _ {n = 0} ^ { infty} a_ {n} T_ {n} (x) ~.}
Можно найти коэффициенты a n либо посредством применения внутреннего продукта , либо с помощью условия дискретной ортогональности. Для внутреннего произведения
- ∫ — 1 + 1 T m (x) log (1 + x) 1 — x 2 dx = ∑ n = 0 ∞ an ∫ — 1 + 1 T m (x) T n ( x) 1 — x 2 dx, { displaystyle int _ {- 1} ^ {+ 1} , { frac {, T_ {m} (x) , log (1 + x) ,} {, { sqrt {1-x ^ {2} ,}} ,}} , mathrm {d} x = sum _ {n = 0} ^ { infty} a_ {n} int _ {- 1} ^ {+ 1} { frac {T_ {m} (x) , T_ {n} (x)} {, { sqrt {1-x ^ {2} ,}} ,}} , mathrm {d} x ~,}
что дает
- an = {- log 2 для n = 0, — 2 (- 1) nn для n>0. { displaystyle a_ {n} = { begin {cases} — log 2 quad { text {for}} ~ n = 0 ~, \ { frac {, — 2 (-1) ^ { n} ,} {n}} quad { text {for}} ~ n>0 ~. end {ases}}}
В качестве альтернативы, когда внутренний продукт аппроксимируемая функция не может быть вычислена, условие дискретной ортогональности дает часто полезный результат для приближенных коэффициентов,
- an ≈ 2 — δ 0 n N ∑ k = 0 N — 1 T n (xk) log (1 + xk), { displaystyle a_ {n} приблизительно { frac {, 2- delta _ {0n} ,} {N}} , sum _ {k = 0} ^ {N-1} T_ {n } (x_ {k}) , log (1 + x_ {k}) ~,}
где δ ij — дельта-функция Кронекера, а x k — N нулей Гаусса – Чебышева для T N (x):
- xk = cos (π (k + 1 2) N). { displaystyle x_ {k} = cos left (, { frac { pi left (, k + { tfrac {1} {2}} , right)} {N}} , right).}
Для любого N эти приближенные коэффициенты ts обеспечивают точное приближение к функции при x k с контролируемой ошибкой между этими точками. Точные коэффициенты получаются при N = ∞, таким образом представляя функцию точно во всех точках в [−1,1]. Скорость сходимости зависит от функции и ее гладкости.
Это позволяет нам очень эффективно вычислять приблизительные коэффициенты a n с помощью дискретного косинусного преобразования
- an ≈ 2 — δ 0 n N ∑ k = 0 N — 1 соз (п π (k + 1 2) N) журнал (1 + xk). { displaystyle a_ {n} приблизительно { frac {2- delta _ {0n}} {N}} sum _ {k = 0} ^ {N-1} cos left (, { frac {n pi , left (, k + { tfrac {1} {2}} , right)} {N}} , right) log (1 + x_ {k}) ~.}
Пример 2
Другой пример:
- (1 — x 2) α = — 1 π Γ (1 2 + α) Γ (α + 1) + 2 1-2 α ∑ n = 0 (- 1) n (2 α α — n) T 2 n (x) = 2-2 α ∑ n = 0 (- 1) n (2 α + 1 α — n) U 2 n (x). { displaystyle { begin {align} (1-x ^ {2}) ^ { alpha} ~ = ~ — { frac {1} {, { sqrt { pi ,}} ,} } , { frac {, Gamma left (, { tfrac {1} {2}} + alpha , right) ,} { Gamma (, alpha +1 ,) }} + 2 ^ {1-2 alpha} , sum _ {n = 0} (- 1) ^ {n} , {2 alpha choose alpha -n} , T_ {2n} ( x) \ ~ = ~ 2 ^ {- 2 alpha} , sum _ {n = 0} (- 1) ^ {n} , {2 alpha +1 choose alpha -n} , U_ {2n} (x) ~. End {align}}}
Частичные суммы
Частичные суммы
- f (x) = ∑ n = 0 ∞ an T n (x) { displaystyle f (x) = sum _ {n = 0} ^ { infty} a_ {n} T_ {n} (x)}
очень полезны в приближении различные функции и в решении дифференциальных уравнений (см. спектральный метод ). Два общих метода определения коэффициентов a n — это использование внутреннего произведения, как в метод Галеркина, и использование коллокации, который связан с интерполяцией.
В качестве интерполянта N коэффициентов (N — 1) -й частичной суммы обычно получают на точках Чебышева – Гаусса – Лобатто (или сетке Лобатто), что приводит к ошибка и позволяет избежать явления Рунге, связанного с однородной сеткой. Этот набор точек соответствует экстремумам полинома наивысшего порядка в сумме плюс конечные точки и определяется выражением:
- x k = — cos (k π N — 1); k = 0, 1,…, N — 1. { Displaystyle х_ {к} = — соз влево (, { гидроразрыва {, к пи ,} {, N-1 ,}} , вправо) ,; qquad k = 0,1, dots, N-1 ~.}
Многочлен в форме Чебышева
Произвольный многочлен степени N можно записать через многочлены Чебышева первого рода. Такой многочлен p (x) имеет вид
- p (x) = ∑ n = 0 N a n T n (x). { displaystyle p (x) = sum _ {n = 0} ^ {N} a_ {n} T_ {n} (x) ~.}
Многочлены в форме Чебышева можно вычислить с помощью Clenshaw алгоритм.
Сдвинутые многочлены Чебышева
Сдвинутые многочлены Чебышева первого рода определяются как
- T n ∗ (x) = T n (2 x — 1). { displaystyle T_ {n} ^ {*} (x) = T_ {n} (2x-1) ~.}
Когда аргумент полинома Чебышева находится в диапазоне 2x — 1 ∈ [−1, 1] аргумент сдвинутого многочлена Чебышева равен x ∈ [0, 1]. Точно так же можно определить сдвинутые многочлены для общих интервалов [a, b].
Многочлены распространения
Полиномы распространения представляют собой изменение масштаба сдвинутых многочленов Чебышева первого рода, так что диапазон также равен [0, 1]. То есть
- S n (x) = 1 — T n (1-2 x) 2. { displaystyle S_ {n} (x) = { frac {, 1-T_ {n} (1-2x) ,} {2}} ~.}
См. также
Литература
Источники
- Абрамовиц, Милтон ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 22». Справочник по математическим функциям с формулами, графиками и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Dette, Holger (1995). «Заметка о некоторых своеобразных нелинейных экстремальных явлениях полиномов Чебышева». Труды Эдинбургского математического общества. 38 (2): 343–355. arXiv : математика / 9406222. doi : 10.1017 / S001309150001912X. S2CID 16703489.
- Эллиотт, Дэвид (1964). «Оценка и оценка коэффициентов в разложении функции в ряд Чебышева». Математика. Комп. 18 (86): 274–284. doi : 10.1090 / S0025-5718-1964-0166903-7. MR 0166903.
- Еременко А.; Лемперт, Л. (1994). «Экстремальная задача для многочленов» (PDF). Труды Американского математического общества. 122 (1): 191–193. doi : 10.1090 / S0002-9939-1994-1207536-1. MR 1207536.
- Эрнандес, М.А. (2001). «Чебышевские аппроксимационные алгоритмы и приложения». Комп. Математика. Applic. 41 (3–4): 433–445. doi : 10.1016 / s0898-1221 (00) 00286-8.
- Мейсон, Дж. К. (1984). «Некоторые свойства и приложения полинома Чебышева и рациональной аппроксимации». Рациональная аппроксимация и интерполяция. Конспект лекций по математике. 1105 . С. 27–48. doi : 10.1007 / BFb0072398. ISBN 978-3-540-13899-0.
- Mason, J.C.; Хэндскомб, округ Колумбия (2002). Полиномы Чебышева. Тейлор и Фрэнсис.
- Матар, Р. Дж. (2006). «Разложение обратных многочленов в ряд Чебышева». J. Comput. Appl. Математика. 196 (2): 596–607. arXiv : математика / 0403344. Bibcode : 2006JCoAM.196..596M. doi : 10.1016 / j.cam.2005.10.013. S2CID 16476052.
- Koornwinder, Tom H.; Wong, Roderick S.C.; Коэкоек, Рулоф; Сварттоу, Рене Ф. (2010), «Ортогональные многочлены», в Олвер, Фрэнк У. Дж. ; Lozier, Daniel M.; Boisvert, Рональд Ф.; Кларк, Чарльз У. (ред.), Справочник по математическим функциям NIST, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
- Ремес, Юджин. «Об одном экстремальном свойстве многочленов Чебышева» (PDF).
- Зальцер, Герберт Э. (1976). «Преобразование интерполяционного ряда в ряд Чебышева по рекуррентным формулам». Математика. Комп. 30 (134): 295–302. doi : 10.1090 / S0025-5718-1976-0395159-3. MR 0395159.
- Скрэтон, Р.Э. (1969). «Решение интегральных уравнений в ряду Чебышева». Математика. Comput. 23 (108): 837–844. doi : 10.1090 / S0025-5718-1969-0260224-4. MR 0260224.
- Смит, Лайл Б. (1966). «Вычисление коэффициентов ряда Чебышева». Comm. ACM. 9 (2): 86–87. doi : 10.1145 / 365170.365195. S2CID 8876563. Алгоритм 277.
- Суетин, П.К. (2001) [1994], Математическая энциклопедия, EMS Press
Внешние ссылки
- Вайсштейн, Эрик У. «Многочлены Чебышева первого рода». MathWorld.
- Мэтьюз, Джон Х. (2003). «Модуль для полиномов Чебышева». Кафедра математики. Примечания к курсу математики 340 Численный анализ и математика 440 Расширенный численный анализ. Фуллертон, Калифорния: Университет штата Калифорния. Архивировано из оригинала 29 мая 2007 г. Дата обращения 17 августа 2020 г.
- «Чебышевская интерполяция: интерактивный тур». Математическая ассоциация Америки (MAA) — включает иллюстративный Java-апплет.
- «Численные вычисления с функциями». Проект Chebfun.
- «Есть ли интуитивное объяснение экстремального свойства полиномов Чебышева?». Математическое переполнение. Вопрос 25534.
- «Полиномиальное вычисление Чебышева и преобразование Чебышева». Увеличение. Математика.
Эти многочлены Чебышева две последовательности многочленов , связанных с косинус и синус функций, нотных , как и . Их можно определить несколькими способами, которые имеют одинаковый конечный результат; В этой статье полиномы определяются, начиная с тригонометрических функций :
- В полиномы Чебышева первого рода задаются
- Аналогичным образом определим полиномы Чебышева второго рода как
Эти определения не кажутся полиномами , но с помощью различных тригонометрических тождеств их можно преобразовать в явно полиномиальную форму. Например, при п = 2 , Т 2 формула может быть преобразована в многочлен с аргументом х = соз ( & thetas ) , используя формулу двойного угла:
Заменяя термины в формуле на определения выше, мы получаем
Остальные T n ( x ) определяются аналогично, где для многочленов второго рода ( U n ) мы должны использовать формулу де Муавра, чтобы получить sin ( n θ ) как sin ( θ ), умноженный на многочлен от cos ( θ ) . Например,
дает
После преобразования в полиномиальную форму T n ( x ) и U n ( x ) называются полиномами Чебышева первого и второго рода соответственно.
И наоборот, произвольная целая степень тригонометрических функций может быть выражена как линейная комбинация тригонометрических функций с использованием полиномов Чебышева.
где штрих у символа суммы указывает, что вклад j = 0 необходимо уменьшить вдвое, если он появляется, и .
Важным и удобным свойством T n ( x ) является то, что они ортогональны относительно внутреннего произведения
и U n ( x ) ортогональны по отношению к другому аналогичному внутреннему произведению , указанному ниже. Это следует из того, что полиномы Чебышева решают дифференциальные уравнения Чебышева
которые являются дифференциальными уравнениями Штурма – Лиувилля . Общей чертой таких дифференциальных уравнений является выделенный ортонормированный набор решений. (Другой способ определить полиномы Чебышева — это решения этих уравнений .)
Многочлены Чебышева T n — это многочлены с максимально возможным старшим коэффициентом, модуль которого на интервале [−1, 1] ограничен числом 1. Они также являются «экстремальными» многочленами для многих других свойств.
Многочлены Чебышева важны в теории приближений, потому что корни T n ( x ) , которые также называются узлами Чебышева , используются в качестве точек согласования для оптимизации полиномиальной интерполяции . Результирующий полином интерполяции минимизирует проблему явления Рунге и обеспечивает приближение, близкое к наилучшему полиномиальному приближению непрерывной функции при максимальной норме , также называемое критерием « минимакс ». Это приближение непосредственно приводит к методу квадратур Кленшоу – Кертиса .
Эти многочлены были названы в честь Пафнутия Чебышева . Буква T используется из-за альтернативных транслитераций имени Чебышев как Чебышев , Чебышев (французский язык) или Tschebyschow (немецкий язык).
Определения
Определение повторения
График первых пяти T n многочленов Чебышева первого рода
Эти многочлены Чебышева первого рода получается из рекуррентного соотношения
Обыкновенная производящая функция для Т п является
Есть несколько других производящих функций для многочленов Чебышева; экспоненциальная производящая функция является
Производящая функция, имеющая отношение к теории двумерного потенциала и мультипольному разложению, имеет вид
Сюжет из первых пяти U п многочленов Чебышева второго рода
Эти многочлены Чебышева второго рода определяются рекуррентным соотношением
Обратите внимание , что два набора рекуррентных соотношений идентичны, за исключением VS. .
Обычная производящая функция для U n есть
экспоненциальная производящая функция
Тригонометрическое определение
Как описано во введении, многочлены Чебышева первого рода можно определить как единственные многочлены, удовлетворяющие
или, другими словами, как единственные многочлены, удовлетворяющие
для n = 0, 1, 2, 3,… что с технической точки зрения является вариантом (эквивалентным транспонированием) уравнения Шредера . То есть, T n ( x ) функционально сопряжен с nx , кодифицированным в свойстве вложенности ниже.
Полиномы второго рода удовлетворяют:
или
которое структурно очень похоже на ядро Дирихле D n ( x ) :
То, что cos nx является многочленом n- й степени от cos x, можно увидеть, заметив, что cos nx является действительной частью одной стороны формулы де Муавра . Действительная часть другой стороны является многочленом от cos x и sin x , в котором все степени sin x четны и, таким образом, заменяются тождеством cos 2 x + sin 2 x = 1 . По тем же соображениям sin nx является мнимой частью многочлена, в котором все степени sin x нечетны, и, таким образом, если исключить одну, оставшуюся можно заменить, чтобы создать многочлен ( n — 1) -й степени в cos x .
Это тождество весьма полезно в сочетании с рекурсивной формулой генерации, поскольку оно позволяет вычислить косинус любого целого кратного угла исключительно в терминах косинуса основного угла.
Вычисляя первые два полинома Чебышева,
а также
можно прямо определить, что
и так далее.
Два непосредственных следствия — это идентичность композиции (или свойство вложенности, определяющее полугруппу )
и выражение комплексного возведения в степень через полиномы Чебышева: при z = a + bi ,
Определение уравнения Пелла
Многочлены Чебышева также можно определить как решения уравнения Пелля
в кольце R [ x ] . Таким образом, они могут быть сгенерированы стандартной техникой для уравнений Пелла взятия степеней фундаментального решения:
Связь между двумя видами многочленов Чебышева
Полиномы Чебышева первого и второго рода соответствуют дополнительной паре последовательностей Люка Ṽ n ( P , Q ) и Ũ n ( P , Q ) с параметрами P = 2 x и Q = 1 :
Отсюда следует, что они также удовлетворяют паре уравнений взаимной рекуррентности:
Многочлены Чебышева первого и второго рода также связаны следующими соотношениями:
Рекуррентное соотношение производной полиномов Чебышева может быть получено из этих соотношений:
Это соотношение используется в спектральном методе Чебышева решения дифференциальных уравнений.
Неравенства Турана для полиномов Чебышева имеют вид
Интегральные отношения:
где интегралы считаются главным значением.
Явные выражения
Различные подходы к определению полиномов Чебышева приводят к различным явным выражениям, таким как:
с обратным
где штрих у символа суммы указывает, что вклад j = 0 необходимо уменьшить вдвое, если он появляется.
где 2 F 1 — гипергеометрическая функция .
Характеристики
Симметрия
То есть полиномы Чебышева четного порядка имеют четную симметрию и содержат только четные степени x . Многочлены Чебышева нечетного порядка обладают нечетной симметрией и содержат только нечетные степени x .
Корни и экстремумы
Многочлен Чебышева любого вида со степенью n имеет n различных простых корней, называемых корнями Чебышева , в интервале [−1, 1] . Корни полинома Чебышева первого рода иногда называют узлами Чебышева, потому что они используются как узлы при полиномиальной интерполяции. Используя тригонометрическое определение и тот факт, что
можно показать, что корни T n равны
Точно так же корни U n равны
Экстремумы из Т п на отрезке -1 ≤ х ≤ 1 расположены на
Одно уникальное свойство многочленов Чебышева первого рода состоит в том, что на интервале −1 ≤ x ≤ 1 все экстремумы имеют значения либо −1, либо 1. Таким образом, эти многочлены имеют только два конечных критических значения , определяющее свойство Многочлены Шабата . И первый, и второй виды многочлена Чебышева имеют экстремумы на концах, определяемые выражением:
Дифференциация и интеграция
Производные многочленов могут быть не такими простыми. Дифференцируя полиномы в их тригонометрической форме, можно показать, что:
Последние две формулы могут быть затруднительны в числовом отношении из-за деления на ноль (0/0 неопределенная форма , в частности) при x = 1 и x = −1 . Можно показать, что:
|
Доказательство |
|---|
|
Вторая производная полинома Чебышева первого рода равна который, если оценивать, как показано выше, создает проблему, потому что он неопределен при x = ± 1 . Поскольку функция является полиномом, (все) производные должны существовать для всех действительных чисел, поэтому ограничение приведенного выше выражения должно дать желаемое значение: где пока рассматривается только x = 1 . Фактор знаменателя: Поскольку предел в целом должен существовать, предел числителя и знаменателя должны существовать независимо, и Знаменатель (по-прежнему) ограничивается нулем, что означает, что числитель должен ограничиваться нулем, то есть U n — 1 (1) = nT n (1) = n, что будет полезно в дальнейшем. Поскольку числитель и знаменатель ограничиваются нулем, применяется правило L’Hôpital : Доказательство для x = −1 аналогично, но важно то, что T n (−1) = (−1) n . |
Более общая формула гласит:
что очень полезно при численном решении задач на собственные значения.
Также у нас есть
где штрих у символов суммирования означает, что член, вносимый k = 0 , должен быть уменьшен вдвое, если он появляется.
Что касается интегрирования, первая производная от T n означает, что
а рекуррентное соотношение для многочленов первого рода, содержащих производные, устанавливает, что при n ≥ 2
Последней формулой можно дополнительно манипулировать, чтобы выразить интеграл от T n как функцию многочленов Чебышева только первого рода:
Кроме того, у нас есть
Произведения полиномов Чебышева
При работе с многочленами Чебышева довольно часто встречаются произведения двух из них. Эти произведения могут быть сведены к комбинациям полиномов Чебышева с более низкой или более высокой степенью, и заключительные утверждения о продукте сделать легче. Предполагается, что в дальнейшем индекс m больше или равен индексу n и n не является отрицательным. Для многочленов Чебышева первого рода произведение разлагается до
что является аналогом теоремы сложения
с идентичностями
Для n = 1 это приводит к уже известной рекуррентной формуле, только расположенной по-другому, а при n = 2 она образует рекуррентное соотношение для всех четных или всех нечетных многочленов Чебышева (в зависимости от четности наименьшего m ), что позволяет проектировать функции с заданными свойствами симметрии. Из этого разложения в произведение можно заключить еще три полезные формулы для вычисления полиномов Чебышева:
Для полиномов Чебышева второго рода произведения можно записать в виде:
для m ≥ n .
Таким образом, как и выше, при n = 2 рекуррентная формула для многочленов Чебышева второго рода сводится для обоих типов симметрии к
в зависимости от того, начинается ли m с 2 или 3.
Ортогональность
И T n, и U n образуют последовательность ортогональных многочленов . Полиномы первого рода T n ортогональны относительно веса
на интервале [−1, 1] , т.е. имеем:
Это можно доказать, положив x = cos θ и используя определяющее тождество T n (cos θ ) = cos nθ .
Аналогично полиномы второго рода U n ортогональны относительно веса
на интервале [−1, 1] , т.е. имеем:
(Мера √ 1 — x 2 d x с точностью до нормирующей константы является полукруглым распределением Вигнера .)
Т п удовлетворяет также дискретное условие ортогональности:
где N — любое целое число больше max ( i , j ) , а x k — это N чебышёвских узлов (см. выше) T N ( x ) :
Для многочленов второго рода и любого целого числа N > i + j с одинаковыми чебышевскими узлами x k существуют аналогичные суммы:
и без весовой функции:
Для любого целого числа N > i + j на основе N нулей U N ( x ) :
можно получить сумму:
и снова без весовой функции:
Минимальная ∞ -норма
Для любого заданного n ≥ 1 среди многочленов степени n со старшим коэффициентом 1 ( монические многочлены)
это тот, у которого максимальное абсолютное значение на интервале [−1, 1] минимально.
Это максимальное абсолютное значение равно
и | f ( x ) | достигает этого максимума ровно n + 1 раз при
|
Доказательство |
|---|
|
Предположим, что w n ( x ) — многочлен степени n со старшим коэффициентом 1 с максимальным модулем на интервале [−1,1] меньше 1/2 n — 1 . Определять Поскольку в крайних точках T n имеем Из теоремы промежуточного значения , е п ( х ) имеет по крайней мере п корней. Однако это невозможно, поскольку f n ( x ) является многочленом степени n — 1 , поэтому из фундаментальной теоремы алгебры следует, что у него не более n — 1 корней. |
- Замечание
По теореме об эквивалентных колебаниях среди всех многочленов степени ≤ n многочлен f минимизирует || f || ∞ на [−1,1] тогда и только тогда, когда существует n + 2 точек −1 ≤ x 0 < x 1 <⋯ < x n + 1 ≤ 1 таких, что | f ( x i ) | = || f || ∞ .
Конечно, нулевой многочлен на интервале [−1,1] может быть найден сам по себе и минимизирует ∞ -норму.
Однако выше | f | достигает своего максимума только n + 1 раз, потому что мы ищем лучший многочлен степени n ≥ 1 (поэтому приведенная ранее теорема не может быть использована).
Прочие свойства
Полиномы Чебышева являются частным случаем ультрасферических полиномов или полиномов Гегенбауэра , которые сами по себе являются частным случаем полиномов Якоби :
Для любого неотрицательного целого числа n , T n ( x ) и U n ( x ) являются полиномами степени n . Они являются четными или нечетными функциями от х , как п четного или нечетным, так что, когда записываются в виде многочленов от х , он имеет только четные или нечетные степени терминов соответственно. По факту,
а также
Старший коэффициент T n равен 2 n — 1, если 1 ≤ n , и 1, если 0 = n .
T n — это частный случай кривых Лиссажу с отношением частот, равным n .
Несколько полиномиальных последовательностей, таких как многочлены Люка ( L n ), многочлены Диксона ( D n ), многочлены Фибоначчи ( F n ), связаны с многочленами Чебышева T n и U n .
Многочлены Чебышева первого рода удовлетворяют соотношению
что легко доказывается из формулы произведения на сумму косинуса. Полиномы второго рода удовлетворяют аналогичному соотношению
(с определением U −1 ≡ 0 по соглашению).
Аналогично формуле
у нас есть аналогичная формула
Для й ≠ 0 ,
а также
что следует из того, что это верно по определению при x = e iθ .
Определять
Тогда C n ( x ) и C m ( x ) — коммутирующие многочлены:
как это видно в абелевой вложенности имущества , указанного выше.
Обобщенные полиномы Чебышева
Обобщенные многочлены Чебышева T a определяются равенством
где a не обязательно является целым числом, а 2 F 1 ( a , b ; c ; z ) — гипергеометрическая функция Гаусса ; в качестве примера . Расширение степенного ряда
сходится для .![x in [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)
Примеры
Первый вид
Первые несколько полиномов Чебышева первого рода в области −1 < x <1 : плоские T 0 , T 1 , T 2 , T 3 , T 4 и T 5 .
Первые несколько полиномов Чебышева первого рода — это OEIS : A028297
Второй вид
Первые несколько полиномов Чебышева второго рода в области −1 < x <1 : плоские U 0 , U 1 , U 2 , U 3 , U 4 и U 5 . Хотя это не видно на изображении, U n (1) = n + 1 и U n (−1) = ( n + 1) (- 1) n .
Первые несколько полиномов Чебышева второго рода — это OEIS : A053117
В качестве базового набора
Негладкая функция (вверху) y = — x 3 H (- x ) , где H — ступенчатая функция Хевисайда , и (внизу) 5-я частичная сумма ее разложения Чебышёва. 7-я сумма неотличима от исходной функции при разрешении графика.
В соответствующем пространстве Соболева набор многочленов Чебышева образует ортонормированный базис , так что функция в том же пространстве может быть выражена на −1 ≤ x ≤ 1 через разложение:
Кроме того, как упоминалось ранее, полиномы Чебышева образуют ортогональный базис, который (среди прочего) подразумевает, что коэффициенты a n могут быть легко определены посредством применения внутреннего произведения . Эта сумма называется чебышёвским рядом или чебышёвским разложением .
Поскольку ряд Чебышева связан с рядом косинусов Фурье заменой переменных, все теоремы, тождества и т. Д., Применимые к рядам Фурье, имеют аналог Чебышева. Эти атрибуты включают:
- Многочлены Чебышева образуют полную ортогональную систему.
- Ряд Чебышева сходится к f ( x ), если функция кусочно гладкая и непрерывная . Требование гладкости может быть ослаблено в большинстве случаев — до тех пор, пока существует конечное число разрывов в f ( x ) и ее производных.
- На разрыве ряд сходится к среднему значению правого и левого пределов.
Обилие теорем и тождеств, унаследованных от рядов Фурье, делает полиномы Чебышева важным инструментом численного анализа ; например, они являются наиболее популярными базисными функциями общего назначения, используемыми в спектральном методе , часто в пользу тригонометрических рядов из-за, как правило, более быстрой сходимости для непрерывных функций ( феномен Гиббса все еще остается проблемой).
Пример 1
Рассмотрим чебышёвское разложение log (1 + x ) . Можно выразить
Коэффициенты a n можно найти либо с помощью внутреннего продукта, либо с помощью условия дискретной ортогональности. Для внутреннего продукта
который дает
В качестве альтернативы, когда внутренний продукт аппроксимируемой функции не может быть оценен, условие дискретной ортогональности дает часто полезный результат для приближенных коэффициентов,
где δ ij — дельта- функция Кронекера, а x k — N нулей Гаусса – Чебышева T N ( x ) :
Для любого N эти приблизительные коэффициенты обеспечивают точное приближение к функции в точке x k с контролируемой ошибкой между этими точками. Точные коэффициенты получаются при N = ∞ , таким образом представляя функцию точно во всех точках в [−1,1] . Скорость сходимости зависит от функции и ее гладкости.
Это позволяет нам очень эффективно вычислять приблизительные коэффициенты a n с помощью дискретного косинусного преобразования
Пример 2
Другой пример:
Частичные суммы
Частичные суммы
очень полезны при приближении различных функций и при решении дифференциальных уравнений (см. спектральный метод ). Два общих метода определения коэффициентов a n — это использование внутреннего произведения, как в методе Галеркина, и использование коллокации, которая связана с интерполяцией .
В качестве интерполянта N коэффициентов ( N — 1) -й частичной суммы обычно получают на точках Чебышева – Гаусса – Лобатто (или сетке Лобатто), что дает минимальную ошибку и позволяет избежать явления Рунге, связанного с однородной сеткой. Этот набор точек соответствует экстремумам полинома наивысшего порядка в сумме плюс конечные точки и задается следующим образом:
Многочлен в форме Чебышева
Произвольный многочлен степени N можно записать через многочлены Чебышева первого рода. Такой многочлен p ( x ) имеет вид
Многочлены в форме Чебышева можно вычислить с помощью алгоритма Кленшоу .
Сдвинутые многочлены Чебышева
Сдвинутые полиномы Чебышева первого рода определяются как
Когда аргумент многочлена Чебышева находится в диапазоне 2 x — 1 ∈ [−1, 1], аргумент сдвинутого многочлена Чебышева равен x ∈ [0, 1] . Точно так же можно определить сдвинутые многочлены для общих интервалов [ a , b ] .
Смотрите также
- Фильтр Чебышева
- Кубический корень Чебышева
- Полиномы Диксона
- Полиномы Лежандра
- Полиномы Эрмита
- Минимальный многочлен от 2cos (2pi / n)
- Полиномы Романовского
- Чебышёвские рациональные функции
- Теория приближений
- Система Chebfun
- Дискретное преобразование Чебышева
- Неравенство братьев Марковых
использованная литература
Источники
- Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964]. «Глава 22» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 773. ISBN. 978-0-486-61272-0. LCCN 64-60036 . Руководство по ремонту 0167642 . LCCN 65-12253 .
- Детте, Хольгер (1995). «Заметка о некоторых своеобразных нелинейных экстремальных явлениях полиномов Чебышева». Труды Эдинбургского математического общества . 38 (2): 343–355. arXiv : math / 9406222 . DOI : 10.1017 / S001309150001912X . S2CID 16703489 .
- Эллиотт, Дэвид (1964). «Вычисление и оценка коэффициентов разложения функции в ряд Чебышева» . Математика. Комп . 18 (86): 274–284. DOI : 10.1090 / S0025-5718-1964-0166903-7 . Руководство по ремонту 0166903 .
- Еременко, А .; Лемперт, Л. (1994). «Экстремальная задача для многочленов» (PDF) . Труды Американского математического общества . 122 (1): 191–193. DOI : 10.1090 / S0002-9939-1994-1207536-1 . Руководство по ремонту 1207536 .
- Эрнандес, Массачусетс (2001). «Чебышевские аппроксимационные алгоритмы и приложения» . Комп. Математика. Applic . 41 (3–4): 433–445. DOI : 10.1016 / s0898-1221 (00) 00286-8 .
- Мейсон, JC (1984). «Некоторые свойства и приложения полинома Чебышева и рациональной аппроксимации». Рациональная аппроксимация и интерполяция . Конспект лекций по математике. 1105 . С. 27–48. DOI : 10.1007 / BFb0072398 . ISBN 978-3-540-13899-0.
- Мейсон, JC; Хэндскомб, округ Колумбия (2002). Полиномы Чебышева . Тейлор и Фрэнсис.
- Матар, RJ (2006). «Разложение обратных многочленов в ряд Чебышева». J. Comput. Прил. Математика . 196 (2): 596–607. arXiv : math / 0403344 . Bibcode : 2006JCoAM.196..596M . DOI : 10.1016 / j.cam.2005.10.013 . S2CID 16476052 .
- Koornwinder, Tom H .; Wong, Roderick SC; Коэкоек, Рулоф; Свартту, Рене Ф. (2010), «Ортогональные многочлены» , в Olver, Frank WJ ; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник по математическим функциям NIST , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
- Ремес, Евгений. «Об одном экстремальном свойстве многочленов Чебышева» (PDF) .
- Зальцер, Герберт Э. (1976). «Преобразование интерполяционных рядов в ряды Чебышева по рекуррентным формулам» . Математика. Комп . 30 (134): 295–302. DOI : 10.1090 / S0025-5718-1976-0395159-3 . Руководство по ремонту 0395159 .
- Scraton, RE (1969). «Решение интегральных уравнений в рядах Чебышева» . Математика. Comput . 23 (108): 837–844. DOI : 10.1090 / S0025-5718-1969-0260224-4 . Руководство по ремонту 0260224 .
- Смит, Лайл Б. (1966). «Вычисление коэффициентов ряда Чебышева». Comm. ACM . 9 (2): 86–87. DOI : 10.1145 / 365170.365195 . S2CID 8876563 . Алгоритм 277.
- Суетин, П.К. (2001) [1994], «Многочлены Чебышева» , Энциклопедия математики , EMS Press
внешние ссылки
-
СМИ, связанные с полиномами Чебышева, на Викискладе?
- Вайсштейн, Эрик В. «Многочлены Чебышева первого рода» . MathWorld .
- Мэтьюз, Джон Х. (2003). «Модуль для полиномов Чебышева» . Кафедра математики. Примечания к курсу математики 340 Численный анализ и математика 440 Расширенный численный анализ . Фуллертон, Калифорния: Университет штата Калифорния. Архивировано из оригинального 29 мая 2007 года . Проверено 17 августа 2020 .
- «Чебышевская интерполяция: интерактивный тур» . Математическая ассоциация Америки (MAA)— включает иллюстративный Java-апплет .
- «Численные вычисления с функциями» . Проект Chebfun .
- «Есть ли интуитивное объяснение экстремального свойства многочленов Чебышева?» . Математическое переполнение . Вопрос 25534.
- «Полиномиальное вычисление Чебышева и преобразование Чебышева» . Boost . Математика.
































































































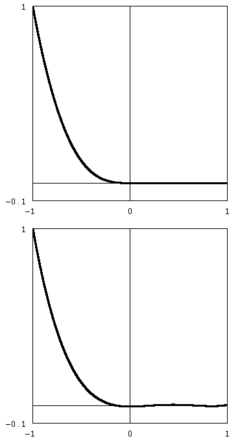





























































































![{ displaystyle x in [ -1,1] ~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10c64188a051d2a599b143d5443e7100f60675d0)





























































