Уравнение и его корни: определения, примеры
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня — 2 , 1 и 5 , то пишем — 2 , 1 , 5 или < — 2 , 1 , 5 >.
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
-
Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
-
Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
-
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Что такое уравнение и корни уравнения? Как решить уравнение?
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x= 2x -5
4+3x -2x =-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4 +3x-2x=-5
3x-2x=-5 -4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅ (-9) =2⋅ (-9) -5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
Далее делим все уравнение на 3.
3x :3 =45 :3
(3:3)x=15
Сделаем проверку. Подставим в уравнение найденный корень.
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
http://tutomath.ru/6-klass/chto-takoe-uravnenie-i-korni-uravneniya-kak-reshit-uravnenie.html
Корень алгебраического уравнения
- Корень алгебраического уравнения
-
Корень многочлена
над полем k — элемент
, который после подстановки его вместо x обращает уравнение
в тождество.
Свойства
- Если c является корнем многочлена p(x), то p(x) делится без остатка на x − c (теорема Безу).
- Число вещественных корней многочлена с вещественными коэффициентами степени n заведомо меньше либо равно n. При этом комплексные корни многочлена (если они есть) сопряжены, таким образом, многочлен четной степени может иметь только четное число вещественных корней, а многочлен нечётной — только нечётное.
- Всякий многочлен p(x) с вещественными или комплексными коэффициентами имеет по крайней мере один, вообще говоря, комплексный, корень (основная теорема алгебры).
- Аналогичное утверждение верно для любого алгебраически замкнутого поля.
- Более того, многочлен с вещественными коэффициентами p(x) можно записать в виде
-
- где
— (в общем случае комплексные) корни многочлена p(x), возможно с повторениями, при этом если среди корней
многочлена p(x) встречаются равные, то общее их значение называется кратным корнем.
- Корни многочлена связаны с его коэффициентами формулами Виета.
Нахождение корней
Способ нахождения корней линейных и квадратичных многочленов, то есть способ решения линейных и квадратных уравнений, был известен ещё в древнем мире. Поиски формулы для точного решения общего уравнения третьей степени продолжались долгое время (следует упомянуть метод, предложенный Омаром Хайямом), пока не увенчались успехом в первой половине XVI века в трудах Сципиона дель Ферро, Никколо Тарталья и Джероламо Кардано. Формулы для корней квадратных и кубических уравнений позволили сравнительно легко получить формулы для корней уравнения четвертой степени.
То, что корни общего уравнения пятой степени и выше не выражаются при помощи рациональных функций и радикалов от коэффициентов было доказано норвежским математиком Нильсом Абелем в 1826 г. Это совсем не означает, что корни такого уравнения не могут быть найдены. Во-первых, в частных случаях, при некоторых комбинациях коэффициентов корни уравнения при некоторой изобретательности могут быть определены. Во-вторых, существуют формулы для корней уравнений 5-й степени и выше, использующие, однако, специальные функции — эллиптические или гипергеометрические (см., к примеру, корень Бринга).
В случае, если все коэффициенты многочлена рациональны, то нахождение его корней приводится к нахождению корней многочлена с целыми коэффициентами. Для рациональных корней таких многочленов существуют алгоритмы нахождения перебором кандидатов с использованием схемы Горнера, причем при нахождении целых корней перебор может быть существенно уменьшен приемом чистки корней. Также в этом случае можно использовать полиномиальный LLL-алгоритм.
Для приблизительного нахождения (с любой требуемой точностью) вещественных корней многочлена с вещественными коэффициентами используются итерационные методы, например, метод секущих, метод бисекции, метод Ньютона. Количество вещественных корней многочлена на интервале может быть оценено при помощи теоремы Штурма.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Корень алгебраического уравнения» в других словарях:
-
КРАТНЫЙ КОРЕНЬ алгебраического — уравнения такое число b, что f(х) делится без остатка на 2 ю или более высокую степень m двучлена (х b); число m кратность корня b … Большой Энциклопедический словарь
-
Корень (в математике) — Корень в математике, 1) К. степени n из числа а ≈ число х (обозначаемое ), n я степень которого равна а (то есть xn = а). Действие нахождения К. называют извлечением корня. При а ¹ 0 существует n различных значений К. (вообще говоря,… … Большая советская энциклопедия
-
Корень — I Корень (radix) один из основных вегетативных органов листостебельных растений (за исключением мхов), служащий для прикрепления к субстрату, поглощения из него воды и питательных веществ, первичного превращения ряда поглощаемых веществ,… … Большая советская энциклопедия
-
КОРЕНЬ — 1) К. степени n из числа a число n я степень х п к рого равна а. 2) К. алгебраического уравнения над полем К элемент к рый после подстановки его вместо хобращает уравнение в тождество. К. этого уравнения наз. также и К. многочлена Если сявляется… … Математическая энциклопедия
-
Уравнения математической физики — дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории У. м. ф.… … Большая советская энциклопедия
-
кратный корень — алгебраического уравнения f(х) = а0хn + a1xn 1 + … + an = 0, такое число b, что f(х) делится без остатка на 2 ю или более высокую степень m двучлена (х b); число m кратность корня b. * * * КРАТНЫЙ КОРЕНЬ КРАТНЫЙ КОРЕНЬ алгебраического… … Энциклопедический словарь
-
Квадратура круга — Так называется знаменитая задача: построить квадрат, равновеликий по площади кругу данного радиуса. Эта задача была предметом непрерывного ряда усиленных изысканий греческих математиков и значительно повлияла на поразительные успехи геометрии в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Квадратура круга — задача о разыскании квадрата, равновеликого данному кругу. Под К. к. понимают как задачу точного построения квадрата, равновеликого кругу, так и задачу вычисления площади круга с тем или иным приближением. Задачу о точной К. к. пытались… … Большая советская энциклопедия
-
Группа Галуа — Группа Галуа алгебраическая группа, ассоциированная с расширением поля. Играет важную роль при исследовании расширений полей, в частности, в теории Галуа. Это понятие ввёл в математику Эварист Галуа в 1832 году. Содержание 1 Определение 2… … Википедия
-
Алгебра — Общие сведения Алгебра один из больших разделов математики (См. Математика), принадлежащий наряду с арифметикой (См. Арифметика) и геометрией (См. Геометрия) к числу старейших ветвей этой науки. Задачи, а также методы А.,… … Большая советская энциклопедия
Уравнение и его корни: определения, примеры
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня — 2 , 1 и 5 , то пишем — 2 , 1 , 5 или < — 2 , 1 , 5 >.
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Уравнение и его корни
п.1. Определение уравнения и его корня
Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.
Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).
Например, для уравнения 15x+8=23 корнем является значение x=1.
В уравнении x(x + 5)(x — 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$.
Уравнение $x^2 = -1$ действительных корней не имеет.
В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x in Bbb R$, т.е. является тождеством.
Решить уравнение означает найти все его корни или доказать, что их нет.
п.2. Примеры
Пример 1. Решите уравнение и выполните проверку x — (3 — 2x) = 9
x-(3-2x)=9 $iff$ x-3+2x=9 $iff$ x+2x=9+3 $iff$ 3x=12 $iff$ x=4
$4 -(3 — 2 cdot 4)=9 implies 4 — 3 + 8 = 9 implies 9 equiv 9$
Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56
7(x + 3)=56 |:7 $iff$ x + 3 = 8 $iff$ x = 8 — 3 $iff$ x=5
$7(5 + 3) = 56 implies 7 cdot 8 = 56 implies 56 equiv 56$
Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14
(3x + 4) : 2=14 |$times$2 $iff$ 3x + 4 = 28 $iff$ 3x = 28 — 4 $iff$ 3x = 24 $iff$ x=8
$(3 cdot 8 + 4) : 2 = 14 implies (24 + 4) : 2 = 14 implies 28 : 2 = 14 implies 14 equiv 14$
Пример 4. Решите уравнение $ frac<3x-7> <3>— frac <5x-11> <5>= 0$
$frac <3x-7> <3>— frac <5x-11> <5>= 0 | times 15 iff5(3x-7)-3(5x-11)=0 iff$
$ iff 15x-35-15x+33=0 iff 0x=2 iff x in varnothing $
Ответ: $x in varnothing $
Пример 5. Решите уравнение $frac <2x — 7> <2>= frac <3x+6><3>$
$frac <2x-7><2>=frac <3>| times 6 iff 3(2x-7)=2(x+6) iff 6x-21=2x+12 iff $
$iff 6x-2x=12+21 iff 4x=33 iff x= frac <33> <4>=8 frac 14$
Ответ: $8 frac 14$
Пример 6. Решите уравнение |x+1|=5
Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3
$$ |x + 1| = x + 3 iff left[ begin <left< begin x+1 ge 0 \ x+1=x+3 end right.>\ <left< begin x+1 Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?
Подставляем x=-3 в уравнение и решаем его относительно параметра a:
5a $cdot$ (-3) + 18 = 3 $iff$ -15a = 3 — 18 $iff$ -15a = -15 $iff$ a = -15:(-15)=1
Что такое уравнение и корни уравнения? Как решить уравнение?
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x= 2x -5
4+3x -2x =-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4 +3x-2x=-5
3x-2x=-5 -4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅ (-9) =2⋅ (-9) -5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
Далее делим все уравнение на 3.
3x :3 =45 :3
(3:3)x=15
Сделаем проверку. Подставим в уравнение найденный корень.
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
источники:
http://reshator.com/sprav/algebra/7-klass/uravnenie-i-ego-korni/
http://tutomath.ru/6-klass/chto-takoe-uravnenie-i-korni-uravneniya-kak-reshit-uravnenie.html
Общие свойства алгебраических уравнений Определение числа действительных корней алгебраического уравнения.
Общие
свойства алгебраического уравнения:
В
общем виде алгебраическое уравнение
может быть записано в виде:
Pn(x)
= a0
+ a1x
+ a2x2
+ … + anxn
.
где
Pn(x)
— многочлен
n-ой
степени, n
— наивысшая
степень при неизвестном, a0,
a1,
… , an
— действительные
коэффициенты.
Всякое
число x,
обращающее многочлен в ноль, т.е. Pn(x)
= 0 называется
корнем
многочлена. Согласно основной теореме
алгебры, многочлен Pn(x)
степени
n (n ³
1)
с любыми числовыми коэффициентами,
имеет n
корней,
если каждый из корней считать столько
раз, какова его кратность.
Число
x
является корнем многочлена Pn(x)
тогда и только тогда, когда Pn(x)
делится
без остатка на х — x
. Если
при этом Pn(x)
делится
без остатка на (х-x)k
(k ³1),
но уже не делится на (х-x)k+1,
то x
называется k-кратным
корнем
(или корнем
кратности k)
многочлена
Pn(x).
Корни
кратности k=1
называются
простыми
корнями
многочлена.
Прежде
чем вычислять корни алгебраического
уравнения, сначала необходимо:
а)
определить число корней, которое имеет
данное уравнение;
б)
найти область существования корней
(установить верхнюю и нижнюю границу
расположения корней).
Определение
числа действительных корней алгебраических
уравнений.
Для
этого используют правило Декарта:
Количество
действительных положительных корней
алгебраического уравнения Pn(x)
= 0 с действительными коэффициентами
либо равно числу перемен знака в
последовательности коэффициентов
уравнения Pn(x)
= 0, либо на четное число меньше (равные
нулю коэффициенты не учитываются).
Количество
отрицательных корней уравнения равно
числу перемен знака в последовательности
коэффициентов Pn(-x)
= 0 или на четное число меньше.
Пример:
x5
— 17x4 +
12x3
+ 7x2
— x + 1 = 0 .
Это
уравнение имеет пять корней (из них хотя
бы один является действительным).
Уравнение
является полным, последовательность
знаков коэффициентов уравнения такова:
+ , — , + , + , — , + . Знак изменяется четыре
раза — значит, положительных корней
будет либо четыре, либо два, либо ни
одного.
Заменив
х
на -х,
получим:
-x5
— 17x4
— 12x3
+ 7x2
+ x + 1 = 0
число
постоянств знака равно одному,
следовательно, уравнение имеет один
отрицательный корень.
Пример:
x6
— 3x4
+ x3
+ x2
— 1 = 0 .
Данное
уравнение имеет шесть корней;
последовательность знаков: + , — , + , + , —
. Имеет место три перемены знака;
следовательно, положительных корней
либо 3 либо 1.
Для
многочлена
Pn(-x)
= x6
— 3x4
— x3
+ x2
— 1 = 0 .
последовательность
знаков: + , — , — , + , — . Здесь также три
перемены знака — поэтому число отрицательных
корней либо 3, либо 1.
Нахождение области существования корней алгебраического уравнения
Правило
кольца — пусть
дано алгебраическое уравнение
Pn(x)
= a0
+ a1x
+ a2x2
+ … + anxn
, где
a0,
a1,
… , an
— действительные
коэффициенты, и пусть
A = max {½a0½,
½a1½,
… , ½an-1½}
, B = max {½a1½,
½a2½,
… , ½an½}
.
Тогда
корни уравнения заключены в круговом
кольце r
< ½x½
< R , где


При
этом r
— нижняя,
а R
— верхняя
граница положительных корней
алгебраического уравнения Pn(x)
= 0, и
—R,
-r —
соответственно
нижняя и верхняя граница отрицательных
корней.
Пример.
Определить границы корней уравнения
5x3
— 20x + 3 =
0 .
Здесь
½an½
= 5, A =
20 , ½a0½
= 3, B = 20,
т.е.

Тогда,
если действительные корни уравнения
5x3
— 20x + 3 + 0
существуют (а они обязательно существуют,
так как уравнение нечетной степени), то
они расположены в интервале (-5, 5); при
этом отрицательные корни лежат в
интервале (-5, -0.013), а положительные — в
интервале (0.013, 5).
Метод
Ньютона —
если при х
= с
многочлен
Pn(x)
= a0
+ a1x
+ a2x2
+ … + anxn
и
его производные Pn‘(x),
Pn»(x),
… принимают
положительные значения, то с
является верхней границей положительных
корней уравнения Pn(х)
= 0 .
Пример.
Методом
Ньютона определить верхнюю границу
положительных корней уравнения 8x4
— 32x2
—
32х
+ 1
= 0 .
Находим
P(x) = 8x4
— 32x2
—
32х
+ 1
; P'(x) = 32x3
— 16x —
32
;
P»(x)
= 96x2
— 16 ; P»’(x)
= 192x ; PIV(x)
= 192 .
Проверке
подлежат только значения x
> 0.
При
x=c=1
имеем
P(1)<
0. Значит
проводить далее проверку для х=1 не
следует.
Проверка
x=c=2:
P(2) > 0 ; P‘(x)
> 0 ; P»(x)
> 0 ; P»’(2)
> 0 : PIV(x)
> 0 .
Таким
образом, верхней границей положительных
корней является число R
= 2.
В качестве нижней границы можно взять
число, обратное R,
т.е.
r = 1/2 =
0.5 .
Необходимо
добавить оценку скорости сходимости
методов
Соседние файлы в папке 2
- #
- #
- #
- #
- #
- #
- #
- #
- #
Алгебра и начала математического анализа, 10 класс
Урок №11. Многочлен P(x) и его корень. Алгебраическое уравнение.
Перечень вопросов, рассматриваемых в теме
1) обобщенное понятие многочлена;
2) основные действия над многочленами;
3) определение алгебраического уравнения;
4) теорема Безу.
Глоссарий по теме
Многочлен Pn (x) = a n x n + a n – 1 x n – 1 + a n – 2 x n – 2 + … + a 1 x + a 0 , где a≠0, aₖ, k=0,1,2,3,…, aₖ,k=0,1,2,3,…,n — числа, x — переменная, называется многочленом n -ной степени .
Традиционно aₙ называется старшим коэффициентом, a₀ — свободным членом многочлена.
Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.
Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.
Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).
Следствие. Если число а является корнем многочлена Р(х), то многочлен
Рₙ(х)= a₀ x n + a 1 x n – 1 + … + a n – 1 x + a n делится без остатка на двучлен х-а.
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x1, x2, …, xn)=0,
где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнением над множеством F.
Степенью алгебраического уравнения называют степень многочлена P.
Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Общая теория многочленов многих переменных далеко выходит за рамки школьного курса.
Мы рассмотрим многочлены одной действительной переменной, да и то в простейших случаях. Рассмотрим многочлены одной переменной, приведённые к стандартному виду.
Многочлен ax + b, где a≠0, a, b — числа, x — переменная, называется многочленом первой степени.
Многочлен ax²+bx+c, где a≠0, a, b, c — числа, x — переменная, называется многочленом второй степени (квадратным трёхчленом, квадратичной функцией).
Многочлен ax³+bx²+cx+d, где a≠0, a, b, c, d — числа, x — переменная, называется многочленом третьей степени.
Вообще, многочлен Pn (x) = a n x n + a n – 1 x n – 1 + a n – 2 x n – 2 + … + a 1 x + a 0, где a≠0, aₖ, k=0,1,2,3,…, aₖ,k=0,1,2,3,…,n — числа, x — переменная, называется многочленом n -ной степени.
Традиционно aₙ называется старшим коэффициентом, а a₀ — свободным членом многочлена.
Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.
Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида
P(x1, x2, …, xn)=0,
где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнением над множеством F.
Степенью алгебраического уравнения называют степень многочлена P.
Например, уравнение
является алгебраическим уравнением четвертой степени от трёх переменных (с тремя неизвестными) над множеством вещественных чисел.
Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Теорема Безу, невзирая на кажущуюся простоту и очевидность, является одной из базовых теорем теории многочленов. В данной теореме алгебраические характеристики многочленов (они позволяют работать с многочленами как с целыми числами) связываются с их функциональными характеристиками (которые позволяют рассматривать многочлены как функции).
Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).
Доказательство. Разделим Р(х) c остатком на (x — а).
Получим Р(х)= (x — а)·Q(х) + R; по определению остатка, многочлен r либо равен 0, либо имеет степень, меньшую степени (x — a), т.е. меньшую 1. Но степень многочлена меньше 1 только в случае, когда она равна 0, и поэтому в обоих случаях R на самом деле является числом – нулем или отличным от нуля.
Подставив теперь в равенство Р(х)= (x — а)·Q(х) + R значение x = a, мы получим Р(a)= (a — а)Q(х) + R, P(a) = R, так что действительно R = P(a).
Эту закономерность отметил и математик Безу.
Следствие. Если число а является корнем многочлена Р(х), то многочлен
Рₙ(х)= a₀ x n + a 1 x n – 1 + … + a n – 1 x + a n делится без остатка на двучлен х-а.
Историческая справка
Этьенн Безу — французский математик, член Парижской Академии Наук (с 1758 года), родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года. С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.
Основные работы Этьенна Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений.
В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках.
Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный «Курс математики», написанный им в 1764-69 годах.
Безу развил метод неопределённых множителей. В элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе.
Часть трудов Безу посвящена внешней баллистике.
Именем ученого названа одна из основных теорем алгебры.
Примеры алгебраических уравнений
- алгебраическое уравнение с одним неизвестным -уравнение вида
, где n- натуральное число.
- Линейное уравнение от одной переменной ax+b=0, a
- Квадратное уравнение ax2+bx+c=0, a
.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Разложим на множители многочлен:
Решение: 
Ответ: 

Пример 2.
Решить уравнение: х4 — x3 — 6x2 — x + 3 = 0.
Решение: Целые корни многочлена Р(х) = х4 — x3 — 6x2 — x + 3 должны быть делителями свободного члена, так что это могут быть числа -1, 1, 3, -3.
Подберем корень по схеме Горнера:
|
1 |
-1 |
-6 |
-1 |
3 |
|
|
-1 |
1 |
-2 |
-4 |
3 |
0 |
х4 — x3 — 6x2 — x + 3= (х + 1)(х3 -2х2 – 4х +3) =0
|
1 |
-2 |
-4 |
3 |
|
|
-1 |
1 |
-3 |
-1 |
4 |
|
1 |
1 |
-1 |
-5 |
-2 |
|
-3 |
1 |
-5 |
11 |
-30 |
|
3 |
1 |
1 |
-1 |
0 |
Q(x) = х3 -2х2 – 4х +3=(x- 3)(x2 + x -1)=0
x2 + x -1 =0
D=5
Ответ: -1; 3;





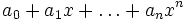
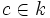 , который после подстановки его вместо
, который после подстановки его вместо 
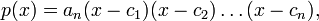
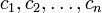 — (в общем случае комплексные) корни многочлена
— (в общем случае комплексные) корни многочлена 

 , где n- натуральное число.
, где n- натуральное число.
 .
.

