В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
- Нахождение координат вектора
- Примеры задач
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).
Формулы для определения координат вектора
| Для плоских задач | AB = {Bx — Ax; By — Ay} |
| Для трехмерных задач | AB = {Bx — Ax; By — Ay; Bz — Az} |
| Для n-мерных векторов | AB = {B1 — A1; B2 — A2; … Bn — An} |
Примеры задач
Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).
Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.
Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = ABx + Ax = 6 + 2 = 8.
By = ABy + Ay = 14 + 5 = 19.
Таким образом, B = (8; 19).
Нахождение координат вектора через координаты точек
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .
Векторы i → и j → называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.
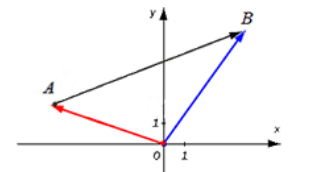
Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .
Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.
Изобразим координатную ось.
Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .
O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .
По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .
Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .
Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.
Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .
Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .
Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .
Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .
По условию известно, что A B → = ( 2 , 0 , — 2 ) .
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2
Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5
Ответ: B ( 5 , 5 , 5 ) .
Нахождение координат вектора
В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB , нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).
Формулы для определения координат вектора
» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
| Для плоских задач | AB = x — Ax; By — Ay> |
| Для трехмерных задач | AB = x — Ax; By — Ay; Bz — Az> |
| Для n-мерных векторов | AB = 1 — A1; B2 — A2; . Bn — An> |
Примеры задач
Задание 1
Найдем координаты вектора AB , если у его точек следующие координаты: , .
Задание 2
Определим координаты точки B вектора , если координаты точки .
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = AB x + Ax = 6 + 2 = 8.
By = AB y + Ay = 14 + 5 = 19.
Как найти вектор по точкам
ФОРМУЛА
Чтобы найти координаты вектора (
overline{A B}
)на плоскости, если он задан координатами его начала (
Aleft(x_{1} ; y_{1}right)
) и (
Bleft(x_{2} ; y_{2}right)
) конца, необходимо вычесть соответствующие координаты начала из координат конца, то есть
(
overline{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1}right)
)
Чтобы найти координаты вектора (
overline{A B}
), заданного в пространстве по координатам (
Aleft(x_{1} ; y_{1} ; z_{1}right)
) и (
Bleft(x_{2} ; y_{2} ; z_{2}right)
), необходимо, по аналогии с плоским случаем, вычесть координаты начала из координат конца:
(
overline{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1} ; z_{2}-z_{1}right)
)
ПРИМЕРЫ НАХОЖДЕНИЯ КООРДИНАТ ВЕКТОРА ПО ТОЧКАМ
ПРИМЕР
A(4 ;-1)
) и (
B(2 ; 1)
). Найти координаты векторов (
overline{A B}
) и (
overline{B A}
)
overline{A B}
) точка (
mathrm{A}
) является началом, а точка (
B
) — концом. Тогда координаты вектора (
overline{B A}
)равны
(
overline{A B}=(2-4 ; 1-(-1))=(-2 ; 2)
)
Для вектора (
overline{B A}
) точка (
B
) является началом, а точка (
mathrm{A}
) — концом. Тогда координаты вектора (
overline{B A}
)равны
(
overline{B A}=(4-2 ;-1-1)=(2 ;-2)
)
overline{A B}=(-2 ; 2)
)
(
overline{B A}=(2 ;-2)
)
ПРИМЕР
A(1 ;-2 ; 0,5)
) , (
B(3 ; 2 ; 1,5)
) и (
C(0 ;-1 ; 1)
). Найти координаты векторов (
overline{A B}, overline{A C}, overline{B C}
)
overline{A B}
) точка (
mathrm{A}
) является началом, а точка (
B
) — концом. Тогда координаты вектора (
overline{A B}
)соответственно равны:
(
overline{A B}=(3-1 ; 2-(-2) ; 1,5-0,5)=(2 ; 4 ; 1)
)
Для вектора (
overline{A C}
)точка (
mathrm{A}
) является началом, а точка (
mathrm{C}
) — концом. Тогда его координаты соответственно равны
(
overline{A C}=(0-1 ;-1-(-2) ; 1-0,5)=(-1 ; 1 ; 0,5)
)
Для вектора (
overline{B C}
) точка (
B
) является началом, а точка (
mathrm{C}
) — концом. Его координаты равны
(
overline{B C}=(0-3 ;-1-2 ; 1-1,5)=(-3 ;-3 ;-0,5)
)
overline{A B}=(2 ; 4 ; 1)
)
(
overline{A C}=(-1 ; 1 ; 0,5)
)
(
overline{B C}=(-3 ;-3 ;-0,5)
)
Определение
Вектор – это направленный отрезок, т.е. отрезок, имеющий длину и определенное направление. Графически вектор изображается в виде направленных отрезков определенной длины.
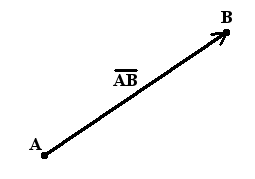
Вектор, имеющий начальную точку А и конечную точку В, обозначается [overrightarrow{A B}](рис. 1).
Определения
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора [overrightarrow{A B}]. Длина вектора [overrightarrow{A B}] обозначается как: [|overrightarrow{A B}|]
Векторы параллельные одной прямой или лежащие на одной прямой, называются коллинеарными векторами.
Определение
Единичный вектор или орт — это вектор, длина которого равна единице.
Правило нахождения координат вектора
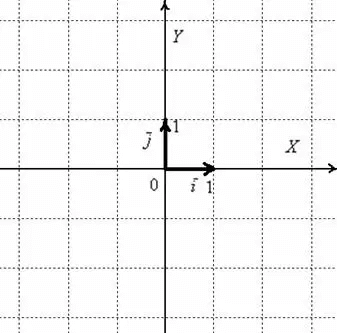
Отложим от начала системы координат два единичных вектора, то есть векторы, длины которых равны единице. Направление вектора [bar{i}] должно совпадать с осью [O x], а направление вектора [bar{j}] с осью [O y].
Векторы [bar{i}, bar{j}] — рассматриваемые векторы называются векторами координат или ортами. Эти векторы образуют базис поверхности. Иногда построенный базис называют ортонормированным базисом плоскости.
Обозначение: базис обычно пишется в круглых скобках, внутри которых в строгом порядке перечисляются векторы.
Любой вектор плоскости выражается по формуле нахождения координат вектора:
[vec{v}=v_{1} cdot vec{i}+v_{2} cdot vec{j}]
Где числа в этом базисе называются векторными координатами. Но само выражение называется векторным разложением.
Как выразить вектор через его координаты
Чтобы выразить вектор [overrightarrow{A B}(a, b)], где [Aleft(x_{1} ; y_{1}right)], а [Bleft(x_{2} ; y_{2}right)], сначала вычислим разницу между абсциссами [x], чтобы получить [a], затем вычислим разницу между ординатами [y], чтобы получить [b]:
[overrightarrow{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1}right)]
Пример 1
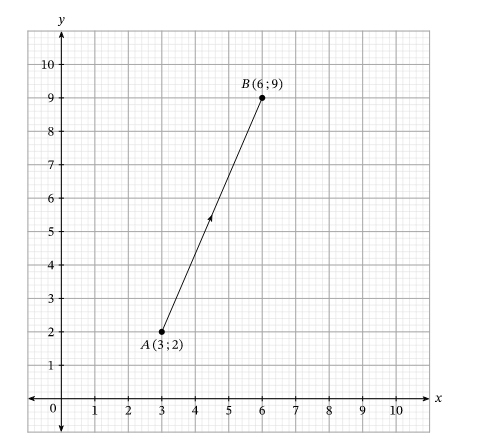
Найти координаты [overrightarrow{A B}] при значении координат точек [A(3 ; 2), B(6 ; 9)].
Решение:
Горизонтальное расстояние равно разнице между абсциссами [x], т.е. 6−3=3. Вертикальное расстояние равно разнице между ординатами [y], где 9−2=7.
Поэтому мы можем обозначить вектор от А до В как:
[overrightarrow{A B}=(3 ; 7)]
Нахождение координат вектора в пространстве
Теперь рассмотрим векторы в трехмерном пространстве, здесь все почти так же, как на плоскости, но будет добавлена только одна дополнительная координата.
Любой вектор в пространстве выражается следующим образом:
[vec{v}=v_{1} cdot vec{i}+v_{2} cdot vec{j}+v_{3} cdot vec{k}], где координаты вектора (числа) в заданном базисе.
Пример 2
Нужно найти вектор, соединяющий точку А (начало) с координатами (4, 5, 6) с точкой В (конец) с координатами (10, 11, 12).
Решение:
Вектор направлен из точки А в точку В и может быть обозначен как [overrightarrow{A B}]. Таким образом:
[overrightarrow{A B}=(10-4) ;(11-5) ;(12-6)=(6 ; 6 ; 6)]
Нет времени решать самому?
Наши эксперты помогут!
Как записать вектор на основе единичных векторов
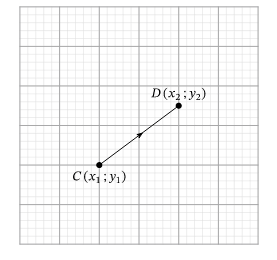
Если мы перейдем от начальной точки к конечной точке [Cleft(x_{y} ; y_{1}right) Dleft(x_{2} ; y_{2}right)], это описывает вектор, который представляет собой смещение на расстояние в направлении [overrightarrow{C D}left(x_{2}-x_{1}right) x] затем с расстояния в направлении [left(y_{2}-y_{1}right) y].
Мы можем обозначить этот вектор двумя способами:
[overrightarrow{C D}=left(x_{2}-x_{1}, y_{2}-y_{1}right)] или [overrightarrow{C D}=left(x_{2}-x_{1}right) i+left(y_{2}-y_{1}right) vec{j}]
Пример 3
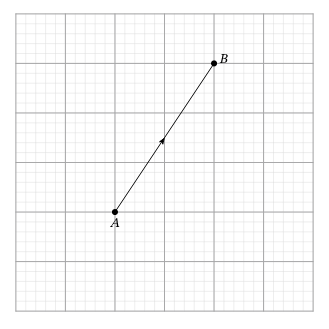
Выразить вектор в виде суммы единичных векторов.
Зная, что каждый квадрат сетки имеет длину 1, представим вектор [overrightarrow{A B}] как [a vec{i}+b vec{j}].
Решение:
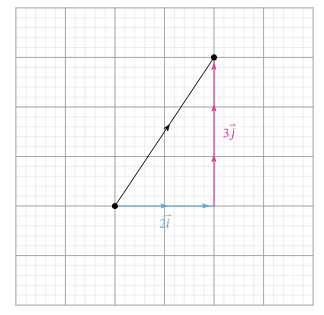
Из точки [A](начало), мы перемещаем единицы в горизонтальном направлении (которое представляет собой вектор), затем мы перемещаем единицы в вертикальном направлении (что представляет собой вектор), чтобы перейти к точке [B+2(2 vec{i}) u+3(3 vec{j})].
Вектор [overrightarrow{A B}] что представляет собой прямое движение от [A] к [B] , тогда равна сумме этих единичных векторов.
Как результат: [overrightarrow{A B}=2 vec{i}+3 vec{j}=(2,3)].
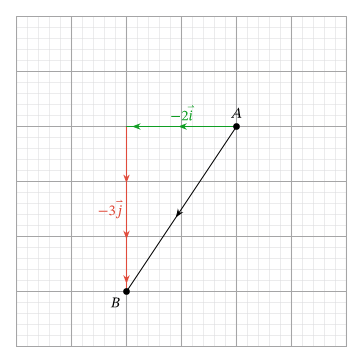
Использование векторов и позволяет описать вектор в соответствии с количеством шагов по горизонтали и вертикали длиной 1, которые необходимо сделать, чтобы пройти от начала до конца. Обратите внимание, что отрицательные коэффициенты представляют движение влево или вниз соответственно.
Например, приведенный выше вектор, представляющий смещение на -2 единицы в направлении и на -3 единицы в направлении [overrightarrow{A B}=(-2 ;-3) x y] или [(-2 vec{i})+(-3 vec{j})].
[overrightarrow{A B}=-2 vec{i}-3 vec{j}]
Важно
Следует понимать разницу между координатами точки и векторными координатами:
Координаты точки — это обычные координаты в прямоугольной системе координат. Каждая точка имеет строгое место на карте, и их нельзя никуда перемещать.
Координаты вектора — это его разложение относительно основания.
Любой вектор свободен, поэтому при желании или необходимости мы легко можем отложить его от другой точки плоскости. Записи координат точек и векторных координат выглядят одинаков, а значение координат совсем разные.
Координаты равных векторов соответственно равны.
Если точка начала вектора не совпадает с началом системы координат, тогда рассмотрим задачу. На оси [O_{x y}] заданы координаты точек вектора, где [Aleft(x_{a} ; y_{a}right)] и [Bleft(x_{b} y_{b}right)]. Найти координаты [overrightarrow{A B}].
Зная формулу сложения векторов, имеем [overrightarrow{O A}+overrightarrow{A B}=overrightarrow{O B}], следует: [overrightarrow{A B}=overrightarrow{O B}-overrightarrow{O A}].
[overrightarrow{O A}] и [overrightarrow{O B}] радиус-векторы точек А и В, следовательно, координаты точек: [overrightarrow{O A}=left(x_{a}, y_{a}right), overrightarrow{O B}=left(x_{b} ; y_{b}right)].
Способы вычисления координат вектора
Содержание:
- Что такое координаты вектора — какие операции можно производить
- Способы представления, как записываются
- Методы вычисления координат вектора
- Примеры задачи на нахождение координат вектора
Что такое координаты вектора — какие операции можно производить
Три попарно перпендикулярные прямые с определенными направлениями и единицей измерения в геометрии составляют систему координат в пространстве. Точка, в которой пересекаются данные прямые, представляет собой начало координат.
Оси координат:
- (Ox) — ось абсцисс.
- (Oy) — ось ординат.
- (Oz) — ось аппликат.
Через две прямые, которые пересекаются, можно построить плоскость. Таким образом, образуются три координатные плоскости в виде:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- ((Oxy));
- ((Oyz));
- ((Oxz)).
Определить положение точки (А) в пространстве можно с помощью трех координат (x, y) и (z).
Координата x является понятием абсциссы точки (A), координата y — определяет ординату точки (A), координата (z) — аппликату точки (A).
Запись имеет следующий вид:
(A(x;y;z)).
Варианты расположения точки:
- в том случае, когда точка расположена на оси (Ox), ее координаты — (X(x;0;0));
- при нахождении точки на оси (Oy) она характеризуется координатами (Y(0;y;0));
- если точка принадлежит оси (Oz), ее координаты — (Z(0;0;z));
- точка, лежащая в плоскости (Oxy), обладает координатами (A1(x;y;0));
- в том случае, когда расположение точки совпадает с плоскостью (Oyz,) она обладает координатами (A2(0;y;z));
- если точка расположена в плоскости (Oxz), то данная точка имеет координаты ( A3(x;0;z)).
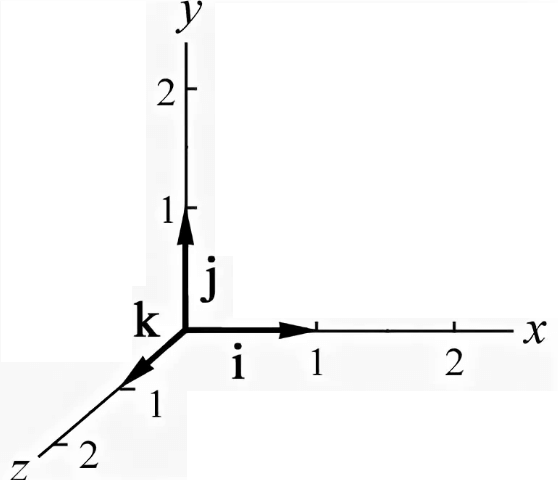
Допустим, что в системе координат существуют некие единичные векторы (overrightarrow { i }), (overrightarrow { j }) и (overrightarrow { k }), которые были отложены от начала координат. В этом случае допустимо определить прямоугольный базис. Какой-либо вектор раскладывается на единичные вектора и записывается в виде:
(overrightarrow {OA}=x⋅overrightarrow { i }+y⋅overrightarrow { j }+z⋅overrightarrow { k })
Коэффициенты (x), (y) и ( z) могут иметь одно единственное значение и являются координатами вектора.
Определение
В прямоугольной системе координат (Х0у) проекции х и у вектора (overrightarrow {OA}) на оси абсцисс и ординат называют координатами вектора. То есть координаты вектора являются числами, описывающими положение вектора относительно координатной плоскости.
Координатами вектора, начало которого совпадает с точкой (A(x1; y1)), а конец — соответствует точке (B(x2; y2)), называют числа:
(a1 = x2 — x1);
(a2 = y2 — y1).
Координаты вектора записывают в таком виде:
(overrightarrow {OA}{x;y;z}).
Правила записи с помощью координат:
Координаты суммы векторов при наличии известных координат векторов:
Координаты разности векторов при заданных координатах векторов:
Координаты произведения вектора на число при наличии определенных координатах вектора:
Длина, которой обладает вектор:
Координаты вектора при заданных координатах, которыми характеризуются начальная и конечная точки вектора:
Расстояние по модулю, на которое удалены две точки с заданными координатами:
Координаты серединной точки отрезка, когда заданы координаты начальной и конечной точек отрезка:
Координаты вектора обладают следующими свойствами:
- Какие-либо равные векторы в единой системе координат обладают идентичными координатами.
- Координаты коллинеарных векторов пропорциональны в том случае, когда ни один из векторов не обладает нулевым значением.
- Квадрат длины какого-либо вектора определяется как сумма квадратов его координат.
- В процессе умножения вектора на действительное число каждая его координата умножается на это число.
- Когда требуется сложить вектора, следует определить сумму соответствующих координат данных векторов.
- Скалярное произведение пары векторов соответствует сумме произведений их соответствующих координат.
Способы представления, как записываются
Общепринятой является запись координат вектора в виде:
((х, у)).
Непосредственно вектор обозначают, как:
(overrightarrow {AB} =(х, у)).
Координаты вектора записывают в круглых скобках рядом с буквенным обозначением вектора:
(overrightarrow {AB} (a_1 ;a_2 ))
или
(overrightarrow a (a_1 ;a_2 ))
В некоторых случаях допустимо использовать запись координат вектора без буквенного обозначения, то есть со знаком вектора над скобками:
(overrightarrow {(a_1 ;a_2 )})
Нулевой вектор обладает нулевыми координатами:
(overrightarrow 0 (0;0))
Методы вычисления координат вектора
В том случае, когда определены координаты начала и конца вектора (overline{AB}: Aleft(x_{1} ;; y_{1} right),; Bleft(x_{2} ;; y_{2} right)), при вычислении его координат требуется от координат конца отнять соответствующие координаты начала:
(overline{AB}=left(x_{2} -x_{1} ;; y_{2} -y_{1} right))
Формула определения координат вектора для двухмерных задач: в рассматриваемом случае вектор ( overline{AB} )с заданными координатами точек (A(х1;у1) и B(x2;y2)) можно найти по формуле:
(overline{AB}=(x2 – x1 ; y2 – y1).)
Формула определения координат вектора для пространственных задач: если требуется решить пространственную задачу на нахождение вектора (overline{AB}), координаты точек (A(х1;у1;z1) и B(x2;y2;z2)) которого известны, следует воспользоваться формулой:
(overline{AB}=(x2 – x1 ; y2 – y1; z2 – z1))
С помощью вычисления координат вектора можно определить его характеристики, в том числе найти длину вектора. Зная координаты, достаточно просто построить вектор.
Примеры задачи на нахождение координат вектора
Задача 1
Существуют пары точек:
(A(-3; 7), B(2; -1));
(С(5; 0), D(11; 8).
)
Необходимо определить координаты векторов:
(overrightarrow {AB} ,overrightarrow {CD} .)
Решение:
С целью вычисления координат вектора необходимо из координат его конца (точки B) вычесть координаты начала (точки A):
(overrightarrow {AB} (2 — ( — 3); — 1 — 7))
(overrightarrow {AB} (5; — 8).)
Аналогичным способом можно рассчитать координаты второго вектора:
(overrightarrow {CD} (11 — 5;8 — 0))
(overrightarrow {CD} (6;8))
Ответ: (overrightarrow {AB} (5; — 8); overrightarrow {CD} (6;8).)
Задача 2
Требуется вычислить координаты вектора (overline{AB}) при условии, что:
(Aleft(-1;; 2right), Bleft(2;; -3right))
Решение
Определить координаты, которым характеризуется вектор (overline{AB}), исходя из известных по заданию координат его начальной точки (Aleft(-1;; 2right)) и конечной точки (Bleft(2;; -3right)), можно путем вычитания из координат конечной точки соответствующих координат начальной точки. Таким образом, первым и единственным действием в данном случае является:
(overline{AB}=left(2-left(-1right), ;; -3-2right)=left(3;; -5right))
Ответ: (overline{AB}=left(3;; -5right))
Задача 3
Необходимо определить координаты точки (A), которая представляет собой начало вектора (overline{AB}=left(0;; -4;; 3right)), а концом вектора является точка (Bleft(-1;; 6;; 1right).)
Решение
Предположим, что точка (A ) обладает следующими координатами:
(Aleft(a_{1} ;; a_{2} ;; a_{3} right))
В таком случае, вектор (overline{AB}), при условии, что точка (Bleft(-1;; 6;; 1right)), характеризуется следующими координатами:
(overline{AB}=left(-1-a_{1} ;; 6-a_{2} ;; 1-a_{3} right)=left(0;; -4;; 3right))
Зная, что равенство двух векторов достигается при равенстве соответствующих координат этих векторов, можно записать следующие уравнения для вычисления неизвестных координат, которыми характеризуется точка (А):
(-1-a_{1} =0Rightarrow a_{1} =-1)
(6-a_{2} =-4Rightarrow a_{2} =10)
(1-a_{3} =3Rightarrow a_{3} =-2)
В результате:
(Aleft(-1;; 10;; -2right))
Ответ: (Aleft(-1;; 10;; -2right))