Как найти координаты точки на единичной окружности

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

• Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
• Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
• В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
• В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

• 2π радиан = 360°
• 1 радиан = (360/2π) градусов
• 1 радиан = (180/π) градусов
• 360° = 2π радиан
• 1° = (2π/360) радиан
• 1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Теория: 06 Вычисление координат точки на единичной окружности

На единичной окружности отмечена точка (displaystyle A <small ,>) как показано на рисунке. Угол (displaystyle BOA ) равен (displaystyle color<alpha> <small .>) Найдите абсциссу точки (displaystyle A <small .>)

Абсцисса точки (displaystyle A) равна Перетащите сюда правильный ответ .

Так как отрезок (displaystyle AB) перпендикулярен оси (displaystyle rm OX<small,>) то абсцисса точки (displaystyle A) равна длине отрезка (displaystyle OB<small.>)

Найдем длину отрезка (displaystyle OB<small.>)

Рассмотрим прямоугольный треугольник (displaystyle AOB<small,>) катетом которого является отрезок (displaystyle OB<small.>)

Гипотенуза (displaystyle OA) треугольника (displaystyle AOB) является радиусом единичной окружности.

Значит, (displaystyle OA=1<small.>)

Тогда, поскольку (displaystyle OB) – катет, прилежащий к углу (displaystyle color<alpha><small,>) то

Таким образом, получаем:

абсцисса точки (displaystyle A) (displaystyle = OB=cos(color<alpha>)<small.>)

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac<4>=frac<2pi r><4>=frac<pi r><2>.) Тогда радианная мера угла: $$ angle AOB=frac>=frac<pi r><2cdot r>=frac<pi> <2>$$

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например:

Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<pi><4>, frac<pi><2>, frac<2pi><3>, pi), а также (-frac<pi><6>, -frac<pi><4>, -frac<pi><2>, -frac<2pi><3>, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<13pi><6>, frac<25pi><6>), и (-frac<11pi><6>). Все четыре точки совпадают, т.к. begin Mleft(frac<pi><6>right)=Mleft(frac<pi><6>+2pi kright)\ frac<pi><6>-2pi=-frac<11pi><6>\ frac<pi><6>+2pi=frac<13pi><6>\ frac<pi><6>+4pi=frac<25pi> <6>end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -frac<pi> <6>lt t lt frac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi klt tltfrac<pi><3>+2pi k $$
Интервал
$$ -frac<pi> <6>leq t leq frac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi kleq tleqfrac<pi><3>+2pi k $$
Полуинтервал
$$ -frac<pi> <6>leq t ltfrac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi kleq tltfrac<pi><3>+2pi k $$

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^<circ>=frac<pi><6>.\ EC=60^<circ>=frac<pi><3>.\ AE=EC+CD=90^<circ>+30^<circ>=120^<circ>=frac<2pi><3>.\ ED=EC+CD=60^<circ>+90^<circ>=150^<circ>=frac<5pi><6>. end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<pi><2>; frac<3pi><4>; frac<7pi><6>; frac<7pi><4>).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac<pi><2>=-90^<circ>, frac<3pi><4>=135^<circ>\ frac<7pi><6>=210^<circ>, frac<7pi><4>=315^ <circ>end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<11pi><2>; 5pi; frac<17pi><6>; frac<27pi><4>).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac<11pi><2>=frac<-12+1><2>cdotpi=-6pi+frac<pi><2>rightarrow frac<pi><2>=90^<circ>\ 5pi=4pi+pirightarrow pi=180^<circ>\ frac<17pi><6>=frac<18-1><6>pi=3pi-frac<pi><6>rightarrow pi-frac<pi><6>=frac<5pi><6>\ frac<27pi><4>=frac<28-1><4>pi=7pi-frac<pi><4>rightarrow pi-frac<pi><4>=frac<3pi> <4>end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac<3,14><2>=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac<3pi><2>approx frac<3cdot 3,14><2>=4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac<3pi> <2>Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac<3pi><2>lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

Единичная числовая окружность на координатной плоскости

1. Понятие тригонометрии
2. Числовая окружность
3. Градусная и радианная мера угла
4. Свойства точки на числовой окружности
5. Интервалы и отрезки на числовой окружности
6. Примеры

п.1. Понятие тригонометрии

Тригонометрия – это раздел математики, в котором изучаются тригонометрические функции и их использование.

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета, ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным; по часовой стрелке – отрицательным.

Например:

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90&deg, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Радианной мерой угла называется отношение длины дуги окружности, заключенной между сторонами угла и центром в вершине угла, к радиусу этой окружности.
От радиуса окружности это отношение не зависит.

Например:

Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_{AB}=frac{L}{4}=frac{2pi r}{4}=frac{pi r}{2}.) Тогда радианная мера угла: $$ angle AOB=frac{l_{AB}}{r}=frac{pi r}{2cdot r}=frac{pi}{2} $$

$$ 1^{circ}=frac{pi}{180}text{рад}, 1 text{рад}=frac{180^{circ}}{pi}approx 57,3^{circ} $$

Таблица соответствия градусных и радианных мер некоторых углов

30°	45°	60°	90°	120°	135°	150°	180°	270°	360°
(frac{pi}{6})	(frac{pi}{4})	(frac{pi}{3})	(frac{pi}{2})	(frac{2pi}{3})	(frac{3pi}{4})	(frac{5pi}{6})	(pi)	(frac{3pi}{2})	(2pi)

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t<0 двигаемся по окружности по часовой стрелке, описывая дугу ⌒ AM=t. Точка M — искомая.

Например:

Отметим на числовой окружности точки, соответствующие (frac{pi}{6}, frac{pi}{4}, frac{pi}{2}, frac{2pi}{3}, pi), а также (-frac{pi}{6}, -frac{pi}{4}, -frac{pi}{2}, -frac{2pi}{3}, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Каждой точке M(t) на числовой окружности соответствует бесконечное множество действительных чисел t с точностью до полного периода 2π:
$$ M(t) = M(t+2pi k), kinmathbb{Z} $$

Например:

Отметим на числовой окружности точки, соответствующие (frac{pi}{6}, frac{13pi}{6}, frac{25pi}{6}), и (-frac{11pi}{6}). Все четыре точки совпадают, т.к. begin{gather*} Mleft(frac{pi}{6}right)=Mleft(frac{pi}{6}+2pi kright)\ frac{pi}{6}-2pi=-frac{11pi}{6}\ frac{pi}{6}+2pi=frac{13pi}{6}\ frac{pi}{6}+4pi=frac{25pi}{6} end{gather*}

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Например:

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin{gather*} BE=30^{circ}=frac{pi}{6}.\ EC=60^{circ}=frac{pi}{3}.\ AE=EC+CD=90^{circ}+30^{circ}=120^{circ}=frac{2pi}{3}.\ ED=EC+CD=60^{circ}+90^{circ}=150^{circ}=frac{5pi}{6}. end{gather*}

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac{pi}{2}; frac{3pi}{4}; frac{7pi}{6}; frac{7pi}{4}).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin{gather*} -frac{pi}{2}=-90^{circ}, frac{3pi}{4}=135^{circ}\ frac{7pi}{6}=210^{circ}, frac{7pi}{4}=315^{circ} end{gather*}

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac{11pi}{2}; 5pi; frac{17pi}{6}; frac{27pi}{4}).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin{gather*} -frac{11pi}{2}=frac{-12+1}{2}cdotpi=-6pi+frac{pi}{2}rightarrow frac{pi}{2}=90^{circ}\ 5pi=4pi+pirightarrow pi=180^{circ}\ frac{17pi}{6}=frac{18-1}{6}pi=3pi-frac{pi}{6}rightarrow pi-frac{pi}{6}=frac{5pi}{6}\ frac{27pi}{4}=frac{28-1}{4}pi=7pi-frac{pi}{4}rightarrow pi-frac{pi}{4}=frac{3pi}{4} end{gather*}

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin{gather*} 0, fracpi2approxfrac{3,14}{2}=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac{3pi}{2}approx frac{3cdot 3,14}{2}=4,71, 2piapprox 6,28 end{gather*}

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac{3pi}{2} Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac{3pi}{2}lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb{Z})), запишите количество полученных базовых точек.

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

Сегодня поговорим об единичной окружности 🧑‍🏫

Можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота?🤔

Ну, конечно, можно! Записывай и запоминай общую формулу для нахождения координат точки:

x=x0+r⋅cos δ

y=y0+r⋅sin δ

x0,y0 — координаты центра окружности;

r — радиус окружности;

δ —угол поворота радиуса вектора.

При изучении тригонометрии в школе каждый ученик сталкивается с весьма интересным понятием «числовая окружность». От умения школьного учителя объяснить, что это такое, и для чего она нужна, зависит, насколько хорошо ученик поймёт тригонометрию впоследствии. К сожалению, далеко не каждый учитель может доступно объяснить этот материал. В результате многие ученики путаются даже с тем, как отмечать точки на числовой окружности. Если вы дочитаете эту статью до конца, то научитесь делать это без проблем.

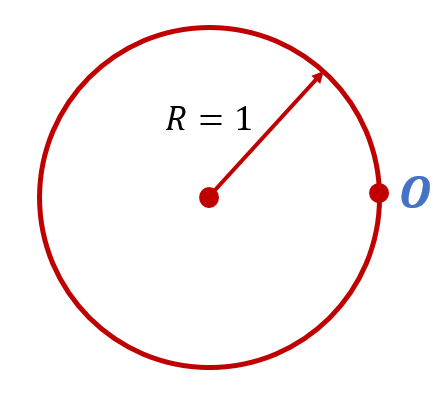
Итак, приступим. Нарисуем окружность, радиус которой равен 1. Самую «правую» точку этой окружности обозначим буквой O:

Поздравляю, вы только что нарисовали единичную окружность. Поскольку радиус этой окружности равен 1, то её длина равна .

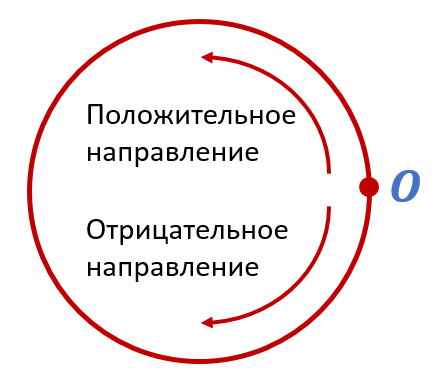
Каждому действительному числу можно поставить в соответствие длину траектории вдоль числовой окружности от точки O. За положительное направление принимается направление движения против часовой стрелки. За отрицательное – по часовой стрелке:

Расположение точек на числовой окружности

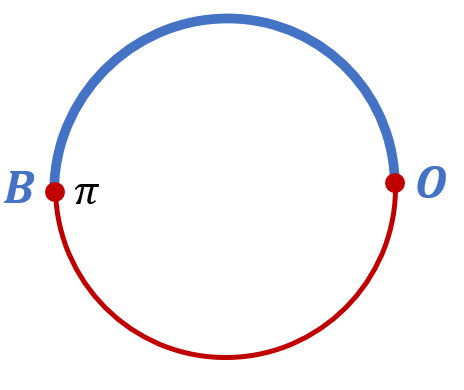
Как мы уже отмечали, длина числовой окружности (единичной окружности) равна . Где тогда будет располагаться на этой окружности число ? Очевидно, от точки O против часовой стрелки нужно пройти половину длины окружности, и мы окажемся в нужной точке. Обозначим её буквой B:

Обратите внимание, что в ту же точку можно было бы попасть, пройдя полуокружность в отрицательном направлении. Тогда бы мы отложили на единичной окружности число . То есть числам и соответствует одна и та же точка.

Причём этой же точке соответствуют также числа , , , и, вообще, бесконечное множество чисел, которые можно записать в виде , где , то есть принадлежит множеству целых чисел. Всё это потому, что из точки B можно совершить «кругосветное» путешествие в любую сторону (добавить или вычесть длину окружности ) и попасть в ту же самую точку. Получаем важный вывод, который нужно понять и запомнить.

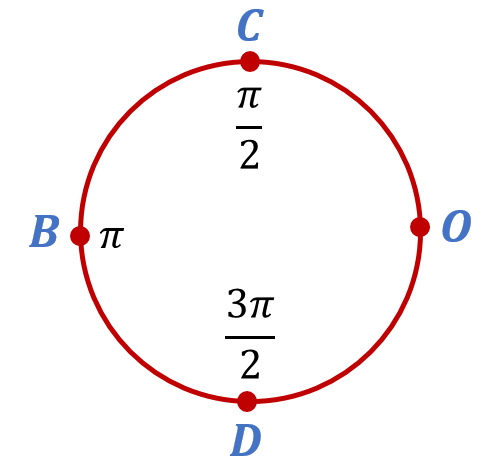
Разобьем теперь верхнюю полуокружность числовой окружности на дуги равной длины точкой C. Легко видеть, что длина дуги OC равна . Отложим теперь от точки C дугу той же длины в направлении против часовой стрелки. В результате попадём в точку B. Результат вполне ожидаемый, поскольку . Отложим эту дугу в том же направлении ещё раз, но теперь уже от точки B. В результате попадём в точку D, которая будет уже соответствовать числу :

Заметим опять, что эта точка соответствует не только числу , но и, например, числу , потому что в эту точку можно попасть, отложив от точки O четверть окружности в направлении движения часовой стрелки (в отрицательном направлении).

И, вообще, отметим снова, что этой точке соответствует бесконечно много чисел, которые можно записать в виде . Но их также можно записать в виде . Или, если хотите, в виде . Все эти записи абсолютно равнозначны, и они могут быть получены одна из другой.

Разобьём теперь дугу на OC пополам точкой M. Сообразите теперь, чему равна длина дуги OM? Правильно, вдвое меньше дуги OC. То есть . Каким числам соответствует точка M на числовой окружности? Уверен, что теперь вы сообразите, что эти числа можно записать в виде .

Но можно и иначе. Давайте в представленной формуле возьмём . Тогда получим, что . То есть эти числа можно записать в виде . Этот же результат можно было получить, используя числовую окружность. Как я уже говорил, оба записи равнозначны, и они могут быть получены одна из другой.

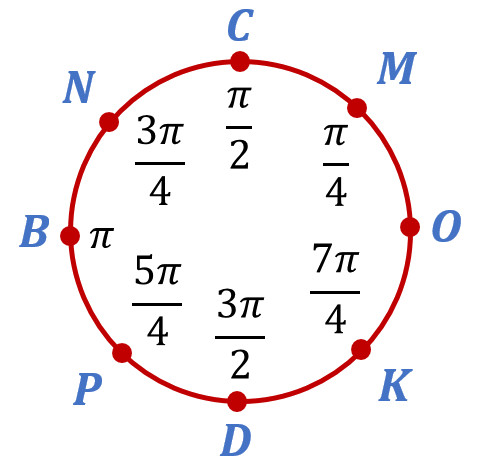
Теперь вы легко можете привести пример чисел, которым соответствуют точки N, P и K на числовой окружности. Например, числам , и :

Часто именно минимальные положительные числа и берут для обозначения соответствующих точек на числовой окружности. Хотя это совсем не обязательно, и точке N, как вы уже знаете, соответствует бесконечное множество других чисел. В том числе, например, число .

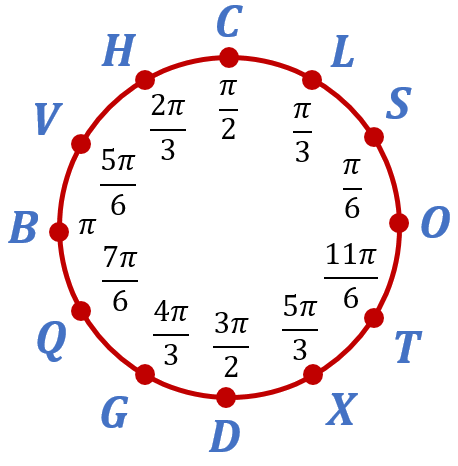
Если разбить дугу OC на три равные дуги точками S и L, так что точка S будет лежать между точками O и L, то длина дуги OS будет равна , а длина дуги OL будет равна . Используя знания, которые вы получили в предыдущей части урока, вы без труда сообразите, как получились остальные точки на числовой окружности:

Числа не кратные π на числовой окружности

Зададимся теперь вопросом, где на числовой прямой отметить точку, соответствующую числу 1? Чтобы это сделать, надо от самой «правой» точки единичной окружности O отложить дугу, длина которой была бы равна 1. Указать место искомой точки мы можем лишь приблизительно. Поступим следующим образом.

Мы знаем, где на числовой прямой находится точка L, соответствующая числу . Мы также знаем приблизительное значение числа . Тогда, очевидно, число чуть больше 1. Следовательно, точка, которая соответствует числу 1, расположена на числовой окружности чуть ближе к точке O, чем точка L:

Отмеченной точке, как мы уже знаем, соответствуют также числа .

Таким образом, на сегодняшнем уроке мы усвоили, что каждому числу соответствует какая-то точка на числовой окружности, но каждой точке числовой окружности соответствует бесконечное множество чисел. Запомните это, чтобы не путаться в дальнейшем при изучении тригонометрии.

Надеюсь, вы усвоили этот урок. Чтобы убедиться в этом, выполните самостоятельно следующие упражнения. Возникшие вопросы обсудим с вами в комментариях:

• Выделите на числовой окружности дугу, все точки которой удовлетворяют условию:

• Как расположены точки на числовой окружности, соответствующие числам:

a) и ;

б) и ;

в) и ;

г) и ?

Материал подготовил репетитор по физике и математике в Москве, Сергей Валерьевич