Содержание:
Система координат в пространстве
Декартова система координат в пространстве
Вы познакомились с декартовой системой координат на плоскости в предыдущих классах. Систему координат в пространстве введём аналогично тому, как это было сделано на плоскости. Рассмотрим три взаимно перпендикулярных оси Ох, Оу и Оz, пересекающихся в точке О, являющейся началом координат. Через каждую пару этих прямых проведём плоскости Оху, 0xz и Оуz (рис. 1). Таким образом вводится система координат в пространстве, при этом
точку О — называют началом координат, прямые Ох, Оу и Оz — осями координат, Ох — ось абсцисс, Оу — ось ординат и Оz — ось аппликат, плоскости Оху, Оуz и Охz — координатными плоскостями.
Координатные плоскости делят пространство на 8 октант (получетвертей) (рис. 1).
Пусть в пространстве задана произвольная точка А. Через эту точку проведём плоскости, перпендикулярные плоскостям Охz, Оуz и Охz (рис. 2). Одна из этих плоскостей пересечёт ось Ох в точке Ах.
Координату Ах на оси Ох называют координатой х или абсциссой точки А.
Аналогично определяют у — координату (ординату) и z- координату (аппликату) точки А.
Координаты точки А записывают в виде А (х; у; z) или короче (х; у; z). Точки, изображённые на рисунке 3, имеют следующие координаты: А (0; 5; 0), B (4; 0; 0), М (0; 5; 4), К (2; 3; 4), Р (-2; 3; -4).
Пример:
Пусть в пространстве в декартовой системе координат
задана точка А (2; 3; 4). Где она расположена?
Решение:
От начала координат в положительном направлении осей Ох и Оу отложим отрезки ОАх = 2 и ОАу = 3 (рис. 4).
Через точку Ах проведём прямую, лежащую в плоскости Оху и параллельную оси Оу. А через точку Аy проведём прямую, лежащую в плоскости Оху и параллельную оси Ох. Точку пересечения этих прямых обозначим A1 . Через точку A1 проведём прямую, перпендикулярную плоскости Оху и на ней в положительном направлении Oz отложим отрезок АА1 = 4. Тогда точка А (2; 3; 4) и будет искомой точкой.
Пользуясь системой координат, созданной для современных программируемых станков и автоматизированных роботов, составляются программы, на основе которых обрабатываются металлы (рис. 5).
Расстояние между двумя точками
Пусть заданы две точки А (х1; у1; z1) и B (х2; у2; z2).
1.Сначала рассмотрим случай, когда прямая АВ не параллельна оси Оz (рис. 6). Через точки А и В проведём прямые, параллельные оси Оz. И пусть они пересекают плоскость Оху в точках Аz и Вz .
Координаты х и у этих точек соответственно равны координатам х и у точек А, В, а координаты z равны 0.
Теперь через точку В проведём плоскость а, параллельную плоскости Оху. Она пересечёт прямую ААz в некоторой точке С.
По теореме Пифагора: АВ2 = АС2 + СВ2.
Однако
Поэтому
2.Пусть отрезок АВ параллелен оси Оz, тогда 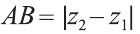
х1= х2 , у1 = у2 , мы опять приходим к вышеприведённой формуле.
Следовательно, расстояние между двумя точками А и В:
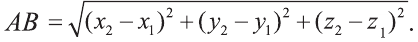
Примечание. Формула (1) выражает длину диагонали прямоугольного параллелепипеда, измерения которого равны
Уравнение сферы и шара
Известно, что множество всех точек М (х; у; z), расположенных на расстоянии R от данной точки А (а; Ь; с) образуют сферу (рис. 7). Тогда по формуле (1) координаты всех точек, расположенных на сфере радиуса R с центром в точке А (а; b; с), удовлетворяют равенству
Отсюда, ясно, что неравенство для точек шара радиуса R с центром в
точке А (а; b; с) имеет вид:
Пример:
Найдите периметр треугольника ABC с вершинами в
точках А (9; 3; -5), В (2; 10; -5), С (2; 3; 2).
Решение:
Р=АВ+АС+ВС периметр треугольника ABC. Воспользовавшись формулой 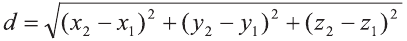
Следовательно, треугольник ABC равносторонний и его периметр 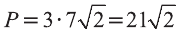
Ответ:
Координаты середины отрезка
Пусть А (x1; y1;z1) и В (х2; у2; z2) — произвольные точки, точка С (х; у; z) середина отрезка AB (рис. 8).
Через точки А, В и С проведём прямые, параллельные оси пересекающие плоскость Оху в точках 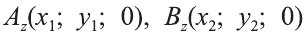
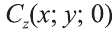
Отсюда по формулам нахождения координат середины отрезка на плоскости
Чтобы найти координату z, нужно вместо плоскости Оху рассмотреть плоскость 0xz или Оуz.
Тогда и для z получим формулу, подобную вышеприведённой.
Аналогично, используя координаты концов A и B отрезка AB, по формулам
находят координаты точки Р(х1;у]; г,), делящей отрезок АВ в отношении X САР: РВ = X).
Задача 3. Докажите, что четырёхугольник МЛШЬ с вершинами М{3; 6; 4), N(0; 2; 4), К(3; 2; 8), 1(6; 6; 
Доказательство: Для решения задачи используем признак параллелограмма: Четырёхугольник, точка пересечения диагоналей которого делит их пополам, является параллелограммом.
Координаты середины отрезка МК:
Координаты середины отрезка NL:
Координаты середин отрезков МК и NL равны. Это говорит о том, что отрезки пeрeсeкаются и в точке пeрeсeчeния делятся пополам. Следовательно, четырёхугольник MNLK — параллелограмм.
В переписке с известным целителем и математиком Абу Али ибн Сино Абу Райхон Беруни задаёт следующий вопрос: «Почему Аристотель и другие (философы) называют шесть сторон?»
Рассматривая шестисторонний куб, Беруни говорит о фигурах «с другим количеством сторон» и добавляет, что «шарообразные фигуры не имеют сторон.» А Ибн Сино отвечает, что «во всех случаях нужно считать, что сторон шесть, так как у каждой фигуры, независимо от её формы, есть три измерения — длина, глубина и ширина».
Здесь Ибн Сино имеет ввиду три координаты, именуемые условно «шесть сторон».
В произведении «Канон Масъуда» Беруни приводит точное математическое определение шести сторон: «Сторон шесть, так как они ограничивают движение фигур по своим измерениям. Измерений три: длина, ширина и глубина. А их в два раза больше самих измерений.»
В предыдущих книгах автор определяет положение небесных тел с помощью двух координат относительно небесной сферы — эклиптического уравнения. Либо через те же координаты, но относительно небесного экватора или горизонта. Однако при определении взаимного расположения звёзд и небесных светил придётся учитывать и случаи затмений. Вот в таких случаях появляется необходимость в третьей сферической координате. Эта необходимость привела Беруни к отказу от теории небесных координат.
Векторы в пространстве и действия над ними
Векторы в пространстве
Понятие вектора в пространстве вводят также как на плоскости.
Вектором в пространстве называют направленный отрезок. Основные понятия, относящиеся к векторам в пространстве, аналогичны этим понятиям на плоскости: длина (модуль), направление вектора, равенство векторов.
Координатами вектора с началом в точке А (х1; у1; z1) и концом в точке В (х1; у1; z1) называют числа 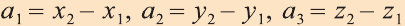
Приведем без доказательства свойства векторов, аналогичных свойствам на плоскости.
Также как на плоскости, соответствующие координаты равных векторов равны и, обратно, векторы с равными координатами равны.
Hа основании этого вектор можно обозначить как 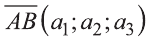
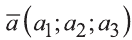
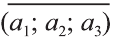
Вектор можно записать и без координат 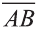
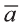
на первом месте начало вектора, а на втором — конец.
Вектор с координатами, равными нулю, называют нулевым вектором и обозначают 
Если начало вектора расположено в начале координат О, а числа а1,
а2 и а3 — координаты точки А, то есть А (а1; а2; а3), то эти же числа будут
координатами вектора 
Однако вектор в пространстве 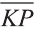
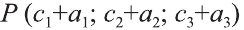
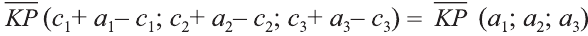
Отсюда следует, что вектор можно приложить к любой точке пространства. В геометрии мы рассматриваем такие свободные векторы. Но в физике, обычно вектор связан с некоторой точкой. Например, воздействие силы приложенная к пружине F на рисунке 19 зависит от точки её приложения.
Длинной вектора называют длину направленного отрезка
изображающего его (рис. 17). Длину вектора 
так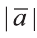
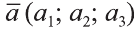
вычисляется по формуле 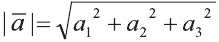
Пример:
Даны точки А (2; 7;-3),В (1; 0; 3), С (-3;-4; 5) и D (-2; 3; -1). Какие из векторов 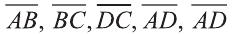
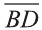
Решение:
У равных векторов равны соответствующие координаты. Поэтому найдём координаты векторов:
Следовательно, 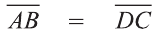
Докажите самостоятельно, что
Действия над векторами в пространстве
Действия над векторами. Сложение векторов, умножение на число и их скалярное произведение определяется также как на плоскости.
Суммой векторов 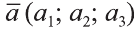

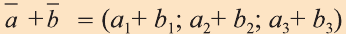
Пусть кран на рисунке 20.b движется вдоль вектора 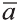
Свойства суммы векторов
Для любых векторов 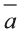
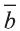
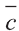
a)
b)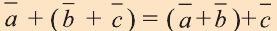
Правило треугольника сложения векторов
Для любых точек А, В и С (рис. 21):
Правило параллелограмма сложения векторов
Если АВСD — параллелограмм (рис. 22), то
Правило многоугольника сложения векторов
Если точки А, В, С, D и Е — вершины многоугольника (рис. 23), то
Правило параллелепипеда сложения трёх векторов, не лежащих в одной плоскости. Если АВСDА1В1С1D1 параллелепипед (рис. 24), то
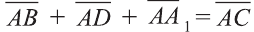
Вектор 




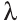
Для любых векторов 

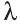
а)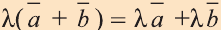
b)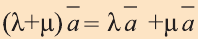
c)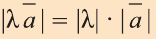
совпадает с направлением вектора 
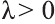
противоположно направлению вектора 
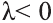
Коллинеарные и компланарные векторы
Пусть заданы ненулевые векторы 
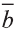


то их называют коллинеарными векторами (рис. 26).
Свойство 1. Если для векторов 

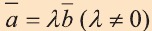
Если 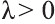



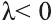
противоположно направлены 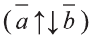
Свойство 2. Если векторы 

то их соответствующие координаты пропорциональны:
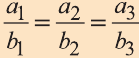
Пример:
Найдите вектор с началом в точке А (1; 1; 1) и концом в точке В, лежащей в плоскости Оху, коллинеарный вектору 
Решение:
Пусть точка В имеет координаты В (х; у; z). Так как точка В лежит в плоскости Оху, то z=0. Тогда 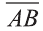
По условию задачи векторы 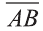

Тогда получаем следующие пропорции 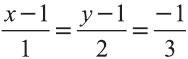
Откуда находим 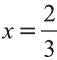
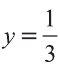
Итак,
Векторы, лежащие в одной плоскости или параллельных плоскостях, называют компланарными векторами (рис. 27).
Векторы 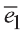
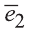
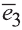
Любой вектор 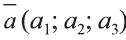
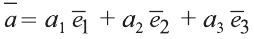
Точно также, если заданы три нeкомпланарных вектора 
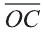
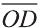
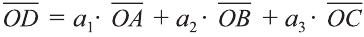
Здесь 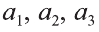
Скалярное произведение векторов
Углом между ненулевыми векторами 

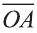

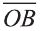

Угол между векторами 

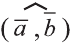
Скалярным произведением векторов 

Если один из векторов нулевой, то скалярное произведение этих векторов равно нулю.
Скалярное произведение обозначают 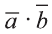
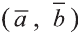
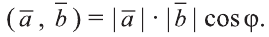
Из определения следует, что если скалярное произведение векторов 

В физике работа A, выполненная при движении тела на расстоянии 
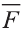
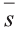
Свойство. Если 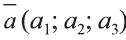


Доказательство. Приложим векторы 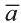

координат О (рис.32). Тогда 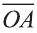
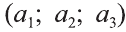
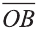
Если векторы неколлинеарны, то получаем треугольник АВО , для которого справедлива теорема косинусов.
Тогда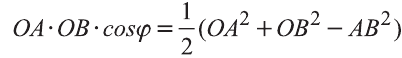
Однако, 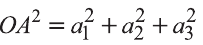
и 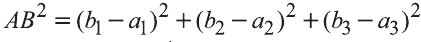
Следовательно,
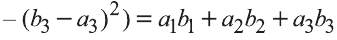
Самостоятельно докажите, что и в случае, когда данные векторы коллинеарны 
это равенство.
Свойства скалярного произведения векторов
1.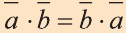
2.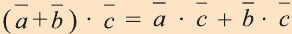
3.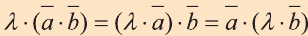
4.Если векторы а и b являются сонаправленными коллинеарными
векторами, то 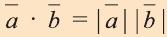
5.Если же векторы противоположно направлены, то 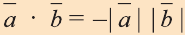
6. 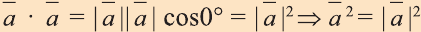
7. Если вектор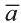

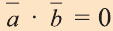
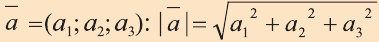
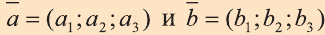
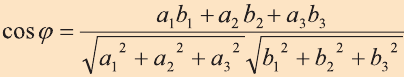
с) условие перпендикулярности векторов 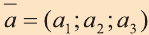
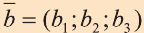
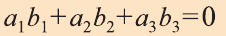
Пример:
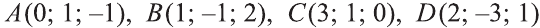
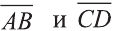
Решение:
Найдём длины векторов 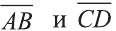
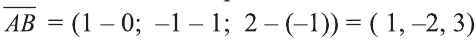
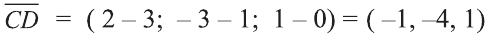
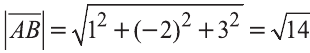
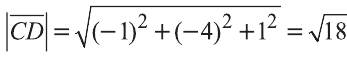
Следовательно,
Пример:
Найдите угол между векторами 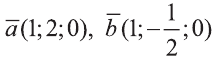
Решение:
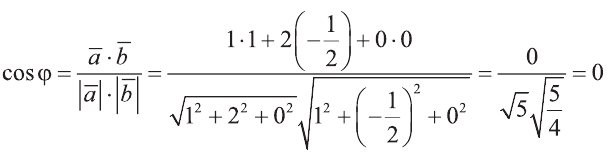
Пример:
Найдите 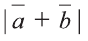
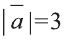
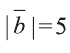


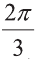
Решение:
Пример:
Найдите координаты и длины векторов 1)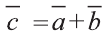
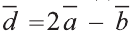
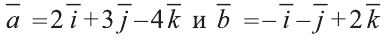
Решение:
Подставим в выражения искомых векторов разложения векторов 

1)
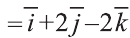
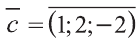
Тогда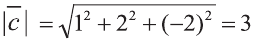
2)
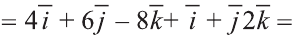
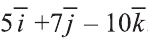
Следовательно, 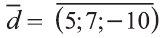
Тогда
- Заказать решение задач по высшей математике
Пример:
Найдите произведение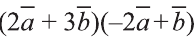


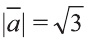
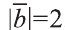
Решение:
Сначала найдём поизведение векторов 

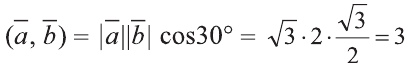
Затем перемножим заданные выражения как многочлены
и, пользуясь распределительным свойством умножения
вектора на число, получим:
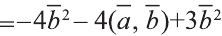
Учитывая, что 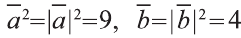
Преобразование и подобие в пространстве
Геометрические преобразования в пространстве
Если каждую точку заданной в пространстве фигуры F изменить одним и тем же способом, то получим фигуру F1. Если при этом преобразовании различные точки первой фигуры переходят в различные точки второй, то говорят о преобразовании геометрической фигуры.
Если рассматривать все пространства как геометрическую фигуру, то также можно говорить о преобразовании геометрической фигуры.
Понятие геометрического преобразование в пространстве вводят также как на плоскости. Следовательно, свойства некоторых рассматриваeмых ниже видов преобразований и их доказательства также подобны соответствующим им на плоскости. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.
Движение и параллельный перенос
Преобразование фигур, при котором сохраняются расстояния между точками, называют движением. Можно привести следующие свойства движения. При движении прямая переходит в прямую, луч — в луч, отрезок — в равный ему отрезок, угол — в равный ему угол, треугольник — в равный ему треугольник, плоскость — в плоскость, тетраэдр — в равный ему тетраэдр.
В пространстве фигуры, которые можно перевести одну в другую при некотором движении называют равными фигурами.
Простейшим примером движения является параллельный перенос.
Пусть в пространстве даны вектор
(рис. 44). Говорят, что точка Х перешла в точку X1 параллельным
переносом на вектор 

Каждая точка подъёмного крана, изображённого на рисунке 46, параллельно перенесена на 40 м относительно начального положения.
Ясно, что параллельный перенос является движением. Поэтому прямая переходит в прямую, луч — в луч, плоскость — в плоскость,
и т. д.
Пусть точка 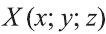
фигуры F1 при помощи параллельного переноса
на вектор 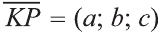
Тогда по определению получим:
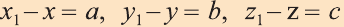
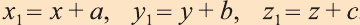
Эти равенства называют формулами параллельного переноса.
Пример:
В какую точку перейдёт точка Р (-2; 4; 6) при параллельном переносе на вектор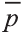
Решение:
По вышеприведённым формулам параллельного переноса: 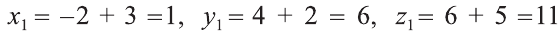
Ответ: 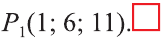
Центральная симметрия в пространстве
Если в пространстве 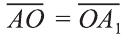
Если в пространстве каждая точка фигуры F переходит в точку, симметричную относительно точки О (рис. 47), то такое преобразование называют симметрией относительно точки О. На рисунках 48, 49 изображёны фигуры симметричные относительно точки О. Симметрия относительно точки является движением.
Если при симметрии относительно точки О фигура F переходит в себя, то её называют центрально симметричной фигурой.
Например, диагонали параллелепипеда (рис. 50) относительно их точки пересечения О являются центрально симметричными фигурами.
Пример:
В какую точку перейдет точка A = (1; 2; 3) при симметрии относительно точки О (2; 4; 6)?
Решение:
Пусть А1 = (х; у; z) — искомая точка. По определению точка
О — середина отрезка АА1. Следовательно,
Из этих уравнений получаем:
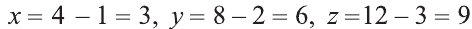
Ответ:
Симметрия относительно плоскости
Точки А и А1 называют симметричными относительно плоскости а,
если плоскость перпендикулярна отрезку и делит его пополам (рис. 51). Фигуры F1, и F2 на рисунке 52 симметричны относительно
плоскости а. Очевидно, что наш силуэт и его отражение симметричны относительно плоскости зеркала (рис. 53).
Симметрия относительно плоскости а является движением.
Поэтому при симметрии относительно плоскости а отрезок переходит в равный ему отрезок, прямая — в прямую, плоскость — в плоскость.
Если при симмeтрии относительно плоскости фигура F переходит в себя, то её называют фигурой симметричной относительно плоскости.
Например, изображённый на рисунке 54 куб, есть фигура, симметричная относительно плоскости а, проходящей через его диагонали АА1 и СС1.
Поворот и симметрия относительно оси
Пусть в пространстве заданы точки А и А1 и прямая l. Если перпендикуляры АК и А1К, опущенные на прямую l, равны и образуют угол 

Если каждую точку фигуры F повернуть на угол 

Поворот относительно прямой также является движением.
Поворот на 180° относительно прямой l называют симметрией относительно прямой l.
Центр, ось и плоскость симметрии называют элементами симметрии. Точки, симметричные точке А (х; у; z) относительно координатных плоскостей, координатных осей и начала координат, будут иметь следующие координаты:
Симметрия в природе и технике
В природе на каждом шагу можно встретить симметрию.
Например, множество живых существ, в частности тела человека и животных, листья растений и цветы устроены симметрично (рис. 58). Также в неживой природе есть элементы, например, снежинки, кристаллы соли. Молекулярное строение веществ тоже состоит из симметричных фигур. Это, конечно, неспроста, поскольку симметричные фигуры не только красивы, но и самые устойчивые.
Раз так, то можно считать, что красота и совершенство природы построены на основе симметрии. Взяв за основу природную красоту и совершенство, строители, инженеры и архитекторы создают строения и механизмы, здания и сооружения, технику и транспортные средства симметричными. В этой работе им очень помогает наука геометрия.
Подобие пространственных фигур
Пусть 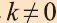
при этом преобразовании для произвольных точек X1 и Х2 фигуры F1 и соответствующих им точек Y1 и Y2 фигуры 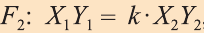
Как видим, понятие преобразования подобия в пространстве вводится также как на плоскости. Следовательно, рассматриваемые ниже виды подобия, их свойства и доказательства этих свойств подобны соответствующим на плоскости. Поэтому, мы не будем останавливаться на их доказательствах и рекомендуем провести их самостоятельно. Преобразование подобия в пространстве отображает прямую в прямую, луч в луч, отрезок в отрезок и угол в угол. Точно также это преобразование плоскость отображает в плоскость.
Если в пространстве одна из фигур перешла в другую с помощью преобразования подобия, то эти фигуры называют подобными.
Пусть в пространстве задана фигура F, точка О и число к 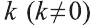
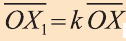


Вы видите, что определение гомотетии в пространстве аналогично соответствующему определению на плоскости. Следовательно, все свойства и их доказательства аналогичны. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.
Гомотетия относительно точки О с коэффициентом 




Если же прямая или плоскость проходят через центр гомотетии, то они отображаются в себя.
- Иррациональные числа
- Действительные числа
- Решение уравнений высших степеней
- Системы неравенств
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
- Уравнение
- Метод математической индукции
I. Механика
Тестирование онлайн
Положение предметов в пространстве. Тело отсчета.
Предлагаю игру: выбрать предмет в комнате и описать его местонахождение. Выполнить это так, чтобы угадывающий не смог ошибиться. Вышло? А что выйдет из описания, если другие тела не использовать? Останутся выражения: «слева от…», «над …» и подобное. Положение тела можно задать только относительно какого-нибудь другого тела.
Местонахождение клада: «Стань у восточного угла крайнего дома села лицом на север и, пройдя 120 шагов, повернись лицом на восток и пройди 200 шагов. В этом месте вырой яму в 10 локтей и найдешь 100 слитков золота». Клад найти невозможно, иначе его давно откопали бы. Почему? Тело, относительно которого совершается описание не определено, неизвестно в каком селе находится тот самый дом. Необходимо точно определиться с телом, которое возьмется за основу нашего будущего описания. Такое тело в физике называется телом отсчета. Его можно выбрать произвольно. Например, попробуйте выбрать два различных тела отсчета и относительно их описать местонахождение компьютера в комнате. Выйдет два непохожих друг на друга описания.
Система координат
Рассмотрим картинку. Где находится дерево, относительно велосипедиста I, велосипедиста II и нас, смотрящих на монитор?
Относительно тела отсчета — велосипедист I — дерево находится справа, относительно тела отсчета — велосипедист II — дерево находится слева, относительно нас оно впереди. Одно и то же тело — дерево, находящееся постоянно в одном и том же месте, одновременно и «слева», и «справа» и «впереди». Проблема не только в том, что выбраны различные тела отсчета. Рассмотрим его расположение относительно велосипедиста I.
На этом рисунке дерево справа от велосипедиста I
На этом рисунке дерево слева от велосипедиста I
Дерево и велосипедист не меняли своего месторасположения в пространстве, однако дерево одновременно может быть «слева» и «справа». Для того, чтобы избавиться от неоднозначности описания самого направления, выберем определенное направление за положительное, противоположное выбранному будет отрицательным. Выбранное направление обозначают осью со стрелкой, стрелка указывает положительное направление. В нашем примере выберем и обозначим два направления. Слева направо (ось, по которой движется велосипедист), и от нас внутрь монитора к дереву — это второе положительное направление. Если первое, выбранное нами направление, обозначить за X, второе — за Y, получим двухмерную систему координат.
Относительно нас велосипедист движется в отрицательном направлении по оси X, дерево находится в положительном направлении по оси Y
Относительно нас велосипедист движется в положительном направлении по оси X, дерево находится в положительном направлении по оси Y
А теперь определите, какой предмет в комнате находится в 2 метрах в положительном направлении по оси X (справа от вас), и в 3 метрах в отрицательном направлении по оси Y (позади вас). (2;-3) — координаты этого тела. Первой цифрой «2» принято обозначать расположение по оси X, вторая цифра «-3» указывает расположение по оси Y. Она отрицательная, потому что по оси Y находится не в стороне дерева, а в противоположной стороне. После того, как выбрано тело отсчета и направления, месторасположение любого предмета будет описано однозначно. Если вы повернетесь спиной к монитору, справа и позади вас будет уже другой предмет, но и координаты у него будут другие (-2;3). Таким образом, координаты точно и однозначно определяют расположение предмета.
Пространство, в котором мы живем, — пространство трех измерений, как говорят, трехмерное пространство. Кроме того, что тело может находится «справа» («слева»), «впереди» («позади»), оно может быть еще «выше» или «ниже» вас. Это третье направление — принято обозначать его осью Z
Можно ли выбирать не такие направления осей? Можно. Но нельзя менять их направления в течение решения, например, одной задачи. Можно ли выбрать другие названия осей? Можно, но вы рискуете тем, что вас не поймут другие, лучше так не поступать. Можно ли поменять местами ось X с осью Y? Можно, но не путайтесь в координатах: (x;y).
При прямолинейном движении тела для определения его положения достаточно одной координатной оси.
Для описания движения на плоскости используется прямоугольная система координат, состоящая из двух взаимно перпендикулярных осей (декартовая система координат).
С помощью трехмерной системы координат можно определить положение тела в пространстве.
Подробнее о системе координат и проекциях
Система отсчета
Каждое тело в любой момент времени занимает определенное положение в пространстве относительно других тел. Определять его положение уже умеем. Если с течением времени положение тела не изменяется, то оно покоится. Если же с течением времени положение тела изменяется, то это означает, что тело движется. Все в мире происходит где-то и когда-то: в пространстве (где?) и во времени (когда?). Если к телу отсчета, системе координат, которые определяют положение тела, добавить способ измерения времени — часы, получим систему отсчета. При помощи которой можно оценить движется или покоится тело.
Относительность движения
Космонавт вышел в открытый космос. В состоянии покоя или движения он находится? Если рассматривать его относительно друга космонавта, находящегося рядом, он будет покоиться. А если относительно наблюдателя на Земле, космонавт движется с огромной скоростью. Аналогично с поездкой в поезде. Относительно людей в поезде вы неподвижно сидите и читаете книгу. Но относительно людей, которые остались дома, вы двигаетесь со скоростью поезда.
Примеры выбора тела отсчета, относительно которого на рисунке а) поезд движется (относительно деревьев), на рисунке б) поезд покоится относительно мальчика.
Сидя в вагоне, ожидаем отправления. В окне наблюдаем за электричкой на параллельном пути. Когда она начинает двигаться, трудно определить кто движется — наш вагон или электричка за окном. Для того, чтобы определиться, необходимо оценить движемся ли мы относительно других неподвижных предметов за окном. Мы оцениваем состояние нашего вагона относительно различных систем отсчета.
Изменение перемещения и скорости в разных системах отсчета
Перемещение и скорость изменяются при переходе из одной системы отсчета в другую.
Скорость человека относительно земли (неподвижной системы отсчета) различная в первом и втором случаях.
Правило сложения скоростей: Скорость тела относительно неподвижной системы отсчета — это векторная сумма скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной.
Аналогично вектора перемещения. Правило сложения перемещений: Перемещение тела относительно неподвижной системы отсчета — это векторная сумма перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной.
Пусть человек идет по вагону по направлению (или против) движения поезда. Человек — тело. Земля — неподвижная система отсчета. Вагон — подвижная система отсчета.
|
Вектора подвижной со и тела относительно подвижной со совпадают по направлению |
Вектора подвижной со и тела относительно подвижной со противоположные по направлению |
Изменение траектории в разных системах отсчета
Траектория движения тела относительна. Например, рассмотрим пропеллер вертолета, спускающегося на Землю. Точка на пропеллере описывает окружность в системе отсчета, связанного с вертолетом. Траектория движения этой точки в системе отсчета, связанной с Землей, представляет собой винтовую линию.
Поступательное движение
Движение тела — это изменение его положения в пространстве относительно других тел с течением времени. Каждое тело имеет определенные размеры, иногда разные точки тела находятся в разных местах пространства. Как же определить положение всех точек тела?
НО! Иногда нет необходимости указывать положение каждой точки тела. Рассмотрим подобные случаи. Например, это не нужно делать, когда все точки тела движутся одинаково.
Одинаково движутся все токи чемодана, машины.
Движение тела, при котором все его точки движутся одинаково, называется поступательным
Материальная точка
Не нужно описывать движение каждой точки тела и тогда, когда его размеры очень малы по сравнению с расстоянием, которое оно проходит. Например, корабль, преодолевающий океан. Астрономы при описании движения планет и небесных тел друг относительно друга не учитывают их размеров и их собственное движение. Несмотря на то, что, например, Земля громадная, относительно расстояния до Солнца она ничтожно мала.
Нет необходимости рассматривать движение каждой точки тела, когда они не влияют на движение тела всего целиком. Такое тело можно представлять точкой. Все вещество тела как бы сосредотачиваем в точку. Получаем модель тела, без размеров, но она имеет массу. Это и есть материальная точка.
Одно и то же тело при одних его движениях можно считать материальной точкой, при других — нельзя. Например, когда мальчик идет из дома в школу и при этом проходит расстояние 1 км, то в этом движении его можно считать материальной точкой. Но когда тот же мальчик выполняет зарядку, то точкой его считать уже нельзя.
Рассмотрим движущихся спортсменов
В этом случае можно спортсмена моделировать материальной точкой
В случае прыжка спортсмена в воду (рисунок справа) нельзя моделировать его в точку, так как от любого положения рук и ног зависит движение всего тела
Главное запомнить
1) Положение тела в пространстве определяется относительно тела отсчета;
2) Необходимо задать оси (их направления), т.е. систему координат, которая определяет координаты тела;
3) Движение тела определяется относительно системы отсчета;
4) В разных системах отсчета скорость тела может быть разной;
5) Что такое материальная точка
Видеодемонстрация относительности движения
Сложение скоростей
Упражнения
Мимо стоящего велосипедиста проезжает колонна движущихся с одинаковой скоростью машин. Движется ли каждая из машин относительно велосипедиста? Движется ли машина относительно другой машин? Движется ли велосипедист относительно машины?
Из центра горизонтально расположенного вращающегося диска по его поверхности пущен шарик. Каковы траектории шарика относительно Земли и диска?
Чему равно перемещение какой-либо точки, находящейся на краю диска радиусом R при его повороте относительно подставки на 600? на 1800? Решить в системах отсчета, связанных с подставкой и диском.
Почему дождевые капли в безветренную погоду оставляют наклонные прямые полосы на стеклах равномерно движущегося поезда?
Каким образом можно определить скорость бега, если тренироваться на беговой дорожке со сломанным автоматическим определением скорости? Ведь относительно стен зала не пробегаешь ни одного метра.
Эскалатор метро движется вверх со скоростью 0,75 м/с. а) С какой скоростью и в каком направлении надо идти по эскалатору, чтобы быть все время на уровне одного из фонарей освещения туннеля? б) С какой скоростью относительно поднимающейся лестницы надо было бы передвигаться, чтобы опускаться вниз со скоростью пассажиров, неподвижно стоящих на другой опускающейся лестнице?
Какую систему координат следует выбрать (одномерную, двухмерную, трехмерную) для определения положения таких тел:
1. трактор в поле;
2. поезд;
3. люстра в комнате;
4. лифт;
5. подводная лодка;
6. шахматная фигура
Положение тела
или точки можно задать только относительно
какого-нибудь другого тела, которое
называют телом
отсчета.
Тело отсчета можно выбрать произвольно.
Им может быть дом, в котором мы живем,
вагон поезда, в котором мы едем, и т.д.
Телами отсчета могут служить тела,
звезды, Земля, Солнце.
Когда тело отсчета
выбрано, через какую-нибудь его точку
проводят оси координат, и положение
любой точки в пространстве описывают
ее координатами.
Для определения
положения тела в пространстве используется
система координат.
При прямолинейном
движении тела для определения его
положения достаточно одной координатной
оси. Например, если автомобиль движется
по прямой дороге, то его движение
описывается одной координатой.
Для описания
движения на плоскости используется
прямоугольная система из двух взаимно
перпендикулярных осей, такая система
еще называется декартовой
системой координат. Например,
когда автомобиль едет из одного города
в другой, то его движение, как правило,
является криволинейным и описывается
двумя координатами.
Движение тела в
поле тяжести Земли нельзя описать двумя
координатами. В этом случае используют
трехмерную систему координат, с помощью
которой можно определить положение
тела в пространстве.
Итак, положение
точки на линии, плоскости и в пространстве
определяют соответственно одним, двумя
или тремя числами – координатами.
Пространство, в котором мы живем, —
пространство трех измерений, трехмерное
пространство.
Но если необходимо
определить путь, который прошло тело
за определенный промежуток времени, то
нам потребуется еще приборы для измерения
времени – часы. Система
координат,
связанная с телом
отсчета, и
часы
для отсчета времени образуют систему
отсчета,
позволяющую определять положение
движущегося тела в любой момент времени.
1.4 Перемещение
В процессе
механического движения положение тела
в пространстве изменяется. Раньше мы
использовали понятие пути
– длины траектории, пройденной телом
за время наблюдения.
Путь обозначают буквой
l,
единицей пути в СИ является метр (1м).
Путь является величиной скалярной,
т.е. не имеющей направления.
Однако для решения
практических задач недостаточно задать
только путь. Например, из лыжной базы в
15 км к северу от города вышел лыжник и
за 2 ч прошел 15 км. Как определить куда
он пришел? Он мог дойти до города – путь
Б, а мог и вернуться обратно – путь А. В
любом случае путь будет равен 15 км, но
положение в пространстве будет разным.
Чтобы избежать
такой неопределенности, вводиться
понятие перемещения.
Перемещение – направленный отрезок,
соединяющий начальное и конечное
положение тела.
Таким образом, перемещение – величина
векторная, то есть имеющая направление.
Перемещение обозначается символом
, единицей перемещения, как пути, является
метр.
В том случае, когда
вектор перемещения лыжника был направлен
на юг, то модуль перемещения равен 15 км,
и мы можем сказать, что лыжник дошел до
города. А в случае, когда лыжник пришел
обратно на базу, его перемещение равно
нулю.
Изменение положения
тела в пространстве можно изобразить
графически, используя понятие перемещения.
Однако в большинстве случаев необходимо
вычислить
положение этого тела, то есть определить
его координаты. При этом вычисления
проводят не с координатами векторов
как таковыми, а с их проекциями
на оси координат и модулями
векторов,
то есть с величинами, представляющими
собой положительные или отрицательные
числа.
Особенно важен
частный случай проектирования вектора
на два взаимноперпендикулярных
направления. Здесь (x0,y0)
и (x,
y)
— координаты начала и конца вектора.
Проекция вектора
равна разности координат конца и начала
вектора:
Sx
= x
– x0
Sy
= y
– y0
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Материал из PhysBook
Перейти к: навигация, поиск
Содержание книги
Следующая страница
Содержание
-
1 Описание положения тела в пространстве
- 1.1 Декартовые координаты точки в пространстве
- 1.2 Преобразования координат
- 1.3 Относительные и инвариантные величины
- 1.4 Материальная точка
- 1.5 Абсолютно твердое тело
- 1.6 Число степеней свободы тела
- 1.7 Существует ли четвертое измерение?
- 1.8 Механическое движение. Закон движения
- 2 Примечания
Описание положения тела в пространстве
Декартовые координаты точки в пространстве
Положение (место) точки в пространстве математически удобно описывать с помощью чисел – координат. Простейшей системой (и хорошо вам знакомой) координат является прямоугольная декартовая система. Для ее построения необходимо задать (см. рис.1):
- Начало отсчета – произвольную точку O;
- Направления трех взаимно перпендикулярных осей координат, традиционно обозначаемых (X, Y, Z);
- Единицу измерения длины (отрезок единичной, по определению, длины).
Для определения координат точки A необходимо опустить перпендикуляры из точки A на оси координат (спроецировать точку на оси координат) и задать координаты точек-проекций (x,y,z). Каждое число-координата имеет следующий смысл: декартовой координатой точки на прямой является число, модуль которого равен расстоянию до начала отсчета, а знак указывает, с какой стороны от начала отсчета находится данная точка.
Так как координата точки указывает расстояние до начала отсчета, то ее размерность — размерность длины.
Рассмотрим теперь эти известные математические положения с физической точки зрения. Пространство, в котором мы живем, не имеет «выделенных» точек и направлений, с которыми раз и навсегда можно связать единую и абсолютную систему отсчета. Поэтому положение данного тела можно определить только относительно других тел. В связи с этим начало отсчета физической системы координат удобно связывать с некоторым конкретным телом (которое называется тело отсчета). Направления осей координат также следует связывать с другими материальными телами. В качестве единицы длины используются эталоны, которые воспроизводятся с помощью физических приборов. В международной системе единиц СИ единицей длины является метр.
Подчеркнем, что выбор всех элементов системы координат, в принципе, является произвольным, следовательно, координаты точки относительны. Иными словами, числа-координаты имеют смысл только в том случае, если задана система координат, то есть положение данного тела определяется относительно других тел, с которыми связана система координат.
Во многих случаях задание трех координат точки является излишним. Так если тело движется вдоль заданной (известной) прямой, то имеет смысл одну из осей (скажем X) направить вдоль этой прямой. Тогда оставшиеся координаты (y,z) все время будут равны нулю, поэтому их можно не принимать во внимание.
Заметим, что аналогичным образом можно ввести координаты точки на произвольной заданной линии, измеряя длину участка этой линии между данной точкой и началом отсчета и указывая с помощью знаков с какой стороны от начала отсчета находится точка.
Аналогично, при движении тела по заданной плоскости (и даже произвольной поверхности), достаточно определить в этой плоскости две оси координат.
Эквивалентным координатному является векторный способ описания положения.
В рамках этого метода положение точки в пространстве задается с помощью радиус-вектора 
Преобразования координат
Как уже было отмечено, координаты точки относительны, они изменяются при переходе в другую систему координат. Во многих случаях, требуется перейти из одной системы координат в другую. Получим формулы таких преобразований для одного частного случая – сдвига начала отсчета на плоскости. Пусть на известной плоскости заданы две декартовые системы координат XOY (которую условно назовем «исходной») и X’O’Y’ (назовем ее «сдвинутой»), оси которых параллельны (см. рис.2). Обозначим (x0,y0) координаты начала отсчета сдвинутой системы в исходной системе.
Как следует из рис. 2, координаты точки A в сдвинутой и исходной системах связаны очевидными соотношениями (прямые)

обратные:

Какую из этих систем считать исходной, а какую сдвинутой, безразлично – системы полностью равноправны. Заметьте, что обратные преобразования могут быть получены заменой (x0,y0) на (-x0,-y0) . Последняя пара чисел является координатами начала отсчет исходной системы в сдвинутой.
Эти же преобразования короче могут быть записаны и в векторной форме (рис. 3)

Аналогичные преобразования при параллельном сдвиге начала отсчета могут быть получены и в трехмерном случае. Более сложный вид имеют формулы преобразования координат при повороте осей (в нашем изложении они нам не понадобятся, поэтому приводить их не будем). Важно, что в любом случае можно найти формулы, позволяющие переходить из одной системы координат в другую. Это обстоятельство, указывает, что произвол в выборе системы координат не вносит существенных трудностей в описание движения тел.
Относительные и инвариантные величины
Мы показали, что при переходе из одной системы в другую координаты точки изменяются (координаты относительны). Помимо относительных величин (зависящих от системы координат) имеются величины независящие от системы координат (такие величины называются инвариантными). Примером такой величины является расстояние между двумя точками. Действительно, пусть на плоскости (рис.4) расположены две точки: A1 с координатами (x1,y1) и A2 с координатами (x2,y2).
Тогда на основании теоремы Пифагора расстояние между точками может быть вычислено по формуле

При переходе в любую другую систему отсчета (при неизменной единице длины) расстояние, вычисленное по формуле (4), остается неизменным. Например, при сдвиге начала отсчета, описываемом уравнениями (1), все четыре координаты изменятся, но разности одноименных координат, а, следовательно, и расстояние останутся неизменными (инвариантными). Можно указать и другие геометрические инвариантные величины – углы между отрезками, площади и объемы фигур и др. Особенно отметим, что соотношения, записанные в векторной форме, остаются неизменными при преобразованиях координат. Так, например, скалярное произведение[1] двух векторов не зависит от выбора системы координат. В частном случае, скалярное произведение вектора на самого себя равно квадрату длины вектора. Поэтому формула (4) в векторной форме имеет вид

Поиск инвариантных величин, не изменяющихся при преобразованиях координат, представляет большой интерес, а многие физические теории и формулируются в терминах инвариантных величин.
Задание для самостоятельной работы
1. В полярной системе координат положение точки A на плоскости задается с помощью а) расстояния r до начала координат O, б) угла φ, который образует отрезок OA с осью X.
Установите связь между полярными (r,φ) и декартовыми координатами точки.
Выразите расстояние между двумя точками через их полярные координаты.
Обсуждая вопрос об описании положения тела в пространстве, мы стыдливо умолчали о том, что не определили понятия «тело». Фактически речь шла о геометрических точках пространства. Любой реальный объект имеет конечные геометрические размеры и определенную форму. Кроме того, реальные тела обладают множеством иных характеристик — массой, температурой, цветом и так далее. Полностью описать все свойства реальных тел, все физические процессы в рассматриваемых телах невозможно из-за их бесконечного многообразия. Поэтому, рассматривая те или иные явления необходимо отвлечься, «забыть» на время, пренебречь некоторыми характеристиками тел и явлений, иными словами, построить модель явления, модель тела. Какими свойствами тела можно в данных условиях пренебречь зависит от конкретной физической задачи, конкретной цели физического исследования.
Материальная точка
Во многих кинематических задачах оказывается возможным пренебречь размерами самого тела. Еще раз рассмотрим автомобиль, движущийся из Минска в Брест. Расстояние между этими городами порядка 350 километров, размеры автомобиля — несколько метров, поэтому в такой ситуации при описании положения автомобиля можно не учитывать его размеры — если капот автомобиля находится в Бресте у нужного подъезда нужного дома, то можно считать, что и его багажник находится приблизительно там же. Таким образом, в данной задаче можно мысленно заменить автомобиль его моделью — телом, размеры которого пренебрежимо малы. Такая модель тела очень часто используется в физике и называется материальной точкой.
Материальная точка — это идеальная модель тела, размерами которого в данных условиях можно пренебречь.
Общим у геометрической и материальной точек является отсутствие собственных размеров. Материальную точку, по мере необходимости, можно «наделять» свойствами, которыми обладают реальные тела, например, массой, энергией, электрическим зарядом и так далее.
Одним из критериев применимости модели материальной точки является малость размеров тела по сравнению с расстоянием, на которое оно перемещается. Однако это условие не является абсолютно однозначным. Так, описывая движение Земли вокруг Солнца при расчете ее положения на орбите, размерами Земли можно пренебречь, считать ее материальной точкой. Однако, если нам необходимо рассчитать времена восхода и заката Солнца, модель материальной точки принципиально неприменима, так как это описание требует учета вращения Земли, учета ее размеров и формы.
Рассмотрим еще один пример. Спринтеры соревнуются на стометровой дистанции. Цель описания движения – выявить, кто из спортсменов пробегает дистанцию за меньшее время (задача чисто кинематическая). Можно ли в данной задаче считать бегуна материальной точкой? Его размеры значительно меньше дистанции забега, но достаточно ли они малы, чтобы ими можно было пренебречь? Ответ на эти вопросы зависит от требуемой точности описания. Так, на серьезных соревнованиях время измеряется с точностью 0.01 секунды, за это время бегун смещается на расстояние порядка 10 сантиметров (простая оценка, полученная исходя из средней скорости спринтера 10м/с). Следовательно, погрешность, с которой определяется положением бегуна (10 см) меньше, чем его поперечные размеры, поэтому модель материальной точки в данном случае неприменима. Не случайно мастера спринтерского бега на финише «бросают грудь вперед», выигрывая драгоценные сотые доли секунды. Таким образом, вторым критерием применимости модели является требуемая точность описания физического явления.
В некоторых ситуациях можно использовать модель материальной точки, даже если размеры тела сравнимы и даже больше расстояний, на которое смещается тело. Это допустимо тогда, когда положение одной точки тела однозначно определяет положение всего тела. Так при скольжении бруска по наклонной плоскости, зная положение его центра (как, впрочем, и любой другой точки) можно найти положение всего тела. Если модель материальной точки оказывается неприменимой, то необходимо использовать другие более сложные модели.
Абсолютно твердое тело
Многие реальные тела являются твердыми, то есть в течении длительного времени сохраняют свои размеры и форму, точнее говоря изменения размеров и формы настолько незначительны, что ими можно пренебречь. Моделью таких тел служит абсолютно твердое тело.
Абсолютно твердое тело — это идеальная модель тела, изменением размеров и формы которого в данных условиях можно пренебречь.
Из этого определения следует, что расстояния между двумя любыми точками абсолютно твердого тела остается неизменным. Абсолютно твердое тело можно также рассматривать как совокупность материальных точек, жестко связанных между собой. Так положение океанского лайнера в открытом море можно описать, пользуясь моделью материальной точки, а его пространственную ориентацию (курс, наклон) с помощью модели абсолютно твердого тела. Применимость модели абсолютно твердого тела обусловлена только конкретной исследуемой проблемой — целью моделирования и требуемой точностью.
Число степеней свободы тела
Теперь, после того как мы изучили несколько моделей тел, можно окончательно и корректно сформулировать ответ на вопрос: «Что означает задать, определить положение тела?» — Указать численной значение координат некоторых точек тела так, чтобы положение всего тела (любой его части) было определено однозначно.
Число независимых координат, которые однозначно определяют положение тела или системы тел в пространстве называется числом степеней свободы.
Число степеней свободы очень важная характеристика описываемой системы, хотя бы потому, что определяет число независимых уравнений, описывающих движение системы.
Подсчитаем число степеней свободы некоторых простых систем.
Материальная точка, по определению, не имеет размеров, поэтому ее положение в пространстве определяется однозначно тремя координатами. Следовательно, число степеней свободы свободно материальной точки равно трем. Если на движение материальной точки накладываются дополнительные условия, то число ее степеней свободы может уменьшиться. Так если точка движется по заданной поверхности, то ее положение определяется двумя независимыми координатами, следовательно, число степеней свободы равно двум; при движении по заданной линии число степеней свободы уменьшается до одной. Подчеркнем, это не значит, что при движении по заданной линии может изменяться только одна и — могут изменяться все три, но положение точки на заданной линии определяется одной координатой, и если она известна, то могут быть определены и две других. Тем не менее, описание положения точки на заданной линии с помощью одной координаты оказывается не всегда удобным. Ценность рассмотренных нами декартовых координат в том, что они позволяют установить физические законы, описывающее движение вдоль всех прямых (все прямые одинаковы!). В то же время, для описания изменения координат на произвольной линии пришлось бы записывать свои законы для каждой линии — окружности, параболы, синусоиды и т.д. Поэтому часто одномерное движение вдоль известной линии описывают с помощью двух или трех координат. Однако и в этом случае число степеней свободы остается равным единице.
Если механическая система может быть промоделирована как N материальных точек, движущихся в пространстве, то, очевидно, полное число ее степеней свободы равняется 3N. Но если на движение этих материальных точек накладываются дополнительные ограничения, то число степеней свободы уменьшается.
Рассмотрим, как можно описать положение в пространстве двух материальных точек жестко связанных между собой (что-то похожее на гантели). Две точки имеют шесть степеней свободы, которые могут быть описаны шестью координатами — x1, y1, z1, x2, y2, z2, но так как расстояние между точками неизменно, то на эти координаты накладывается условие

где l — расстояние между точками, поэтому число независимых координат, или число степеней свободы равно пяти.
Таким образом, число степеней свободы системы, состоящей из N материальных точек равно 3N минус число дополнительных условий (связей), накладываемых на движение этих точек.
Число степеней свободы может быть подсчитано и другим способом. Обратим внимание, что точное определение координат уменьшает «подвижность» точки (или системы точек). Так, например, если для материальной точки задана координата z, то точка может двигаться только в плоскости перпендикулярной оси Z, задание еще одно координаты (скажем y), приводит к тому, что точка может двигаться только вдоль прямой параллельной оси X. Поэтому число степеней свободы можно находить, подсчитывая, сколько независимых координат необходимо определить, чтобы жестко «закрепить» тело. С помощью такого подхода найдем число степеней свободы системы, состоящей из двух жестко связанных точек. Задавая три координаты одной точки, мы ее как бы закрепляем, тогда вторая точка сможет двигаться так, что бы ее расстояние до первой оставалось неизменным, то есть по поверхности сферы радиуса l. Понятно, что если определено положение двух точек твердого тонкого стержня, то задано и положение всего стержня, поэтому тонкий стержень имеет пять степеней свободы.
Посчитаем число степеней свободы свободно движущегося абсолютно твердого тела. Выберем внутри тела три произвольных точки A, B, C, не лежащих на одной прямой. (рис 5). Положение одной точки A, определяется тремя координатами, если задано положение точки A, то положение точки B может быть описано двумя координатами. Наконец, при «закрепленных» точках A и B, тело может только вращаться вокруг оси, проходящей через эти точки. Следовательно, точка C имеет одну степень свободы. Таким образом, абсолютно твердое тело имеет шесть степеней свободы.
Как мы уже отмечали, для описания положения точки можно использовать разные системы координат, аналогично, положение твердого тела также может быть описано различными способами, только число независимых координат во всех способах описания будет одним и тем же равным числу степеней свободы. Так во многих случаях, положение твердого тела, описывают, задавая три декартовые координаты одной из его точек (чаще центра), и три угла, определяющие его ориентацию.
Существует ли четвертое измерение?
В научно-фантастических произведения иногда встречаются сюжеты, в которых разумные существа осваивают четвертое, пятое и так далее измерения [2]. Повышение размерности пространства предоставляет новые богатейшие возможности, как для этих существ, так и для писателей-фантастов. Сравните двухмерную плоскость и трехмерное пространство! Для того чтобы «выйти» из плоскости в трехмерное пространство можно предложить следующий метод: из центра окружности необходимо провести бесконечный луч, который нигде не пересекает окружность, такой луч лежит в третьем измерении. По аналогии можно предложить «путь в четвертое измерение»: из центра сферы необходимо провести луч, который нигде не пересекает сферу — вообразили? Еще один способ — провести прямую, которая перпендикулярна трем взаимно перпендикулярным прямым. Конечно, если вам не удалось представить себе такой луч или такую прямую, то это еще не является доказательством отсутствия четвертого измерения в нашем пространстве.
Попытаемся представить, к каким наблюдаемым явлениям могло бы привести наличие дополнительного измерения. Например, «из четвертого измерения» можно было бы заглянуть внутрь любого трехмерного тела (как из третьего измерения можно видеть «внутренности» любой плоской фигуры). Далее, был бы возможен бесследный «уход» и обратное появление в любом другом месте любых материальных тел (опять же представьте себе, что будет происходить на плоскости, которую пересекает трехмерное тело). К настоящему времени таких фактов не зафиксировано. Более того, не известно таких явлений, которые не могли бы быть объяснены с точки зрения пространства трех измерений.
Еще одним доказательством трехмерности пространства, в котором мы обитаем, является ряд физических законов. Рассмотрим, например, точечный источник, который посылает свет во все стороны равномерно. Понятно, что энергия, пересекающая поверхность любой сферы, внутри которой находится источник, должна быть постоянна. Следовательно, интенсивность света (то есть энергия, приходящаяся на единицу площади) должна убывать обратно пропорционально площади сферы, то есть обратно пропорционально квадрату расстояния. Если бы свет распространялся и в четвертом измерении, то его интенсивность убывала бы обратно пропорционально кубу расстояния. Эксперимент однозначно утверждает, что интенсивность убывает обратно пропорционально квадрату расстояния. Эти и другие факты утверждают, что наше пространство действительно трехмерно. Таким образом, ответ на вопрос этого раздела в настоящее время следующий:
Пространство четырех и более измерений является математической абстракцией, можно изучать свойства геометрических объектов в таких пространствах, при решении целого ряда задач, в том числе физических бывает полезно их рассматривать в многомерных пространствах, однако, в настоящее время нет никаких оснований полагать, что реально существует четвертое измерение в том смысле, что реально существуют некоторые материальные тела вне пространства трех измерений.
Вопросы для самостоятельной работы.
- Подсчитайте число степеней свободы тонкого стержня, толщиной которого можно пренебречь.
- Две материальные точки связаны пружиной. Чему равно число степеней свободы такой системы?
- Чему равно число степеней свободы руки человека?
Механическое движение. Закон движения
Окружающий нас мир не является застывшим, в нем постоянно происходят всевозможные изменения — «все течет, все изменяется», и нет необходимости убеждать кого-либо в этой очевидной истине. Простейшим видом изменений, происходящих в окружающем нас мире, является изменение положений тел в пространстве, механическое движение.
Механическим движением называется изменение положений тел в пространстве с течением времени.
При движении материальной точки она описывает в пространстве некоторую линию. Для описания движения можно попытаться найти эту линию, а затем описывать положение точки на этой ней. Для этого можно, например, задать зависимость пройденного пути от времени движения.
Линия, вдоль которой движется материальная точка, называется траекторией движения.
Путь, пройденный точкой равен длине участка траектории между двумя последовательными положениями тела.
Однако определение траектории движения часто представляет собой отдельную и достаточно сложную задачу, поэтому часто оказывается более простым и удобным описывать механическое движение иным способом.
Мы уже знаем, что положение тела в пространстве описывается с помощью координат. Если положение тела изменяется, то изменяются и его координаты, они становятся зависящими от времени, становятся функциями времени.
Зависимость всех координат тела от времени называется законом движения.
Таким образом, закон движения определяет положение тела в любой произвольный момент времени. Математическим выражением закона движения является набор функций — зависимостей координат от времени. Таким образом, нам необходимо дополнить рассмотренную систему координат прибором для измерения времени — часами. Дальше такой набор — системы координат и часов мы будем называть системой отсчета. Как всякая функция закон движения может быть представлен в нескольких формах — в виде таблицы, в виде графика, в виде формулы.
Подчеркнем, что закон движения полностью описывает движение, дает исчерпывающую информацию о движении, зная его можно найти любую характеристику движения. Однако, задача физики, заключается не только в том чтобы просто описать наблюдаемое движение, более важная задача — научиться предсказывать движение, рассчитывать его, строить его модели, создавать условия, для того чтобы получить движение требуемого вида. Для успешного решения таких проблем нам необходимо ввести и изучить некоторые характеристики механического движения (скорость, ускорение и т.д.), которые позволяют теоретически находить законы движения.
Примечания
- ↑ Напомним, результатом скалярного произведения двух векторов
и
называется число c , равное произведению модулей векторов на косинус угла α между ними:
.
- ↑ Для примера можно вспомнить знаменитый роман М.Булгакова «Мастер и Маргарита»
Смотреть HD
видео онлайн
бесплатно 2022 года
Физика. Кинематика
Равноускоренное движение по прямой и под углом к горизонту
Как определить положение тела в пространстве? И для чего нужны координаты?
Школьный курс физики начинается с раздела кинематика. Именно она закладывает фундамент для дальнейшего изучения, все остальные разделы так или иначе будут соприкасаться с этим разделом.
Что же такое кинематика? Это раздел физики, который изучает движение некоторого тела в пространстве. При это мы НЕ рассматриваем, что вызывает это движение, что является его причиной. У нас просто есть какое-то двигающееся тело и мы пытаемся его изучить. А на вопрос почему происходит движение, кинематика нам ответа не дает, это мы будем изучать в следующих разделах физики.
Начнем с простого вопроса – что такое «тело»? Это может быть все, что угодно – машина, самолет, мячик, капля воды, планета и т.д., то есть любой движущийся объект. Любое тело в школьной физике мы будем представлять в виде материальной точки.
Определение. Материальная точка – это тело, размерами которого мы можем пренебречь в данной задаче.
Мы просто договариваемся, что любой объект, будь то ракета или песчинка с пляжа, мы представляем в виде точки. Это необходимо для того, чтобы размеры тела не оказывали влияния на наши задачи. Так, например, автобус, двигающийся из Москвы в Санкт-Петербург, можно считать материальной точкой. Его размеры очень малы по сравнению с расстоянием между этими городами. Но движение пассажиров при выходе из автобуса уже нельзя считать материальной точкой, потому что пассажиры относительно автобуса не такие уж и маленькие. Такое школьное допущение (а в физике допущений будет много) упростит нам жизнь. При более глубоком изучении физики вы будете учитывать все эти допущения, в том числе и размеры тела, но в школе вам это, как правило, не нужно.
Задача кинематики – предсказать или описать при помощи законов физики, как этот объект будет двигаться в будущем, например, через час, если ничего не изменится.
Зачем нам это? Очень просто: если мы знаем, по каким законам двигается машина, мы легко сможем предсказать будущее и узнать, где она будет через какое-то время и с какой скоростью будет двигаться. Естественно, мы можем точно так же предсказывать движение брошенного камня и любых других объектов. Например, зная начальную скорость камня и как вы его кинули, можно предсказать, как далеко или высоко он улетит, или через сколько времени и с какой скоростью он упадет на землю.
Траектория, путь и перемещение. Что это такое и чем они отличаются?
Перед тем, как писать формулы, познакомимся еще с несколькими определениями, которые нам понадобятся в дальнейшем. Представим, что человек идет из пункта (А) в пункт (В) (см Рис.1.).
Рис.1. Траектория (зеленая линия). Путь(длина зеленой линии). Перемещение(фиолетовая стрелка)
- Траектория – линия, вдоль которой движется тело. На рис.1 показана зеленой линией.
- Путь – длина траектории. Обычно обозначается буквой (S).
- Перемещение – вектор, соединяющий начальную и конечную точки (фиолетовая линия). О том, что такое вектор, мы поговорим чуть позже. А на нашем рисунке перемещение — это длина отрезка (АВ), кроме длины перемещение еще показывает куда движется тело из начальной точки (А) в конечную (В).
Разберемся подробнее на примере. Если вы ходите по комнате с шагомером туда-сюда и вернетесь в итоге в исходную точку, то ваше перемещение будет равно 0, а путь будет расстоянием, которое вы находили, его покажет шагомер.
Что такое координаты и зачем они нужны?
Все это звучит здорово, но как нам определить положение тела в пространстве? Для этого люди придумали очень удобную штуку, которая называется координатная плоскость. С этим понятием вы должны были сталкиваться в курсе алгебры – построение графиков в осях (х) и (y). Помните, у вас были функции типа (y=x^2-3) и нужно было построить график этой функции по точкам? Вы брали какие-то значения (x) подставляли в (y=x^2-3) и получали значение (y). Потом отмечали получившуюся точку на координатной плоскости. Именно эта плоскость нас и будет интересовать.
Координаты используются людьми повсюду. Например, вся поверхность Земли расчерчена линиями, которые называются долгота и широта. Этих линий очень много, но указав пересечение некоторой долготы (37) с какой-то широтой (55), я укажу вполне конкретную точку на земной поверхности – это примерное расположение города Москва (37;55). Именно такой способ используется для определения положения любого объекта на Земле в географических картах и навигаторах – город, озеро, здание, машина, человек и т.д.
Для начала давайте рассмотрим одномерное движение – это такое движение, при котором машина может двигаться только вперед по дороге или назад, никуда свернуть она не может. (Рис.2.). Наложим на нашу дорогу ось Х, направленную вправо, как на рисунке. Теперь вся наша дорога размечена координатами. И мы можем определить положение машины, просто сказав ее координату. Начало координат мы можем выбрать как угодно, пусть оно будет в точке О. Тогда на рисунке наша машина находится в начальной координате (x_0=3). Из этой точки она может поехать влево (координата будет уменьшаться) или вправо (координата будет увеличиваться).
Расстояние можно измерять в различных единицах измерения: километры, метры, сантиметры, миллиметры и т.д. Пусть все координаты у нас измеряются в метрах, тогда можно сказать, что на рисунке машина находится на расстоянии 3 метра от точки О.
Итак, мы научились определять положение тела в пространстве при помощи координат.
Что такое скорость?
На интуитивном уровне это понятно. Но давайте попробуем вникнуть поглубже. В чем всегда измеряется скорость? В автомобиле это обычно километры в час (км/ч), измеряется при помощи спидометра. То есть спидометр машины показывает, сколько километров проедет машина за один час, если не будет менять скорость. Точно так же скорость можно измерять в метрах в секунду (м/с), километрах в секунду (км/с) и т.д. Значит, если я умножу скорость на количество часов, которые едет машина с этой скоростью, то получу расстояние, пройденное машиной за это время. Можно записать в виде известной формулы движения с постоянной скоростью:
$$S=V*t;$$
Итак, при движении с постоянной скоростью (V), можно посчитать расстояние (S), которое проходит тело за время (t).
Теперь давайте предположим, что машина двигается с постоянной скоростью 1 (м/с) влево из начальной точки с координатой (x_0=3(м)). Это означает, что машина за 1 секунду сдвинется на (S=V*t=1*1=1(м)) метр влево, то есть окажется в точке с координатой (2) (м). Через 2 секунды она пройдет расстояние (S=V*t=1*2=2(м)) и попадет в координату (1)(м), а через 6 секунд на (S=V*t=1*6=6(м)) и окажется в координате (-3)(м).
Скорость кроме величины еще имеет направление – в нашем случае это означает, что если машина едет вправо (туда же, куда направлена ось (х)), то скорость будет положительна, а если влево (в противоположную сторону направлению оси (х)), то скорость будет отрицательна.
Все, что имеет величину и направление, называется вектором. То есть скорость ни что иное, как вектор. Вектор – это ключевое понятие физики. Мы часто будем сталкиваться с величинами, у которых кроме числа есть еще и направление – ускорение, сила.
Немного отвлечемся, и обсудим, что такое вектор.
Вектор – это математический объект, у которого есть величина и направление.
В геометрии вектор – это направленный отрезок. Он имеет величину, равную длине отрезка, и направление.
Например, в случае двигающегося автомобиля принято показывать его направление движения стрелкой, а длина этой стрелки обычно указывает на величину скорости по модулю. Модуль, напомню, все отрицательные величины превращает в положительные. Чем больше длина стрелки, тем больше скорость машины. (См.Рис.3.)
В случае 1 стрелка у красной машины указывает нам на то, что автомобиль двигается вправо. Стрелка подписана сверху (vec{|V_1|}=90(км/ч)). Эта запись означает, что величина скорости красной машины по модулю равна (90(км/ч)).
Если я напишу вектор скорости красной машины без модуля, то он будет выглядеть вот так:
$$ vec{V_1}=+90(км/ч);$$
Знак плюс указывает на то, что скорость машины сонаправлена с выбранной нами осью (х).
В случае 2 синяя машина двигается влево. Ее вектор скорости запишется так:
$$vec{V_2}=-45(км/ч);$$
Знак минус указывает на то, что машина едет в противоположную сторону оси (х).
Как видите, по одной только записи вектора можно сразу сказать, куда едет машина и с какой скоростью – это очень удобно. Знак указывает на направление, а число – на величину.
Обратите внимание, что у красной машины вектор скорости длиннее, чем у синей, это означает, что красная едет быстрее. Не глядя на числа, мы можем с уверенностью сказать это, посмотрев на рисунок. Так принято обозначать. Это тоже удобно.
Равномерное движение
Любое движение с постоянной скоростью называется равномерным движением. Все, что мы рассматривали выше – это примеры равномерного движения.
Теперь мы готовы составить первые уравнения, описывающие равномерное движение. В кинематике нас будет интересовать уравнение, которое описывает положение тела в пространстве в зависимости от времени (изменение координаты тела со временем). Оно выглядит так:
$$ x(t)=x_0+V*t;$$
(x_0) – это начальная координата тела, где оно находилось в момент времени (t=0). Например, на рис.2. начальная координата автомобиля (x_0=3(м)).
(V) – это скорость, с которой двигается тело.
(t) – это время, которое прошло с момента начала движения.
(x(t)=x_{конечная}) – это конечная координата, то есть координата, где окажется тело через время (t). Я написал (x(t)), чтобы показать, что координата тела зависит от времени, ведь в разные моменты времени двигающееся тело находится в разных точках.
Разберем на примере, как работает это уравнение.
Пример 1
Автомобиль начал движение из координаты (x_0=-3(м)) со скоростью (V=5(м/с)) вправо. Где будет автомобиль через 3 секунды? Через какое время автомобиль окажется в точке с координатой (x=12(м))?
Решение: Первым делом всегда рисуем рисунок, он поможет правильно расставить знаки в уравнениях и лучше представить задачу. Чтобы ответить на поставленные вопросы, воспользуемся уравнением для координаты при равномерном движении (x(t)=x_0+V*t.)
Подставим известные величины:
$$x(t)=-3+5*t;$$
Обратите внимание, что скорость входит в уравнение со знаком (+), так как автомобиль едет по условию вправо, а это сонаправленно с осью (х). Если бы он ехал влево, то уравнение выглядело бы так: $$x(t)=-3-5t.$$
Получили уравнение, которое полностью задает движение автомобиля.
Действительно, если в это уравнение подставить некоторое время вместо (t), то можно узнать координату, где находится автомобиль в различные моменты времени.
Например, если (t=0), момент начала движения:
$$x(t=0)=-3+5*0=-3(м);$$
Логично, что в начале автомобиль находился в координате (x_0=-3). Чтобы узнать, где он будет через секунду, подставим (t=1(c)):
$$ x(t=1)=-3+5*1=-3+5=2(м);$$
Отрицательное время подставлять нет смысла, так как время не может быть отрицательным. А координата и скорость могут.
Теперь вспоминаем про задачу. Нам нужно узнать, где будет машина через 3 секунды. Просто подставляем в уравнение (t=3(с)):
$$ x(t=3)=-3+5*3=-3+15=12(м);$$
А как понять, через сколько по времени машина окажется в координате (x(t)=12(м))? Подставим:
$$12=-3+5*t;$$
Осталось решить простое линейное уравнение:
$$t=3(c).$$
Ответ: ( x(t=3)=12(м);) и (t=3(c)).
Равноускоренное движение
Если скорость не меняется, то все понятно. А что делать если скорость непостоянна?
В школе рассматривается случай, когда скорость у тела изменяется (увеличивается или уменьшается) равномерно, то есть за каждую следующую секунду скорость увеличивается/уменьшается на одну и ту же величину. Такое движение называют равноускоренным или равнозамедленным соответственно.
Пример такого движения. Представьте, что лыжник скатывается с горки из состояния покоя, при этом его скорость постоянно увеличивается, например, на 2 м/с ежесекундно. То есть:
$$V(t=0)=0(м/с);$$
$$V(t=1)=V(t=0)+2=0+2=2(м/с);$$
$$V(t=2)=V(t=1)+2=2+2=4(м/с);$$
$$V(t=3)=V(t=2)+2=4+2=6(м/с);$$
$$V(t=4)=V(t=3)+2=6+2=8(м/с);$$
Величина, на которую ежесекундно увеличивается/уменьшается скорость, называется ускорением и обозначается буквой (a).
Ускорение измеряется в (frac{м}{с^2}).
Разумеется, в жизни бывают случаи, когда скорость изменяется неравномерно. Но в школьном курсе такие задачи крайне редкие, и мы их рассматривать не будем.
Как выглядит уравнение, описывающие равноускоренное движение?
$$x(t)=x_0+V_0*t+frac{a*t^2}{2};$$
По сравнению с равномерным движением, у нас добавилось еще одно слагаемое (frac{a*t^2}{2}), которое отвечает за ускоренность/замедленность движения.
Так как скорость теперь переменная величина, для нее тоже можно записать уравнение:
$$V(t)=V_0+at;$$
- (x_0) – начальная координата тела;
- (V_0) – начальная скорость тела; скорость, с которой тело начало движение;
- (x(t)) – конечная координата;
- (V(t)) – конечная скорость;
- (a) – ускорение;
- (t) – время.
Уравнения для координаты и для скорости при равноускоренном движении являются основными уравнениями всей школьной кинематики. Если в них хорошо разобраться, то больше никаких формул учить не нужно. Все выводится из них. Я рекомендую пользоваться только этими двумя уравнениями и не забивать себе голову ничем посторонним.
Внимание! Вообще говоря, ускорение — это векторная величина, так же, как и скорость. Мы это обсуждали в начале темы. И помним, что если вектор сонаправлен с выбранным нами направлением оси координат, то ускорение положительно, а если нет, то отрицательно.
Если же вектора скорости и ускорения направлены в одну сторону, то тело ускоряется. А если в разные, то тормозит.
Посмотрите на рисунки:
В случае а) скорость сонаправлена с осью х, значит она будет положительна. Ускорение тоже сонаправлено с осью х, значит оно положительно. А раз вектора скорости и ускорения направлены в одну сторону, то это значит, что тело ускоряется.
Случай б): скорость положительна, ускорение отрицательно. Раз вектор скорости и вектор ускорения направлены в разные стороны, значит тело замедляется.
Случай в): скорость и ускорение отрицательны, но сонаправлены – тело ускоряется.
Случай г): скорость отрицательна, ускорение положительно – тело замедляется.
Со знаками разобрались, теперь давайте разберем пример.
Пример 2
Лыжник скатывается с горки с нулевой начальной скоростью ((V_0=0(м/с))). Через 5 секунд после начала движения его скорость была (V(t=5(c))=15(м/с)). Определите с каким ускорением движется лыжник и какое расстояние он проедет за 10 секунд?
Решение:
Рисуем рисунок, чтобы представить, что происходит, и правильно расставить знаки. Ось х выбираем, как угодно. Я направил вниз.
Как мы уже обсуждали выше, у нас есть всего два уравнения – для координаты и для скорости, которые полностью описывают любое движение:
$$x(t)=x_0+V_0*t+frac{a*t^2}{2};$$
$$V(t)=V_0+at;$$
Так как нам даны начальная и конечная скорости, то разумно воспользоваться уравнением для скорости. Не забываем про знаки скорости и ускорения – оба вектора сонаправлены с выбранной мною осью х, а значит, и скорость, и ускорение будут в уравнениях положительны.
$$V(t)=V_0+at;$$
$$15=0+a*5;$$
$$a=frac{15}{5}=3frac{м}{с^2};$$
Зная ускорение, с которым движется лыжник, мы можем найти, где будет лыжник через 10 секунд, используя уравнение для координаты:
$$x(t=10)=x_0+V_0*t+frac{a*t^2}{2}=0+0*10+frac{3*10^2}{2}=150(м);$$
Таким образом, мы получили, что лыжник за 10 секунд успеет проехать (150) метров, если будет двигаться с постоянным ускорением (a=3(frac{м}{с^2})).
Работа с графиками в кинематике
В ЕГЭ по физике кинематика часто встречается в самом первом задании и, как правило, там задача с графиками. Графики помогают нам визуально описывать поведение одной некоторой величины в зависимости от другой. В школе вы должны были часто строить графики зависимостей (y) от (x). В кинематике же обычно строят графики зависимости координаты или скорости от времени. Давайте построим пару таких графиков и обсудим, как их читать.
Главное, нужно понять, что перед вами не траектория и не картинка, на которой изображено, как движется тело. Это зависимость одной физической величины от другой. На наших рисунках изображены графики зависимостей координаты и скорости от времени некоторого объекта (пусть это будет велосипедист) при различных видах движения. Например, на графике ((в)) НЕ показано движение некоторого объекта в гору, а просто координата по мере движения увеличивается.
- На графике ((а)) показана зависимость координаты велосипедиста от времени. В моменты времени (t_1) и (t_2) велосипедист находится в одной и той же координате, а значит, он стоит на месте. То есть здесь велосипедист находится в покое.
- На графике ((б)) зависимость скорости от времени. Визуально он очень похож на график ((а)), но смысл совершенно другой. Так как тут показана скорость, мы видим, что в моменты времени (t_1) и (t_2) у велосипедиста была одна и та же скорость (V_0). А раз в различные моменты времени скорость одинаковая, то это равномерное движение или движение с постоянной скоростью. Более того, еще можно сделать вывод, что велосипедист движется вправо (туда, куда направлена ось (х)), потому что скорость положительна.
- В ((в)) линейная зависимость координаты тела от времени (то есть по прямой). Замечаем, что координата с течением времени увеличивается, а это значит, что объект движется вправо. Если бы координата уменьшалась, то движение было бы влево (в противоположную сторону оси (х)). Отметим на графике несколько точек через одинаковый интервал времени. В момент времени (t_1) велосипедист был в координате (x_1), а в момент (t_2) в (x_2). За время (Delta t=t_2-t_1) он прошел расстояние (Delta x=x_2-x_1). И за каждый следующий промежуток времени (Delta t) он будет проходит одинаковое расстояние (Delta x). Это означает, что он двигается с одной и той же скоростью – равномерное движение.
- График под пунктом ((г)) показывает нам линейный рост скорости от времени. Если посмотреть, какая скорость будет у велосипедиста через одинаковые промежутки времени, то мы увидим, что она все время растет на одинаковую величину (Delta V). Если скорость растет, то значит движение ускоренное, а если растет еще и линейно, то равноускоренное. Скорость здесь положительна, значит велосипедист едет вправо (туда, куда направлена ось (х)).
- График ((д)) – это зависимость координаты от времени. Видно, что каждый следующий промежуток времени координата успевает измениться на бОльшую величину – за время (t_4-t_3) он проходит бОльшее расстояние, чем за (t_2-t_1). Значит велосипедист ускоряется. Так как координата по ходу движения уменьшается, значит он двигается влево (противоположную сторону оси (х)).
- И на последнем графике ((е)) показана зависимость скорости от времени. Видим, что скорость с течением времени уменьшается, и каждый следующий промежуток времени скорость меняется быстрее, чем на предыдущем. Так как скорость положительна, велосипедист едет вправо (туда же, куда направлена ось х). Так как скорость уменьшается неравномерно, значит на рисунке показано замедленное движение с переменным ускорением.
Движение в поле тяжести Земли
Теперь рассмотрим движение объектов в поле тяжести нашей планеты Земли. Любое тело, свободно падающее (отпущенное с некоторой высоты без начальной скорости) на Земле, будет двигаться с ускорением свободного падения (g=9.8(м/с^2)). Важно помнить, что (g) всегда направлено к центру Земли.
Внимательно посмотрите на рисунок 8: на нем изображено движение камня, брошенного вертикально вверх с некоторой начальной скоростью (V_0). Сначала он будет двигаться равнозамедленно, пока не достигнет наивысшей точки подъема (H), там остановится (скорость (V=0)), и начнет падать обратно, постепенно набирая скорость, пока не упадет обратно к вам в руку со скоростью (V_к). Для того, чтобы лучше разобраться, представьте, что вы подбросили вверх камень – он будет двигаться именно так, как мы обсудили. Таким образом, задачи на движение в поле тяжести Земли ничем не отличаются от задач равноускоренного / равнозамедленного движения по дороге, только на этот раз нам всегда известно ускорение — (g=9.8 (м/с^2)).
Давайте составим уравнения, описывающие это движение. Как всегда, их будет два – для скорости и для координаты:
$$y(t)=y_0+V_0*t-frac{g*t^2}{2};$$
$$V(t)=V_0-gt;$$
Что изменилось?
- Во-первых, координата теперь не (x), а (y) – тело двигается вдоль вертикальной оси, а ее принято обозначать за (Y).
- Вместо ускорения (a) мы теперь пишем (g) – ускорение свободного падения, оно нам известно.
Разбираемся со знаками: начальная скорость (V_0) направлена вверх (сонаправленно с осью (Y)). Ускорение во время всего движения направленно вниз к центру Земли (в противоположную сторону (Y)). Получаем, что в системе координат, выбранной на рисунке, начальная скорость будет с плюсом, а ускорение с минусом. Систему координат вы можете выбрать и другую, но тогда знаки будут меняться в соответствии с правилами расстановки знаков.
Обратите внимание!Не нужно писать отдельно уравнения для движения вверх и вниз. Уравнения сами учитывают, что тело после подъема полетит вниз.
Решим несколько задач и обсудим еще пару важных нюансов.
Пример 3
Пусть камень брошен вертикально вверх с начальной скоростью (V_0=10(м/с)). Найдите максимальную высоту подъема и время полета.
Решение
Для решения воспользуемся старым рисунком (рис.8).
Любая задача начинается с написания уравнений в общем виде:
$$y(t)=y_0+V_0*t-frac{g*t^2}{2};$$
$$V(t)=V_0-gt;$$
Выберем за начальное положение тела внизу, на Земле. А за конечное – наивысшую точку. Координата камня в наивысшей точке подъема будет — (y(t)=H), а скорость будет равна (V(t)=0 ) (смотрите на рисунок 8).
Важно! Скорость в наивысшей точке подъема будет равна 0 (камень останавливается), мы часто будем это использовать при решении подобных задач.
Начальная координата (y_0=0).
Начальная скорость (V_0=10(м/c)) из условия.
Получим уравнения:
$$H=10*t-frac{9.8*t^2}{2};$$
$$0=10-9.8*t;$$
Из уравнения для скорости можно найти время полета от Земли до наивысшей точки:
$$t=10/9.8=1.02 /,(с)$$
Подставим в первое уравнение:
$$H=10*1.02-frac{9.8*1.02^2}{2}=5.1 (м);$$
Обращаю ваше внимание, что (t) – время полета от Земли до наивысшей точки. А по условию задачи нам нужно найти время всего полета. Для этого нужно время подъема умножить на два.
Важно! Время подъема всегда равно времени падения.
$$T=2*t=1.02*2=2.04 c.$$
Ответ: (T=2.04 /,(с).)
Пример 4
Рассмотрим падение камня с некоторой высоты (H) вертикально вниз с начальной скоростью (V_0). Как тогда будут выглядеть уравнения, описывающие движение камня? (см. Рис.9.)
За конечное положение выберем Землю (y(t)=0), за начальное — высоту (y_0=H).
$$0=H-V_0*t-frac{g*t^2}{2};$$
$$-V_к=-V_0-gt;$$
Знаки расставлены с учетом направления осей координат.
Многие часто полагают, что при броске камня вниз, его конечная скорость у земли будет равна 0, ведь камень останавливается. Но это не так. К сожалению, уравнения кинематики не учитывают воздействие земли на камень, поэтому, говоря «конечная скорость», мы подразумеваем скорость за мгновение до удара о землю, и она, очевидно, не будет равна нулю.
Основные моменты
- В поле тяжести Земли вертикально брошенное тело всегда движется с ускорением свободного падения (g=9.8(м/с^2)).
- Если тело бросили с земли и оно упало обратно на землю, то время падения равно времени подъема.
- Скорость в верхней точке подъема всегда равно нулю.
Рассмотрим, как выглядят графики зависимостей координаты и скорости от времени при бросании камня.
Бросок тела вертикально вверх
Чтобы хорошо разобраться, рекомендую представить полет камня.
Скорость.При движении вверх скорость камня линейно уменьшается, он тормозит с ускорением (g), пока не остановится в верхней точке. После этого камень сразу начинает падать вниз, скорость увеличивается также с ускорением (g). Если же его бросили с земли, и он упал обратно на землю, то начальная скорость броска будет равна конечной скорости за мгновение до удара о землю. (Рис. 10 (б))
Координата. На рисунке 10 (а) изображено, как меняется координата (y(t)) в зависимости от времени полета. Обратите внимание на форму графика – это парабола. Не попадайтесь в визуальную ловушку, перед вами НЕ линия вдоль которой движется камень, в просто зависимость координаты от времени. Видно, что в начале полета тело успевает пройти за единицу времени большее расстояние, чем ближе к середине полета – координата растет сначала быстро, а потом все медленнее и медленнее, и останавливается в наивысшей точке подъема. Это связано с тем, что скорость в начале полета больше. Затем тело начинает падать, постепенно набирая скорость, и координата начинает изменяться все быстрее и быстрее, пока тело не упадет обратно на землю. (Рис. 10 (а))
Аналогичные рассуждения для броска камня вниз с нулевой начальной скоростью. (См. Рис.11)
Рис.10. Бросок камня вертикально вверх
Рис.11. Бросок тела вертикально вниз с нулевой начальной скоростью
Движение тела под углом к горизонту
До этого мы рассматривали одномерные задачи, где движение происходило вдоль одной прямой. В школьном курсе физики подавляющее большинство задач двумерны.
Рассмотрим классическую двумерную задачу кинематики – бросок камня под углом к горизонту в поле тяжести Земли. Представьте, что вы играете в игру, кто дальше кинет камень. Траектория камня будет похожа на параболу, зеленая линия. (См. Рис. 12) Именно такое движение мы и постараемся описать при помощи математики. Для этого нам понадобится двумерная система координат (XoY). Ось (X) будет отвечать за дальность полета, ось (Y) – за высоту. Точка (O) – точка начала движения. (V_0) – начальная скорость, скорость, которую мы придали камню в момент броска. Точка (А) – точка наивысшего подъема.
Рис.12. Движение под углом к горизонту
Для того, чтобы описать такое сложное двумерное движение, разобьем его на два – отдельно горизонтальное, и отдельно вертикальное движения. Мы можем представить, что наш камень в некоторый момент времени летит с вертикальной скоростью (V_y) и ускорением (a_y) вдоль оси (Y), и с горизонтальными скоростью (V_x) и ускорением (a_x) вдоль оси (X). Вместе эти два движения, если их наложить друг на друга, дают сложное двумерное движение по зеленой параболе с скоростью (V) и ускорением (a).
Скорость тела при двумерном движении в любой момент времени направлена по касательной к траектории. На рис.12. она показана красными стрелками в точках (О, А) и (В).
Рассуждая таким образом, мы можем записать уравнения для координаты и скорости по вертикали и потом по горизонтали – всего 4 уравнения, каждое из которых отвечает за свою ось.
$$y(t)=y_0+V_{0y}*t+frac{a_{y}*t^2}{2};$$
$$V_{y}(t)=V_{0y}+a_{y}*t;$$
$$x(t)=x_0+V_{0x}*t+frac{a_{x}*t^2}{2};$$
$$V_{x}(t)=V_{0x}+a_{x}*t;$$
Возникает справедливый вопрос, откуда нам взять все горизонтальные и вертикальные скорости. Есть начальная скорость (V_0), одновременно направленная по обеим осям. Нам нужно как-то рассмотреть эту скорость, как совокупность двух отдельных скоростей – горизонтальной и вертикальной. Вот для этого нам понадобится некоторый математический прием – проекции.
Проекция вектора
Пусть у нас есть некоторый вектор (vec{a}). Напоминаю, что вектор – это направленный отрезок. У него есть начало – т.А, и конец – т.В. (см.Рис.13). Опустим перпендикуляры из точек А и В на ось (Х). Получим соответственно точки (A_x) и (B_x), который называются проекциями точек (A) и (В) на ось (Х). Получившийся отрезок ({A}_{x} {B}_{x}) будет называться проекцией вектора (vec{a}) на ось (Х). Для краткости записи обозначим ({A}_{x} {B}_{x}=a_x) Аналогичным образом получим проекцию (vec{a}) на ось (Y): ({A}_{y} {B}_{y}=a_y).
Посчитаем чему равны (a_x) и (a_y), если нам известен угол и длина вектора (vec{a}). Достроим наш вектор до прямоугольного треугольника с гипотенузой (vec{a}) и катетами (a_x) и (a_y) (На рис.13. показаны зеленым).
Напоминаю, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, а косинус – прилежащего катета к гипотенузе:
$$ sin{alpha}=frac{a_y}{a};$$
$$cos{alpha}=frac{a_x}{a};$$
Из этих формул можно выразить (a_x) и (a_y):
$$a_x=a*sin{alpha};$$
$$a_y=a*cos{alpha}.$$
Таким образом, зная длину вектора и угол, мы можем легко найти его проекции. Запомните это.
Вернемся к нашей задаче. Мы остановились на том, что нужно найти горизонтальную и вертикальную составляющие начальной скорости и ускорения. Оказывается, проекции начальной скорости (V_0) на оси (X) и (Y) и будут искомыми начальными скоростями по горизонтали и вертикали. (См. Рис. 12). Оранжевым показаны проекции (V_{0x})- начальная горизонтальная скорость, и (V_{0y})-вертикальная. Заметим, что (BB_x=V_{0y}) и (AB_x=V_{0x}). (См. Рис.14.). Из треугольника (ABB_x) получаем:
Рис.14. Проекция скорости на оси х и y
$$sin{alpha}=frac{BB_x}{AB}=frac{V_{0y}}{V_0};$$
$$cos{alpha}=frac{AB_x}{AB}=frac{V_{0x}}{V_0}.$$
Отсюда
$$V_{0y}=V_0*cos{alpha};$$
$$V_{0x}=V_0*sin{alpha}.$$
Зная угол к горизонту (alpha), под которым бросили тело, и его начальную скорость, мы можем по формулам выше найти начальные скорости для горизонтального и вертикального движений.
Разберемся теперь с каким ускорением движется тело по вертикали и горизонтали. Если вы бросаете камень на Земле, то у него будет вертикальное постоянное ускорение, направленное к центру Земли – ускорение свободного падения (g=9,8(м/с^2)). (См.Рис.12).
По горизонтали ускорение, оказывается, будет равно нулю. Другими словами, по горизонтали камень будет лететь равномерно, с постоянной скоростью. Это связано с тем, что в горизонтальном направлении на тело во время полета не действует никаких сил, то есть ничто не может изменить его скорость. А по вертикали действует сила притяжения Земли, которая вызывает ускорение свободного падения.
Можно просто запомнить, что по вертикали ускорение всегда (g), а по горизонтали ускорение 0.
Используем все наши рассуждения для записи системы уравнений, описывающих движение под углом к горизонту:
$$y(t)=y_0+V_{0y}*t+frac{a_{y}*t^2}{2};$$
$$V_{y}(t)=V_{0y}+a_{y}*t;$$
$$x(t)=x_0+V_{0x}*t+frac{a_{x}*t^2}{2};$$
$$V_{x}(t)=V_{0x}+a_{x}*t;$$
Подставим (V_{0x}=V_0*sin{alpha},, V_{0y}=V_0*cos{alpha},, a_x=0,,a_y=g):
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Знания и понимания этих четырех уравнений достаточно, чтобы решить любую школьную задачу по кинематике. Часто в школах дают большое количество формул, связывающих расстояние, скорость и ускорение и т.п. Если вы разобрались, как были получены уравнения выше, то в этих формулах нет необходимости. Они легко выводятся.
Основные моменты движения тела, брошенного под углом к горизонту:
- Сложное двумерное движение разбиваем на два: горизонтальное и вертикальное.
- Ускорение по вертикали равно ускорению свободного падения и всегда направлено вниз, к центру Земли. Ускорение по горизонтали в отсутствии сопротивления воздуха равно 0. По горизонтали движение равномерное.
- Скорость полета тела всегда направлена по касательной к траектории полета. Скорость по горизонтали и вертикали можно найти соответственно из формул:
$$V_x=V*cos{alpha};$$
$$V_y=V*sin{alpha};$$ - Дальностью полета называют расстояние по горизонтали между точкой броска и точкой падения камня на землю. На рис.12. дальность показана буквой (S).
- Время подъема равно времени падения. При условии, что тело бросили с Земли и оно упало обратно на Землю.
- Скорость по вертикали в наивысшей точке подъема равна 0. Этот факт часто используют для нахождения времени подъема до наивысшей точки из уравнения для скорости по оси (y):
$$0=V_{0y}-gt.$$
Разберем несколько задач на движение под углом к горизонту.
Пример 5
Камень бросили под углом (alpha=30^о) к горизонту с начальной скоростью (V_0=20(м/с)). Найти дальность его полета. И максимальную высоту подъема.
Бросок камня под углом к горизонту
Решение
Первым делом выпишем все уравнения в общем виде:
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Начальная скорость направлена вверх и вправо, поэтому в уравнениях она будет со знаком плюс. Ускорение свободного падения направлено вниз – ставим минус.
Выбираем начальное и конечное положение тела, для которого будем записывать уравнение. Логично, что начальная точка – это момент броска с координатами (0;0), а за конечную выберем т.А ((S/2;H)) – наивысшую точку подъема, так как мы знаем, что скорость там по оси (y): (V_y=0).
Подставим координаты и известные величины в систему уравнений:
$$H=20*sin{30}*t-frac{9.8*t^2}{2};$$
$$0= 20*sin{30}-9.8*t;$$
$$S= 20*cos{30}*t;$$
$$V_{x}= 20*cos{30}.$$
Из уравнения для скорости по (y) (2-е уравнение) можно найти (t) – время подъема тела до наивысшей точки.
$$t=frac{20*sin{30}}{9.8}=1.02 (c);$$
Чтобы найти максимальную высоту подъема, подставим найденное время в первое уравнение для координаты (y). Камень будет в наивысшей точке через половину времени полета, потому что время подъема равно времени падения:
$$H=20*sin{30}*1.02-frac{9.8*1.02^2}{2}=5.1(м);$$
Полное время полета:
$$T=2*t=2.04 (c);$$
Найдем дальность, используя уравнения для координаты (x):
$$S= 20*cos{30}*2.04=35.3(м);$$
Мы решили задачу. Рассчитали высоту (H) и дальность полета камня (S), если бросить его под углом в (30^0) и с начальной скоростью (V_0=20(м/с)). Весь полет займет чуть больше 2-х секунд.
Ответ:(S=35.3(м)) и (H=5.1(м)) и (T=2.04(c)).
Пример 6
Камень бросили с балкона с высоты (y_0=20(м)), придав ему начальную скорость (V_0=10(м/с)) и под углом к горизонту (60^0).Найти дальность и максимальную высоту полета.
Бросок камня под углом к горизонту с некоторой высоты
Решение:
Запишем уравнения в общем виде:
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Подставим все данные в уравнения для координат, согласно условию задачи. За начальную точку выберем точку броска (x_0=0, . y_0=H_0), а за конечную точку падения (x(t)=S, . y(t)=0):
$$0=H_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$S= V_0*cos{alpha}*t;$$
С учетом данных в условии задачи
$$0=20+10*sin{60^0}*t-frac{g*t^2}{2};$$
$$S= 10*cos{60^o}*t;$$
Выразим время всего полета
$$20+5sqrt{3}*t-4.9*t^2=0;$$
Решаем через дискриминант квадратное уравнение и находим время всего полета
$$t=3.04(с);$$
Чтобы найти дальность полета, подставим найденное время в уравнение для координаты (х)
$$S= V_0*cos{alpha}*t;$$
$$S= 10*cos{60^0}*3.04=15.2(м);$$
Обращаю внимание, что в данной задаче время подъема не равно времени падения, так как задача несимметричная – камень бросают с балкона, а падает он на землю.
Для нахождения максимальной высоты подъема воспользуемся тем, что скорость по (Y) в верхней точке траектории равна (0), и найдем время полета до этой точки:
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$0= 10*sin{60^0}-g*t;$$
$$t=0.88(c);$$
Подставим найденное время в уравнение для координаты (у):
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$H=20+10*sin{60^0}*0.88-frac{9.8*0.88^2}{2}=28.65-3.79=24.86(м).$$
Ответ: (S=15.2(м)) и (H=24.86(м)).
Пример 7
Тело бросили ГОРИЗОНТАЛЬНО с балкона высотой 20 метров ((H_0=20м)) с начальной скоростью (V_0=10м/с). Найти под каким углом к горизонту будет направлена скорость тела через (t=0.5 с), время всего полета и дальность.
Рис.15. Бросок тела с некоторой высоты горизонтально
Как обычно, начинаем решение задачи с написания всех уравнений в общем виде:
$$y(t)=y_0+V_{0Y}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_{0Y}-g*t;$$
$$x(t)=x_0+ V_{0X}*t;$$
$$V_{x}(t)= V_{0X}.$$
Найдем время всего полета и дальность. Начальная точка – это точка броска с координатами ((0;H_0)), конечная точка – падение на Землю ((L;0)).
Обратите внимание, что начальная скорость тела горизонтальна, а значит у нас нет вертикальной составляющей начальной скорости – мы не сообщаем телу начальную скорость по (Y). Поэтому (V_{0y}=0), а (V_{0x}=V_0).
Уравнение по (Y) принимает вид:
$$0=H_0-frac{g*t^2}{2};$$
$$0=20-frac{9.8*t^2}{2};$$
Находим время всего полета
$$t=sqrt{frac{2*20}{9.8}}=2,02(c);$$
Чтобы найти дальность, подставим найденное время в уравнение для координаты (х)
$$L=V_0*t=10*2.02=20.2(м);$$
И осталось ответить на последний вопрос – под каким углом к горизонту будет направлена скорость через (t=0,5(c)). Предположим, что тело в этот момент будет находиться в точке (А) (См.Рис.15). Скорость тела в любой момент времени направлена по касательной к траектории — (V_A).
Для решения этой задачи нам понадобится найти проекции (V_A) на оси (X) и (Y), на рисунке они показаны оранжевым цветом — (V_{AX};. V_{AY}).
Так как движение по горизонтали равномерное, то скорость по (X) в любой момент времени будет постоянна и равна начальной скорости (V_0).
Для нахождения (V_{AY}) запишем уравнение для скорости по (Y)
$$V_{y}(t)= V_{0Y}-g*t;$$
$$V_{0Y}=0;$$
$$V_{y}(t=0.5c)=-g*t;$$
$$V_{y}(t=0.5c)=-9.8*0.5=-4.9м/с;$$
Скорость получилась отрицательная, потому что она направлена вниз – в противоположную сторону оси (Y).
Рис.16. Проекции скорости в произвольной точки траектории
Зная проекции скорости (V_{AX}) и (V_{AY}) мы можем найти угол, под которым направлена скорость. Посмотрите на рис.16. Так как (ABCD) прямоугольник, то (AB=CD=V_{AX}). Тогда из треугольника (ADC) можно найти тангенс (alpha)
$$tg{alpha}=frac{V_{AY}}{V_{AX}}=frac{4.9}{10}=0.5;$$
$$alpha=27^0.$$
Ответ: (t=2.02(c);, L=20.2(м);, alpha=27^0.)

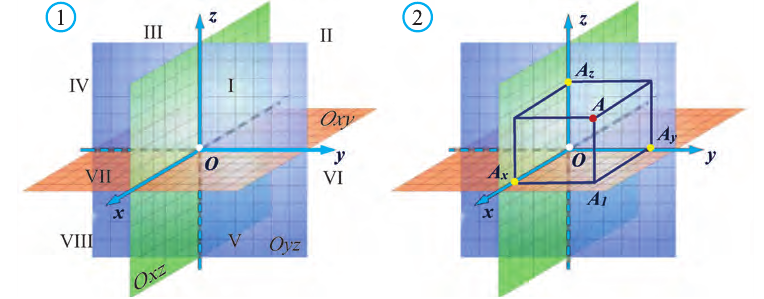
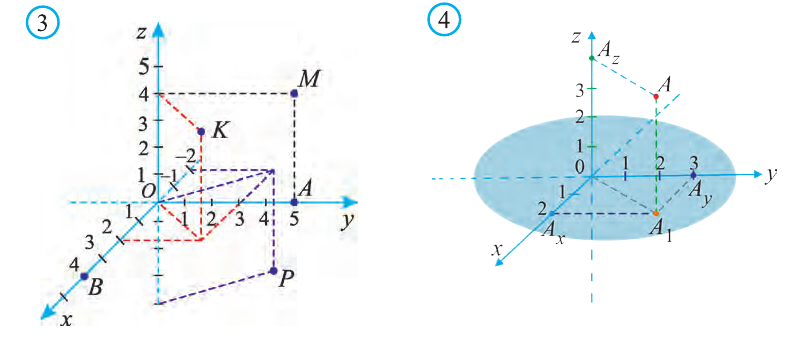

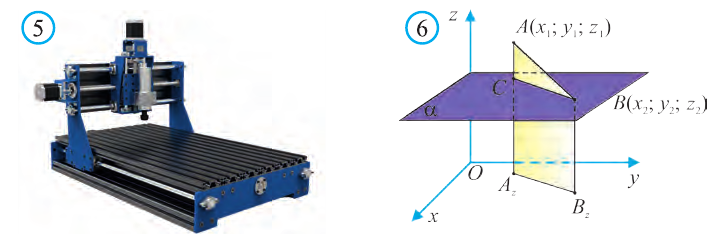
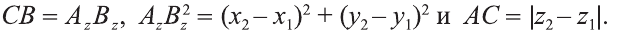
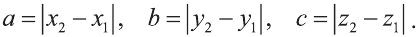
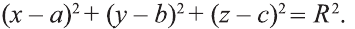
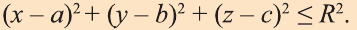
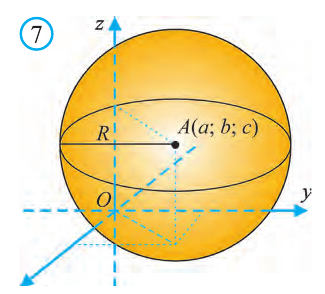
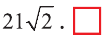
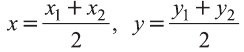
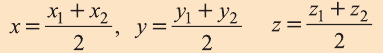
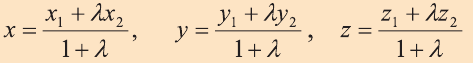
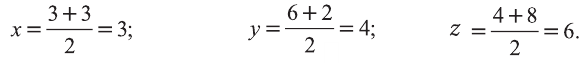
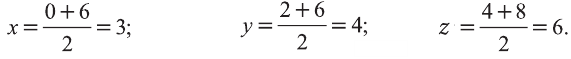

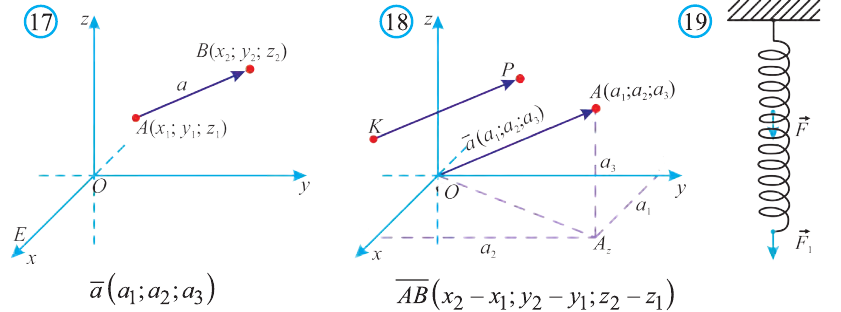
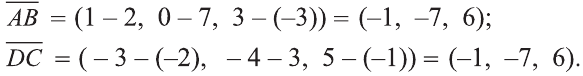
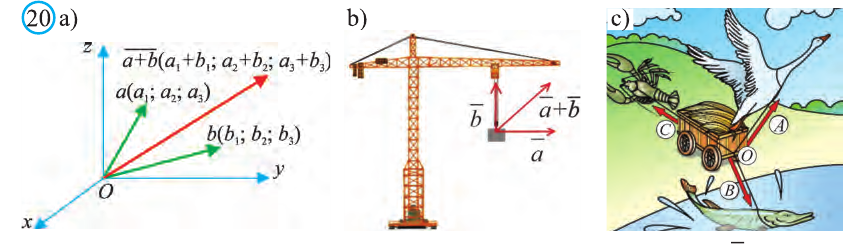
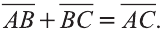
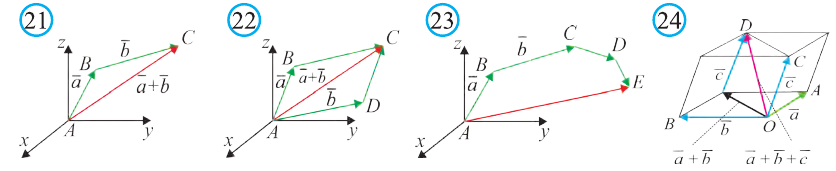
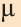
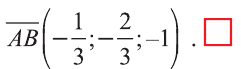
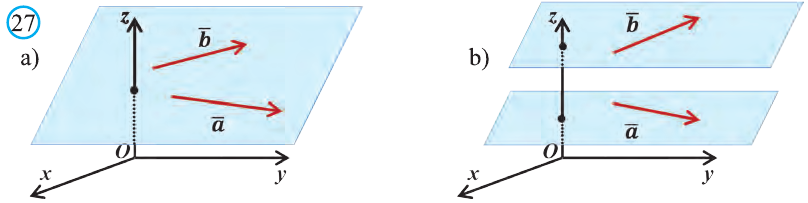
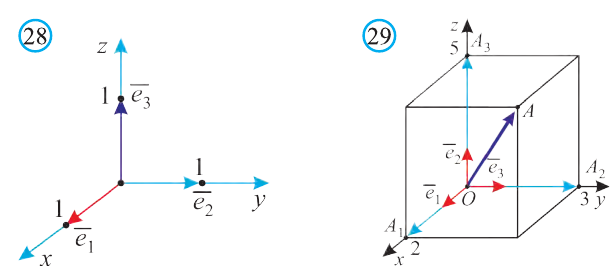
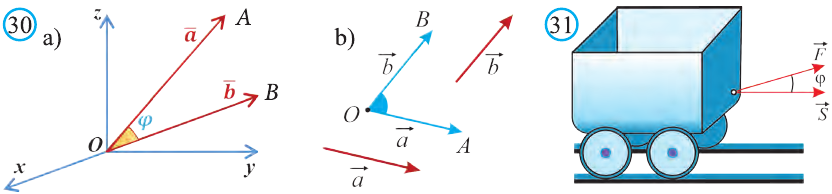
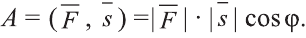
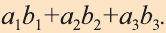
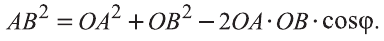
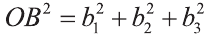
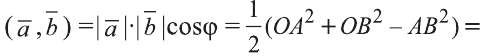
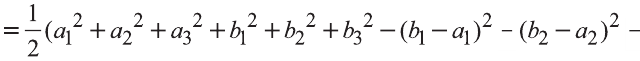

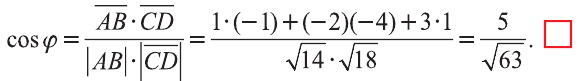
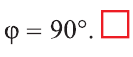
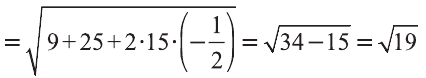
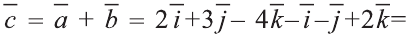
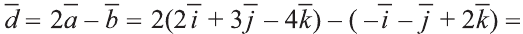
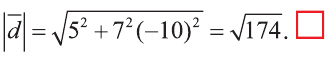
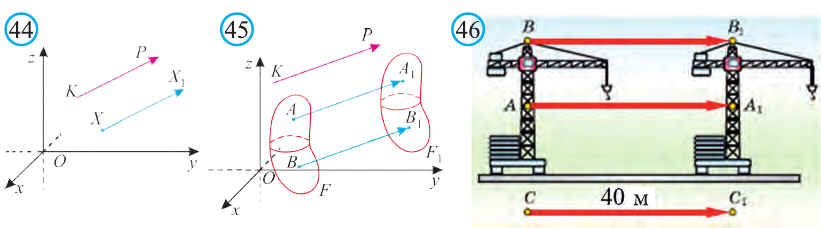

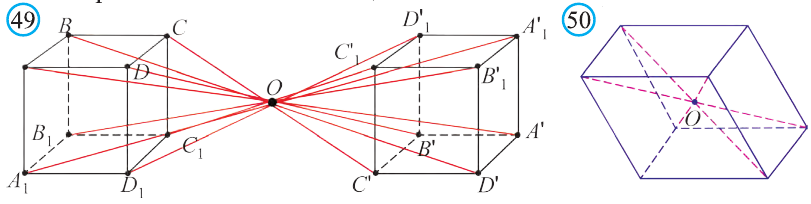
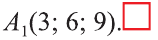
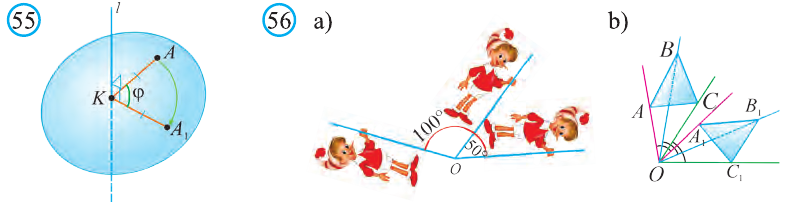










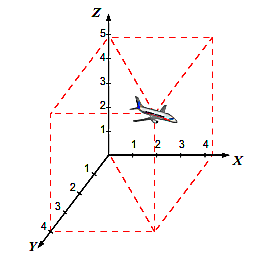
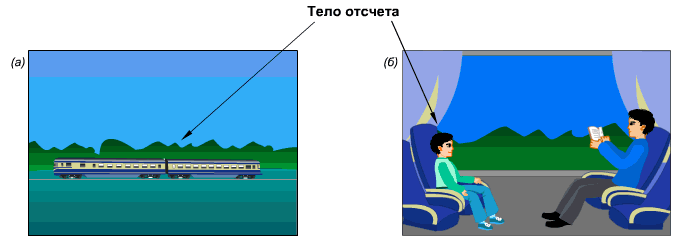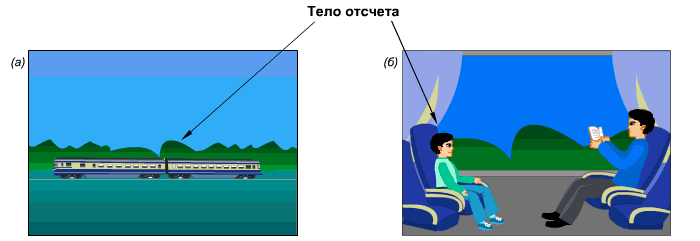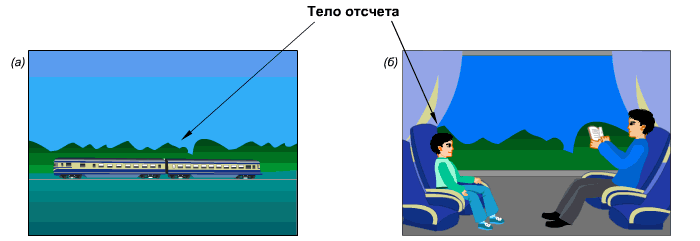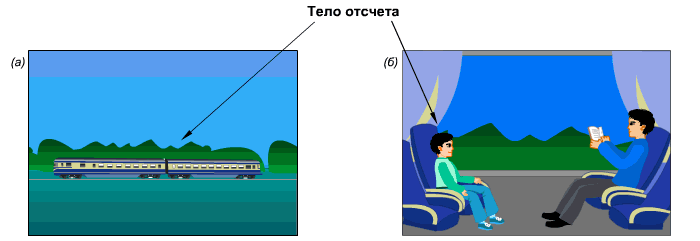










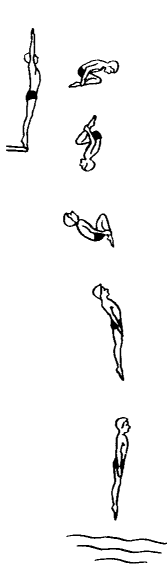



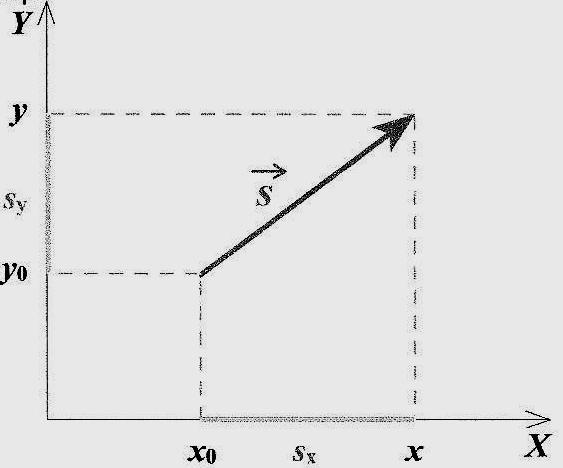
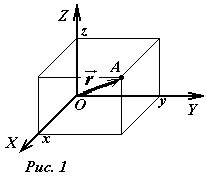
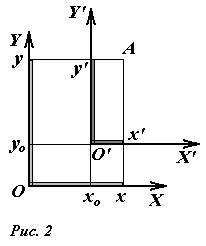
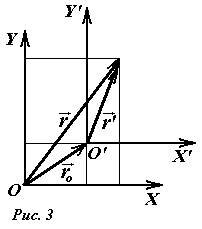
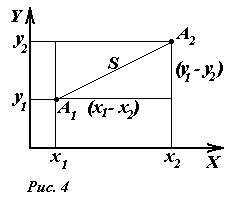
 и
и  называется число c , равное произведению модулей векторов на косинус угла α между ними:
называется число c , равное произведению модулей векторов на косинус угла α между ними:  .
.
















