Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?
В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.
Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.
Примеры.
1)

A(-3;11), B(12;-4), C(1;-7)
Найти: D.
Решение:

По формуле координат середины отрезка
То есть O(-1;2).
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:
Ответ: D (-14; 8).
2)
Дано: ABCD — параллелограмм,
B(7;4), C(-5;10), D(-1;-2)
Найти: A.
Решение:
1) Ищем координаты точки O — середины отрезка BD:
Итак, O (3;1).
2) Точка O также является серединой AC:
Ответ: A (11;-8).
Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
Договорились координатную плоскость с осью
Координаты точки на плоскости 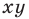
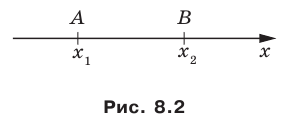
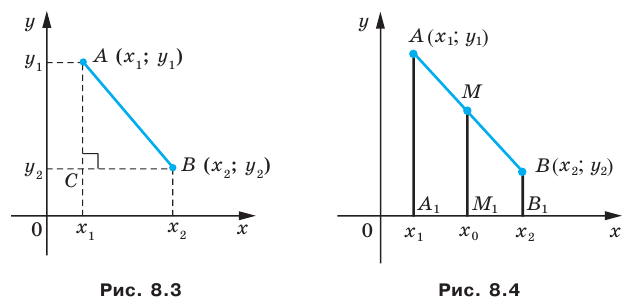
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 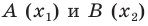
Научимся находить расстояние между точками 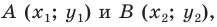
Рассмотрим случай, когда отрезок 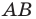
Через точки 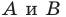
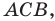
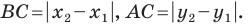
Тогда формулу расстояния между точками 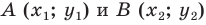
Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 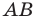
Пусть 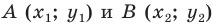
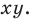
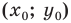
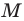
Рассмотрим случай, когда отрезок 
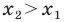
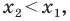
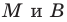
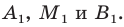
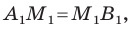
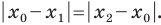
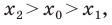
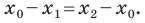

Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 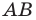
Пример №1
Докажите, что треугольник с вершинами в точках 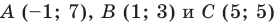
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
Следовательно, 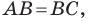
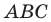
Поскольку 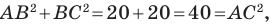
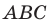
Пример №2
Точка 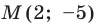
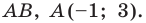
Решение:
Обозначим 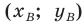
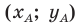
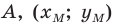
Поскольку 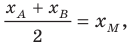
Аналогично
Ответ:
Пример №3
Докажите, что четырехугольник 
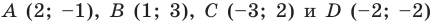
Решение:
Пусть точка 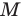
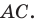
Следовательно,
Пусть точка 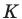
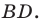
Следовательно,
Таким образом, точки 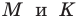
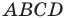
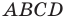
Найдем диагонали параллелограмма:
Следовательно, диагонали параллелограмма 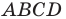
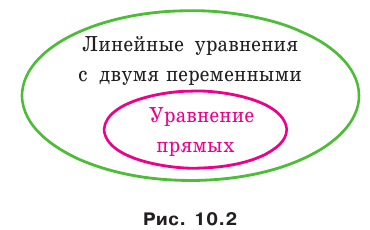
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 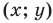
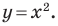
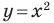
Определение. Уравнением фигуры 
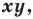
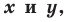
- если точка принадлежит фигуре
то ее координаты являются решением данного уравнения;
- любое решение
данного уравнения является координатами точки, принадлежащей фигуре
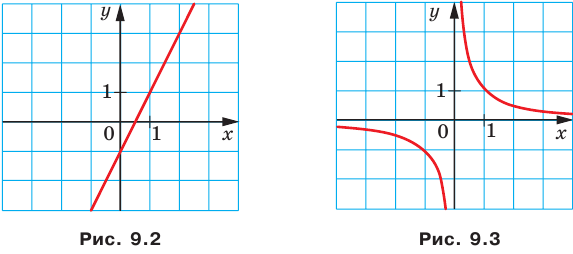
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 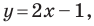
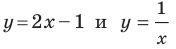
Если данное уравнение является уравнением фигуры 
Пользуясь этими соображениями, выведем уравнение окружности радиуса 
Пусть 
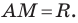
Отсюда
Мы показали, что координаты 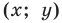
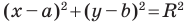
Пусть пара чисел 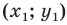
Тогда 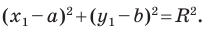
Это равенство показывает, что точка 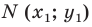
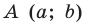
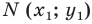
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 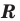
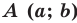
Верно и такое утверждение: любое уравнение вида 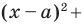
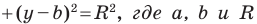
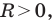
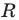
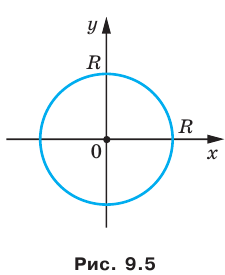
Если центром окружности является начало координат (рис. 9.5), то 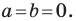
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 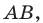
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 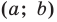
Следовательно,
Радиус окружности 
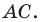
Следовательно, искомое уравнение имеет вид
Ответ:
Пример №5
Докажите, что уравнение 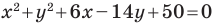
Решение:
Представим данное уравнение в виде
Следовательно, данное уравнение является уравнением окружности с центром в точке 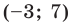
Ответ:
Пример №6
Докажите, что треугольник с вершинами в точках 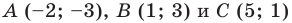
Решение:
Найдем квадраты сторон данного треугольника:
Поскольку 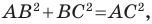
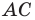
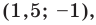
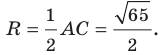
Ответ:
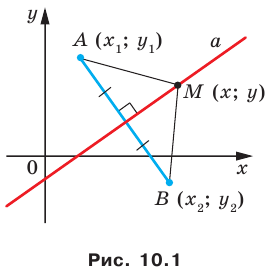
Уравнение прямой
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть 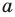
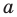
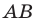
Пусть 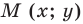
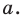
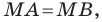
Мы показали, что координаты 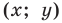
Теперь покажем, что любое решение уравнения 
Пусть 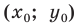
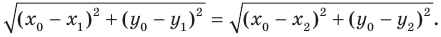
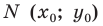
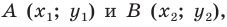
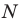
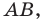
Итак, мы доказали, что уравнение 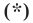
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 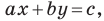
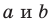
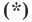
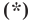
Раскроем скобки и приведем подобные слагаемые. Получим:
Обозначив 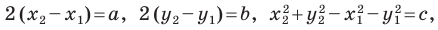
Поскольку точки 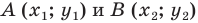
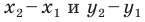
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где 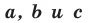
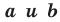
Верно и такое утверждение: любое уравнение вида 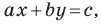
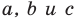
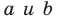
Если 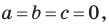
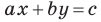
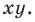
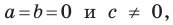
Из курса алгебры 7 класса вы знаете, что уравнение вида 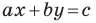
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 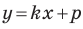
Перепишем уравнение 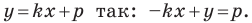
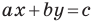
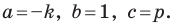
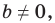
А любую ли прямую на плоскости можно задать уравнением вида 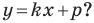
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой 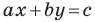
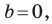
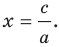
Если 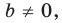
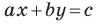
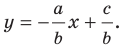
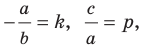
Следовательно, если 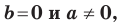
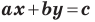
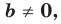
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.
Пример №7
Составьте уравнение прямой, проходящей через точки:
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 
2) Поскольку данные точки имеют разные абсциссы, то прямая 
Подставив координаты точек 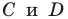
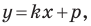
Решив эту систему уравнений, находим, что
Ответ:
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 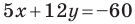
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 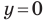
С осью ординат: при 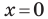
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 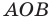
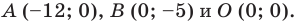
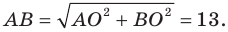
Ответ:
Угловой коэффициент прямой
Рассмотрим уравнение 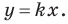
Покажем, что прямые 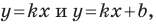
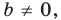
Точки 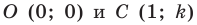
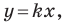
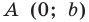
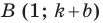
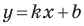
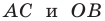
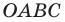
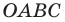
Теперь мы можем сделать такой вывод: если 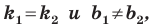
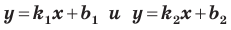
Пусть прямая 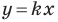
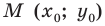
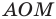
Если прямая 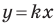
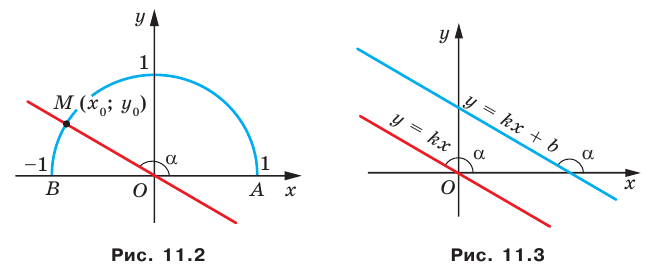
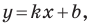
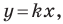
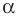
Рассмотрим прямую 
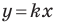
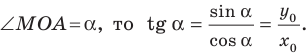
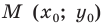
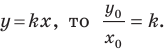
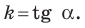
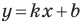
где 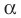
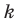
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 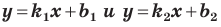
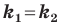
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 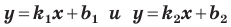
Пример №9
Составьте уравнение прямой, которая проходит через точку 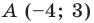
Решение:
Пусть уравнение искомой прямой 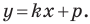
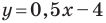
Следовательно, искомое уравнение имеет вид 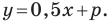
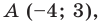
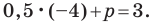
Искомое уравнение имеет вид
Ответ:
Метод координат
Мы часто говорим: прямая 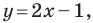
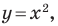
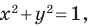
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
где числа 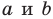
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
Отметим на плоскости две точки 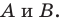
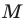
Это серединный перпендикуляр отрезка 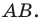
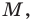
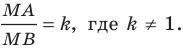
Плоскость, на которой отмечены точки 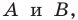
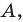
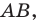
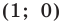
Пусть 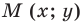
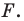
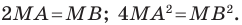
Следовательно, если точка 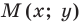
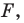
Пусть 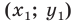
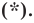
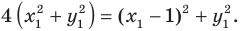
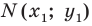
Таким образом, уравнением фигуры 
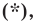
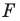
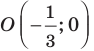
Мы решили задачу для частного случая, когда 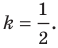
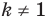
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 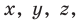
Справочный материал
Расстояние между двумя точками
Расстояние между точками 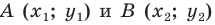
Координаты середины отрезка
Координаты 
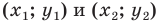
Уравнение фигуры
Уравнением фигуры 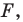
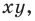
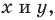
1) если точка принадлежит фигуре 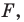
2) любое решение 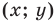
Уравнение окружности
Уравнение окружности радиуса 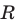
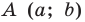
Любое уравнение вида 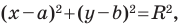
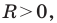
Уравнение прямой
Уравнение прямой имеет вид 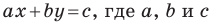
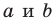
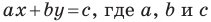
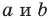
Если 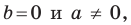
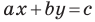
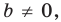
Угловой коэффициент прямой
Коэффициент 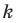
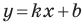
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 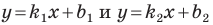
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
Доказательство.
Найдем длину
Найдем длину
A
=A
что и требовалось доказать
Ответ: а)АС=СВ
б)
в)
З
Дано:
Δ АВС;
А(0;0), В(3;1), С(1;7).
Доказать,
что Δ АВС прямоугольный.
адача №5.
В
А
С
Доказать, что треугольник с вершинами
А(0;0), В(3;1), С(1;7) прямоугольный.
Доказательство.
2)
.
Скалярное произведение ненулевых
векторов равно нулю тогда и только
тогда, когда эти вектора перпендикулярны.
Значит <В=90° , следовательно треугольник
АВС прямоугольный.
Что и требовалось доказать.
Задача №6.
Дано:
Δ АВС;
А(-2;1), В(4;8), С(10;6).
Доказать,
что Δ АВС тупоугольный.
А
В
С
Показать, что в треугольнике А(-2;1),
В(4;8), С(10,6) один угол тупой.
Доказательство.
2)
.
<B- тупой, так как скалярное
произведение двух векторов отрицательно
тогда и только тогда, когда между ними
тупой угол.
Ответ: Δ АВС тупоугольный.
З
Дано:
ABCD — параллелограмм;
А(4;2), В(4;8), С(10;6).
DA и СB –
диагонали
DACB=E
Найти:
а) D.
б) CB и DA.
в) E.
г)
CAB.
адача №7.
E
D
С
В
А
Даны
три вершины параллелограмма А(4;2), В(5;7),
С(-3;4)
а)
Найти координаты четвертой вершины D;
б)
Длины диагоналей AD и CB;
в)
Точку пересечения диагоналей E;
г)
Угол при вершине А.
Решение.
а) Известно, что диагонали параллелограмма
в точке пересечения делятся пополам.
Поэтому координаты точки E — пересечения
диагоналей — найдем как координаты
середины отрезка AC. Обозначая их через
получим,
что
.
E(1;
5,5)
Зная
координаты точки Е – середины диагонали
AD и координаты одного из
его концов А(4; 2), по формулам
где
х=1,
=4,
у=5,5,
=2,
получим
.
=-2
=9
D(-2;9).
б)
в) Найдем уравнения прямых содержащие
диагонали параллелограмма АD
и ВС по формуле
.
AD:
.
7х-28=-6у+12,
6у+7х-40=0.
ВС:
-3х+15=-8у+56,
8у-3х-41=0.
Найдем
точку пересечения прямых АD
и ВС:
.
=6(-3)-7
8=-18-56=-74;
=40
=-120-287=-407;
=40
320-246=74;
.
E(-1;
5,5) — точка пересечения диагоналей
г)
Найдем уравнение прямых АВ и АС по
формуле
.
представим уравнение в виде у=кх+в
АВ:
5х-20=у-2,
у=5х-18,
.
АС:
2х-8=-7у+14,
7у=-2х+22,
,
.
.
<A=arctg
Ответ: а) D(-2;9); б) BC=;
АD=;
в) Е(-1; 5,5); г)
САВ=arctg
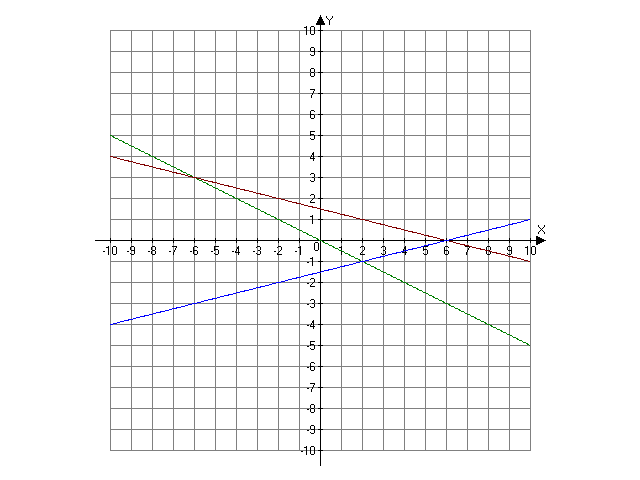
Задача
№8.
С
Дано:
AB: х+2у=0,
BC: х+4у-6=0;
AC: х-4у-6=0.
Найти
ВAС,
АBС,
ВCА.
А
В
Найти
внутренние углы треугольника, стороны
которого заданы уравнениями х+2у=0,
х+4у-6=0; х-4у-6=0.
Решение
x+2у=0,
х+4у-6=0, х-4у-6=0 распишем эти уравнения по
формуле у=кх+в
AB:
х+2у=0,
2у=-х,
.
ВС:
х+4у-6=0,
4у=-х+6,
.
AC:
х-4у-6=0,
4у=х-6,
BAC=180°-28°-12°30’=139°30′.
Ответ:
ABC=
12°30′;
BAC=28°;
BCA=139°30′.
Задача №9
Вычислить координаты вершин ромба, если
известны уравнения двух его сторон:
x+2y=4 и х+2у=10 и уравнение одной из его
диагоналей у=х+2
Дано:
Найти: А,В,С и D.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача 22351 4. Даны три последовательные вершины.
Условие
4. Даны три последовательные вершины параллелограмма: А(2;4;3), В(-3; 0; 6), С(-4; 2; 1). Найти уравнения стороны AD и диагонали BD.
Решение
Диагонали параллелограмма в точке пересечения делятся пополам.
Координаты точки М как середины диагонали АС:
x_(М)=(x_(A)+x_(C))/2
y_(М)=(y_(A)+y_(C))/2
z_(М)=(z_(A)+z_(C))/2
Подставляем координаты точек А и С и находим координаты точки М
х_(М)=(2-4))/2 ⇒ х_(М)=-1
у_(М)=(4+2)/2 ⇒ у_(М)= 3
z_(М)=(3+1)/2 ⇒ z_(М)= 2
Координаты точки М как середины диагонали BD:
x_(М)=(x_(B)+x_(D))/2
y_(М)=(y_(B)+y_(D))/2
z_(М)=(z_(B)+z_(D))/2
Подставляем координаты точки B и М и находим координаты точки D
-1=(-3+x_(D))/2 ⇒ х_(D)=1
3=(0+у_(D))/2 ⇒ у_(D)= 6
2=(6+у_(D))/2 ⇒ у_(D)= -2
Уравнение стороны AD, как прямой проходящей через две точки
Уравнение диагонали BD, как прямой проходящей через две точки
Найти четвертую вершину параллелограмма
Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?
В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.
Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.
Дано: ABCD — параллелограмм,
1) Найдём координаты точки O — середины диагонали AC.
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:
Дано: ABCD — параллелограмм,
1) Ищем координаты точки O — середины отрезка BD:
2) Точка O также является серединой AC:
2 Comments
А как вы получили -14 в первом примере.
Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.
Даны три последовательные вершины параллелограмма ABCD: А (2; 2), В (4;  и С (-6; 10). Напишите уравнение прямой AD
и С (-6; 10). Напишите уравнение прямой AD
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,296
- гуманитарные 33,622
- юридические 17,900
- школьный раздел 607,211
- разное 16,830
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
http://www.soloby.ru/1100489/%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5-%D0%B2%D0%B5%D1%80%D1%88%D0%B8%D0%BD%D1%8B-%D0%BF%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B0-%D0%BD%D0%B0%D0%BF%D0%B8%D1%88%D0%B8%D1%82%D0%B5-%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
:
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023

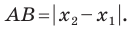
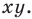
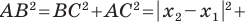
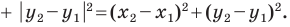

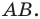
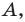

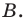
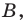
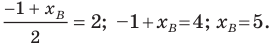
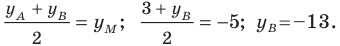
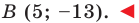
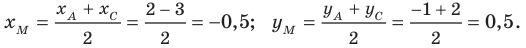
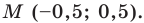
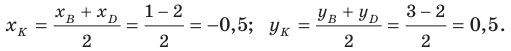
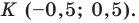
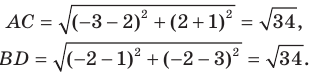

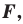 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;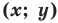 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре 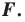
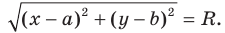
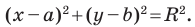
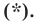
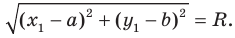
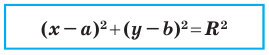
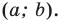
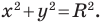
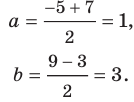
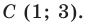
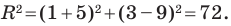
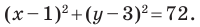
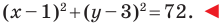
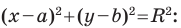
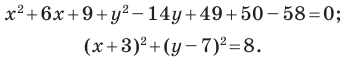
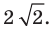
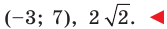
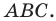
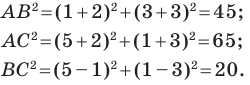
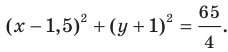
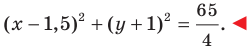
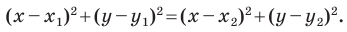
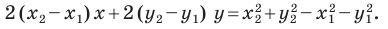
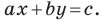
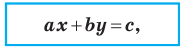
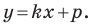
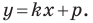
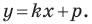


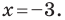
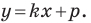
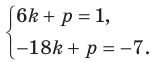
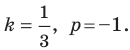
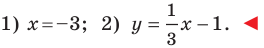
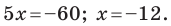
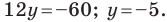
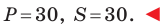
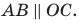
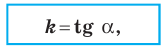
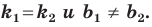
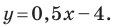
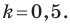
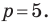
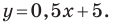
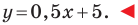
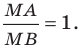
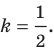
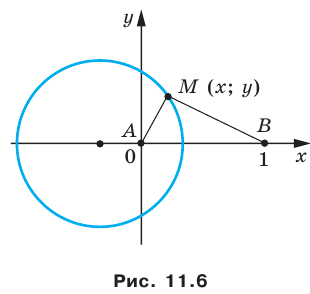
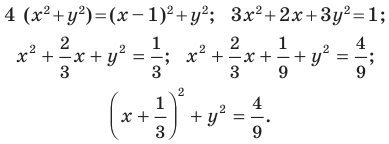
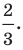
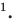
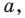

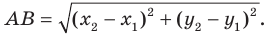
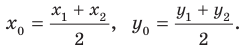
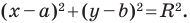
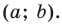
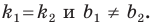









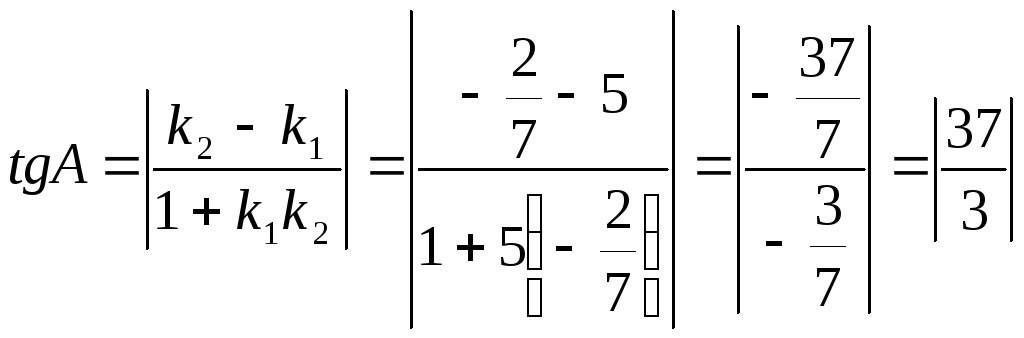

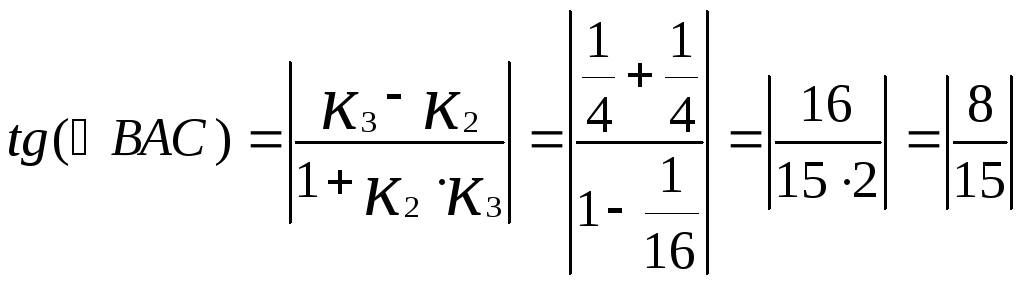
 и С (-6; 10). Напишите уравнение прямой AD
и С (-6; 10). Напишите уравнение прямой AD 












