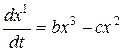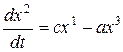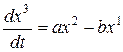Как найти координаты касательного вектора

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.

Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).

Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$

Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.

Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

Касательный вектор и касательное пространство к многообразию

Пусть на многообразии M задана кривая x = x(t) , a £ t £ b , где x – точка многообразия. Пока кривая находится в области U_p действия локальных координат , уравнения кривой можно записать в виде

.

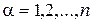
В этих координатах имеем вектор скорости кривой

.

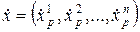
В области действия двух координатных систем U_p и U_q имеем две записи для уравнения кривой

и ,

.

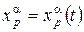
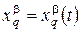
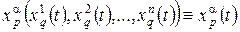
Дифференцируя это равенство получаем

.

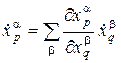
На основании этой формулы вводится следующее определение.

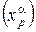
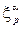
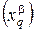
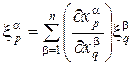
Определение 1. Касательным вектором к многообразию M в произвольной точке x называется вектор, записываемый в системе локальных координат набором чисел , который при переходе к другой системе координат преобразуется по закону

.

Касательные векторы к n-мерному многообразию M в данной точке x образуют n-мерное линейное пространство T_x = T_xM — касательное пространство.

В частности, вектор скорости любой гладкой кривой является касательным вектором.

Выбор локальных координат в окрестности точки x задает базис в касательном пространстве T_x .

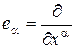
Гладкое отображение f многообразия M в многообразие N определяет индуцированное линейное отображение касательных пространств

При этом вектор скорости кривой x = x(t) на многообразии M переходит в вектор скорости кривой f(x(t)) на многообразии N.

В локальных координатах (x a ) в окрестности точки x и локальных координатах (y b ) в окрестности точки f(x) отображение f имеет вид

y b = f b (x 1 ,x 2 ,…,x n ), b = 1, 2, …, m ,

тогда индуцированное отображение f_* касательных пространств задается матрицей Якоби:

.

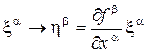
Векторное поле

Определение 1. Если в каждой точке x многообразия M определен вектор из соответствующего касательного пространства T_x, то говорят, что на многообразии задано векторное поле.

Для уточнения этого понятия отметим, что на множестве TM всех касательных пространств к многообразию M естественным образом вводится структура многообразия, картами которого служат прямые суммы карт многообразия M и касательных пространств к M в соответствующих точках многообразия M. Получаемое таким образом многообразие называется векторным расслоением многообразия M .Теперь векторное поле на многообразии M можно определить как отображение

такое, что y(x) Î T_xM для каждого x Î M.

Определение 2. Векторное поле называется гладким (класса C ¥ ), если отображение y является гладким.

В локальных координатах многообразия TM векторное поле имеет вид

. (2)

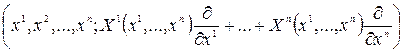
Определение 3. Векторной линией называется такая линия многообразия, в каждой точке которой вектор поля касается этой линии. Векторные линии также называются орбитами и интегральными кривыми векторного поля.

В локальных координатах векторная линия описывается следующей системой дифференциальных уравнений:

, i = 1,2,…,n ,

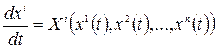
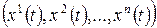
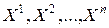
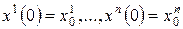
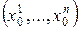
где — координатное задание искомой линии, а — координаты векторной части векторного поля. Граничным условием здесь является , где — координаты точки x_o.

Пример 1. В трехмерном евклидовом пространстве рассмотрим векторное поле

X 1 = bx 3 – cx 2 , X 2 = cx 1 — ax 3 , X 3 = ax 2 — bx 1 .

Система дифференциальных уравнений для нахождения векторной линии принимает вид

Умножим эти уравнения на x i соответственно и, сложив, получим

x 1 dx 1 + x 2 dx 2 + x 3 dx 3 = 0 dt = 0. (3)

Аналогично, умножая эти уравнения на a, b и c и складывая получим

adx 1 + bdx 2 + cdx 3 = 0. (4)

Интегрируя уравнения (3) и (4) получаем следующую систему уравнений

(5)

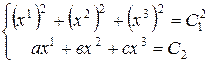
Из этой системы следует, что векторные линии рассматриваемого векторного поля получаются в результате пересечения всевозможных концентрических сфер с центрами в начале координат со всевозможными плоскостями перпендикулярными вектору (a,b,c), то есть, векторные линии данного векторного поля являются окружностями с центрами на прямой, проходящей через начало координат и имеющей направляющим вектором вектор (a,b,c) и лежащими в плоскостях перпендикулярных этой прямой.

Отметим, что рассмотренное векторное поле является полем скоростей точек твердого тела, вращающегося вокруг описанной выше прямой с постоянной угловой скоростью.

Кинематика материальной точки

Основные формулы кинематики материальной точки

Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.

Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz :
,
где – единичные векторы (орты) в направлении осей x, y, z .

Скорость точки:
;
;
;
Единичный вектор в направлении касательной к траектории точки:
.
Вектор можно выбрать двумя способами во взаимно противоположных направлениях. Обычно его выбирают в направлении увеличения дуговой координаты. Тогда, наряду с модулем скорости , вводят алгебраическую величину скорости . При , вектор скорости сонаправлен с . При – имеет противоположное с направление.

Скорость и ускорение точки M

Тангенциальное (касательное) ускорение:
;
;
.
Здесь, как и для скорости, – это алгебраическое касательное ускорение, . Если , то вектор касательного ускорения сонаправлен с . При – имеет противоположное с направление.

Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.

Радиус кривизны траектории:
.

Далее приводится вывод этих формул и изложение теории кинематики материальной точки.

Радиус-вектор и траектория точки

Рассмотрим движение материальной точки M . Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O . Тогда положение точки M однозначно определяются ее координатами ( x, y, z ) . Эти координаты являются компонентами радиус-вектора материальной точки.

Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M .
,
где – единичные векторы в направлении осей x, y, z .

При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.

Траектория материальной точки – это линия, вдоль которой происходит движение точки.

Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями

В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .

Скорость материальной точки

Согласно определению скорости и определению производной:

Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:

,
где
,
,

– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.

Таким образом
.
Модуль скорости:
.

Касательная к траектории

С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.

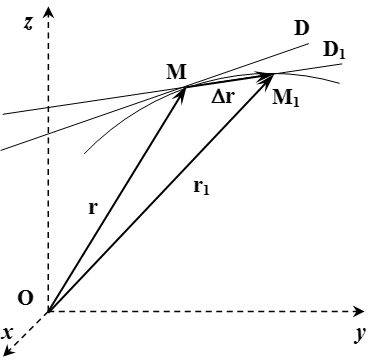
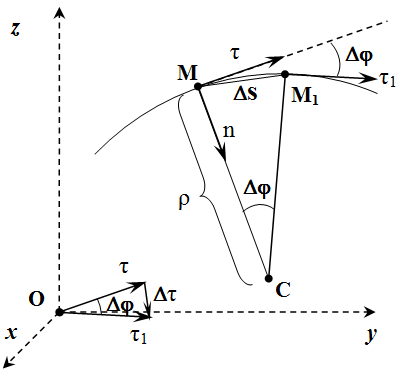
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .

При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.

Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.

Здесь мы направили вектор по направлению к вектору скорости, поскольку это более удобно. Но могут возникнуть случаи, когда точка останавливается и движется по той же траектории в обратном направлении. Чтобы не вводить для одной и той же точки траектории два единичных касательных вектора, нужно охватить случай, когда направлен противоположно скорости. Для этого вводят алгебраическую величину скорости:
.
Если направления векторов и совпадают, то . Если они противоположны, то .
– это проекция скорости на направление единичного вектора . Она равна скалярному произведению этих векторов:
.

Абсолютную величину (модуль) вектора скорости мы обозначаем символом с прямыми скобками, или символом без стрелки:
;
Алгебраическая величина скорости:
.

Тогда вектор скорости точки можно представить в следующем виде:
.

Ускорение материальной точки

Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.

Тангенциальное (касательное) и нормальное ускорения

Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.

Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?

Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают их скалярное произведение. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.

Скорость, касательное и нормальное ускорение точки M

Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к ней.

Тангенциальное (касательное) ускорение

Также как и для скорости, введем алгебраическую величину вектора касательного ускорения :
.
Если , то вектор касательного ускорения сонаправлен с . Если , то эти векторы противоположны. Абсолютную величину касательного ускорения будем обозначать прямыми скобками: . Тогда
.

Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили: .
Отсюда видно, что алгебраическая величина тангенциального ускорения равна проекции полного ускорения на направление касательной к траектории. Она также равна производной по времени алгебраической величины скорости точки: .

Подставив , имеем:
.
Здесь мы учли, что .

Найдем производную по времени модуля скорости . Применяем правила дифференцирования:

;
.

Итак,
.
Отсюда следует, что если между векторами ускорения и скорости острый угол: , то движение ускоренное. Абсолютное значение скорости возрастает. Если между ними тупой угол: , то движение замедленное. Абсолютное значение скорости убывает.

Выразим ускорение через тангенциальное и нормальное: , и учтем, что . Получим:
.
Тогда предыдущую формулировку можно выразить посредством тангенциального ускорения. Если векторы касательного ускорения и скорости направлены в одну сторону, то движение ускоренное. Если их направления противоположны, то движение замедленное.

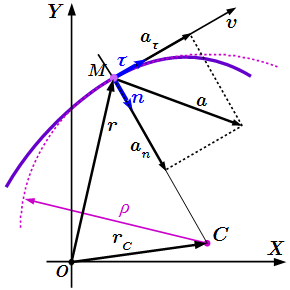
Радиус кривизны траектории

Теперь исследуем вектор .

Рассмотрим вектор в два момента времени – в момент времени t и в момент t ₁ . Введем обозначения: . По определению производной:
.
Пусть в момент времени t , точка находится в положении M , а в момент t ₁ – в положении M ₁ (см. рисунок).

Рассмотрим случай, когда алгебраическая скорость положительна: . То есть направления векторов и совпадают. Тогда точка M ₁ находится справа от M . Через точки и проведем плоскости, перпендикулярные векторам и . Пересечение этих плоскостей образует прямую. Она проходит через точку C перпендикулярно плоскости рисунка. MC – это перпендикуляр, опущенный из точки M на эту прямую.

При , точка стремится к точке , а длина отрезка CM стремится к радиусу кривизны траектории ρ . Поскольку и , то угол между отрезками и равен углу между векторами и . Отложим их для наглядности из одного центра.

Абсолютное значение производной:
.
Здесь мы учли, что .

Вектор , как указывалось выше, перпендикулярен . В данном случае он направлен вдоль единичного вектора главной нормали , направленной к центру кривизны C траектории. Поэтому при имеем:
.

Теперь рассмотрим случай, когда алгебраическое значение скорости отрицательно: . В этом случае, вектор скорости противоположен . Получается тот же рисунок, только точка располагается слева от M . В результате абсолютное значение производной остается прежней:
.
Но ее направление меняется на противоположное:
.
Поскольку , то формула сохраняет прежний вид и в этом случае:
.

Нормальное ускорение

Теперь находим нормальное ускорение:
.
Перепишем результат в следующем виде:
,
где ; – единичный вектор в направлении главной нормали траектории – то есть вектор, направленный к мгновенному центру кривизны перпендикулярно касательной к траектории. Поскольку , то также является модулем нормального ускорения. Для него не нужно вводить алгебраическое значение, как мы это делали для скорости и касательного ускорения.
Нормальное ускорение всегда направлено к центру кривизны траектории.

Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.

Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.

Выпишем еще раз следующую формулу:
.
Отсюда видно, что нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.

Радиус кривизны траектории:
.

И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.

Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.

Автор: Олег Одинцов . Опубликовано: 09-02-2016 Изменено: 27-01-2020

, ξ n и η 1 , . . . , η n соответственно, их линейной комбинацией aξ + bη считаетсявектор, задаваемый числами aξ i + bη i , i = 1, . . . , n.Задача 1. Доказать, что сумма векторов и произведение вектора на число не зависят отиспользованной системы координат.Задача 2. Определить сумму и произведение на число касательных векторов, понимаемыхкак классы касающихся кривых.Пусть в окрестности точки P задана система координат x1 , . . . , xn ; в касательномпространстве TP M рассмотрим базис e1 , . . . , en , состоящий из векторов, которые задаютсяв данной систем координат наборами чисел eij = δji .Определение 11. Этот базис называется каноническим базисом, соответствующим системекоординат x1 , . .

. , xn .Ясно, что базисный вектор ej — это вектор скорости к j–й координатной линии, т.е.кривой вида xi = xi0 , i 6= j, xj = xj0 + t, проходящей через точку P (здесь xi0 — координатыэтой точки). Числа, сопоставленные касательному вектору в данной системе координат —это его координаты в соответствующем каноническом базисе.

При замене координат канонический базис меняется; матрица перехода от одного канонического базиса к другому —это в точности матрица Якоби замены координат (докажите!); формула (1) — это законпреобразования координат вектора при замене базиса.Помимо двух описанных способов определения касательного вектора существует ещетретий способ — определить этот вектор при помощи операции дифференцирования вдольнего. Именно, рассмотрим всевозможные гладкие функции на M, определенные в некоторой окрестности точки P и пусть ξ ∈ TP M — касательный вектор. Рассмотрим произвольную проходящую через P кривую γ, для которой ξ является вектором скорости, иограничим гладкую функцию f на эту кривую, т.е.

рассмотрим гладкую функцию f ◦ γодной переменной t: f ◦ γ(t) = f (γ(t)), t ∈ [a, b]. Будем считать, что кривая γ проходитчерез точку P при t = t0 .Определение 12. Производной функции f вдоль касательного вектора ξ в точке P называется число:d ∂ξ (f ) = f (γ(t)).dt t=t0Утверждение 2. Приведенное определение корректно, т.е. не зависит от выбора кривой γ,представляющей касательный вектор ξ.94Доказательство.

В локальных координатах x1 , . . . , xn функция f — это обычная гладкая функция n переменных f (x1 , . . . , xn ). Кривая γ задается уравнениями xi = xi (t), акасательный вектор ξ — координатным набором чисел ξ 1, . . . , ξ n :ξi =Отсюда находим:dxi .dt t=t0nnXXd ∂fdxj ∂f1n∂ξ (f ) = f (x (t), . . .

, x (t)) =(P )(P )ξ j . =jjdt t=t0∂xdt t=t0 j =1 ∂xj =1Последнее выражение зависит только от функции f и вектора ξ.Таким образом каждый касательный вектор определяет отображение множествагладких функций, заданных в окрестности P , в числа (каждой функции сопоставляетсяее производная вдоль этого вектора), причем это отображение удовлетворяет очевиднымсвойствам:1. ∂ξ (af + bg) = a∂ξ (f ) + b∂ξ (f ),a, b ∈ R (линейность),2.

∂ξ (f g) = f (P )∂ξ (f ) + g(P )∂ξ (f ) (правило Лейбница).Определение 13. Отображение множества гладких функций на M в числа, удовлетворяющее условием 1), 2) называется дифференцированием множества функций на M вточке P .Ясно, что каждый касательный вектор из TP M определяет единственное дифференцирование. Оказывается, это соответствие взаимно–однозначно.Теорема 1. Для каждого дифференцирования A множества гладких функций на M вточке P найдется единственный вектор ξ ∈ TP M, для которого:A(f ) = ∂ξ (f ).Доказательство. Зафиксируем систему координат x1 , . . .

, xn в окрестности точки P и рассмотрим произвольную гладкую функцию f . Из формулы Тейлора следует, что в окрестности точки P эта функция представляется в виде:f = f (P ) +nnXX∂fjj(P)(x−x)+hj (x)(xj − xj0 ),0j∂xi =1i, j =1где xi0 — координаты точки P , а hj (x) — гладкие функции, причем hj (P ) = 0 (докажите!).Применим к этой функции отображение дифференцирования A; пользуясь линейностью,получим:nnXX∂fjjA(f ) = f (P )A(1) +(P )A(x − x0 ) + A(hj (x)(xj − xj0 )).j∂xj =1i, j =1Из правила Лейбница следует, что A(1) = A(1 • 1) = A(1) + A(1), откуда A(1) = 0; крометого, из того же правила следует, что:A(nXi, j =1hj (x)(xj − xj0 )) = 095(каждое слагаемое в этой сумме представлено в виде произведения двух функций, каждаяиз которых обращается в нуль в точке P ).

Обозначая ξ i = A(xi − xi0 ), получим:A(f ) =nX∂f(P )ξ j = ∂ξ (f ),j∂xi =1где ξ — касательный вектор, заданный в системе координат x1 , . . . , xn числами ξ 1 , . . . , ξ n .Докажем, что вектор ξ единственный. Действительно, из равенства ∂ξ (f ) = ∂η (f ) следует,что:nX∂f j(ξ − η j ) = 0,j∂xj =1которое должно быть выполнено для любой гладкой функции f .

Выбирая f = xk ,k = 1, . . . , n получим ξ k = η k , т.е. ξ = η.Таким образом, мы приходим к третьему определению касательного вектора.Определение 14. Касательным вектором в точке P к многообразию M называется дифференцирование множества гладких функций на M в точке P .Ясно, что при фиксированной системе координат x1 , . .

. , xn дифференцирование, соответствующее вектору ej канонического базиса — это дифференцирование по локальнойкоординате xj :∂f∂ej (f ) = j .∂xПоэтому для этого вектора часто используется обозначение ∂/∂xj ; таким образом, канонический базис, порожденный в касательном пространстве координатами x1 , .

. . , xn , состоитиз векторов:∂∂,…,,∂x1∂xnа каждый касательный вектор ξ имеет вид:ξ=nXξjj =196∂.∂xjЗадачи.1. Построить атлас:(a) на окружности;(b) на сфере;(c) на цилиндре(d) на торе.2. Доказать, что множество M, заданное в трехмерном пространстве уравнением F (x, y, z) = 0,причем ∇F |M 6= 0, является многообразием. Найти его размерность.3. Доказать, что множество M, заданное в n–мерном пространстве системой уравнений:F1 (x1 , . .

. , xn ) = 0, . . . , Fk (x1 , . . . , xn ) = 0,причем ранг матрицы Якоби ∂Fi /∂xj во всех точках M равен k, является многообразием. Найти его размерность.4. Доказать, что проективная прямая (множество прямых на плоскости, проходящихчерез начало координат) — многообразие. Найти его размерность.5.

Доказать, что проективная плоскость (множество прямых в трехмерном пространстве, проходящих через начало координат) — многообразие. Найти его размерность.6. Доказать, что следующие матричные группы являются многообразиями и найти ихразмерности:(a) SL(2,R) — 2 × 2-матрицы с определителем 1,(b) SO(2) — 2 × 2 ортогональные матрицы с определителем 1,(c) SU(2) — 2 × 2 унитарные матрицы с определителем 1,(d) SL(n,R) — n × n-матрицы с определителем 1,(e) T(n,R) — верхнетреугольные n × n-матрицы,(f) SO(3) — 3 × 3 ортогональные матрицы с определителем 1,λ 0(g)λ > 0, a > 0 − фиксировано.0 λa7. Доказать, что прямое произведение конечного числа многообразий — многообразие.Найти его размерность.8.

Найти касательные пространства к многообразиям из задач 2,3,6.9. Доказать, что следующие матричные группы являются многообразиями, найти ихразмерности и касательные пространства в единице:(a) SL(n,R),(b) SO(n),(c) SU(n).9710. Найти касательное пространство к группе SO(3) в точке:√1/23/20√A =  − 3/2 1/2 0  .00111. Найти координату единичного вектора, касающегося окружности радиуса R точкеϕ = π/3 в системе координат “полярный угол” и в координате стереографическойпроекции.12. Найти координаты касательного вектора к образующей и параллели на конусе вкоординатах: (r, ϕ), (z, ϕ), (x, y).13. На цилиндре найти координаты вектора, касающегося винтовой линии с шагом d, вцилиндрических координатах (ϕ, z).√14.

На цилиндре найти координаты касательного вектора (−R 3, R, 1) в точке ϕ = π/3,z = 1 в цилиндрических координатах (ϕ, z) и в координатах стереографической проекции.√√√ √15. На сфере найти координаты касательного вектора (− 2, 2, 1) в точке (1/ 2, 1/ 2, 0)в сферических координатах и в координатах стереографической проекции.16. То же для вектора, касающегося:(a) меридиана;(b) параллели;(c) большого круга, лежащего в плоскости x + 3y − 2z = 0.17. На проективной плоскости (множестве прямых в R3 ) найти координаты в аффинныхкартах касательного вектора в точке t = π/4 к кривой r = (cos t, sin t, t).18.

Доказать, что для всякого многообразия M его касательное и кокасательное расслоения являются многообразиями. Найти их размерность. Поясним, что касательноерасслоение к многообразию M — это множество пар вида (P, ξ), где P — точка многообразия M, а ξ — касательный вектор к M в этой точке; кокасательное расслоениеобразовано парами (P, α), где α — линейный функционал на касательном пространстве TP M.9814 Лекция 14. Вложения и погружения многообразий§ 1. Дифференциал гладкого отображения.Выше мы видели, что гладкое отображение поверхностей индуцирует отображениекасательных векторов к ним: вектор скорости некоторой кривой на первой поверхности переходит в вектор скорости образа этой кривой (в соответствующей точке) на второй поверхности.

Точно так же обстоит дело и в случае произвольных многообразий.Именно, пусть M, Q — гладкие многообразия размерностей n, m соответственно, и пустьf : M → Q — гладкое отображение. Рассмотрим произвольный касательный вектор ξ кмногообразию M в точке P . Это — класс касающихся в точке P гладких кривых на M;пусть γ — одна из кривых (представитель) этого класса.

Отображение f переводит этукривую в гладкую кривую f (γ), лежащую на многообразии Q и проходящую через точкуf (P ); обозначим через dP f (ξ) вектор скорости кривой f (γ) в этой точке.Теорема 1. Вектор dP f (ξ) не зависит от выбора кривой γ из класса, определяющеговектор ξ; таким образом, описанная конструкция корректно определяет отображениеdP f : TP M → Tf (P ) Q.

From Wikipedia, the free encyclopedia

For a more general, but more technical, treatment of tangent vectors, see Tangent space.

In mathematics, a tangent vector is a vector that is tangent to a curve or surface at a given point. Tangent vectors are described in the differential geometry of curves in the context of curves in Rⁿ. More generally, tangent vectors are elements of a tangent space of a differentiable manifold. Tangent vectors can also be described in terms of germs. Formally, a tangent vector at the point is a linear derivation of the algebra defined by the set of germs at .

Motivation[edit]

Before proceeding to a general definition of the tangent vector, we discuss its use in calculus and its tensor properties.

Calculus[edit]

Let be a parametric smooth curve. The tangent vector is given by , where we have used a prime instead of the usual dot to indicate differentiation with respect to parameter t.^[1] The unit tangent vector is given by

Example[edit]

Given the curve

in , the unit tangent vector at is given by

Contravariance[edit]

If is given parametrically in the n-dimensional coordinate system xⁱ (here we have used superscripts as an index instead of the usual subscript) by or

then the tangent vector field is given by

Under a change of coordinates

the tangent vector in the uⁱ-coordinate system is given by

where we have used the Einstein summation convention. Therefore, a tangent vector of a smooth curve will transform as a contravariant tensor of order one under a change of coordinates.^[2]

Definition[edit]

Let be a differentiable function and let be a vector in . We define the directional derivative in the direction at a point by

The tangent vector at the point may then be defined^[3] as

Properties[edit]

Let be differentiable functions, let be tangent vectors in at , and let . Then

Tangent vector on manifolds[edit]

Let be a differentiable manifold and let be the algebra of real-valued differentiable functions on . Then the tangent vector to at a point in the manifold is given by the derivation which shall be linear — i.e., for any and we have

Note that the derivation will by definition have the Leibniz property

See also[edit]

• Differentiable curve § Tangent vector
• Differentiable surface § Tangent plane and normal vector

References[edit]

Bibliography[edit]

• Gray, Alfred (1993), Modern Differential Geometry of Curves and Surfaces, Boca Raton: CRC Press.
• Stewart, James (2001), Calculus: Concepts and Contexts, Australia: Thomson/Brooks/Cole.
• Kay, David (1988), Schaums Outline of Theory and Problems of Tensor Calculus, New York: McGraw-Hill.

Для более общей, но более технической обработки касательных векторов см. Касательное пространство .

В математике , А касательный вектор представляет собой вектор , который является касательной к кривой или поверхности в данной точке. Касательные векторы описываются в дифференциальной геометрии кривых в контексте кривых в R ⁿ . В более общем смысле , касательные векторы являются элементами касательного пространства в виде дифференцируемого многообразия . Касательные векторы также можно описать в терминах ростков . Формально касательный вектор в точке является линейным производным алгебры, определяемой множеством ростков в точке .

Мотивация

Прежде чем перейти к общему определению касательного вектора, мы обсудим его использование в исчислении и его тензорные свойства.

Исчисление

Позвольте быть параметрической гладкой кривой . Касательный вектор задается как , где мы использовали штрих вместо обычной точки для обозначения дифференцирования по параметру t . Единичный касательный вектор задается формулой

Пример

Учитывая кривую

в единичный касательный вектор в задается формулой

Контравариантность

Если задано параметрически в n -мерной системе координат x ⁱ (здесь мы использовали верхние индексы в качестве индекса вместо обычного нижнего индекса) посредством или

то касательное векторное поле задается формулой

При смене координат

касательный вектор в u ⁱ -системе координат задается формулой

где мы использовали соглашение Эйнштейна о суммировании . Следовательно, касательный вектор гладкой кривой при изменении координат преобразуется в контравариантный тензор первого порядка.

Определение

Позвольте быть дифференцируемой функцией и пусть быть вектором в . Определим производную по направлению в точке как

Касательный вектор в точке может быть определен как

Характеристики

Позвольте быть дифференцируемыми функциями, пусть быть касательными векторами в at , и пусть . потом

Касательный вектор на многообразиях

Пусть — дифференцируемое многообразие и пусть — алгебра вещественнозначных дифференцируемых функций на . Тогда касательный вектор к в точке на многообразии задается дифференцированием, которое должно быть линейным, т. Е. Для любого, и мы имеем

Обратите внимание, что вывод по определению будет обладать свойством Лейбница

Смотрите также

• Дифференцируемая поверхность # Касательная плоскость и вектор нормали

использованная литература

Библиография

• Грей, Альфред (1993), Современная дифференциальная геометрия кривых и поверхностей , Бока-Ратон: CRC Press.

• Стюарт, Джеймс (2001), Исчисление: концепции и контексты , Австралия: Томсон / Брукс / Коул.
• Кей, Дэвид (1988), Обзор теории и проблем тензорного исчисления Шаумсом , Нью-Йорк: МакГроу-Хилл.