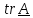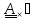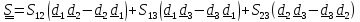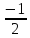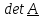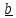Как найти координату в тензоре - Avtoru.top - решение различных проблем

Будем (для простоты)
использовать ортонормированный базис
,которого
вполнедостаточно для изложения основных
понятий в курсе теоретической механики,
тем более что все формулы остаются
справедливыми и в случае произвольного
базиса.

Разложим все
векторы в произвольном тензоре
по базису:

,
, подставим ви «приведем подобные». Получим

,
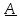
где набор из девяти диад

называется
тензорным

базисом, а величины
—
координатами (компонентами) тензора.

Тензору
в указанном базисе можно сопоставить
матрицу=.

Подчеркнем, что
матричный образ тензора изменяется при
изменении системы координат, а
следовательно и базиса, а сам тензор —
нет; в этом и заключается, пожалуй,
главное ( но не единственное) преимущество
тензорного «языка».

3. Скалярное и векторное умножение тензора на вектор и тензор. Единичный тензор.

Скалярное
произведение – самая распространенная
операция. Пусть
.

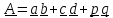
По определению,
умножение справа:
)
=,

умножение
слева:
=.

В обоих случаях
вектор скалярно умножается на ближайший
в каждой диаде вектор, и в результате
получается новый вектор; отсюда,
по-видимому, следует принятое в математике
определение тензора как « линейного
оператора, преобразующего векторное
пространство само в себя». Впрочем, и
это крайне узкое определение имеет
смысл.

Пусть тензор –
одна диада
.
Тогда при умножении его, например,
справа на любой векторполучается– вектор, коллинеарный вектору— отсюда и его название «линейный тензор».
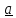
Если– сумма двух диад, то при умножении

его (например)
справа на любой вектор
получится вектор,
лежащий в плоскости векторови–отсюда и название «плоский тензор»:
все векторы «ложатся» на одну плоскость.

Аналогично
умножению на вектор вводится скалярное
умножение тензора на тензор.

Пусть
,.
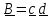
Тогда()— новый тензор.

Правило осталось
тем же: скалярно перемножаются ближайшие
векторы в диадах.

Упражнение:
1.Показать, что
и, следовательно для симметричного

тензора
, а для кососимметричного ()

2.
Показать, что

Пусть тензоры
записаны в координатном виде
,.

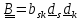
Тогда
,

откуда изполучаем правило перемножения матриц
,которое в

линейной алгебре
вводится «по определению».

Единичным тензором
называется тензор, в результате
скалярного произведения на который
слева или справа вектора ( или тензора)
получается тот же самый вектор (или
тензор.)

Разложение
вектора
по базису имеет вид=
(, где,

согласно определению,

— единичный тензор

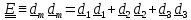
Обратным к тензору.называется тензор,являющийся
решением уравнения

.или, что равносильно,.

Векторное
умножение тензора на вектор достаточно
показать на одной диаде

— получается новый
тензор.

Упражнение.
Доказать тождество
,
( 1.7)

и, умножив его
скалярно на
,
получить формулу (1.6) двойного векторного
произведения.

4.След, векторный инвариант, определитель тензора. Теорема о представлении кососимметричного тензора .

След (trace)
тензора
—
число, получаемое заменой диадного

умножения на
скалярное:

(1.8)

Если тензор записан
в координатном виде
,
то— сумма

элементов главной
диагонали матрицы. В силу своего
определения при любой замене базиса
след тензора не изменяется (скалярные
произведения от базиса не зависят),
поэтому его называют первым
инвариантом
тензора.

Векторным
инвариантом тензора
называется вектор, полученный заменой
диадного произведения векторным:

или
(1.9)

Векторный инвариант
симметричного тензора, у которого
равен нулю.

Что же касается
кососимметричного тензора, то можно
доказать теорему:

Теорема.
Произвольный
кососимметричный тензор
может быть
единственным

образом
представлен
в виде

, (1.10)

где
называется
сопутствующим вектором тензора
.

Доказательство.
Поскольку
,
то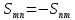иможем записать в виде

Найдем вектор

и обозначим его
:.

Поскольку
координаты
содержат по одной лишь компоненте
тензора,
а не их

комбинации, то
сопутствующий вектор определяется
через
единственным образом.

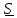
Обратно, умножив

,
убедимся, что.

Определителем
(детерминантом) тензора называется
число:

,
(1.11)

Очевидно, что
определение (1.11) не зависит от системы
координат и, более того, можнодоказать,
что оно не зависит и от выбора тройки
некомпланарных векторов
.
Запишем тензор в видеи
обозначим для простоты.Тогда

и с помощью (1.5)
выражение (1.11) принимает вид определителя
матрицы координат тензора в ортонормированном
базисе:

(1.12)

Определитель
тензора имеет простой геометрический
смысл. Обозначим
,

,
.
Тогда, вспомнив, что смешанное произведение
– объем построенного на перемножаемых
векторах параллелепипеда, получим:-отношение

«деформированного
и повернутого» объема к исходному.

Соседние файлы в предмете Теоретическая механика

Источник

а затем берем числа перед членами как координаты.

Здесь я написал бы «числа перед членами ». Эти числа и есть координаты тензора в базисе , по определению.

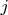
Так как векторных множителей здесь всего два, можно условиться записывать коэффициенты $c^{ij}$ в виде матрицы для наглядности ( $i$ , как обычно, — это номер строки, $j$ — номер столбца). У меня получилось:
а) $begin{bmatrix}1&-1\1&-1end{bmatrix}$
б) $begin{bmatrix}1&1\1&1end{bmatrix}$
в) $begin{bmatrix}1&1&0\2&2&0\0&0&0end{bmatrix}-begin{bmatrix}1&0&2\1&0&2\0&0&0end{bmatrix}=begin{bmatrix}0&1&-2\1&2&-2\0&0&0end{bmatrix}$
И вот этот тензор (как и подавляющее большинство тензоров) уже невозможно представить в виде тензорного произведения двух векторов, а только в виде суммы таких произведений. Это то, что автор задачи хочет, чтобы решающие поняли.
г) $begin{bmatrix}0&0&1&1\0&0&2&2\0&0&0&0\0&0&0&0end{bmatrix}-begin{bmatrix}0&0&1&-1\0&0&-2&2\0&0&0&0\0&0&0&0end{bmatrix}=begin{bmatrix}0&0&0&2\0&0&4&0\0&0&0&0\0&0&0&0end{bmatrix}$
Всё совпадает с Вашими решениями, которые получаются, если элементы этих матриц выписать построчно.

(Кстати)

Матричная запись координат оправдывается не только удобством. Сам тензор можно получить из такой формальной записи:
$begin{bmatrix}e_1&e_2&e_3end{bmatrix}otimesbegin{bmatrix}c^{11}&c^{12}&c^{13}\c^{21}&c^{22}&c^{23}\c^{31}&c^{32}&c^{33}end{bmatrix}begin{bmatrix}e_1\e_2\e_3end{bmatrix}$
Знак тензорного произведения можно было бы поставить справа от матрицы. Раскрывая это по правилам матричного умножения, получим нужную сумму из девяти (в этом примере) слагаемых $c^{ij}e_iotimes e_j$ . Я пишу в ответах только центральную матрицу, потому что в задании надо найти координаты.

Теперь можно приступить и к более сложному заданию 1. Там получается тензор аж пятого ранга, вида $c_{ijkell m}e^iotimes e^jotimes e^kotimes e^ellotimes e^m$ (пять знаков суммирования подразумеваются). Вот Вам и надо найти $c_{12333}$ , то есть коэффициент при .
Не все мои обозначения (различение верхних и нижних индексов, матричная запись коэффициентов, соглашение Эйнштейна) могут понравиться Вашему преподавателю, так что Вы осторожнее.

Источник

Время на прочтение
7 мин

Количество просмотров 315K

Содержание

Что такое тензор и для чего он нужен?
Векторные и тензорные операции. Ранги тензоров
Криволинейные координаты
Динамика точки в тензорном изложении
Действия над тензорами и некоторые другие теоретические вопросы
Кинематика свободного твердого тела. Природа угловой скорости
Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
О свертках тензора Леви-Чивиты
Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
Получаем вектор угловой скорости. Работаем над недочетами
Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
Параметры Родрига-Гамильтона в кинематике твердого тела
СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
Нестандартное введение в динамику твердого тела
Движение несвободного твердого тела
Свойства тензора инерции твердого тела
Зарисовка о гайке Джанибекова
Математическое моделирование эффекта Джанибекова

Введение

Это было очень давно, когда я учился классе в десятом. Среди довольно скудного в научном плане фонда районной библиотеки мне попалась книга — Угаров В. А. «Специальная теория относительности». Эта тема интересовала меня в то время, но информации школьных учебников и справочников было явно недостаточно.

Однако, книгу эту я читать не смог, по той причине, что большинство уравнений представлялись там в виде тензорных соотношений. Позже, в университете, программа подготовки по моей специальности не предусматривала изучение тензорного исчисления, хотя малопонятный термин «тензор» всплывал довольно часто в некоторых специальных курсах. Например, было жутко непонятно, почему матрица, содержащая моменты инерции твердого тела гордо именуется тензором инерции.

Погружение в специальную литературу не приносило просветления. Технарю достаточно тяжело переварить строгий абстрактный язык чистой математики. Тем не менее, от случая к случаю я возвращался к этому вопросу, и вот спустя почти шестнадцать лет наступило просветление, о чем и будет рассказано под катом. Возможно, мои рассуждения покажутся примитивными и упрощенными, но понимание любой сложной вещи принято разворачивать от процесса оперирования простыми понятиями, поэтому начнем.

1. Вектор на плоскости. Контравариантные, ковариантные координаты и связь между ними

Рассмотрим вектор, и без потери общности наших рассуждений, рассмотрим вектор заданный на плоскости. Как известно из курса ещё школьной геометрии, любой вектор можно задать на плоскости с помощью двух неколлинеарных векторов

$vec{a} = a^1 vec{e}_1 + a^2 vec{e}_2.quad (1)$

Здесь $a^i,, i = overline{1,2}$ — коэффициенты разложения, (под верхним индексом следует понимать именно номер компоненты, а не возвдение в степень), называемые контрвариантные координаты вектора vec{a} . Геометрически это можно изобразить так, как показано на рисунке ниже. Векторы $vec{e}_1, vec{e}_2$ называют базисными, угол между ними, при условии , может быть произвольным, произвольна так же ненулевая длина базисных векторов. Указанный базис задает косоугольную систему координат на плоскости, с осями (u,v) .

Исходя из чертежа длины отрезков OA_1 и OA_2 равны

$OA_1 = a^1 left|vec{e}_1 right|,, OA_2 = a^2 left|vec{e}_2 right|quad (2)$

Однако, это не единственный способ определить вектор vec{a} в данной системе координат. Его можно так же задать ортогональными проекциями на оси (u, v) . Нетрудно видеть, что эти проекции равны

$&OB_1 = OA_1 + OA_2cosvarphi = a^1 left|vec{e}_1 right| + a^2 left|vec{e}_2 right| cosvarphiquad (3) \ &OB_2 = OA_1cosvarphi + OA_2 = a^1 left|vec{e}_1 right|cosvarphi + a^2 left|vec{e}_2 right|quad (4)$

С другой стороны, выразим длины этих проекций через длины базисных векторов таким образом
$&OB_1 = a_u = frac{vec{a} cdot vec{e}_1}{left|vec{e}_1 right|} = frac{a_1}{left|vec{e}_1 right|} quad (5) \ &OB_2 = a_v = frac{vec{a} cdot vec{e}_2}{left|vec{e}_2 right|} = frac{a_2}{left|vec{e}_2 right|}quad (6)$

где $a_1 = vec{a} cdot vec{e}_1$ и $a_2 = vec{a} cdot vec{e}_2$ — ковариантные координаты вектора vec{a} .

Сравниваем (3), (5) и (4), (6)

$&frac{a_1}{ left|vec{e}_1 right|} = a^1 left|vec{e}_1 right| + a^2 left|vec{e}_2 right| cosvarphi quad (7) \ &frac{a_2}{ left|vec{e}_2 right|} = a^1 left|vec{e}_1 right|cosvarphi + a^2 left|vec{e}_2 right| quad (8)$

Умножим (7) на $left|vec{e}_1 right|$ , а (8)
на $left|vec{e}_2 right|$ и преобразуем их

$&a_1 = a^1(vec{e}_1 cdot vec{e}_1) + a^2 (vec{e}_1 cdot vec{e}_2) quad (9) \ &a_2 = a^1(vec{e}_1 cdot vec{e}_2) + a^2 (vec{e}_2 cdot vec{e}_2) quad (10)$

Введем матрицу

$mathbf{g} = begin{bmatrix} vec{e}_1 cdot vec{e}_1 && vec{e}_1 cdot vec{e}_2 \ vec{e}_1 cdot vec{e}_2 && vec{e}_2 cdot vec{e}_2 end{bmatrix} quad (11)$

тогда (9) и (10) можно выразить следующим соотношением

$a_i = sum_{j=1}^{2} g_{ij} a^j,, i=1,2 quad (12)$

Выражение (12) дает связь между ковариантными и контрaвариантными координатами вектора, определяемую лишь видом матрицы , зависящей от длин взаимного расположения базисных векторов. Пока никак не будем интерпретировать полученный результат, а просто запомним его.

Набор контравариантных и ковариантных компонент, по сути, задают в выбранном базисе один и тот же вектор. При использовании контравариантных координат этот вектор задается матрицей-столбцом

$mathbf{a} = begin{bmatrix} a^1 \ vdots \ a^n end{bmatrix}$

а в ковариантной форме — матрицей-строкой

$mathbf{a} = begin{bmatrix} a_1 && cdots && a_n end{bmatrix}$

2. Скалярное произведение векторов

Перейдем к пространству более высокой размерности и рассмотрим два вектора

$label{eq:3d-vectors} vec{a} = a^1 vec{e}_1 + a^2 vec{e}_2 + a^3 vec{e}_3,, vec{b} = b^1 vec{e}_1 + b^2 vec{e}_2 + b^3 vec{e}_3$

где базисные векторы $vec{e}_1,vec{e}_2, vec{e}_3$ , как и выше, ненулевые
некомпланарные векторы. Перемножим векторы скалярно.

$vec{a} cdot vec{b} = left(a^1 vec{e}_1 + a^2 vec{e}_2 + a^3 vec{e}_3right) cdot left(b^1 vec{e}_1 + b^2 vec{e}_2 + b^3 vec{e}_3right)$

В последнем выражении аккуратно раскроем скобки

$vec{a} cdot vec{b} = &a^1 b^1 (vec{e}_1 cdot vec{e}_1 ) + a^2 b^1 (vec{e}_1 cdot vec{e}_2 ) + a^3 b^1 (vec{e}_1 cdot vec{e}_3 ) + \ &a^1 b^2 (vec{e}_1 cdot vec{e}_2 ) + a^2 b^2 (vec{e}_2 cdot vec{e}_2 ) + a^3 b^2 (vec{e}_2 cdot vec{e}_3 ) + \ &a^1 b^3 (vec{e}_1 cdot vec{e}_3 ) + a^2 b^3 (vec{e}_2 cdot vec{e}_3 ) + a^3 b^3 (vec{e}_3 cdot vec{e}_3 )$

и снова введем матрицу

$mathbf{g} = begin{bmatrix} vec{e}_1 cdot vec{e}_1 && vec{e}_1 cdot vec{e}_2 && vec{e}_1 cdot vec{e}_3 \ vec{e}_1 cdot vec{e}_2 && vec{e}_2 cdot vec{e}_2 && vec{e}_2 cdot vec{e}_3 \ vec{e}_1 cdot vec{e}_3 && vec{e}_2 cdot vec{e}_3 && vec{e}_3 cdot vec{e}_3 end{bmatrix} quad (14)$

и тогда скалярное произведение можно свернуть весьма компактным образом

$vec{a} cdot vec{b} = sum_{i=1}^3 left(sum_{j=1}^3 g_{ij} a^jright) b^i quad (15)$

Первое, что можно заметить, при уменьшении числа измерений пространства мы перейдем от (14) к (11) а выражение
(15) будет работать и давать склярное произведение векторов, но уже на плоскости. То есть мы получили некую обобщающую форму записи операции скалярного умножения, не зависящую ни от размерности пространства, ни от рассматриваемого базиса, все свойства которого обраны в матрице . Внимательно взглянув на (15) мы поймем ещё одну вещь

$a_i = sum_{j=1}^3 g_{ij} a^j,, i=1,2,3 quad (16)$

что есть ничто иное как ковариантные координаты вектора vec{a} . То есть, (15) можно переписать

$vec{a} cdot vec{b} = sum_{i=1}^3 a_i b^i quad (17)$

Но и это не предел упрощения

3. Правило Эйнштейна

Хитный и проницательный Альберт Эйнштейн придумал правило суммирования, в выражениях подобных (17), избавляющее математика от надоедливой и избыточной sum . В выражениях (16) и (17) можно опустить знак суммы, подразумевая суммирование по повторяющемуся индексу, который называют «немым». То есть, (16) переписываем так

$a_i = g_{ij}, a^j,, i=1,2,3 quad (18)$

здесь j — индекс, по которому происходит суммирование. По правилу, этот индекс должен чередовать свое положение — если у первого множителя он внизу, то у второго должен быть вверху и наоборот. Выражение (17) будет выглядеть так

$vec{a} cdot vec{b} = a_i, b^i quad (19)$

Ну а (15) придет к виду

$vec{a} cdot vec{b} = g_{ij}, a^j, b^i quad (20)$

А теперь мы посмотрим, для чего надо было городить такой огород.

4. Анализ на простых примерах

Допустим, что наш базис — декартов, то есть ортонормированый. Тогда, матрица становится единичной

$mathbf{g} = begin{bmatrix} 1 && 0 && 0 \ 0 && 1 && 0 \ 0 && 0 && 1 end{bmatrix}$

Пусть вектор vec{a} задан в таком базисе. Квадрат длины вектора, как известно, это скалярное произведение этого вектора самого на себя, то есть

$|vec{a}|^2 = vec{a} cdot vec{a} = g_{ij}, a^j, a^i = &left(g_{11} a^1 + g_{12} a^2 + g_{13} a^3right) a^1 + \ & + left(g_{21} a^1 + g_{22} a^2 + g_{23} a^3right) a^2 + \ & + left(g_{31} a^1 + g_{32} a^2 + g_{33} a^3right) a^3 = \ & = (a^1)^2 + (a^2)^2 + (a^3)^2$

И мы получили… квадрат длины вектора, заданного в прямоугольной системе координат!

Ещё пример, дабы не загроможнать который, будем работать в двух измерениях. Пусть система координат подобна той, что изображена на рисунке из параграфа 1, и в ней задан вектор vec{b} своими контравариантными rоординатами. Тогда

$mathbf{g} = begin{bmatrix} 1 && cosvarphi \ cosvarphi && 1 end{bmatrix}$

где varphi — угол между векторами базиса. Вычислим длину вектора vec{b}

$|vec{b}|^2 = vec{b} cdot vec{b} = g_{ij}, b^j, b^i = &left(g_{11} b^1 + g_{12} b^2right) b^1 + left(g_{21} b^1 + g_{22} b^2right) b^2 = \ & = (b^1)^2 + b^2, b^1 cosvarphi + b^1, b^2 cosvarphi + (b^2)^2 = \ & = (b^1)^2 + (b^2)^2 + 2, b^1, b^2 cosvarphi$

Ровно такой же результат мы получим, если воспользуемся теоремой косинусов и найдем квадрат длины диагонали параллелограмма.

Что получается? Работая в разных системах координат, мы использовали одну единственную формулу (20) для вычисления скалярного произведения. И её вид совершенно не зависит ни от базиса, ни от числе измерений пространства, в котором мы работаем. Базисом определяются лишь конкретные значения компонент матрицы .

Так вот, уравнение (20) выражает скалярное произведение двух векторов в тензорной, то есть независимой от выбранного базиса форме.

Матрица задает так называемый метрический тензор. Её вид
определяет каким образом в выбранных координатах вычисляется расстояние между двумя точками.

Но почему мы называем эту матрицу тензором? Следует понимать, что математическая форма, в данном случае квадратная матрица, содержащая набор компонент, это ещё не тензор. Понятие тензора несколько шире, и прежде чем мы скажем, что такое тензор, мы рассмотрим ещё один вопрос.

5. Преобразование метрического тензора при смене базиса

Перепишем соотношение (20) в матричной форме, так нам будет легче оперировать им

$c = mathbf{a}^{(0)T}, mathbf{g}^{(0)}, mathbf{b}^{(0)} quad (21)$

где c — скалярное произведение векторов. Верхний индекс несет смысл системы координат, в которой заданы векторы и определен метрический тензор. Скажем это система координат СК0. Преобразование вектора к некоторой другой системе
координат СК1 описывается матрицей преобразования $mathbf{A}_{01}$ , то есть

$mathbf{a}^{(0)} = mathbf{A}_{01}, mathbf{a}^{(1)}, quad mathbf{b}^{(0)} = mathbf{A}_{01}, mathbf{b}^{(1)} quad (22)$

Подставим (22) в (21)
$c = left(mathbf{A}_{01}, mathbf{a}^{(1)}right)^T, mathbf{g}^{(0)},mathbf{A}_{01}, mathbf{b}^{(1)} = mathbf{a}^{(1)T}, mathbf{A}_{01}^T mathbf{g}^{(0)},mathbf{A}_{01}, mathbf{b}^{(1)}$

в последнем выражении

$mathbf{A}_{01}^T mathbf{g}^{(0)},mathbf{A}_{01} = mathbf{g}^{(1)}$

метрический тензор, компоненты которого определяются новым базисом. То есть, в новом базисе операция имеет аналогичную форму

$c = mathbf{a}^{(1)T}, mathbf{g}^{(1)}, mathbf{b}^{(1)}$

Тем самым мы показали ещё одно свойство тензора — его компоненты меняются синхронно с компонентами векторов того пространства, в котором определен тензор. То есть теперь мы можем сказать, что тензор — это математический объект, представленный набором компонент и правилом их преобразования при смене базиса.

Теперь, используя правило Эйнштейна, перепишем (22) и (23) в тензорной форме

$a^{i(1)} = alpha_k^i a^{k(0)}, quad b^{i(1)} = alpha_k^i b^{k(0)} quad (24)$

$g_{ij}^{(1)} = alpha_i^l , alpha_j^k , g_{kl}^{(0)} quad (25)$

где — элементы матрицы $mathbf{A}_{01}$ . Проиллюстрируем (25) на трехмерном примере. Пусть матрица преобразования координат имеет вид

$mathbf{A}_{01} = begin{bmatrix} alpha_1^1 &&alpha_2^1 && alpha_3^1 \ alpha_1^2 &&alpha_2^2 && alpha_3^2 \ alpha_1^3 &&alpha_2^3 && alpha_3^3 end{bmatrix}$

Распишем преобразование компонента метрического тензора, выполняя суммирование по немым индексам k и l в (25)

$g_{ij}^{(1)} = & alpha_i^1 , left( alpha_j^1 , g_{11}^{(0)} + alpha_j^2 , g_{21}^{(0)} + alpha_j^3 , g_{31}^{(0)} right) + \ & alpha_i^2 , left( alpha_j^1 , g_{12}^{(0)} + alpha_j^2 , g_{22}^{(0)} + alpha_j^3 , g_{32}^{(0)} right) + \ & alpha_i^3 , left( alpha_j^1 , g_{13}^{(0)} + alpha_j^2 , g_{23}^{(0)} + alpha_j^3 , g_{33}^{(0)} right)$

откуда видно что в (25) выполняется транспонирование матрицы перехода, умножение результата на метрический тензор и
умножение полученной матрицы на матрицу перехода.

Теперь рассмотрим конкретный пример, на плоскости, чтобы не писать излишне громоздких выкладок

Пусть вектор vec{a} задан в двух нормированных базисах: прямоугольном
$(vec{e}_{10}, , vec{e}_{20})$ и косоугольном $(vec{e}_{11}, , vec{e}_{21})$ . Преобразование из косоугольной системы координат в прямоугольную выражается матрицей

$mathbf{A}_{01} = begin{bmatrix} cosvarphi && sinvarphi \ sinvarphi && cosvarphi end{bmatrix}$

обратное преобразование

$mathbf{A}_{10} = mathbf{A}_{01}^{-1} = begin{bmatrix} cfrac{cosvarphi}{cos 2 varphi} && -cfrac{sinvarphi}{cos 2 varphi} \ -cfrac{sinvarphi}{cos 2 varphi} && cfrac{cosvarphi}{cos 2 varphi} end{bmatrix}$

Пусть также, в прямоугольных координатах наш вектор имеет компоненты

$mathbf{a}^{(0)} = begin{bmatrix} 3 \ 4 end{bmatrix}$

и совсем нетрудно увидеть, что длина его . Метрический тензор в ортонормированном базисе представляется единичной матрицей

$mathbf{g}^{(0)} = begin{bmatrix} 1 && 0 \ 0 && 1 end{bmatrix}$

значит

$|vec{a}|^2 = g_{ij}^{(0)} , a^{j(0)} , a^{i(0)} & = left( g_{11}^{(0)} , a^{1(0)} + g_{12}^{(0)} , a^{2(0)} right) a^{1(0)} + left( g_{21}^{(0)} , a^{1(0)} + g_{22}^{(0)} , a^{2(0)} right) a^{2(0)} \ & = 3 cdot 3 + 4 cdot 4 = 9 + 16 = 25.$

Зададим угол наклона осей $varphi = frac{pi}{6}$ и вычислим контравариантные компоненты вектора в косоугольных осях

$&a^{1(1)} = tilde{alpha}_1^1 , a^{1(0)} + tilde{alpha}_2^1 , a^{2(0)} = 3sqrt{3} - 4 \ &a^{2(1)} = tilde{alpha}_1^2 , a^{1(0)} + tilde{alpha}_2^2 , a^{2(0)} = -3 + 4sqrt{3}$

Вместе с вектором необходимо преобразовать и метрический тензор

$&g_{11}^{(1)} = alpha_1^1 , left( alpha_1^1 , g_{11}^{(0)} + alpha_1^2 , g_{21}^{(0)} right) + alpha_1^2 , left( alpha_1^1 , g_{12}^{(0)} + alpha_1^2 , g_{22}^{(0)} right) = frac{sqrt 3}{2} cdot frac{sqrt 3}{2} + frac{1}{2} cdot frac{1}{2} = 1 \ &g_{12}^{(1)} = alpha_1^1 , left( alpha_2^1 , g_{11}^{(0)} + alpha_2^2 , g_{21}^{(0)} right) + alpha_1^2 , left( alpha_2^1 , g_{12}^{(0)} + alpha_2^2 , g_{22}^{(0)} right) =frac{sqrt 3}{2} cdot frac{1}{2} + frac{1}{2} cdot frac{sqrt 3}{2} = frac{sqrt 3}{2} \ &g_{21}^{(1)} = alpha_2^1 , left( alpha_1^1 , g_{11}^{(0)} + alpha_1^2 , g_{21}^{(0)} right) + alpha_2^2 , left( alpha_1^1 , g_{12}^{(0)} + alpha_1^2 , g_{22}^{(0)} right) = frac{1}{2} cdot frac{sqrt 3}{2} + frac{sqrt 3}{2} cdot frac{1}{2} = frac{sqrt 3}{2} \ &g_{22}^{(1)} = alpha_2^1 , left( alpha_2^1 , g_{11}^{(0)} + alpha_2^2 , g_{21}^{(0)} right) + alpha_2^2 , left( alpha_2^1 , g_{12}^{(0)} + alpha_2^2 , g_{22}^{(0)} right) = frac{1}{2} cdot frac{1}{2} + frac{sqrt 3}{2} cdot frac{sqrt 3}{2} = 1$

Ну а теперь вычислим длину вектора в новом базисе

$|vec{a}|^2 = g_{ij}^{(1)} , a^{j(1)} , a^{i(1)} & = left( g_{11}^{(1)} , a^{1(1)} + g_{12}^{(1)} , a^{2(1)} right) a^{1(1)} + left( g_{21}^{(1)} , a^{1(1)} + g_{22}^{(1)} , a^{2(1)} right) a^{2(1)} = \ & = left( 3sqrt 3 - 4 - 3frac{sqrt 3}{2} + 6 right) left(3sqrt 3 - 4 right) + \ & + left( frac{9}{2} - 2sqrt 3 - 3 + 4sqrt 3 right) left(-3 + 4sqrt 3right) = \ & = frac{27}{2} + 6sqrt 3 - 6sqrt 3 - 8 - frac{9}{2} - 6sqrt 3 + 6sqrt 3 + 24 = 9 + 16 = 25$

то есть

и скалярное произведение и длина вектора инвариантны, то есть неизменны при преобразовании координат, а так и должно быть. При этом, мы использовали по сути одно и то же соотношение (20) для работы в разных базисах, предварительно преобразовав метрический тензор в соответствии с правилом преобразования векторов в рассматриваемых пространствах
(25).

Заключение и выводы

Что мы увидели в предыдущем параграфе? Если свойства пространства, в котором заданы векторы известны, то для нас не составляет труда выполнить, строго формальным образом, действия над векторами, используя соотношения, вид которых от формы пространства независим. Причем соотношения (20), (24) и (25) дают нам и алгоритм вычисления и способ преобразования компонент выражений, используемых алгоритмом. В этом — мощь и сила тензорного подхода.

Многие физические теории, например ОТО, оперируют искривленным пространством-временем, и там другой подход просто неприемлем. В искривленном пространстве-времени метрический тензор задан локально, в каждой его точке, и если попытаться обойтись без тензоров, у нас ничего не выйдет — мы получим громоздкие и неповоротливые уравнения, если получим их вообще.

В прикладных областях науки тензорная запись выражений применима там, где требуется получать уравнения, независимые от используемой системы координат.

Но это ещё не всё. Мы не поговорили о свойствах метрического тензора, не рассмотрели векторное произведение и тензор Леви-Чевиты. Не поговорили о ранге тензоров и операциях с ними, не разобрались до конца с правилами индексации компонент тензоров и о многом другом. Об этом будет написано несколько позднее, а пока — спасибо всем моим читателям за внимание.

Продолжение следует…

Источник

3. Скалярное и векторное умножение тензора на вектор и тензор. Единичный тензор.

4.След, векторный инвариант, определитель тензора. Теорема о представлении кососимметричного тензора .

Содержание

Введение

1. Вектор на плоскости. Контравариантные, ковариантные координаты и связь между ними

2. Скалярное произведение векторов

3. Правило Эйнштейна

4. Анализ на простых примерах

5. Преобразование метрического тензора при смене базиса

Заключение и выводы

Не пропустите также: