Как найти контактную разность потенциалов - Avtoru.top

Наталья Николаевна Пушкина

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Работа выхода

Факт существования твердых тел говорит о том, что существуют силы, которые удерживают, находящиеся в постоянном движении электроны внутри тела. Для того чтобы из тела извлечь электрон, следует затратить работу. Допустим, что твердое тело находится внутри адиабатической оболочки при постоянной температуре T. В результате теплового движения и перераспределения электронов по скоростям внутри тела кинетической энергии некоторых электронов будет достаточно для преодоления сил, которые удерживают их внутри тела. Из-за этого у поверхности тела возникает «газ» из электронов. Некоторые электроны приближаются к поверхности тела и захватываются внутрь тела. В состоянии термодинамического равновесия среднее количество электронов, покидающих тело, равно среднему числу электронов возвращающихся. Этот «электронный газ» не вырожден, его плотность может быть записана в виде распределения Больцмана:

где $n_0$ — концентрация электронов у поверхности тела, C — зависит только от температуры, $A_Ф$ —работа выхода. Работа выхода связана с энергией $mu $ уровня Ферми соотношением:

где $E_0$ — энергия покоящегося электрона вне проводника в вакууме. То есть $A_Ф$ равна работе по перемещению электрона с уровня $mu $ за пределы твердого тела. Для металлов это утверждение буквально, для диэлектриков несколько условно, так как в них на уровне Ферми нет электронов.

Силы, которые удерживают электроны в твёрдых телах, имеют электрическое происхождение. Они вызваны разностью потенциалов между точками вне тела и внутренними точками. Силы, которые стремятся втянуть электроны внутрь тела тем больше, чем больше работа выхода $A_Ф.$ Они действуют в очень тонком слое (порядка молекулярных размеров $dapprox {10}^{-10}м$). Эффективная напряженность электрического поля ($E_{ef}$), которое вызывает появление этих сил порядка:

где работа выхода принята равной нескольким электрон- вольтам. Работу выхода электронов из металла часто выражают в электрон — вольтах. Это внесистемная единица $1эB=1,602cdot {10}^{-19}Дж.$

«Контактные явления, контактная разность потенциалов» 👇

Контактные явления

Если сблизить поверхности двух тел так близко, что слои их электронного газа перекроются, то тела станут обмениваться электронами. Силы, которые увлекают электрон в тело будут больше у того тела у которого работа выхода больше. После того как сблизили тела с их поверхностей начнется переход электронов от вещества с меньшей работой выхода к веществу с большей работой. Как результат первое тело будет заряжаться положительно, второе отрицательно. Возникающее между телами электрическое поле будет препятствовать движению электронов в результате которого, оно появилось. В состоянии равновесия напряженность поля достигает такого значения, что переход электронов прекращается. Поверхности имеют одинаковые по величине, но противоположные по знаку заряды. Между поверхностями устанавливается некоторая разность потенциалов, которая называется контактной.

Появление контактной разности потенциалов было открыто Вольтой в 1797 г. у металлов. Он расположил металлы в ряд, заметил, что если металлы в определенной им последовательности привести в контакт, то при этом каждый предыдущий металл получит более высокий потенциал, чем следующий. Причем, если несколько металлов одинаковой температуры, привести в контакт, то разность потенциалов между крайними металлами не зависит от того, какими промежуточными металлами они разделяются (закон последовательных контактов Вольты). Если крайние металлы замкнуть в кольцо, то ЭДС в кольце будет равна нулю. Иначе был бы нарушен закон сохранения энергии. Данное положение не применяется, если в цепи есть электролиты, и могут течь химические реакции.

Контактная разность потенциалов

Для того чтобы объяснить существование контактной разности потенциалов можно использовать модель свободных электронов. Если T=0K, то все уровни энергии до границы Ферми ($mu $) будет заполнены электронами.

где $n $— концентрация электронов проводимости.

Допустим, что мы привели в контакт два металла (1) и (2) с энергиями Ферми равными соответственно ${mu }_1
[{mu }_1+q_e{varphi }_{i1}=м_2+q_eц_{i2}left(4right).]

Следовательно,

Так как $q_e{varphi }_{i1}$.

Этот результат справедлив и при $Tne 0.$ В формуле (5) считают, что точка 1 лежит внутри металла (1), а точка 2 внутри второго металла. Это отмечено индексом $i$. Разность потенциалов ${varphi }_{i2}-{varphi }_{i1}$ называют внутренней контактной разностью потенциалов. Из формулы (5) следует, что внутренняя контактная разность потенциалов удовлетворяет закону последовательных контактов Вольты. Используя формулу (3), получим:

Допустим, что между металлами есть зазор микроскопической величины. Возьмем внутри зазора точки $1′ и 2’$, которые лежат на расстоянии порядка чуть больше, чем толщина поверхностного слоя от границ соответствующих металлов. Потенциалы во внешних точках обозначим как ${varphi }_{e2} и {varphi }_{e1}$. Их разность называют внешней контактной разностью потенциалов. Величину внешней контактной разности потенциалов определяют как:

где $A_2,A_1$ — работы выхода на границах металлов. Присутствие внешней контактной разности потенциалов означает, что в зазоре между металлами есть электрическое поле.

Внешняя контактная разность потенциалов также подчиняется закону контактов Вольты.

Пример 1

Задание: Оцените, чему равна внутренняя контактная разность потенциалов для меди.

Решение:

В качестве основы для решения задачи используем формулу:

[{varphi }_{i2}-{varphi }_{i1}=frac{h^2}{8m_eq_e}{left(frac{3}{pi }right)}^{frac{2}{3}}left({n_1}^{frac{2}{3}}-{n_2}^{frac{2}{3}}right)left(1.1right),]

где $h=6,63cdot {10}^{-34}Джcdot с,$ $m_e=9,1 cdot {10}^{-31}кг$, $q_e=1,6cdot {10}^{-19}Кл.$ Если на каждый атом приходится один свободный электрон, тогда, получим:

[{varphi }_{i2}-{varphi }_{i1}=-3,66cdot {10}^{-15}n^{frac{2}{3}}sim 1 left(Bright).]

Ответ: Для меди ${varphi }_{i2}-{varphi }_{i1}approx 1 В.$

Пример 2

Задание: Схематично изобразите образование контактной разности потенциалов между двумя металлами и между двумя диэлектриками.

Решение:

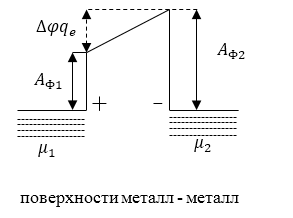
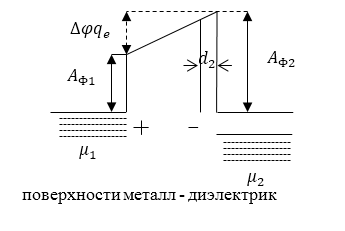
Отличие в образовании контактной разности потенциалов в металлах и диэлектриках состоит том, что электрическое поле не проникает внутрь металлов, но проникает на небольшую глубину внутрь диэлектриков ($d_2-глубина проникновения поля в диэлектрике$). У диэлектрика падение потенциала происходит не только между поверхностями, но и частично в тонком слое внутри диэлектрика около его поверхности. Но, надо сказать, что толщина этого слоя мала в сравнении с расстоянием между поверхностями, поэтому часто им пренебрегают.

Рисунок 1.

Рисунок 2.

Из рис. 1 видно, что разность между энергий верхних точек потенциальных ям равна $A_{Ф2}-A_{Ф1}$. Значит контактная разность потенциалов между поверхностями тел, в случае их равновесия, задана формулой:

[triangle varphi =frac{left|A_{Ф2}-A_{Ф1}right|}{left|q_eright|} left(2.1right).]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Контактная разность потенциалов. Контакт двух металлов. Законы Вольта

Контактными
называется ряд физических явлений,
возникающих в области соприкосновения
разнородных тел. Практический интерес
контактные явления представляют в
случае контакта металлов и полупроводников.

Объясним возникновение
контактной
разности потенциалов,
воспользовавшись представлениями
зонной теории. Рассмотрим контакт двух
металлов с различными работами выхода
А_вых1
и А_вых2.
Зонные энергетические диаграммы обоих
металлов приведены на рис. 2. У этих
металлов также различны уровни Ферми
(уровень Ферми или энергия Ферми (E_F)
– энергия, ниже которой все энергетические
состояния заполнены, а выше – пусты при
абсолютном нуле температуры). Если А_вых1
< А_вых2
(рис. 2), то в металле 1 уровень Ферми
располагается выше, чем в металле 2.
Следовательно, при контакте металлов
электроны с более высоких уровней
металла 1 будут переходить на более
низкие уровни металла 2, что приведет к
тому, что металл 1 зарядится положительно,
а металл 2 — отрицательно.

Одновременно
происходит относительное смещение
энергетических уровней: в металле,
заряжающемся положительно, все уровни
смещаются вниз, а в металле, заряжающемся
отрицательно, — вверх. Этот процесс
будет происходить до тех пор, пока между
соприкасающимися металлами не установится
термодинамическое равновесие, которое,
как доказывается в статистической
физике, характеризуется выравниванием
уровней Ферми в обоих металлах (рис. 3).
Поскольку теперь для соприкасающихся
металлов уровни Ферми совпадают, а
работы выхода А_вых1
и А_вых2
не изменяются, то потенциальная энергия
электронов в точках, лежащих вне металлов
в непосредственной близости от их
поверхности (точки А и В на рис. 3), будет
различной. Следовательно, между точками
А и B
устанавливается разность потенциалов,
которая, как следует из рисунка, равна

Разность потенциалов,
обусловленная различием работ выхода
контактирующих металлов, называется
внешней
контактной разностью потенциалов —
∆φ_внеш
или просто контактной разностью
потенциалов.

Разность уровней
Ферми в контактирующих металлах приводит
к возникновению внутренней
контактной разности потенциалов,
которая равна

Внутренняя
контактная разность потенциалов ∆φ_внут
зависит от температуры Т контакта
металлов (поскольку положение самого
E_F
зависит от Т), обусловливая многие
термоэлектрические явления. Как правило
∆φ_внут
<< ∆φ_внеш.

При приведении в
соприкосновение трёх разнородных
проводников разность потенциалов между
концами разомкнутой цепи после
установления термодинамического
равновесия окажется равной алгебраической
сумме разностей потенциалов во всех
контактах.

Согласно
представлениям электронной теории,
проводимость металлов обусловлена
наличием в них свободных электронов.
Электроны находятся в состоянии
беспорядочного теплового движения,
подобного хаотическому движению молекул
газа. Число свободных электронов n,
заключенных в единице объема (концентрация),
не одинаково у разных металлов. Для
металлов концентрации свободных
электронов имеют порядок 10²⁵-10²⁷
м^-3.

Предположим, что
концентрации свободных электронов в
металлах неодинаковы — n₁
≠ n₂.
Тогда за одно и то же время через контакт
из металла с большей концентрацией
электронов перейдет больше, чем в
обратном направлении (концентрационная
диффузия). В области контакта дополнительно
возникнет разность потенциалов ∆φ_внут.
В области контакта концентрация
электронов будет плавно изменяться от
n₁
до n₂.
Для расчета ∆φ_внут
выделим в области контакта небольшой
объем, имеющий форму цилиндра с
образующими, перпендикулярными границе
раздела металлов (рис. 4), и будем считать,
что у первого металла концентрация
электронов равна n₁
= n,
а у второго она больше, т.е. n₂
= n+dn.

Далее будем
рассматривать свободные электроны как
некоторый электронный газ, удовлетворяющий
основным представлениям
молекулярно-кинетической теории
идеальных газов. Давление p
газа в основании цилиндра 1 при температуре
T
равно:

(3)

где
– постоянная Больцмана.

Давление в основании
цилиндра 2 соответственно будет:

(4)

Разность давлений
вдоль цилиндра равна:

(5)

Под влиянием
разности давлений возникнет поток
электронов через границу раздела
металлов из области большего давления
р₂
в направлении основания 1 (а на рис. 4).
Равновесие наступит, когда сила dF_эл
возникшего электрического поля с
напряженностью E
(рис. 4) станет равной силе давления dp×dS
электронного газа, т.е.

(6)

Если число электронов
в объёме dV=dx×dS
цилиндра равно dN=ndV,
то сила электрического поля, действующая
на них, будет определяться:

Напряжённость E
электрического поля численно равна
градиенту потенциала
,
т.е.

(8)

(7)

(10)

Подставляя E
в формулу (7) и далее в уравнение (6), с
учётом формулы (5) получим:

Разделим переменные

(9)

Проинтегрируем:

(10).

Поскольку
концентрации свободных электронов у
металлов различаются незначительно,
то величина ∆φ_внут
существенно меньше разности потенциалов
∆φ_внеш.
Величина ∆φ_внут
достигает нескольких десятков милливольт,
тогда как ∆φ_внеш
может иметь порядок нескольких вольт.

Полная разность
потенциалов при контакте металлов с
учетом формулы (10) определяется:

(11)

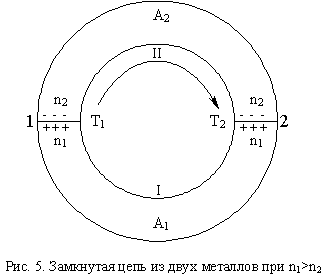
Рассмотрим теперь
замкнутую цепь из двух различных
проводников (рис. 5). Полная разность
потенциалов в этой цепи равна сумме
разностей потенциалов в контактах 1 и
2:

(12)

При указанном на
рис. 3 направлении обхода ∆φ₁₂
= -∆φ₂₁.
Тогда уравнение для всей цепи:

(13)

Если T₁≠T₂,
то и ∆φ ≠ 0.
Алгебраическая сумма всех скачков
потенциалов в замкнутой цепи равна
электродвижущей силе (ЭДС), действующей
в цепи. Следовательно, при T₁
≠ T₂
в цепи (рис. 5) возникает ЭДС, равная в
соответствии с формулами (12) и (13):

(14)

Обозначим

(15)

Следовательно
формула (15) примет вид

(16)

Таким образом ЭДС
в замкнутой цепи из однородных проводников
зависит от разности температур контактов.
Термо-ЭДС
— электродвижущая сила ε,
возникающая в электрической цепи,
состоящей из нескольких разнородных
проводников, контакты между которыми
имеют различные температуры (эффект
Зеебека). Если вдоль проводника существует
градиент температуры, то электроны на
горячем конце приобретают более высокие
энергии и скорости. В полупроводниках,
кроме того, концентрация электронов
растёт с температурой. В результате
возникает поток электронов от горячего
конца к холодному, на холодном конце
накапливается отрицательный заряд, а на горячем
остаётся нескомпенсированный положительный
заряд. Алгебраическая сумма таких
разностей потенциалов в цепи создаёт
одну из составляющих термо-ЭДС, которую
называют объёмной.

Контактная разность
потенциалов может достигать нескольких
вольт. Она зависит от строения проводника
(его объемных электронных свойств) и от
состояния его поверхности. Поэтому
контактную разность потенциалов можно
изменять обработкой поверхностей
(покрытиями, адсорбцией и т. п.).

Анализируя всё
выше написанное, можно сделать выводы,
известные как законы
Вольта:

Контактная разность
потенциалов, возникающая при соединении
двух металлов, зависит только от их
химического состава (т.е. от А_вых
и концентрации n)
и температуры контактов.
В
замкнутой цепи, состоящей из разнородных
металлов, находящихся при одинаковой
температуре (Т₁=Т₂),
контактная разность потенциалов
∆φ
равна нулю (ЭДС и ток в цепи не возникают).
Разность потенциалов
на концах цепи, состоящей из нескольких
последовательно соединенных различных
металлов, не зависит от количества
звеньев цепи и химического состава
промежуточных проводников. Она равна
контактной разности потенциалов лишь
крайних проводников цепи.

В самом деле, для
цепи, показанной на рис. 6:
.

Термоэлектрические
приборы и их практическое применение

Если электрическая
цепь состоит из двух различных проводников,
она называется термоэлементом
или термопарой
(рис. 7).

Термопара является
простейшим термоэлектрическим прибором.
Она представляет собой две проволоки
из разных металлов, концы которых спаяны
или сварены. Для защиты от внешних
воздействий проволоки обычно помещают
в тугоплавкий чехол (керамическую
трубку).

В измерительной
практике получили распространение
термопары, характеристики которых
показаны в таблице 1.

В технике термопары
применяют для контроля и измерения
температуры. Если для термопары известна
постоянная С
и один спай её держать при известной,
постоянной температуре (например, Т₂),
то по возникающей, измеренной вольтметром,
ЭДС можно определить измеряемую
температуру Т₁
(формула 16). Третий закон Вольта утверждает,
что промежуточные проводники не оказывают
существенного влияния на показания
термопар. Это дает возможность применять
их для дистанционного контроля температуры
(в загазованных цехах и т.д.)

Таблица 1

Сравнительная
таблица постоянной термопары и рабочего
диапазона температур для термопар из
различных материалов

Материалы термопары	Постоянная , мкВ/К	Рабочий диапазон температур, º С
Медь-константан (40% Ni + 60% Cu)	41,6	(-200) ÷ (+600)
Железо-константан	52	(-190) ÷ (+800)
Хромель-алюмель	42	(0) ÷ (+1000)
Платина-платина + 10% родия	6,4	(-140) ÷ (+1600)

Для повышения
чувствительности измерительной схемы
термопары можно соединять последовательно
в термобатареи
(рис. 8). ЭДС такой батареи будет равна
сумме ЭДС отдельных термопар.

Для измерения
энергии теплового излучения применяют
термостолбики. Они представляют собой
термобатарею из большого числа термопар,
расположенных так, что излучение может
падать только на четные или нечетные
спаи. Термостолбики обладают очень
высокой чувствительностью, по сравнением
с отдельной термопарой.

Термобатареи
представляют интерес и как генераторы
электрического тока. Они непосредственно
преобразуют тепловую энергию в
электрическую. Однако КПД их низок
(примерно 0,1%), и поэтому на практике они
мало используются. Более высоким КПД
обладают термоэлементы, изготовленные
не из металлов, а из полупроводников
(их КПД имеет величину порядка 6 – 8 %, а
постоянная С
≈ 10^-3
В/К).

Существуют также
термоэлектрические приборы для измерения
токов и напряжений. Они представляют
собой амперметры или вольтметры в
сочетании с термопреобразователем
(термопарой или термобатареей). При
прохождении тока по проводнику
термопреобразователя (рис. 9) в нем
выделяется ленц-джоулево тепло, которое
нагревает один из спаев термопары, и
величину возникшей термо-ЭДС фиксирует
прибор. Тепло, выделяемое переменным
током, практически не зависит от его
частоты, поэтому термоэлектрическими
приборами можно измерять в цепях как
постоянного, так и переменного тока.

Схема установки

В данной работе
опытным путём определяют зависимость
термо-ЭДС от разности температур спаев
термопары, рассчитывают её постоянную
С
и отношение
концентраций свободных электронов.

По указанию
преподавателей работа может выполняться
в двух вариантах.

Упражнение 1.
Измерения термо-ЭДС гальванометром

Соберите установку
в соответствии с рис. 10.

Согласно закону
Ома в замкнутой цепи (рис. 10) ЭДС (в вашем
случае термо-ЭДС) равна:

где R
— сопротивление гальванометра; r
— сопротивление термопары. Гальванометр
подбирают с много большим сопротивлением
(R>>r),
тогда ε=IR,
т.е. показания гальванометра в вольтах
мало отличаются от измеряемой термо-ЭДС.

Соседние файлы в папке физика_1

#
#
#
28.03.2016147.46 Кб3749.doc
#
28.03.2016112.64 Кб255.doc
#
#
#
#
#
#
28.03.2016155.14 Кб256.doc
#
28.03.2016109.57 Кб2260.doc

Источник

Что такое контактная разность потенциалов и от чего она зависит

Между двумя разными металлами при тесном соприкосновении возникает явление, получившее название контактная разность потенциалов. Данное явление связано с особенностями строения вещества. Далее рассмотрим и узнаем о механизме его работы.

История изучения

Контактную разность потенциалов обнаружил и исследовал итальянский физик Алессандро Вольта в 1797 году. Он проводил опыты, соединяя диски из различных металлов стопкой в строго определённом порядке и измеряя возникающее между ними напряжение. Например, в одном из опытов он соединил плоскими сторонами диски из следующих материалов в указанном порядке: Al, Zn, Sn, Pb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd. В этом ряду у каждого последующего металла потенциал был ниже, чем у предыдущего. Ученый обобщил результаты своих опытов и сформулировал законы, названные его именем.

Электроны в твёрдом теле

Любое твёрдое тело состоит из атомов. В каждом из них вокруг ядра вращаются электроны. Иногда они покидают атом и двигаются случайным образом вне его. После того как атом теряет электрон, он становится ионом, приобретая положительный заряд. В результате ион начинает притягивать электроны, которые возвращаются на свои орбиты.

Эти процессы происходят не только внутри твёрдого тела, но и в некоторых случаях за его пределами. Следовательно, можно представить, что очень близко от его границ существует электронное облако. Одни частицы пополняют его, другие — возвращаются внутрь тела.

Если твёрдые тела соприкоснутся, то электронные облака у их поверхностей перемешаются. В этом случае часть электронов будет покидать то или другое тело, а некоторые из них переместятся внутрь одного из них. Однако этот процесс не будет проходить одинаково в обоих случаях.

Контакт поверхностей

Чтобы электрон вышел за пределы твёрдого тела, он должен выполнить определённую работу. Важно отметить, что в различных случаях её величина может отличаться. В том теле, для выхода из которого электрону придется проделать большую работу, количество заряженных частиц будет выше. Эта неравномерность приведёт к тому, что на границе соприкосновения образуется контактная разность электрических потенциалов. Одно из тел станет заряженным положительно, а другое — отрицательно.

Ещё один фактор, который влияет на неравномерность распределения, это плотность облака электронов. Частицы из более плотного постепенно диффузируют в относительно разряженное состояние.

Если неравномерность распределения частиц усиливается, возникающее электрическое поле увеличивается. Оно стабилизируется лишь в том случае, когда начнет препятствовать увеличению заряда. Следовательно, можно сказать, что контактная разность электрических потенциалов — это результат работы, проделанной электронами.

Величина потенциалов не зависит от площади соприкосновения или геометрической формы тел. Существенную роль играет химический состав металла и его температура. При её росте увеличивается концентрация собственных носителей заряда, что приводит к уменьшению контактной разности потенциалов.

Чтобы покинуть атом, электрон должен выполнить определённую работу. Допустим, эта величина равна A для одного материала и B для другого. Для определённости предположим, что A > B. В таком случае поверхность первого проводника постепенно заряжается положительно, а второго — отрицательно.

При этом разность потенциалов U между ними будет расти. Однако по мере ее увеличения будет наблюдаться и больше переходов электронов между материалами. Когда разность потенциалов достигнет предельной величины, переход электронов в обе стороны станет равновероятным. Величину контактной разности потенциалов можно найти по формуле:

Величину U в рассматриваемом случае называют внешней контактной разностью потенциалов. На практике она в большинстве случаев колеблется от десятых долей до нескольких вольт. Речь идёт о разности потенциалов между точками, которые находятся очень близко к поверхности, но при этом вне её. Если рассматривать аналогичную величину между точками рядом с границей поверхности, но за ней для каждого материала, то речь будет идти о внутренней контактной разности потенциалов.

С одной контактирующей поверхности на другую может перейти не более двух процентов свободных электронов. Из-за этого контактное электрополе локализуется исключительно в зоне соприкосновения и практически не захватывает внутренние области контактирующих тел.

Видео по теме

Источник

В предыдущих разделах мы рассмотрели свободную эмиссию электронов
из катода, когда внешнего поля между анодом и катодом не было задано.
Но если внешнюю цепь анод–катод замкнуть проводником, то в пространстве
анод–катод внутри диода создастся некоторая разность потенциалов,
природа которой — контактная разность потенциалов — непосредственно
связана с величиной работы выхода электронов из металлов и током эмиссии.

Суть этого явления заключается в следующем. Рассмотрим проводники
из различных металлов, например, вольфрама (катод 1) и никеля (анод
2), с работами выхода 4,55 и 4,5 эВ соответственно (рис. 5).

На рис. 5, а потенциальные ямы металлов изображены относительно нулевого
уровня потенциала А. Нас будет интересовать вопрос: что произойдет
при соединении проводников, показанном на рис. 5, б? Оказывается,
как и в случае обычного молекулярного газа, когда при соединении двух
сосудов с различной плотностью газа последняя будет выравниваться
за счет процессов диффузии, в случае электронного газа тоже происходит
«выравнивание» плотностей электронов. Выравнивание происходит
до тех пор, пока уровни энергии Ферми обоих металлов не станут равными,
т. е. пока не установится единый химический потенциал электронного
газа в системе из двух металлов. При этом часть электронов из металла
с меньшей работой выхода перетечет в другой металл, и первый зарядится
положительно относительно другого. Разность уровней Ферми определит
так называемую внутреннюю контактную разность потенциалов
$$
U’_{C}=-frac{varphi_{f_1}-varphi_{f_2}}{e}
$$
(между концами 1 – 2), а разность работ выхода — внешнюю (между
концами 1′ – 2′)
$$
U_{C}=-frac{varphi_{a_1}-varphi_{a_2}}{e}.
$$

Можно показать, что величина внешней контактной разности потенциалов
(или просто контактной разницы потенциалов) $U_{C}$ не изменяется,
если в промежуток между концами 1 и 2 вставить любые другие металлы.
Величина $U_{C}$ определится только разностью работ выхода металлов,
«открытых» в промежуток между ними (концов 1′ – 2′). Поэтому
при замыкании внешней электрической цепи анод – катод диода величина
внешней контактной разности потенциалов оказывается приложенной к
промежутку катод–анод внутри диода и создает в нем напряженность
поля, влияющую на движение термоэлектронов.

Назад к теме Модель потенциальной ямы (модель Шоттки) или далее Режимы работы диода

Источник

Работа выхода

Контактные явления

Контактная разность потенциалов

Контактная разность потенциалов. Контакт двух металлов. Законы Вольта

Что такое контактная разность потенциалов и от чего она зависит

История изучения

Электроны в твёрдом теле

Контакт поверхностей

Видео по теме

Не пропустите также: