-
Характеристика кинетических констант
В
уравнении Михаэлиса есть два кинетических
параметра, имеющих важное значение для
характеристики любого фермента. Это
константа Михаэлиса и максимальная
скорость реакции. Константа Михаэлиса
определяется соотношением констант
(k—1+k+2/k+1),
а величина Vmax,
называемая максимальной скоростью, ‒
произведением k+2
[E]0.
Константа
Михаэлиса численно равна концентрации
субстрата, при которой начальная скорость
ферментативной реакции равна половине
максимальной. Высокое сродство фермента
к субстрату характеризуется низкой
величиной Кm
и наоборот, низкое сродство – высокой
величиной Км.
Величина
Vmax
не является фундаментальной характеристикой
фермента, поскольку зависит от его
концентрации. Если концентрация фермента
известна, то целесообразно ввести
величину kcat
– каталитическую константу (или число
оборотов фермента), определяемую
выражением Vmax/[E]0.
Для механизма Михаэлиса kcat
идентична
k+2,
однако в общем случае лучше пользоваться
менее определенным обозначением, а
именно kcat.
Константу
kкат
называют
еще «числом
оборотов»
поскольку она соответствует числу
молекул субстрата, превращаемых в
продукт одной молекулой фермента за 1
с. Отношение констант kcat/Км
называют
константой специфичности фермента.
-
Методы определения Км и Vmax
Константу
Михаэлиса можно определить из графика
Михаэлиса (рис.1.1), найдя графическим
способом максимальную скорость и
соответствующую величину концентрации
субстрата, при которой скорость
ферментативной реакции будет вдвое
меньше Vmax.
Эта величина [S]
и будет Км.
Таким способом можно определить только
приблизительную величину константы
Михаэлиса из-за трудности точного
графического определения Vmax.
Более
удобными являются методы, в которых
осуществлена линеаризация уравнения
Михаэлиса-Ментен, т. е. гиперболическая
зависимость v
от [S]
переведена в линейную.
Для
того чтобы построить такой график,
необходимо определить в одинаковых
условиях при различных концентрациях
субстрата и [E]=
const
начальные скорости ферментативной
реакции.
Метод
Лайнуивера-Берка.
Один из способов линеаризации уравнения
Михаэлиса-Ментен предложили Лайнуивер
и Берк (Lineweaver
H.,
Burk
D.)).
Это так называемый метод двойных обратных
величин. Для линеаризации необходимо
взять обратные величины от левой и
правой частей уравнения (), в результате
чего оно преобразуется в уравнение вида
согласно
которому между величинами, обратными
начальной скорости (1/v,
v-1)
и концентрации субстрата (1/[S],
[S]-1)
соблюдается линейная зависимость, если
механизм реакции подчиняется изложенным
выше представлениям (рис.1.2).
Рис.
1.2. График зависимости 1/v
от 1/[S]
(график Лайнуивера-Берка)
Экспериментальная
прямая пересекает ось абсцисс в точке
(-1/[S]
= 1/Км),
а ось ординат – в точке (1/v
= 1/Vмах).
Тангенс угла наклона равен Км/Vмах.
Этим широко пользуются для определения
параметров Км
и Vмах,
характеризующих связывающую и
каталитическую функции ферментов.
Метод
Хайнса-Вульфа.
В этом случае преобразуется уравнение
Лайнуивера-Берка путем умножения правой
и левой частей на концентрацию субстрата.
Графическая
зависимость приведена на рис.1.3.
Рис.
1.3. График зависимости [S]/v
от [S]
(график Хайнса-Вульфа)
Это
прямая с наклоном 1/Vmax,
отсекающая на осях [S]/v
и [S]
отрезки Км/
Vmax
и – Км соответственно.
Метод
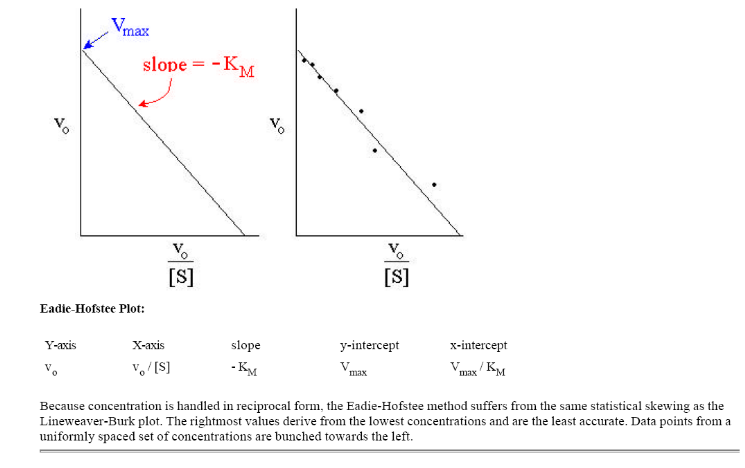
Иди-Хофсти.
При одном из таких графических
преобразований в так называемом графике
Иди-Хофсти (pиc.2.3.5)
строят график зависимости v от v/[S].
В этом случае точка пересечения прямой,
полученной путем наилучшей линейной
аппроксимации экспериментальных точек,
с осью ординат соответствует Vmax,
а тангенс угла наклона равен – Km.
Данный способ линеаризации приведен
на рис. 1.4.
Рис.
1.4. График зависимости v
от v/[S]
(график Эди-Хофсти)
Метод
Эйзенталя и Корниш-Боудена.
Много позднее Эйзенталь и Корниш-Боуден
предложили иной метод графического
представления результатов исследования
кинетики ферментативных реакций – так
называемый прямой линейный график.
Уравнение Михаэлиса-Ментен они
преобразовали в виде зависимости Vmax
от Км:
КМ
= v
+ v/[S]
VMA
Для
любой пары значений [S]
и v
можно построить зависимость Vmax
от Км.
Она представляет прямую с наклоном,
равным v/[S],
и отрезками, отсекаемыми на осях Км
и Vmax,
соответственно равными – [S]
v.
Если провести прямые для нескольких
пар значений [S]
и v,
то эти прямые пересекутся в одной точке,
координаты которой дадут единственные
значения Vmax
от Км,
удовлетворяющие всем парам значений
[S]
и v
(рис.1.5).
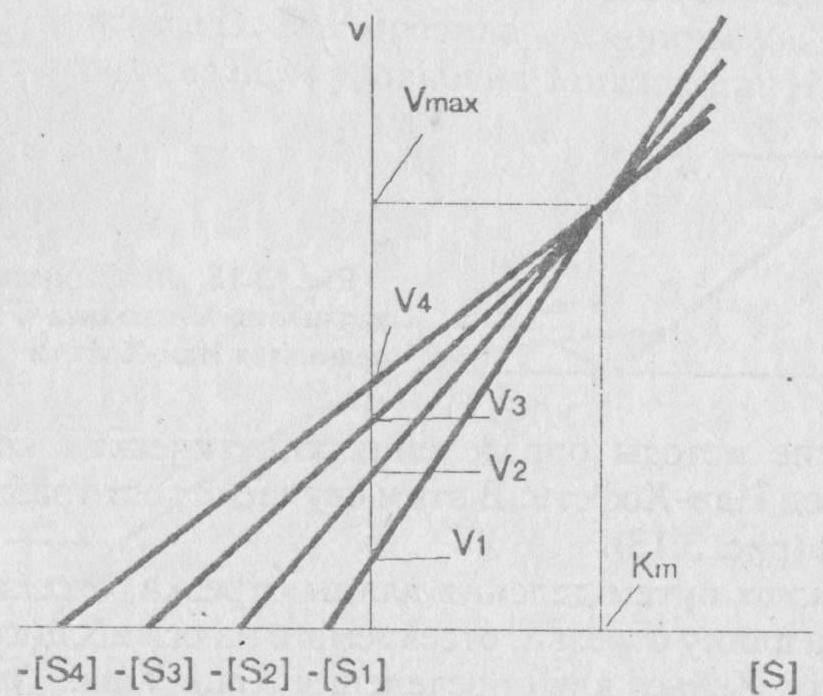
Рис.1.5.
Определение кинетических констант –
Км и Vmax
по методу Эйзенталя и Корниш-Боудена
Преимущества
такого графика очевидно: для его
построения не требуется никаких расчетов,
он позволяет очень просто выявить
ошибочные данные (такие прямые будут
выпадать из основной совокупности
прямых).
Уравнение
Михаэлиса лежит в основе всех кинетических
исследований ферментативных реакций,
так как оно позволяет рассчитать
количественные характеристики ферментов
и проводить анализ их ингибирования.
Величины Кm
и Vmax
являются важнейшими характеристиками
ферментов и их можно определить, используя
линеаризованные формы уравнения
Михаэлиса-Ментен.
Графические
методы для определения Vmax
и Кm
не являются оптимальными. В настоящее
время данные ферментативной кинетики
обрабатывают быстрее и более объективно
с помощью компьютерных программ.
Соседние файлы в папке Биоинж_энзимология
- #
- #
25.05.201556.97 Кб43Задачи_энзимология.xlsx
- #
- #
Методы определения Км и Vmax
Константу Михаэлиса можно определить из графика Михаэлиса (рис.2.2.1), найдя графическим способом максимальную скорость и соответствующую величину концентрации субстрата, при которой скорость ферментативной реакции будет вдвое меньше Vmax. Эта величина [S] и будет Км. Таким способом можно определить только приблизительную величину константы Михаэлиса из-за трудности точного графического определения Vmax.
Более удобными являются методы, в которых осуществлена линеаризация уравнения Михаэлиса-Ментен, т. е. гиперболическая зависимость v от [S] переведена в линейную.
Для того чтобы построить такой график, необходимо определить в одинаковых условиях при различных концентрациях субстрата и [E]= const начальные скорости ферментативной реакции.
Метод Лайнуивера-Берка. Один из способов линеаризации уравнения Михаэлиса-Ментен предложили Лайнуивер и Берк (Lineweaver H., Burk D.). Это так называемый метод двойных обратных величин. Для линеаризации необходимо взять обратные величины от левой и правой частей уравнения (3), в результате чего оно преобразуется в уравнение вида,
согласно которому между величинами, обратными начальной скорости (1/v, v -1 ) и концентрации субстрата (1/[S], [S] -1 ) соблюдается линейная зависимость, если механизм реакции подчиняется изложенным выше представлениям (рис.2.2.3).
Рис. 2.2.3. График зависимости 1/v от 1/[S] (график Лайнуивера-Берка)
Экспериментальная прямая пересекает ось абсцисс в точке (-1/[S] = 1/Км), а ось ординат – в точке (1/v = 1/Vмах). Тангенс угла наклона равен Км/Vмах. Этим широко пользуются для определения параметров Км и Vмах, характеризующих связывающую и каталитическую функции ферментов.
Метод Хайнса-Вульфа. В этом случае преобразуется уравнение Лайнуивера-Берка путем умножения правой и левой частей на концентрацию субстрата.
Графическая зависимость приведена на рис.2.2.4.
Рис. 2.2.4. График зависимости [S]/v от [S] (график Хайнса-Вульфа)
Это прямая с наклоном 1/Vmax, отсекающая на осях [S]/v и [S] отрезки Км/ Vmax и – Км соответственно.
Метод Иди-Хофсти. При одном из таких графических преобразований в так называемом графике Иди-Хофсти(pиc.2.2.5) строят график зависимости v от v/[S]. В этом случае точка пересечения прямой, полученной путем наилучшей линейной аппроксимации экспериментальных точек, с осью ординат соответствует Vmax, а тангенс угла наклона равен – Km. Данный способ линеаризации приведен на рис. 2.2.5.
Рис. 2.2.5. График зависимости v от v/[S] (график Эди-Хофсти)
Метод Эйзенталя и Корниш-Боудена. Много позднее Эйзенталь и Корниш-Боуден предложили иной метод графического представления результатов исследования кинетики ферментативных реакций – так называемый прямой линейный график. Уравнение Михаэлиса-Ментен они преобразовали в виде зависимости Vmax от Км:
Для любой пары значений [S] и v можно построить зависимость Vmax от Км. Она представляет прямую с наклоном, равным v/[S], и отрезками, отсекаемыми на осях Км и Vmax, соответственно равными -[S] v. Если провести прямые для нескольких пар значений [S] и v, то эти прямые пересекутся в одной точке, координаты которой дадут единственные значения Vmax от Км, удовлетворяющие всем парам значений [S] и v (рис.2.2.6).
Преимущества такого графика очевидно: для его построения не требуется никаких расчетов, он позволяет очень просто выявить ошибочные данные (иакие прямые будут выпадать из основной совокупности прямых).
Уравнение Михаэлиса лежит в основе всех кинетических исследований ферментативных реакций, так как оно позволяет рассчитать количественные характеристики ферментов и проводить анализ их ингибирования. Величины Кm и Vmax являются важнейшими характеристиками ферментов и их можно определить, используя линеаризованные формы уравнения Михаэлиса-Ментен.
В заключении необходимо отметить, что графические методы для определения V и Кm не являются оптимальными. В настоящее время данные ферментативной кинетики обрабатывают быстрее и более объективно с помощью компьютерных программ.
Процессы, приводящие к денатурации фермента, могут иметь различную физико-химическую природу. Конформация белковой молекулы в растворе зависит от двух показателей – величины рН и температуры. Повышение температуры приводит к нарушению системы слабых связей, стабилизирующих белковую молекулу. Длительное воздействие повышенной температуры приводит к необратимым изменениям структуры фермента, сопровождающимся потерей активности (тепловая денатурация).
Каждый фермент характеризуется соответствующим зарядом, создаваемым ионогенными группами аминокислотных остатков. При очень низких или высоких значениях рН изменение степени ионизации функциональных групп может приводить к необратимым нарушениям нативной конформации молекулы фермента с разрушением структуры активного центра.
Конформационные изменения в белковой молекулу сопровождаются изменениями спектров поглощения и флуоресценции ароматических аминокислот – тирозина и триптофана в ультрафиолетовой области спектра (
290 нм), что позволяет отслеживать изменения в структуре фермента. Обратимые конформационные, вызванные изменением температуры или концентрацией протонов водорода, осуществляются в течение 10 -4 – 10 -1 с, необратимые денатурационные изменения в зависимости от условий – в течение 1-10 3 мин. Более подробный анализ кинетики денатурации ферментов рассмотрен в Теме 5 учебного пособия по самостоятельной работе.
Лекция_методы определения константы михаэлиса и максимальной скорости процесса
Существует несколько методов определения параметров уравнения Михаэлиса-Ментен (константы Михаэлиса и максимальной скорости реакции) для односубстратной реакции. Наиболее распространенный из них – линеаризация уравнения Михаэлиса-Ментен. Полный анализ включает определение не только Vmax и KM, но и KS, k1, k-1, k2.
Из кривой, построенной на основе исходного уравнения Михаэлиса-Ментен, можно определить графическим методом значения констант Vmax и KM, но это неудобно, так как невозможно провести асимптоту к гиперболе с хорошей точностью.
Первый способ линеаризации был описан Холдейном и Штерном в их учебнике по энзимологии. Для осуществления такого преобразования уравнение Михаэлиса-Ментен представляют в двойных обратных координатах, то есть, единицу делят на V0 и переворачивают дробь в правой части уравнения:
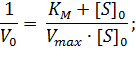 |
(1) |
Преобразовав уравнение (1), получаем один из часто применяемых способов линеаризации – уравнение Лайнуивера-Берка:
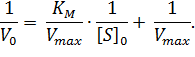 |
(2) |
При построении зависимости в двойных обратных координатах, 1/V0 от 1/[S]0, как показано на рисунке 1, получаем прямую. Из уравнения линейной регрессии можно определить интересующие константы.
Отсекаемый отрезок на оси ординат дает обратную максимальную скорость, а на оси абсцисс – обратную константу Михаэлиса с противоположным знаком. Или же определяют непосредственно из уравнения прямой обратную максимальную скорость, а потом константу Михаэлиса из тангенса угла наклона прямой (рисунок 1).
Точность определения кинетических параметров таким способом считается невысокой. Чем меньше концентрация субстрата, тем выше оказывается ошибка определения обратной скорости.
Домножив обе части уравнения (2) на начальную концентрацию субстрата [S]0, получаем уравнение Хейнса:
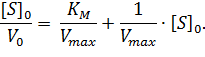 |
(3) |
Построив зависимость [S]0/V0 от [S]0, как показано на рисунке 2, получим прямую, из уравнения линейной регрессии которой можно определить параметры Vmax и KM.
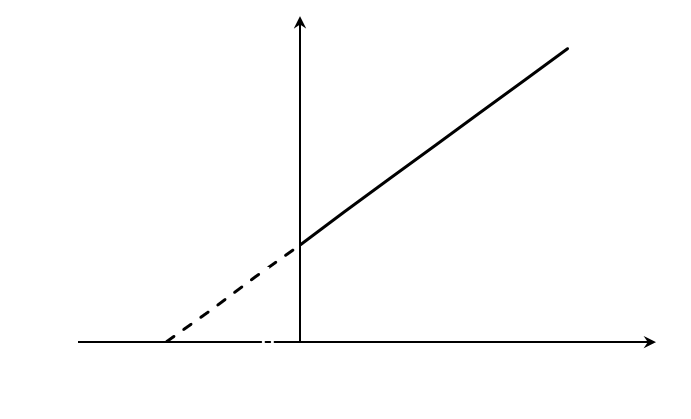
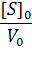
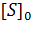
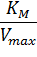
Рисунок 2 – Зависимость начальной скорости реакции от начальной концентрации субстрата в координатах уравнения Хейнса.
Существует еще один вариант преобразования уравнения Михаэлиса-Ментен. Для его осуществления избавляются от знаменателя, умножив на него обе части исходного уравнения и делят обе части на 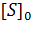
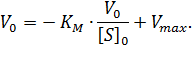 |
(4) |
Мы получили уравнение Иди-Хофсти. Его графиком является прямая в координатах V0 от [S]0/V0, из уравнения линейной регрессии которой можно определить те же кинетические параметры — Vmax и KM в соответствии с рисунком 3.
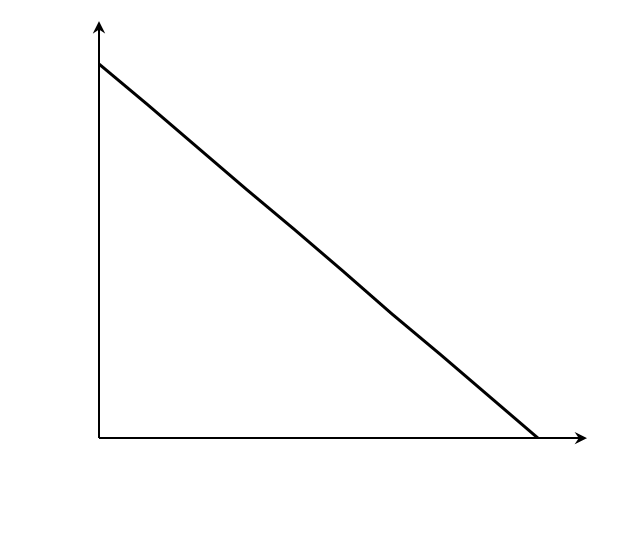
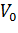
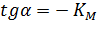
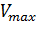
Рисунок 3 – Зависимость начальной скорости реакции от начальной концентрации субстрата в координатах уравнения Иди-Хофсти.
Статистический анализ показывает, что методы Хейнса и Иди-Хофсти дают более точные результаты, чем метод Лайнуивера-Берка. Причиной этого является то, что в первых двух графиках и зависимые, и независимые переменные входят в величины, откладываемые на обеих осях координат.
Нередко наблюдается спрямление экспериментальных данных в координатах уравнения Лайнуивера-Берка и невозможность такого преобразования по остальным уравнениям. Это говорит о том, что результаты, полученные посредством одной линеаризации, не слишком надежды и необходимо применять все три одновременно.
Очень точный графический метод – «прямой график» Эйзенталя-Боудена. Каждой начальной концентрации субстрата [S]i соответствует значение начальной скорости Vi (i = 1,2,…n). Значения [S]i с обратным знаком откладываются на оси абсцисс, на оси ординат – значения Vi. Через полученные пары точек проводят прямые, пересекающие координатные оси в точках (-[S]i, 0) и (0, Vi). Проекция общей точки пересечения прямых на горизонтальную ось равна КМ, а на вертикальную – Vmax (рисунок 4).
Разброс экспериментальных данных в этом методе учитывают с помощью нахождения медианы (в случае непрерывных распределений медианой является место, выше и ниже которого находится по 50% экспериментальных значений; другими словами, значения, лежащие ниже и выше медианы, встречаются с вероятностью 0,5).
 |
| Рисунок 4 – Определение констант уравнения Михаэлиса-Ментен по методу Корниш-Боудена. |
Для определения максимальной скорости и константы Михаэлиса применяют также метод Диксона, согласно которому точку начала координат соединяют прямыми линиями с точками на кривой уравнения Михаэлиса-Ментен, соответствующими значениям 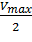
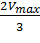
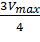
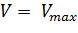
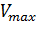
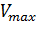
— если рассчитанная 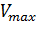
— если рассчитанная 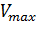
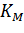
То есть, метод позволяет установить точность определения 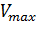
Анализируя графическим методом, проведем касательную к кривой в координатах уравнения Михаэлиса-Ментен. Для этого необходимо продифференцировать уравнение и подставить в полученную функцию значение концентрации в той точке, касательная к которой необходима – это точка (0;0), так что 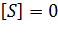
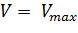
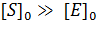
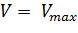
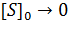
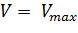
Кинетика и термодинамика ферментативных реакций (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 |
Министерство образования и науки Российской Федерации
Сибирский федеральный университет
Кинетика и термодинамика ферментативных реакций
к практическим занятиям
Специальность 020208.65 — Биохимия
Кинетика и термодинамика ферментативных реакций: Сборник задач к практическим занятиям /[Текст] / сост. . – Красноярск: Сиб. федер. ун-т, 2012. – 64 с.
Сборник задач по курсу «Кинетика и термодинамика ферментативных реакций» составлен в соответствии с программой курса и является учебно-методическим руководством по решению задач по кинетическим свойствам ферментов.
В учебном пособии представлены четко структурированные задачи по основному разделу курса «Кинетика ферментативных реакций» разной степени сложности. Предназначено для студентов биологических и медико-биологических специальностей университетов.
В ферментативной кинетике концепция стационарности применима к концентрациям связанных с ферментом интермедиатов. Когда фермент смешивается с избытком субстрата наблюдается начальный период, известный как предстационарное состояние, в течение которого концентрации этих интермедиатов достигают стационарного уровня. По достижении интермедиатами стационарных концентраций скорость реакции относительно медленно изменяется со временем и именно в данный период традиционно измеряют скорости энзиматических реакций.
Стационарное состояние является аппроксимацией, поскольку субстрат постепенно превращается в ходе эксперимента. Но, принимая во внимание, что измерения осуществляются за короткий промежуток времени, когда концентрация субстрата изменяется незначительно, стационарное состояние является хорошей аппроксимацией. Хотя изучение предстационарной кинетики позволяет анализировать механизмы ферментативного катализа, стационарная кинетика более важна для измерения каталитической активности фермента при стационарных состояниях в клетке.
Раздел 1. Уравнение Михаэлиса-Ментен
Браун (Brown A. J.) и затем В. Анри (Henri V.) в начале ХХ века высказали предположение о том, что в основе ферментативной реакции лежит обратимое взаимодействис субстрата с ферментом с образованием комплекса, который далее распадается с образованием продуктов реакции и регенерацией исходного фермента. Эта гипотеза была далее развита в работах Михаэлиса (L. Michaelis) и Ментен (M. L. Menten) (1913 г.) и позднее – Бригсом (G. E. Briggs) и Холденом (J. B.S. Haldane) (1925 г.).
Кинетическую схему простейшей односторонней ферментативной реакции превращения одного субстрата в продукт можно представить следующим образом:

Ферментативная реакция протекает в два этапа. На первом этапе фермент и субстрат образуют фермент-субстратный комплекс ES. Этот этап является быстрым и обратимым, он не сопровождается какими-либо химическими изменениями субстрата. Константы скорости реакции образования фермент-субстратного комплекса и обратного его распада равны соответственно k+1 и k-1. В образовании фермент-субстратного комплекса (ФСК, комплекс Михаэлиса) принимают участие нековалентные взаимодействия.
Каталитический процесс осуществляется на втором этапе реакции с константой первого порядка k+2 (kcat, число оборотов фермента). Комплекс Михаэлиса распадается с образованием конечного продукта реакции Р и регенерацией исходного фермента. Распад фермент-субстратного комплекса может происходить по-разному: в данной кинетической схеме он распадается в одну стадию, но в других случаях этих стадий может быть несколько.
Исходя из уравнения (1), можно расписать уравнения для скоростей отдельных стадий реакции.
Скорость образования фермент-субстратного комплекса:

Скорость обратной реакции (диссоциации комплекса на исходные вещества):

Скорость распада комплекса ES с образованием продуктов реакции и регенерацией фермента:

Стационарное течение процесса возможно тогда, когда концентрация субстрата существенно превосходит концентрацию фермента ([S]>> [E]). В этом случае распад комплекса ES по реакциям (+2) и (-1) уравновешивается его образованием по реакции (+1). Поэтому для условия стационарности можно записать:

Обозначив общую концентрацию фермента через [E]0, при условии, что [E]0 = [E] + [ES], преобразуем предыдущее уравнение

Откуда концентрация фермент-субстратного комплекса будет равна



Скорость ферментативной реакции, измеряемая согласно схеме (1) по образованию продукта реакции Р из комплекса ES, может быть выражена следующим образом

Подставляя в это выражение найденное значение [ES], получаем
Данное уравнение отражает зависимость скорости ферментативной реакции от концентрации фермента и субстрата. Константа Км носит название константы Михаэлиса и имеет размерность концентрации субстрата. Уравнение (2) свидетельствует, что зависимость скорости ферментативной реакции от концентрации субстрата при [E]0=const является гиперболической функцией (рис. 1.1).
Рис.1.1. Зависимость скорости ферментативной реакции от концентрации субстрата
Кривая представляет собой равнобочную гиперболу. При достаточно малых концентрациях субстрата, когда [S] > Км, можно принять, что Км + [S] ≈ [S], и тогда
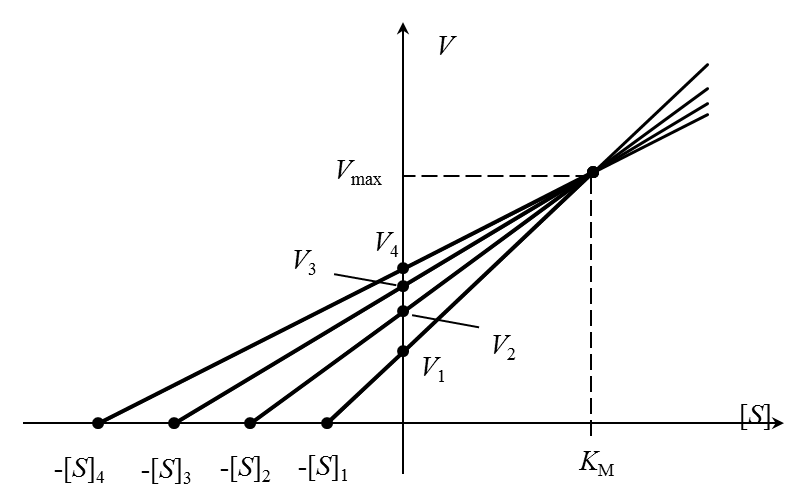
а реакция имеет нулевой порядок по отношению к субстрату. Следовательно, при достижении определенной концентрации субстрата скорость ферментативной реакции достигает максимального значения Vmax и при дальнейшем увеличении концентрации субстрата не изменяется.
Смысл такого рода зависимости очевиден: скорость ферментативной реакции определяется в целом концентрацией фермент-субстратного комплекса и при малых концентрациях субстрата концентрация комплекса Михаэлиса пропорциональна [S], тогда как при избытке субстрата фактически весь фермент находится в форме ES. Дальнейшее повышение концентрации субстрата не приводит к увеличению [ES].
С учетом приведенного выше выражения, окончательное уравнение зависимости скорости ферментативной реакции от концентрации фермента и субстрата приобретает вид

Уравнение (3) является фундаментальным уравнением ферментативной кинетики и обычно называется уравнением Михаэлиса-Ментен.
Скорость реакции приближается к максимальной достаточно медленно, и даже при [S]= 10Км, величина скорости достигает только 0,91 Vmax. В связи с этим значение максимальной скорости очень часто трудно измеримо и его приходится рассчитывать из скоростей, наблюдаемых при концентрациях субстрата ниже насыщающих.
1.1. Характеристика кинетических констант
В уравнении Михаэлиса есть два кинетических параметра, имеющих важное значение для характеристики любого фермента. Это константа Михаэлиса и максимальная скорость реакции. Константа Михаэлиса определяется соотношением констант (k—1+k+2/k+1), а величина Vmax, называемая максимальной скоростью, ‒ произведением k+2 [E]0.
Константа Михаэлиса численно равна концентрации субстрата, при которой начальная скорость ферментативной реакции равна половине максимальной. Высокое сродство фермента к субстрату характеризуется низкой величиной Кm и наоборот, низкое сродство – высокой величиной Км.
Величина Vmax не является фундаментальной характеристикой фермента, поскольку зависит от его концентрации. Если концентрация фермента известна, то целесообразно ввести величину kcat – каталитическую константу (или число оборотов фермента), определяемую выражением Vmax/[E]0. Для механизма Михаэлиса kcat идентична k+2, однако в общем случае лучше пользоваться менее определенным обозначением, а именно kcat.
Константу kкат называют еще «числом оборотов» поскольку она соответствует числу молекул субстрата, превращаемых в продукт одной молекулой фермента за 1 с. Отношение констант kcat/Км называют константой специфичности фермента.
1.2. Методы определения Км и Vmax
Константу Михаэлиса можно определить из графика Михаэлиса (рис.1.1), найдя графическим способом максимальную скорость и соответствующую величину концентрации субстрата, при которой скорость ферментативной реакции будет вдвое меньше Vmax. Эта величина [S] и будет Км. Таким способом можно определить только приблизительную величину константы Михаэлиса из-за трудности точного графического определения Vmax.
Более удобными являются методы, в которых осуществлена линеаризация уравнения Михаэлиса-Ментен, т. е. гиперболическая зависимость v от [S] переведена в линейную.
Для того чтобы построить такой график, необходимо определить в одинаковых условиях при различных концентрациях субстрата и [E]= const начальные скорости ферментативной реакции.
Метод Лайнуивера-Берка. Один из способов линеаризации уравнения Михаэлиса-Ментен предложили Лайнуивер и Берк (Lineweaver H., Burk D.)). Это так называемый метод двойных обратных величин. Для линеаризации необходимо взять обратные величины от левой и правой частей уравнения (), в результате чего оно преобразуется в уравнение вида
согласно которому между величинами, обратными начальной скорости (1/v, v-1) и концентрации субстрата (1/[S], [S]-1) соблюдается линейная зависимость, если механизм реакции подчиняется изложенным выше представлениям (рис.1.2).
Рис. 1.2. График зависимости 1/v от 1/[S] (график Лайнуивера-Берка)
Экспериментальная прямая пересекает ось абсцисс в точке (-1/[S] = 1/Км), а ось ординат – в точке (1/v = 1/Vмах). Тангенс угла наклона равен Км/Vмах. Этим широко пользуются для определения параметров Км и Vмах, характеризующих связывающую и каталитическую функции ферментов.
Метод Хайнса-Вульфа. В этом случае преобразуется уравнение Лайнуивера-Берка путем умножения правой и левой частей на концентрацию субстрата.
Графическая зависимость приведена на рис.1.3.
Рис. 1.3. График зависимости [S]/v от [S] (график Хайнса-Вульфа)
Это прямая с наклоном 1/Vmax, отсекающая на осях [S]/v и [S] отрезки Км/ Vmax и – Км соответственно.
Метод Иди-Хофсти. При одном из таких графических преобразований в так называемом графике Иди-Хофсти (pиc.2.3.5) строят график зависимости v от v/[S]. В этом случае точка пересечения прямой, полученной путем наилучшей линейной аппроксимации экспериментальных точек, с осью ординат соответствует Vmax, а тангенс угла наклона равен – Km. Данный способ линеаризации приведен на рис. 1.4.
Рис. 1.4. График зависимости v от v/[S] (график Эди-Хофсти)
Метод Эйзенталя и Корниш-Боудена. Много позднее Эйзенталь и Корниш-Боуден предложили иной метод графического представления результатов исследования кинетики ферментативных реакций – так называемый прямой линейный график. Уравнение Михаэлиса-Ментен они преобразовали в виде зависимости Vmax от Км:
Для любой пары значений [S] и v можно построить зависимость Vmax от Км. Она представляет прямую с наклоном, равным v/[S], и отрезками, отсекаемыми на осях Км и Vmax, соответственно равными – [S] v. Если провести прямые для нескольких пар значений [S] и v, то эти прямые пересекутся в одной точке, координаты которой дадут единственные значения Vmax от Км, удовлетворяющие всем парам значений [S] и v (рис.1.5).
Рис.1.5. Определение кинетических констант – Км и Vmax по методу Эйзенталя и Корниш-Боудена
Преимущества такого графика очевидно: для его построения не требуется никаких расчетов, он позволяет очень просто выявить ошибочные данные (такие прямые будут выпадать из основной совокупности прямых).
Уравнение Михаэлиса лежит в основе всех кинетических исследований ферментативных реакций, так как оно позволяет рассчитать количественные характеристики ферментов и проводить анализ их ингибирования. Величины Кm и Vmax являются важнейшими характеристиками ферментов и их можно определить, используя линеаризованные формы уравнения Михаэлиса-Ментен.
Графические методы для определения Vmax и Кm не являются оптимальными. В настоящее время данные ферментативной кинетики обрабатывают быстрее и более объективно с помощью компьютерных программ.
1.3. Задачи к разделу 1
Задача 1.1.. Определить кинетические параметры реакции, катализируемой фосфоглюкомутазой, исходя из данных, приведенных в табл.1.
http://poisk-ru.ru/s19025t23.html
http://pandia.ru/text/78/388/22072.php
Зависимость фермента от количества субстрата описывает ферментативная кинетика
Уравнения Михаэлиса-Ментен и Лайнуивера-Берка
Общую теорию ферментативной кинетики и зависимость активности фермента от субстрата.описали Л.Михаэлис и М.Л.Ментен, выразив его в своем уравнении. Бриггс и Холдейн усовершенствовали их уравнение, введя введя в него константу Михаэлиса (Km), определяемую экспериментально.
Уравнение Михаэлиса-Ментен показывает взаимосвязь максимально возможной скорости, реальной скорости реакции, константы Михаэлиса и концентрации субстрата. Так как пользоваться графиком, построенным в прямых координатах V и [S] для точных расчетов неудобно, то Г.Лайнуивер и Д.Бэрк преобразовали уравнение Бриггса–Холдейна в обратные координаты.
На самом деле уравнение Михаэлиса-Ментен в данном виде предложили Бриггс и Холдейн, но в честь основоположников оно носит название Михаэлиса-Ментен.
Выделяют три основных решения уравнения Михаэлиса-Ментен:
1. Концентрация субстрата равна величине константы Михаэлиса ([S] = Km).
В этом случае, решая уравнение Михаэлиса-Ментен, получаем, что скорость реакции V будет равна половине максимальной Vmax.(V = ½ Vmax).
В математическом смысле Km соответствует концентрации субстрата при которой скорость реакции равна половине максимальной. Ее биологический смысл заключается в характеристике сродства фермента к субстрату, а именно: увеличение величины Кm означает снижение сродства фермента к субстрату.
2. Концентрация субстрата значительно больше Km ([S] >> Km). В этом случае величиной Km можно пренебречь, при решении получим, что скорость реакции максимальна (плато на графике).
3. Концентрация субстрата значительно меньше Km ([S] << Km). В этом случае, знаменатель уравнения мало изменяется при изменении [S], а величина скорости реакции V прямо пропорциональна [S] (график линеен).
Curve of the Michaelis–Menten equation labelled in accordance with IUBMB recommendations
In biochemistry, Michaelis–Menten kinetics, named after Leonor Michaelis and Maud Menten, is the simplest case of enzyme kinetics, applied to enzyme-catalysed reactions of one substrate and one product. It takes the form of an equation describing the rate reaction rate 






“Michaelis-Menten plot”[edit]
Semi-logarithmic plot of Michaelis–Menten data
The plot of 












This plot is virtually never used today for estimating 

Model[edit]
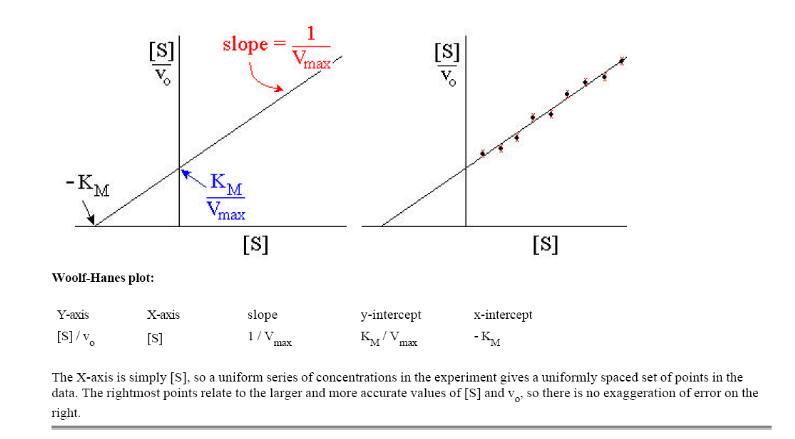
A decade before Michaelis and Menten, Victor Henri found that enzyme reactions could be explained by assuming a binding interaction between the enzyme and the substrate.[11] His work was taken up by Michaelis and Menten, who investigated the kinetics of invertase, an enzyme that catalyzes the hydrolysis of sucrose into glucose and fructose.[12] In 1913 they proposed a mathematical model of the reaction.[13] It involves an enzyme E binding to a substrate A to form a complex EA that releases a product P regenerating the original form of the enzyme.[6] This may be represented schematically as
where 


Under certain assumptions – such as the enzyme concentration being much less than the substrate concentration – the rate of product formation is given by
in which 










The Michaelis constant 
The model is used in a variety of biochemical situations other than enzyme-substrate interaction, including antigen–antibody binding, DNA–DNA hybridization, and protein–protein interaction.[17][18] It can be used to characterize a generic biochemical reaction, in the same way that the Langmuir equation can be used to model generic adsorption of biomolecular species.[18] When an empirical equation of this form is applied to microbial growth, it is sometimes called a Monod equation.
Michaelis–Menten kinetics have also been applied to a variety of topics outside of biochemical reactions,[14] including alveolar clearance of dusts,[19] the richness of species pools,[20] clearance of blood alcohol,[21] the photosynthesis-irradiance relationship, and bacterial phage infection.[22]
The equation can also be used to describe the relationship between ion channel conductivity and ligand concentration,[23] and also, for example, to limiting nutrients and phytoplankton growth in the global ocean.[24]
Specificity[edit]
The specificity constant 



If we symbolize the specificity constant for a particular substrate A as 


The reaction changes from approximately first-order in substrate concentration at low concentrations to approximately zeroth order at high concentrations.
At small values of the substrate concentration this approximates to a first-order dependence of the rate on the substrate concentration:
Conversely it approaches a zero-order dependence on 
The capacity of an enzyme to distinguish between two competing substrates that both follow Michaelis-Menten kinetics depends only on the specificity constant, and not on either 





Although both denominators contain the Michaelis constants they are the same, and thus cancel when one equation is divided by the other:
and so the ratio of rates depends only on the concentrations of the two substrates and their specificity constants.
Nomenclature[edit]
As the equation originated with Henri, not with Michaelis and Menten, it is more accurate to call it the Henri–Michaelis–Menten equation,[26] though it was Michaelis and Menten who realized that analysing reactions in terms of initial rates would be simpler, and as a result more productive, than analysing the time course of reaction, as Henri had attempted. Although Henri derived the equation he made no attempt to apply it. In addition, Michaelis and Menten understood the need for buffers to control the pH, but Henri did not.
Applications[edit]
Parameter values vary widely between enzymes. Some examples are as follows:[27]
| Enzyme |  (M) (M) |
 (s−1) (s−1) |
 (M−1s−1) (M−1s−1)
|
|---|---|---|---|
| Chymotrypsin | 1.5 × 10−2 | 0.14 | 9.3 |
| Pepsin | 3.0 × 10−4 | 0.50 | 1.7 × 103 |
| tRNA synthetase | 9.0 × 10−4 | 7.6 | 8.4 × 103 |
| Ribonuclease | 7.9 × 10−3 | 7.9 × 102 | 1.0 × 105 |
| Carbonic anhydrase | 2.6 × 10−2 | 4.0 × 105 | 1.5 × 107 |
| Fumarase | 5.0 × 10−6 | 8.0 × 102 | 1.6 × 108 |
Derivation[edit]
Equilibrium approximation[edit]
In their analysis, Michaelis and Menten (and also Henri) assumed that the substrate is in instantaneous chemical equilibrium with the complex, which implies[13][28]
in which e is the concentration of free enzyme (not the total concentration) and x is the concentration of enzyme-substrate complex EA.
Conservation of enzyme requires that[28]
where 
where 
where 



Irreversible first step[edit]
When studying urease at about the same time as Michaelis and Menten were studying invertase, Donald Van Slyke and G. E. Cullen[29] made essentially the opposite assumption, treating the first step not as an equilibrium but as an irreversible second-order reaction with rate constant 
and to note that it is functionally indistinguishable from the Henri–Michaelis–Menten equation. One cannot tell from inspection of the kinetic behaviour whether 


Steady-state approximation[edit]
G. E. Briggs and J. B. S. Haldane undertook an analysis that harmonized the approaches of Michaelis and Menten and of Van Slyke and Cullen,[30][31] and is taken as the basic approach to enzyme kinetics today. They assumed that the concentration of the intermediate complex does not change on the time scale over which product formation is measured.[32] This assumption means that 
where
This is the generalized definition of the Michaelis constant.[33]
Assumptions and limitations[edit]
All of the derivations given treat the initial binding step in terms of the law of mass action, which assumes free diffusion through the solution. However, in the environment of a living cell where there is a high concentration of proteins, the cytoplasm often behaves more like a viscous gel than a free-flowing liquid, limiting molecular movements by diffusion and altering reaction rates.[34] Note, however that although this gel-like structure severely restricts large molecules like proteins its effect on small molecules, like many of the metabolites that participate in central metabolism, is very much smaller.[35] In practice, therefore, treating the movement of substrates in terms of diffusion is not like to produce major errors. Nonetheless, Schnell and Turner consider that is more appropriate to model the cytoplasm as a fractal, in order to capture its limited-mobility kinetics.[36]
Estimation of Michaelis–Menten parameters[edit]
Graphical methods[edit]
Determining the parameters of the Michaelis-Menten equation typically involves running a series of enzyme assays at varying substrate concentrations 

Before computing facilities to perform nonlinear regression became available, graphical methods involving linearisation of the equation were used. A number of these were proposed, including the Eadie–Hofstee plot of 









However, while useful for visualization, all three linear plots distort the error structure of the data and provide less precise estimates of 







The direct linear plot is a graphical method in which the observations are represented by straight lines in parameter space, with axes 







Weighting[edit]
Many authors, for example Greco and Hakala,[47] have claimed that non-linear regression is always superior to regression of the linear forms of the Michaelis-Menten equation. However, that is correct only if the appropriate weighting scheme is used, preferably on the basis of experimental investigation, something that is almost never done. As noted above, Burk[45] carried out the appropriate investigation, and found that the error structure of his data was consistent with a uniform standard deviation in 

Uniform standard deviation of 





Uniform coefficient variation of 






Ideally the 

Closed form equation[edit]
Santiago Schnell and Claudio Mendoza suggested a closed form solution for the time course kinetics analysis of the Michaelis–Menten kinetics based on the solution of the Lambert W function.[52]
Namely,
where W is the Lambert W function and
The above equation, known nowadays as the Schnell-Mendoza equation,[53] has been used to estimate 

Reactions with more than one substrate[edit]
Only a small minority of enzyme-catalysed reactions have just one substrate, and even the number is increased by treating two-substrate reactions in which one substrate is water as one-substrate reactions the number is still small. One might accordingly suppose that the Michaelis–Menten equation, normally written with just one substrate, is of limited usefulness. This supposition is misleading, however. One of the common equations for a two-substrate reaction can be written as follows to express 


the other symbols represent kinetic constants. Suppose now that 

This has exactly the form of the Michaelis–Menten equation
with apparent values 

Linear inhibition[edit]
The linear (simple) types of inhibition can be classified in terms of the general equation for mixed inhibition at an inhibitor concentration 
in which 

Pure non-competitive inhibition is very rare, being mainly confined to effects of protons and some metal ions. Cleland recognized this, and he redefined noncompetitive to mean mixed.[57] Some authors have followed him in this respect, but not all, so when reading any publication one needs to check what definition the authors are using.
In all cases the kinetic equations have the form of the Michaelis–Menten equation with apparent constants, as can be seen by writing the equation above as follows:
with apparent values 

See also[edit]
- Direct linear plot
- Eadie–Hofstee plot
- Enzyme kinetics
- Functional response (ecology)
- Gompertz function
- Hanes plot
- Hill equation
- Hill contribution to Langmuir equation
- Langmuir adsorption model (equation with the same mathematical form)
- Lineweaver–Burk plot
- Monod equation (equation with the same mathematical form)
- Reaction progress kinetic analysis
- Steady state
- Victor Henri, who first wrote the general equation form in 1901
- Von Bertalanffy function
References[edit]
- ^ International Union of Biochemistry (now International Union of Biochemistry and Molecular Biology) (1982). «Symbolism and terminology in enzyme kinetics. Recommendations 1981». Eur. J. Biochem. 128 (2–3): 281–291. doi:10.1111/j.1432-1033.1982.tb06963.x.
{{cite journal}}: CS1 maint: uses authors parameter (link) - ^ International Union of Biochemistry (now International Union of Biochemistry and Molecular Biology) (1983). «Symbolism and terminology in enzyme kinetics. Recommendations 1981». Arch. Biochem. Biophys. 234 (2): 732–740. doi:10.1016/0003-9861(83)90262-X.
{{cite journal}}: CS1 maint: uses authors parameter (link) - ^ International Union of Biochemistry (now International Union of Biochemistry and Molecular Biology) (1982). «Symbolism and terminology in enzyme kinetics. Recommendations 1981». Biochem. J. 213 (3): 561–571. doi:10.1042/bj2130561. PMC 1152169. PMID 6615450.
{{cite journal}}: CS1 maint: uses authors parameter (link) - ^ Cornish-Bowden, A. (2014). «Current IUBMB recommendations on enzyme nomenclature and kinetics». Perspectives in Science. 1 (1–6): 74–87. Bibcode:2014PerSc…1…74C. doi:10.1016/j.pisc.2014.02.006.
- ^ The subscript max and term “maximum rate” (or “maximum velocity”) often used are not strictly appropriate because this is not a maximum in the mathematical sense.
- ^ a b Cornish-Bowden, Athel (2012). Fundamentals of Enzyme Kinetics (4th ed.). Wiley-Blackwell, Weinheim. pp. 25–75. ISBN 978-3-527-33074-4.
- ^ Busch, T.; Petersen, M. (2021). «Identification and biochemical characterisation of tyrosine aminotransferase from Anthoceros agrestis unveils the conceivable entry point into rosmarinic acid biosynthesis in hornworts». Planta. 253 (5): 98. doi:10.1007/s00425-021-03623-2. PMC 8041713. PMID 33844079. S2CID 233212717.
- ^ M. A. Chrisman; M. J. Goldcamp; A. N. Rhodes; J. Riffle (2023). «Exploring Michaelis–Menten kinetics and the inhibition of catalysis in a synthetic mimic of catechol oxidase: an experiment for the inorganic chemistry or biochemistry laboratory». J. Chem. Educ. 100 (2): 893–899. Bibcode:2023JChEd.100..893C. doi:10.1021/acs.jchemed.9b01146. S2CID 255736240.
- ^ Huang, Y. Y.; Condict, L.; Richardson, S. J.; Brennan, C. S.; Kasapis, S. (2023). «Exploring the inhibitory mechanism of p-coumaric acid on α-amylase via multi-spectroscopic analysis, enzymatic inhibition assay and molecular docking». Food Hydrocolloids. 139: 19)08524. doi:10.1016/j.foodhyd.2023.108524. S2CID 256355620.
- ^ Cárdenas, M. L.; Cornish-Bowden, A.; Ureta, T. (1998). «Evolution and regulatory role of the hexokinases». Biochim. Biophys. Acta. 1401 (3): 242–264. doi:10.1016/S0167-4889(97)00150-X. PMID 9540816.
- ^
Henri, Victor (1903). Lois Générales de l’Action des Diastases. Paris: Hermann. - ^
«Victor Henri». Whonamedit?. Retrieved 24 May 2011. - ^ a b
Michaelis, L.; Menten, M.L. (1913). «Die Kinetik der Invertinwirkung». Biochem Z. 49: 333–369.
(recent translation, and an older partial translation) - ^ a b
Chen, W.W.; Neipel, M.; Sorger, P.K. (2010). «Classic and contemporary approaches to modeling biochemical reactions». Genes Dev. 24 (17): 1861–1875. doi:10.1101/gad.1945410. PMC 2932968. PMID 20810646. - ^ a b Laidler K.J. and Meiser J.H. Physical Chemistry (Benjamin/Cummings 1982) p.430 ISBN 0-8053-5682-7
- ^ Ninfa, Alexander; Ballou, David P. (1998). Fundamental laboratory approaches for biochemistry and biotechnology. Bethesda, Md.: Fitzgerald Science Press. ISBN 978-1891786006. OCLC 38325074.
- ^
Lehninger, A.L.; Nelson, D.L.; Cox, M.M. (2005). Lehninger principles of biochemistry. New York: W.H. Freeman. ISBN 978-0-7167-4339-2. - ^ a b
Chakraborty, S. (23 Dec 2009). Microfluidics and Microfabrication (1 ed.). Springer. ISBN 978-1-4419-1542-9. - ^
Yu, R.C.; Rappaport, S.M. (1997). «A lung retention model based on Michaelis–Menten-like kinetics». Environ Health Perspect. 105 (5): 496–503. doi:10.1289/ehp.97105496. PMC 1469867. PMID 9222134. - ^
Keating, K.A.; Quinn, J.F. (1998). «Estimating species richness: the Michaelis–Menten model revisited». Oikos. 81 (2): 411–416. doi:10.2307/3547060. JSTOR 3547060. - ^
Jones, A.W. (2010). «Evidence-based survey of the elimination rates of ethanol from blood with applications in forensic casework». Forensic Sci Int. 200 (1–3): 1–20. doi:10.1016/j.forsciint.2010.02.021. PMID 20304569. - ^
Abedon, S.T. (2009). «Kinetics of phage-mediated biocontrol of bacteria». Foodborne Pathog Dis. 6 (7): 807–15. doi:10.1089/fpd.2008.0242. PMID 19459758. - ^ Ding, Shinghua; Sachs, Frederick (1999). «Single Channel Properties of P2X2 Purinoceptors». The Journal of General Physiology. 113 (5): 695–720. doi:10.1085/jgp.113.5.695. PMC 2222910. PMID 10228183.
- ^ Dugdale, RCJ (1967). «Nutrient limitation in the sea: Dynamics, identification, and significance». Limnology and Oceanography. 12 (4): 685–695. Bibcode:1967LimOc..12..685D. doi:10.4319/lo.1967.12.4.0685.
- ^
Stroppolo, M.E.; Falconi, M.; Caccuri, A.M.; Desideri, A. (Sep 2001). «Superefficient enzymes». Cell Mol Life Sci. 58 (10): 1451–60. doi:10.1007/PL00000788. PMID 11693526. S2CID 24874575. - ^ Deichmann, U.; Schuster, S.; Mazat, J.-P.; Cornish-Bowden, A. (2013). «Commemorating the 1913 Michaelis–Menten paper Die Kinetik der Invertinwirkung: three perspectives». FEBS J. 281 (2): 435–463. doi:10.1111/febs.12598. PMID 24180270. S2CID 5183178.
- ^
Mathews, C.K.; van Holde, K.E.; Ahern, K.G. (10 Dec 1999). Biochemistry (3 ed.). Prentice Hall. ISBN 978-0-8053-3066-3. - ^ a b c
Keener, J.; Sneyd, J. (2008). Mathematical Physiology: I: Cellular Physiology (2 ed.). Springer. ISBN 978-0-387-75846-6. - ^ Van Slyke, D. D.; Cullen, G. E. (1914). «The mode of action of urease and of enzymes in general». J. Biol. Chem. 19 (2): 141–180. doi:10.1016/S0021-9258(18)88300-4.
- ^
Briggs, G.E.; Haldane, J.B.S. (1925). «A note on the kinetics of enzyme action». Biochem J. 19 (2): 338–339. doi:10.1042/bj0190338. PMC 1259181. PMID 16743508. - ^ Laidler, Keith J. (1978). Physical Chemistry with Biological Applications. Benjamin/Cummings. pp. 428–430. ISBN 0-8053-5680-0.
- ^ In advanced work this is known as the quasi-steady-state assumption or pseudo-steady-state-hypothesis, but in elementary treatments the steady-state assumption is sufficient.
- ^
Murray, J.D. (2002). Mathematical Biology: I. An Introduction (3 ed.). Springer. ISBN 978-0-387-95223-9. - ^
Zhou, H.X.; Rivas, G.; Minton, A.P. (2008). «Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences». Annu Rev Biophys. 37 (1): 375–97. doi:10.1146/annurev.biophys.37.032807.125817. PMC 2826134. PMID 18573087. - ^ Mastro, A. M.; Babich, M. A.; Taylor, W. D.; Keith, A. D. (1984). «Diffusion of a small molecule in the cytoplasm of mammalian cells». Proc. Natl. Acad. Sci. USA. 81 (11): 3414–3418. Bibcode:1984PNAS…81.3414M. doi:10.1073/pnas.81.11.3414. PMC 345518. PMID 6328515.
- ^
Schnell, S.; Turner, T.E. (2004). «Reaction kinetics in intracellular environments with macromolecular crowding: simulations and rate laws». Prog Biophys Mol Biol. 85 (2–3): 235–60. CiteSeerX 10.1.1.117.1997. doi:10.1016/j.pbiomolbio.2004.01.012. PMID 15142746. - ^
Segel, L.A.; Slemrod, M. (1989). «The quasi-steady-state assumption: A case study in perturbation». SIAM Review. 31 (3): 446–477. doi:10.1137/1031091. - ^ Eadie, G. S. (1942). «The inhibition of cholinesterase by physostigmine and prostigmine». J. Biol. Chem. 146 (1): 85–93. doi:10.1016/S0021-9258(18)72452-6.
- ^ Hofstee, B. H. J. (1953). «Specificity of esterases». J. Biol. Chem. 199 (1): 357–364. doi:10.1016/S0021-9258(18)44843-0.
- ^ Hanes, C.S. (1932). «Studies on plant amylases. I. The effect of starch concentration upon the velocity of hydrolysis by the amylase of germinated barley». Biochem. J. 26 (2): 1406–1421. doi:10.1042/bj0261406. PMC 1261052. PMID 16744959.
- ^ a b Lineweaver, H.; Burk, D. (1934). «The Determination of Enzyme Dissociation Constants». Journal of the American Chemical Society. 56 (3): 658–666. doi:10.1021/ja01318a036.
- ^ The name of Barnet Woolf is often coupled with that of Hanes, but not with the other two. However, Haldane and Stern attributed all three to Woolf in their book Allgemeine Chemie der Enzyme in 1932, about the same time as Hanes and clearly earlier than the others.
- ^ This is not necessarily the case!
- ^ Lineweaver H, Burk D, Deming, W E (1934). «The dissociation constant of nitrogen-nitrogenase in Azobacter«. J. Amer. Chem. Soc. 56: 225–230. doi:10.1021/ja01316a071.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b Burk, D. «Nitrogenase». Ergebnisse der Enzymforschung. 3: 23–56.
- ^ Eisenthal, R.; Cornish-Bowden, A. (1974). «The direct linear plot: a new graphical procedure for estimating enzyme kinetic parameters». Biochem. J. 139 (3): 715–720. doi:10.1042/bj1390715. PMC 1166335. PMID 4854723.
- ^
Greco, W.R.; Hakala, M.T. (1979). «Evaluation of methods for estimating the dissociation constant of tight binding enzyme inhibitors». J Biol Chem. 254 (23): 12104–12109. doi:10.1016/S0021-9258(19)86435-9. PMID 500698. - ^ Storer, A. C.; Darlison, M. G.; Cornish-Bowden, A. (1975). «The nature of experimental error in enzyme kinetic measurements». Biochem. J. 151 (2): 361–367. doi:10.1042/bj1510361. PMC 1172366. PMID 1218083.
- ^ Askelöf, P; Korsfeldt, M; Mannervik, B (1975). «Error structure of enzyme kinetic experiments: Implications for weighting in regression-analysis of experimental-data». Eur. J. Biochem. 69 (1): 61–67. doi:10.1111/j.1432-1033.1976.tb10858.x. PMID 991863.
- ^ Mannervik, B.; Jakobson, I.; Warholm, M. (1986). «Error structure as a function of substrate and inhibitor concentration in enzyme kinetic experiments». Biochem. J. 235 (3): 797–804. doi:10.1042/bj2350797. PMC 1146758. PMID 3753447.
- ^ Cornish-Bowden, A; Endrenyi, L. (1986). «Robust regression of enzyme kinetic data». Biochem. J. 234 (1): 21–29. doi:10.1042/bj2340021. PMC 1146522. PMID 3707541.
- ^ Schnell, S.; Mendoza, C. (1997). «A closed form solution for time-dependent enzyme kinetics». Journal of Theoretical Biology. 187 (2): 207–212. Bibcode:1997JThBi.187..207S. doi:10.1006/jtbi.1997.0425.
- ^ Olp, M.D.; Kalous, K.S.; Smith, B.C. (2020). «ICEKAT: an interactive online tool for calculating initial rates from continuous enzyme kinetic traces». BMC Bioinformatics. 21 (1): 186. doi:10.1186/s12859-020-3513-y. PMC 7222511. PMID 32410570. S2CID 218624836.
- ^ Goudar, C. T.; Sonnad, J. R.; Duggleby, R. G. (1999). «Parameter estimation using a direct solution of the integrated Michaelis–Menten equation». Biochimica et Biophysica Acta (BBA) — Protein Structure and Molecular Enzymology. 1429 (2): 377–383. doi:10.1016/s0167-4838(98)00247-7. PMID 9989222.
- ^ Goudar, C. T.; Harris, S. K.; McInerney, M. J.; Suflita, J. M. (2004). «Progress curve analysis for enzyme and microbial kinetic reactions using explicit solutions based on the Lambert W function». Journal of Microbiological Methods. 59 (3): 317–326. doi:10.1016/j.mimet.2004.06.013. PMID 15488275.
- ^ According to the IUBMB Recommendations inhibition is classified operationally, i.e. in terms of what is observed, not in terms of its interpretation.
- ^ Cleland, W. W. (1963). «The kinetics of enzyme-catalyzed reactions with two or more substrates or products: II. Inhibition: Nomenclature and theory». Biochim. Biophys. Acta. 67 (2): 173–187. doi:10.1016/0926-6569(63)90226-8. PMID 14021668.
External links[edit]
Further reading[edit]
Biochemistry/Catalysis at Wikibooks










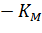
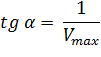
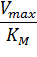
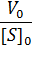














![{displaystyle {ce {E{}+A<=>[{mathit {k_{mathrm {+1} }}}][{mathit {k_{mathrm {-1} }}}]EA->[k_{ce {cat}}]E{}+P}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02a24d41daa267c3a150de51e8fcbb0ad7d5e2fb)
























