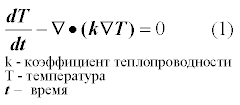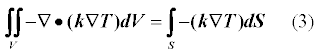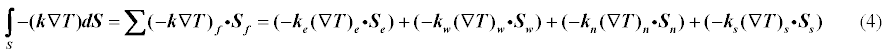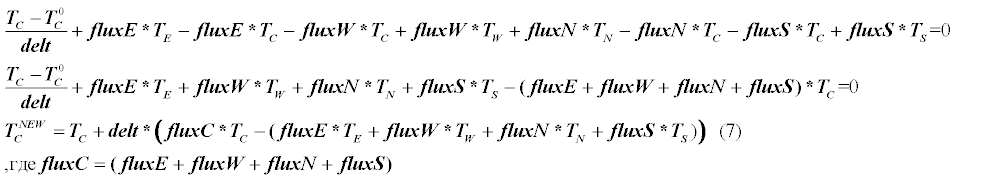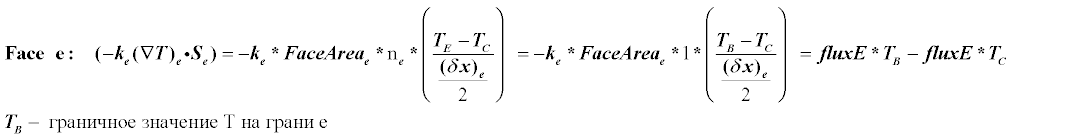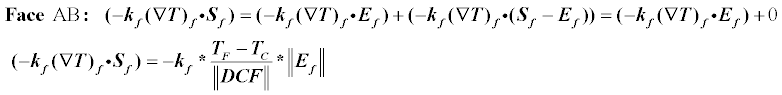Задача 1
Определить параметры газа в начальном
и конечном состояниях, изменение
внутренней энергии, теплоту, участвующую
в процессе, и работу расширения.
Теплоемкость идеального газа считать
зависящей от температуры, Исходные
данные, необходимые для решения задачи,
выбрать из таблицы 1.
Исходные данные
Процесс
– изобарный, t1
= 1500 оС,
t2
= 100 оС,
газ – О2,
Р1
= 1 МПа, m
= 2 кг.
Решение
Начальная
температура Т1
= t1
+ 273 = 1500 + 273 = 1773 К,
Конечная
температура Т2
= t2
+ 273 = 100 + 273 = 373 К.
Начальный
удельный объем находим по уравнению
состояния идеального газа ( уравнение
Клайперона)
Р1υ1
= RТ1
→
,
Газовая постоянная
для заданного газа составляет
=
= 259,8 Дж/(кг К).
Тогда начальный
объем равен
V1
= m
υ1 =
m
= 2
= 0, 92 м3.
Удельный объем
соответственно равен
υ1
= V1/
m
= 0, 92 / 2 = 0,46 м3/кг.
Н
параметры:
Р1
= 1 МПа; Т1
= 1773 К; υ1
=0,46 м3/кг;
V1
=0, 92 м3.
Определяем
конечные параметры
Температура
Т2
= 373 К – известна по условию задачи.
Так
процесс изобарный, то Р2
= Р1
= 1 МПа.
Удельный объем
определяем из уравнения Клайперона или
из закона Гей – Люссака
=
0,46
= 0,09 м3/кг.
Конечный объем
V2
= m
υ2 =
2 · 0,09 = 0,18 м3.
Конечные параметры
Р2
= 1 МПа; Т1
= 373 К; υ1
=0,09 м3/кг;
V2
=0,18 м3.
Работа расширения
L1-2
= m·
l
= m·
P
(υ2 —
υ1)
= P
(V2
— V1)
= 2· 1000 (0,09 — 0,18) = — 180 кДж.
Знак « — » показывает,
что работа затрачена .
Изменение внутренней
энергии
Δ
u
= m·
(t2
— t1)
= 2· 1,03 (100 — 1500) = — 2884 кДж.
Определим
среднюю массовую изохорную теплоемкость
в интервале температур t2
÷
t1
По таблице
справочных данных для заданного газа
при
t2 =
100 оС
= 0,87 кДж/(кг К) ;
при
t1 =
1500 оС
= 1,02 кДж/(кг К) .
Тогда
=
1,03 кДж/(кг К).
Знак
«+» показывает, что внутренняя энергия
увеличивается.
Количество теплоты
определим из уравнения первого закона
термодинамики
Q1-2
= Δ
u
+ L1-2
= -2884 — 180 = — 3064 кДж.
Знак «-» показывает,
что теплота отводится.
Задача 2
Водяной пар с начальными параметрами
Р1 = 5 МПа и χ1 = 0,9 нагревается
при постоянном давлении до температуры
t2 , затем дросселируется до давления
Р3. При давлении Р3 пар
поступает в сопло Лаваля, где расширяется
изоэнтропно (s = const) до давления Р4
= 0, 005 МПа. Определить, используя is –
диаграмму водяного пара: количество
теплоты, подведенной к пару в процессе
изобарного нагрева 1,2; изменение
внутренней энергии, а также конечную
температуру t3 в процессе
дросселирования 2-3; конечные параметры
и скорость на выходе из сопла Лаваля, а
также расход пара в процессе изоэнтропного
истечения 3-4, если известна площадь
минимального сечения сопла fмин
. Все процессы изобразить в is – диаграмме
(без масштаба, но наглядно) и дать
пояснения (как найдены точки 1, 2, 3, 4 и 4!
и соответствующие параметры). Данные,
необходимые для решения задачи, выбрать
из таблицы 2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Закон Бойля утверждает, что объем газа увеличивается при уменьшении давления при постоянной температуре.
Калькулятор расчета Закона Бойля / Мариотта
Закон Бойля / Мариотта:
Уравнение: PiVi = PfVf
где,
- Начальное давление (Pi) = PfVf / Vi
- Начальный объем (Vi) = PfVf / Pi
- Конечное давление (Pf) = PiVi / Vf
- Конечный объем (Vf) = PiVi / Pf
Пример 1: определенное количество газа содержит объем 4 л на 100 кПа. Найти давление газа, если он занимает 15 л в емкости.
Pi = 100 кПа, Vi = 4 л, Vf = 15 L
Шаг 1: Замена значения конечного давления:
Конечное давление (Pf) = PiVi / Vf
= (100 х 4) / 15
= 400/15
Конечное давление (Pf) = 26,67 кПа
Пример 2: Найти конечный объем газа, от 8 л газа на 150 кПа, пока давление составляет 125 кПа.
Pi = 150 кПа, Vi = 8 L, Р = 125 кПа
Шаг 1: Замена значения в уравнении объема:
Конечный объем (V) = PiVi / Pf
= (150х8) / 125
= 1200/125
Конечный объем (V) = 9,6 L
людей нашли эту статью полезной. А Вы?
Время на прочтение
9 мин
Количество просмотров 29K
В статье описывается реализация известного метода конечных объемов для численного решения уравнений в частных производных.Используется разбиение области на любые стандартные элементы(конечные объемы) — треугольники, четырехугольники и т.д.Метод визуализации результатов расчетов также самописный.
Метод Finite Volume (FVM)
В основе метода лежит разбиение области на непересекающиеся контрольные объемы(элементы), узловые точки, в которых ищется решение.Узловые точки находятся в центрах контрольных объемов.Также, как и для метода конечных разностей, для каждого элемента составляется уравнение, получается система линейных уравнений.Решая ее — находим значения
искомых переменных в узловых точках.Для отдельного элемента уравнение получается путем интегрирования исходного дифф уравнения по элементу и аппроксимации интегралов.
Термин конечный объем в статье будет часто заменятся на Элемент, будем для удобства считать их эквивалентами (элемент в данной статье не имеет ничего общего с методом конечных элементов).
Есть 2 различных способа решения задачи по FVM:
1) грани контрольного объема совпадают с гранями элемента
2) грани контрольного объема проходят через центры граней элементов(на которые разбита область).Искомые переменные хранятся в вершинах этих элементов.Вокруг каждой вершины строится контрольный объем. Для непрямоугольной сетки этот способ имеет еще 2 подвида.
Мы будем использовать способ 1) с контрольными объемами совпадающими с элементами на которые разбита область.
Некоторые плюсы FVM:
- сохранение основных величин по всей области, таких как энергия системы, масса, тепловые потоки и тд.Причом это условие выполняется даже для грубой расчетной сетки
- высокая скорость расчета.Многие расчетные величины можно вычислить при разбиении области на элементы, и вычислять их на каждом шаге по времени нет необходимости.
- легкость использования для задач со сложной геометрией и криволинейными границами.Легкость использования разных геометрических типов элементов — треугольники, полигоны.
Метод FVM реализуем на примере уравнения теплопроводности:
Итак основные шаги при реализации FVM:
- Перевод дифф уравнения в форму пригодную для FVM — интегрирование по контрольному объему
- Составление дискретного аналога, выбор способа перевода производных и других подынтегральных выражений в дискретную форму
- Получение уравнения для каждого из контрольных объемов, на которые разбита область.Составление системы линейных уравнений и ее решение.
Дискретизация по времени.
Для производной по времени используем стандартный простейший метод Эйлера.Это будет явная схема по времени, где берутся искомые с предыдущего шага.А на первом шаге задаются как начальные условия.
Немного теории или первый шаг в реализации FVM
Используя теорему о дивергенции интеграл по объему преобразуется в интеграл по площади.Смысл в том что интегрирование по всему внутреннему объему нашего элемента мы заменяем на интегрирование только по поверхности этого объема.Эта формулировка больше подходит для 3D случая.Для 2D у нас будет вместо объема V — площадь элемента, а вместо S — периметр элемента.Тоесть получается что интеграл по площади заменяется интегралом по периметру.Фактически у нас понижается степень производной.Если например была вторая производная то остается только первая, если была первая — то вместо производной будет искомая переменная.Надо только не забывать что имеем дело не с обычной производной а с дивергенцией.
Итак второй терм в нашем уравнении после интегрирования преобразуется так:
FVM на стандартной прямоугольной сетке
На рисунке изображен Элемент С и его соседние элементы справа(E), слева(W), сверху(N) и снизу(S).У элемента С есть 4 грани обозначенные буквами e w n s.Именно эти 4 грани и составляют периметр элемента и по ним производится интегрирование.Для каждого элемента в результате получаем дискретный аналог исходного дифф уравнения.
Составим дискретный аналог для элемента С.Для начала нужно разобраться с интегралом (3).Интеграл это ведь по факту сумма.Поэтому мы и заменяем интеграл по всей поверхности элемента, на сумму по 4-м составляющим этой поверхности, тоесть 4 граням элемента.
Индексы e w n s здесь обозначают что выражение или переменная вычисляется в центре соответствующей грани.
Теперь соберем вместе полученные упрощения частей исходного дифф уравнения — термы (2) и (4).Получим первую ступень аппроксимации:
Теперь нам осталось только до конца аппроксимировать (4), поскольку туда входит градиент, его то нам и надо перевести в численную форму.Фактически эта сумма представляет сумму потоков тепла через грани.Наш случай упрощается для прямоугольной сетки, т.к у нормали к грани остается только 1 компонент — либо вдоль оси х либо вдоль y.
Разберем подробно этот процесс на примере грани e.
Теперь подставим вместо суммы в уравнении (5) полученные дискретные аналоги для 4-х граней:
Уравнение (7) и есть конечное уравнение для элемента С, из него мы на каждом шаге по времени получаем новое значение температуры (Tnew) в элементе С.
Граничные условия на прямоугольной сетке
На рисунке показан элемент С у которого грань e находится на границе и значения температуры на этой грани известны — либо как заданная температура либо как заданный поток тепла через грань.
Мы рассмотрим только 2 вида граничных условий.
- Задана температура Tb на границе
- Задан поток FluxB на границе, рассмотрим только случай когда FluxB=0, т.е. грань e будет теплоизолирована(Insulated)
Случай 2) самый простой, поскольку получается что грань e не потребуется при дискретизации(т.к. все коэффициенты Flux=0) и можно ее просто пропустить.
Теперь рассмотрим случай 1).Дискретизация грани e будет в целом похожа на ту что уже была описана.Будут только 2 изменения — вместо Te будет известное граничное значение Tb и вместо расстояния DXe будет DXe/2.В остальном можно рассматривать значение Te так, как будто это был бы обычный соседний узел E.Теперь подробнее распишем терм для граничного элемента С.
Пример численных расчетов на прямоугольной сетке
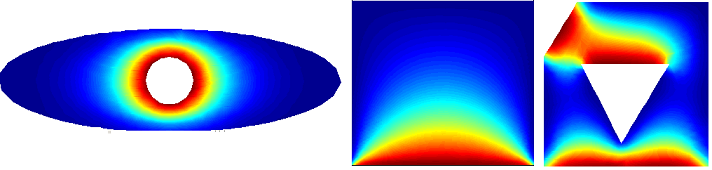
В качестве примера рассмотрим область разбитую на 9 элементов, сетка 3*3.На первых слайдах применены следующие граничные условия: по 3 сторонам температура T=0, снизу задана температура T=240.На второй строке слайдов по бокам заданы граничные условия с потоком Flux=0, сверху T=0, снизу T=240.По каждому случаю 2 картинки, одна с разбивкой области 3*3 элемента, вторая 40*40.
Код расчетов для обоих случаев (в исходниках называется heat2dminimum )
public void RunPhysic()
{
double Tc, Te, Tw, Tn, Ts;
double FluxC, FluxE, FluxW, FluxN, FluxS;
double dx = 0;
double Tb = 240;
double Tb0 = 0;
int i, j;
for (i = 0; i < imax; i++)
for (j = 0; j < jmax; j++)
{
Tc = T[i, j];
dx = dh;
if (i == imax - 1) { Te = Tb0; dx = dx / 2; }
else
Te = T[i + 1, j];
FluxE = (-k * FaceArea) / dx;
if (i == 0) { Tw = Tb0; dx = dx / 2; }
else
Tw = T[i - 1, j];
FluxW = (-k * FaceArea) / dx;
if (j == jmax - 1) { Tn = Tb0; dx = dx / 2; }
else
Tn = T[i, j + 1];
FluxN = (-k * FaceArea) / dx;
if (j == 0) { Ts = Tb; dx = dx / 2; }
else
Ts = T[i, j - 1];
FluxS = (-k * FaceArea) / dx;
FluxC = FluxE + FluxW + FluxN + FluxS;
T[i, j] = Tc + delt * (FluxC * Tc - (FluxE * Te + FluxW * Tw + FluxN * Tn + FluxS * Ts));
}
}
//Insulated
public void RunPhysic2()
{
double Tc, Te, Tw, Tn, Ts;
double FluxC, FluxE, FluxW, FluxN, FluxS;
double dx = 0;
double Tb = 240;
double Tb0 = 0;
int i, j;
for (i = 0; i < imax; i++)
for (j = 0; j < jmax; j++)
{
Tc = T[i, j];
dx = dh;
Te = 0; Tw = 0;
if (i == imax - 1)
FluxE = 0;
else
{
Te = T[i + 1, j];
FluxE = (-k * FaceArea) / dx;
}
if (i == 0)
FluxW = 0;
else
{
Tw = T[i - 1, j];
FluxW = (-k * FaceArea) / dx;
}
if (j == jmax - 1) { Tn = Tb0; dx = dx / 2; }
else
Tn = T[i, j + 1];
FluxN = (-k * FaceArea) / dx;
if (j == 0) { Ts = Tb; dx = dx / 2; }
else
Ts = T[i, j - 1];
FluxS = (-k * FaceArea) / dx;
FluxC = FluxE + FluxW + FluxN + FluxS;
T[i, j] = Tc + delt * (FluxC * Tc - (FluxE * Te + FluxW * Tw + FluxN * Tn + FluxS * Ts));
}
}
FVM в задачах со сложной геометрией
Здесь как раз проявляется преимущество FVM, где также, как и в методе конечных элементов, можно представлять область с круглыми границами через разбиение на треугольники или любые другие полигоны.Но FVM имеет еще 1 плюс — при переходе от треугольников к полигонам с большим числом сторон не требуется абсолютно ничего менять, конечно если код был написан для произвольного треугольника а не равностороннего.Более того, можно без изменения кода использовать смесь разных элементов — треугольники, полигоны, квадраты и тд.
Рассмотрим общий случай, когда вектор соединяющий центры 2-х элементов не совпадает с вектором нормали к общей грани этих элементов.Вычисление потока flux через грань теперь будет состоять из 2-х частей.В первой будет расcчитываться ортогональная составляющая а во второй так называемая «кросс-диффузия».
На картинке изображены 2 элемента, С — текущий рассматриваемый элемент и F — соседний элемент.Опишем дискретизацию для грани, разделяющей эти 2 элемента.Вектор соединяющий центры элементов — DCF.Вектор e — это единичный вектор по направлению DCF.Вектор Sf — направлен по нормали к грани, его длинна равна длине грани.
Схема расчетов выглядит примерно так.
Второй терм здесь это кросс-диффузия, она будет тем больше, чем больше расхождение между векторами Ef и Sf, если они совпадают, то она равна 0.
Распишем сначала ортогональную часть(способ minimum correction).
В исходниках я не стал реализовывать терм с кроссдиффузией, т.к встал вопрос — как проверить корректность такой реализации.Визуально сравнение результатов Матлаб и моих ничем не отличалось в отсутствии кросс-диффузии.Видимо это связано с тем что Матлаб любит треугольники близкие к равносторонним, что в итоге делает кроссдиффузию=0.Возможно позже еще вернусь к этому вопросу.
Расчет граничных элементов ничем не отличается от расчетов не на границе, вместо центра соседнего элемента берется центр грани, ну и как обычно подставляется температура на границе.
В моей реализации в итоге получается так:
Код расчетов для произвольного полигона (в исходниках называется heat2PolyTeach )
public void Calc()
{
double bc, ac;
double sumflux;
double[] aa = new double[6];
double[] bb = new double[6];
int e;
for (e = 0; e < elementcount; e++)
{
Element elem = elements[e];
int nf;
bc = 0;
ac = 0;
sumflux = 0;
for (int nn = 0; nn <6; nn++)
{
aa[nn] = 0;
bb[nn] = 0;
}
for (nf = 0; nf < elem.vertex.Length; nf++)
{
Face face = elem.faces[nf];
Element nb = elem.nbs[nf];
if (face.isboundary)
{
if (face.boundaryType == BoundaryType.BND_CONST)
{
double flux1;
double flux;
flux1 = elem.k * (face.area / elem.nodedistances[nf]);
Vector2 Sf = face.sf.Clone();
Vector2 dCf = elem.cfdistance[nf].Clone();
if (Sf * dCf < 0)
Sf = -Sf;
//1) minimum correction
//Vector2 DCF = elem.cndistance[nf].Clone();
Vector2 e1 = dCf.GetNormalize();
Vector2 EF = (e1 * Sf) * e1;
flux = elem.k * (EF.Length() / dCf.Length());
ac += flux;
bc += flux * face.bndu;
bb[nf] = flux;
}
else if (face.boundaryType == BoundaryType.BND_INSULATED)
{
double flux;
flux = 0;
ac += flux;
bc += flux * face.bndu;
bb[nf] = flux;
}
}
else
{
double flux1;
double flux;
flux1 = -elem.k * (face.area / elem.nodedistances[nf]);
Vector2 Sf = face.sf.Clone();
Vector2 dCf = elem.cfdistance[nf].Clone();
if (Sf * dCf < 0)
Sf = -Sf;
Vector2 DCF = elem.cndistance[nf].Clone();
Vector2 e1 = DCF.GetNormalize();
//corrected flux
//1) minimum correction
Vector2 EF = (e1 * Sf) * e1;
flux = -elem.k * (EF.Length() / DCF.Length());
sumflux += flux * nb.u;
ac += -flux;
aa[nf] = -flux;
}
}
elem.u = elem.u + delt * (bc - sumflux - ac * elem.u);
}
}
Примеры и проверка результатов
Проверка проводилась сравнением результатов в Матлаб и моей реализации. Mesh использовалась одинаковая, выгружалась из Матлаб и загружалась в прогу.На некоторые артефакты-треугольники не обращайте внимания, это просто непонятный глюк отрисовки.
Описание структуры исходников
Гитхаб с исходниками лежит тут
Основная версия в папке heat2PolyV2.То что относится к вычислительной части лежит в heat2PolyV2SrcFiniteVolume.
Вначале файла Scene2.cs — параметры которые можно менять для отображения в разных цветовых схемах, масштаб, отображение mesh и т.д.Сами примеры хранятся в heat2PolyV2binDebugDemos
Выгрузку из Матлаба сделать просто — нужно открыть pde toolbox, открыть m файл (либо создать самому с нуля), зайти в меню Mesh-Экспорт mesh, нажать ОК; перейти в основной Матлаб, в панельке появятся переменные — матрицы p e t, открыть файл savemymesh.m, выполнить его, появится файл p.out, перенести его в папку Demos.
В исходниках для выбора примера необходимо задать имя файла в строке param.file = «p»;(FormParam.cs).Далее необходимо применить граничные условия — для готовых примеров можно просто раскомментировать соответствующие блоки в MainSolver.cs:
//p.out
public void SetPeriodicBoundary()
Смысл тут простой — Матлаб разделяет границы по доменам, например внешние и внутренние.Также для каждого домена границы разбиты на части (группы), чтобы можно было задавать условия на участках границы по отдельности — например справа или снизу.
Возможно и вовсе не использовать Матлаб, а вручную прописать все элементы(треугольники) и их вершины + грани(только для граничных элементов)
Описание структуры файла .out
Файл разбит на секции — ##Points (вершины),##Triangle(треугольники) и ##Boundary(грани — только те которые на границе)
##Points — координаты точек, первая строка — х, вторая -y.
##Triangle — треугольники, первая строка — индекс 1-ой вершины в массиве ##Points,2 и 3 строки — индексы 2 и 3 вершины треуольника.
##Boundary — грани, первая строка — индекс 1-ой вершины грани ,2-я — индекс второй вершины, пятая строка — группа, шестая — домен
Описание папок с исходниками
Исходники написаны на Visual Studio 2010 c#.Использовался Матлаб R2012a.
Гитхаб с исходниками
- heat2PolyV2 — финальная версия
- otherheat2Utrianglestatic — реализован пример из книги p346 versteeg_h malalasekra_w_ An_introduction_to_computational_fluid…
- otherwater2dV2 — попытка решения уравнений Навье-Стокса частично используя FiniteVolume
- matlab — m файлы примеров pde toolbox + savemymesh.m который выгружает готовый .out файл для heat2PolyV2
Список книг по теме
- Versteeg HK Malalasek Introduction to computational fluid dynamics The finite volume method — уже есть второе издание
- F.Moukalled L.Mangani M.Darwish The finite volume method in computational fluid dynamics 2016г — вышла недавно (чуть ли не вчера:)
- Патанкар С.-Численные методы решения задач теплообмена и динамики жидкости-Энергоатомиздат (1984)
- Патанкар С.В.-Численное решение задач теплопроводности и конвективного теплообмена при течении в каналах-МЭИ (2003)
- Computational methods for fluid dynamics Ferziger JH Peric 2001 — хоть напрямую и не относится к FVM, но оч много полезного
Выберите значение, которое хотите получить:
Начальное давление: кпа Начальный объем: L Конечное давление: кпа Финальный объем: L
Калькулятор комбинированного газового закона
Это комбинация из пяти калькуляторов газовых законов, которые являются законом Бойля, законом Чарльза, законом Гей-Люссака, законом Авогадро. Это также может быть выведено из закона идеального газа. Другими словами, пять указанных закона также могут быть получены из этого уравнения, просто предполагая, что свойство (объем, давление или температура) является постоянным.
Калькулятор закона Бойля
Этот калькулятор закона Бойля является отличным инструментом, когда вам нужно оценить параметры газа в изотермическом процессе. Вы найдете ответ на вопрос «Что такое закон Бойля?» в тексте, поэтому читайте дальше, чтобы узнать о формуле закона Бойля, увидеть несколько полезных примеров упражнений по закону Бойля и узнать, как распознать, когда процесс удовлетворяет закону Бойля на графике.
Определение закона Бойля
Закон Бойля (также известный как закон Бойля-Мариотта) говорит нам о взаимосвязи между давлением газа и его объемом при постоянной температуре и массе газа. В нем говорится, что абсолютное давление обратно пропорционально объему.
Определение закона Бойля также можно сформулировать следующим образом: произведение давления и объема газа в замкнутой системе постоянно, пока не изменяется температура.
Закон Бойля описывает поведение идеального газа (газов, которые могут быть описаны уравнением идеального газа) во время изотермического процесса, что означает, что температура газа остается постоянной во время перехода, как и внутренняя энергия газа.
Формула закона Бойля
Мы можем записать уравнение закона Бойля следующим образом:
p₁ * V₁ = p₂ * V₂
где p₁ и V₁ – начальное давление и объем соответственно. Точно так же p₂ и V₂ являются конечными значениями этих параметров газа.
В зависимости от того, какой параметр мы хотим оценить, формулу закона Бойля можно записать по-разному. Допустим, мы изменили объем газа в изотермических условиях и хотим найти результирующее давление. Тогда уравнение закона Бойля утверждает, что:
p₂ = p₁ * V₁ / V₂ or p₂ / p₁ = V₁ / V₂
Как мы видим, отношение конечного и начального давления является обратным отношением для объемов. Этот калькулятор закона Бойля работает в любом направлении, которое вам нравится. Просто введите любые три параметра, и четвертый будет рассчитан сразу! А если вы не знаете, как рассчитать это вручную, вы можете воспользоваться нашим калькулятором коэффициентов для получения более подробной информации.
Весь процесс можно визуализировать на графике закона Бойля. Чаще всего используется тип, в котором давление зависит от объема. Для этого процесса кривая представляет собой гиперболу. Переход может происходить в обоих направлениях, поэтому и сжатие, и расширение газа удовлетворяют закону Бойля.
Примеры закона Бойля
Закон Бойля можно использовать несколькими способами, поэтому давайте рассмотрим несколько примеров:
-
Представьте, что у нас есть эластичный контейнер, в котором находится газ. Начальное давление 100 кПа (или 10⁵ Па, если использовать научную запись), а объем сосуда равен 2 м³. Решаем сжать бокс до 1 м³, но общую температуру не меняем. Вопрос: «Как меняется давление газа?». Мы можем использовать формулу закона Бойля:
p₂ = p₁ * V₁ / V₂ = 100 kPa * 2 m³ / 1 m³ = 200 kPaПосле уменьшения объема вдвое внутреннее давление удваивается. Это является следствием того, что произведение давления на объем должно быть постоянным в течение этого процесса.
-
Следующий пример закона Бойля касается газа под давлением 2,5 атм, занимающего 6 литров пространства. Затем его изотермически декомпрессируют до давления 0,2 атм. Узнаем его окончательный объем. Мы должны переписать уравнение закона Бойля:
V₂ = p₁ * V₁ / p₂ = 2.5 atm * 6 l / 0.2 atm = 75 lВы всегда можете воспользоваться нашим калькулятором закона Бойля, чтобы проверить правильность своих оценок!
Где применяется закон Бойля?
Закон Бойля описывает все процессы, при которых температура остается постоянной. В термодинамике температура — это мера средней кинетической энергии, которой обладают атомы или молекулы. Другими словами, мы можем сказать, что средняя скорость частиц газа во время этого перехода не меняется. Формула закона Бойля справедлива для широкого диапазона температур.
В расширенном режиме вы можете выбрать любую понравившуюся температуру, а мы рассчитаем количество молекул, содержащихся в газе. Вам нужно только убедиться, что вещество остается в газовой форме (например, не конденсируется и не кристаллизуется) при этой температуре.
Есть несколько областей, где применим закон Бойля:
-
Тепловая машина Карно — состоит из четырех термодинамических процессов, два из которых изотермические, удовлетворяющие закону Бойля. Эта модель может сказать нам, каков максимальный КПД тепловой машины.
Дыхание также можно описать законом Бойля — всякий раз, когда вы делаете вдох, ваша диафрагма и межреберные мышцы увеличивают объем легких, что приводит к снижению давления газа. Когда воздух течет из области более высокого давления в область более низкого давления, воздух поступает в легкие и позволяет нам получать кислород из окружающей среды. При выдохе объем легких уменьшается, поэтому давление внутри выше, чем снаружи, поэтому воздух течет в обратном направлении.
Шприц – всякий раз, когда вам нужно сделать инъекцию, врач или медсестра сначала набирают жидкость из маленького флакона. Для этого они используют шприц. При вытягивании поршня доступный объем увеличивается, что приводит к снижению давления и, согласно формуле закона Бойля, вызывает всасывание жидкости.
Другие термодинамические процессы
Закон Бойля вместе с законом Чарльза и законом Гей-Люссака входят в число фундаментальных законов, описывающих подавляющее большинство термодинамических процессов. Помимо определения значений определенных параметров, таких как давление или объем, также можно узнать кое-что о теплопередаче и работе, совершаемой газом во время этих переходов, а также об изменении внутренней энергии. Мы собрали их все в нашем калькуляторе комбинированных газовых законов, где вы можете выбрать любой процесс и оценить результаты для реальных газов.
Калькулятор закона Чарльза
Калькулятор закона Чарльза — это простой инструмент, который описывает основные параметры идеального газа в изобарном процессе. В тексте вы можете найти ответ на вопрос «Что такое закон Чарльза?», узнать, как выглядит формула закона Чарльза, и прочитать, как решать термодинамические задачи с помощью некоторых примеров закона Чарльза.
Определение закона Чарльза
Закон Чарльза (иногда называемый законом объемов) описывает взаимосвязь между объемом газа и его температурой, когда давление и масса газа постоянны. В нем говорится, что объем пропорционален абсолютной температуре.
Есть несколько других способов, которыми мы можем записать определение закона Чарльза, один из которых таков: соотношение объема и температуры газа в замкнутой системе остается постоянным до тех пор, пока давление не меняется. (Проверьте, как сделать подобные соотношения в нашем калькуляторе коэффициентов!)
Закон Чарльза описывает поведение идеального газа (газов, которые могут быть описаны уравнением идеального газа) во время изобарного процесса, что означает, что давление остается постоянным во время перехода.
Формула закона Чарльза
Основываясь на определении закона Чарльза, мы можем записать уравнение закона Чарльза следующим образом:
V₁ / T₁ = V₂ / T₂
где V₁ и t₁ — начальный объем и температура соответственно. Аналогично, V₂ и t₂ являются конечными значениями этих параметров газа.
Как работает этот калькулятор законов Чарльза? Сначала вам нужно вставить три параметра, а четвертый рассчитывается для вас автоматически. Допустим, мы хотим найти конечный объем, тогда формула закона Чарльза дает:
V₂ = V₁ / T₁ * T₂
Если вы предпочитаете установить конечный объем и хотите оценить результирующую температуру, то уравнение закона Чарльза изменится на:
T₂ = T₁ / V₁ * V₂
В расширенном режиме вы также можете определить давление и посмотреть, сколько молей атомов или молекул находится в контейнере.
Примеры закона Чарльза
Мы можем использовать калькулятор закона Чарльза для решения некоторых термодинамических задач. Давайте посмотрим, как это работает:
- Представьте, что у нас есть шар, наполненный воздухом. Его начальный объем равен 2 литрам, и он находится на пляже, где температура составляет 35°C. Затем мы перемещаем его в кондиционируемую комнату с температурой 15°C. Как изменится объем мяча?
-
Прежде всего, формула закона Чарльза требует абсолютных значений температуры, поэтому мы должны преобразовать их в кельвины: T₁ = 35°C = 308,15 K, T₂ = 15°C = 288,15 K.
-
Тогда мы можем применить уравнение закона Чарльза в форме, где оценивается конечный объем: V₂ = V₁ / T₁ * T₂ = 2 л / 308,15 К * 288,15 К = 1,8702 л.
Как мы видим, объем уменьшается, когда мяч перемещается из более теплого места в более прохладное. Иногда вы можете испытать этот эффект, меняя свое местоположение или просто оставляя объект в покое, когда погода меняется. Мяч кажется недодутым, и кому-то может показаться, что в нем есть дырка, через которую выходит воздух. К счастью, это всего лишь физика, так что вам не придется покупать еще один мяч — просто надуйте тот, который у вас есть, и наслаждайтесь! Одно крошечное замечание: воздух является примером реального газа, поэтому результат является лишь приближением, но до тех пор, пока мы избегаем экстремальных условий (давление, температура). Результат достаточно близок к реальному значению.
- Во второй задаче нагреваем легко растягивающийся контейнер. Он заполнен азотом, что является хорошим приближением к идеальному газу. Мы можем найти, что его начальный объем составляет 0,03 фута³ при комнатной температуре, 295 К. Затем мы помещаем его близко к источнику нагрева и оставляем на некоторое время. Через несколько минут его объем увеличился до 0,062 фута³. Имея все эти данные, можем ли мы оценить температуру нашего обогревателя?
-
Применим формулу закона Чарльза и перепишем в такой форме, чтобы можно было вычислить температуру:
-
Результат можно записать в более дружелюбной форме: T₂ = 336,55°C или T₂ = 637,79°F.
Это отличный пример, который показывает нам, что такое устройство можно использовать в качестве термометра! Что ж, это не очень практичный метод и, возможно, не такой точный, как обычные, но все же заставляет задуматься, а какие еще необычные применения можно получить из других повседневных предметов?
Как закон Чарльза применяется в реальной жизни?
На самом деле есть разные области, где мы можем использовать закон Чарльза. Вот список нескольких самых популярных и интересных примеров:
-
Полет на воздушном шаре – вы наверняка хоть раз в жизни видели в небе воздушный шар. Задумывались ли вы когда-нибудь, как он может летать, и почему они оборудованы огнем или другими источниками тепла на борту? Закон Чарльза — ответ! Всякий раз, когда воздух нагревается, его объем увеличивается. В результате такое же количество (масса) газа занимает большее пространство, а значит, плотность уменьшается. Плавучесть окружающего воздуха делает остальную работу, и воздушный шар начинает плавать. Рулевое управление в любом заданном направлении, вероятно, это отдельная история, но общую концепцию движения вверх и вниз можно объяснить с помощью закона Чарльза.
-
Эксперименты с жидким азотом — вы когда-нибудь видели эксперимент, в котором шарик или воздушный шар помещают внутрь контейнера, наполненного жидким азотом, а затем выносят наружу? Во-первых, он сжимается независимо от того, насколько большим он был в начале. Затем, после освобождения, он возвращается в исходное состояние. Опять же, всякий раз, когда изменяется температура, изменяется и объем.
-
Термометр – как показано в предыдущем разделе, можно сконструировать устройство, измеряющее температуру на основе закона Чарльза. Хотя мы должны знать о его ограничениях, которые в основном связаны с прочностью объектов на растяжение и устойчивостью к высоким температурам, мы можем изобрести оригинальное устройство, которое идеально подходит для наших нужд. Всякий раз, когда вы не уверены в результате, проверьте этот калькулятор закона Чарльза, чтобы найти ответ.
Другие термодинамические процессы
Закон Чарльза вместе с законом Бойля и законом Гей-Люссака входят в число фундаментальных законов, описывающих подавляющее большинство термодинамических процессов. Мы собрали все основные газовые переходы в нашем калькуляторе комбинированного газового закона, где вы можете оценить не только конечную температуру, давление или объем, но также изменение внутренней энергии или работу, выполненную газом.
Калькулятор закона Гей-Люссака
Этот калькулятор закона Гей-Люссака предоставляет вам информацию об основных параметрах газа во время изохорного перехода. В тексте вы найдете определение закона Гей-Люссака, некоторые эквивалентные формулы закона Гей-Люссака и несколько вычислительных примеров, чтобы вы знали, что полностью понимаете, что происходит. Знаете ли вы, что газовый закон Гей-Люссака применим к вашей повседневной деятельности? Ознакомьтесь с некоторыми из самых интересных!
Определение закона Гей-Люссака
Закон Гей-Люссака (также известный как закон давления) описывает взаимосвязь между давлением и температурой газа при постоянном количестве газа в закрытом и жестком контейнере. Закон гласит, что абсолютное давление прямо пропорционально температуре.
Чтобы закон Гей-Люссака выполнялся, газовый баллон должен быть сконструирован таким образом, чтобы объем газа оставался постоянным при любых условиях. Другими словами, закон Гей-Люссака говорит нам о поведении идеального газа во время изохорного (постоянного объема) процесса.
Формула закона Гей-Люссака
Используя приведенное выше определение, одну форму формулы закона Гей-Люссака можно записать следующим образом:
p₁ / T₁ = p₂ / T₂
где p₁ и T₁ – начальное давление и температура соответственно. Точно так же p₂ и T₂ являются конечными значениями этих параметров газа.
Однако это не единственная форма уравнения. Например, если вы хотите проверить взаимосвязь между начальным и конечным давлением, формула будет выглядеть так:
p₁ / p₂ = T₁ / T₂
Как видим, отношение начальной и конечной температур пропорционально отношению начального и конечного давлений.
С помощью этого калькулятора закона Гей-Люссака вы можете оценить любой из этих четырех параметров, если вы знаете три других параметра. Просто вставьте три известных значения, и последнее будет оценено мгновенно. Более того, в расширенном режиме вы также можете рассчитать количество газа в молях в зависимости от объема контейнера.
Примеры газового закона Гей-Люссака
Как насчет того, чтобы перейти к решению некоторых вычислительных задач?
- Допустим, у нас есть металлическая банка с 300 мл воздуха в комнате при 20°C, а начальное давление газа – 100 кПа (мы также можем написать 10⁵ Па, используя научную запись). Затем нагреваем наш контейнер, чтобы температура достигла 400°C. Предполагая, что банка не протекает, каково конечное значение давления внутри?
- Для начала нам нужно преобразовать температуры в абсолютную шкалу Кельвина, которая необходима для закона Гей-Люссака: T₁ = 20°C = 293,15 K, T₂ = 400°C = 673,15 K.
- Следующим шагом является изменение формулы закона Гей-Люссака для оценки конечного давления: p₂ = p₁ / T₁ * T₂ = 100 кПа / 293,15 K * 673,15 K = 229,63 кПа.
- Мы также можем оценить количество газа в молях, используя информацию, предоставленную нам в вопросе: n = p₁ * V₁ / (R * T₁) = 100 кПа * 300 мл / (8,314 Дж/(моль*К) * 293,15 К. ) = 0,0123 моль. Здесь R – газовая постоянная.
- Вы всегда можете проверить ответ с помощью нашего калькулятора закона Гей-Люссака или просто использовать его, чтобы сэкономить время!
-
В этом примере у нас есть жесткий ящик, заполненный азотом, и мы знаем, что он нагревается до 460 К, а внутреннее давление равно 1,6 атм. Через некоторое время он охлаждается до точки, когда давление падает до 1 атм. Какая конечная температура?
Ответ относительно прост — просто примените закон Гей-Люссака: T₂ = T₁ * p₂ / p₁ = 460 K * 1 атм / 1,6 атм = 287,5 K.
Небольшое замечание по поводу результатов. Мы должны знать, что обе задачи являются примерами реальных газов, тогда как все формулы точны только на 100% для идеальных газов. Однако в таких вычислительных задачах результат на самом деле является действительно хорошим приближением, поэтому, пока мы не помещаем наш газ в какие-то экстремальные условия (давление или температура), эти результаты можно использовать.
Закон Гей-Люссака в реальной жизни
Можем ли мы на самом деле увидеть, как закон Гей-Люссака работает в нашей повседневной жизни? Взгляните на эти примеры:
-
Давление в шинах в разное время года — вы когда-нибудь накачивали шину зимой, а с наступлением тепла она перекачивалась? Или, наоборот, когда он был заполнен летом, давление уменьшилось при его остывании? В этом случае шины являются примером закрытой системы, поэтому чем выше температура, тем выше давление.
-
Крышка на кастрюле — сначала это может показаться довольно очевидным, но почему крышка постоянно прыгает и гремит, пока вы разогреваете еду в кастрюле? Повышение температуры приводит к повышению давления газа (в основном водяного пара) внутри кастрюли. В какой-то момент давление становится достаточно высоким, чтобы поднять крышку, и избыток газа выпускается, давление выравнивается, и весь процесс начинается сначала, и снова…
-
Положить горячую банку в холодную воду — это простой способ проверить, верен ли закон Гей-Люссака, если вы еще не верите нам. Просто возьмите пустую металлическую банку из-под любимого напитка и безопасно подогрейте ее. Мы настоятельно рекомендуем делать это на улице, а не дома! Через непродолжительное время можно попробовать заткнуть дырку, а затем опустить банку в холодную воду. Если вы добьетесь успеха, банка сожмется из-за падения внутренней температуры, что также приведет к снижению давления внутри.
Другие термодинамические процессы
Газовый закон Гей-Люссака вместе с законами Бойля и Чарльза входят в число фундаментальных законов, описывающих подавляющее большинство термодинамических процессов. Если вас интересует оценка изменения температуры, работы, совершаемой газом, или вы просто хотите сравнить результаты для разных типов газа, вы можете проверить наш калькулятор комбинированного газового закона , где мы собрали все основные газовые переходы!
Калькулятор закона идеального газа
Этот калькулятор закона идеального газа поможет вам установить свойства идеального газа в зависимости от давления, температуры или изменения объема. Читайте дальше, чтобы узнать о характеристиках идеального газа, как использовать уравнение закона идеального газа и определение постоянной идеального газа.
Мы также рекомендуем воспользоваться нашим калькулятором комбинированного газового закона для дальнейшего понимания основных термодинамических процессов идеальных газов.
Что такое идеальный газ
Идеальный газ — это частный случай любого газа, удовлетворяющего следующим условиям:
- Газ состоит из большого количества молекул, которые беспорядочно движутся.
- Все молекулы являются точечными частицами (они не занимают места).
- Молекулы не взаимодействуют, за исключением столкновения.
- Все столкновения между частицами газа абсолютно упругие.
- Частицы подчиняются законам движения Ньютона.
Уравнение закона идеального газа
Все свойства идеального газа можно выразить одной формулой:
pV = nRT
где:
- p – давление газа, измеренное в Па;
- V — объем газа, измеренный в м³;
- n – количество вещества, измеренное в молях;
- R — постоянная идеального газа; а также
- T – температура газа, измеренная в градусах Кельвина.
Чтобы найти любое из этих значений, просто введите другие в калькулятор закона идеального газа.
Например, если вы хотите рассчитать объем 40 молей газа при давлении 1013 гПа и температуре 250 К, результат будет равен:
V = nRT/p = 40 * 8.3144598 * 250 / 101300 = 0.82 m³.
Постоянная идеального газа
Газовая постоянная (символ R) также называется молярной или универсальной постоянной. Он используется во многих фундаментальных уравнениях, таких как закон идеального газа.
Значение этой константы составляет 8,3144626 Дж/(моль·К).
Газовая постоянная часто определяется как произведение постоянной Больцмана k (которая связывает кинетическую энергию и температуру газа) и числа Авогадро (количество атомов в моле вещества):
R = NAk = (6.02214076 × 1023 /mol) * (1.38064852 × 10-23 J/K) = 8.3144626 J/(mol·K)