В этой статье мы собираемся изучить различные способы определения скорости без учета времени, а также примеры, некоторые факты и способы решения связанных проблем.
Исходя из этого, энергия объекта сохраняется; скорость объекта равна квадратному корню из удвоенного произведения его ускорения на расстояние, которое он проходит, также в зависимости от начальной скорости объекта.
Как найти конечную скорость без времени?
Ускоряющийся объект со временем меняет свою скорость.
Скорость, достигаемая объектом за период времени, пока он не перестанет ускоряться в течение этого времени, называется конечной скоростью объекта.
Давайте посмотрим, как найти конечную скорость без использования временного символа.
Рассмотрим график скорость-время, показывающий изменение скорости объекта при равномерном линейном движении во времени. Из графика видно, что время T = 0, скорость = u, а в момент времени T = t скорость = v.
Поскольку скорость — это отношение изменения положения с изменяющимся временем, смещение будет равно
х=vt — (1)
Приведенный выше график связан со смещением соотношением, показанным в уравнении (1).
Измерим площадь, покрытую объектом, общая площадь будет равна сумме площадей треугольника (∆ABC) и четырехугольника (□ ACDO).
х = Ar(∆ABC)+ Ar(∆ACDO)
=1/2 бч+фунт
=1/2 t*(vu)+ut—(3)
Поскольку ускорение равно изменению скорости со временем, т.е.
а=dv/dt — (4)
а=ву/т-0=ву/т
ву=ат—(5)
Подставляя уравнение (5) в уравнение (3)
х=1/2 t * at+ut
х=1/2 при2+ут—(6)
Таким образом,
Из уравнения (4) имеем
дв=адт
Интегрируя это уравнение, получаем
∫dv=∫dt
v = при + C
При t = 0 v = u, следовательно, C = u
Следовательно,
v=u+at —(7)
Теперь это уравнение является уравнением, зависящим от времени, а время t из приведенного выше соотношения равно
t=vu/a —(8)
Средняя скорость — это сумма всех скоростей, достигнутых объектом в разные промежутки времени, деленная на общее количество скоростей, суммированных вместе. Здесь у нас есть две скорости: начальная скорость u и конечная скорость v, поэтому средняя скорость равна
Vсредний=Vокончательный+Vначальный/Общее количество скоростей
Vсредний=(v+u)/2 — (9)
Используя уравнение (1), x=vt
Подставляя уравнения (8) и (9) в уравнение (1)
х=(v+u)/2 *(vu)/a
х=v2-u2/2а
2акс = v2-u2/2
v2=u2+2акс — (10)
Приведенное выше уравнение не зависит от времени и показывает связь между начальной скоростью объекта, постоянным ускорением и перемещением объекта.
Problem1: Мяч движется в прямолинейное движение с ускорением 2 м/с. Если начальная скорость мяча 4 м/с, то какой будет его скорость, когда он преодолеет расстояние 20 м?
Дано: a = 2 м / с
u = 4 м / с
d = 20 м
Используя уравнение (10),
v2=u2+2 оси
=42+2*2*20
= 16 + 80 = 96 м / с
поэтому v=9.8 м/с
Следовательно, когда мяч преодолеет расстояние 60 метров, скорость мяча составит 9.8 м / с.
Как определить скорость падающего объекта без учета времени?
Линейная скорость зависит от времени и представляет собой отношение изменения положения во времени.
Падение предмета сопровождается энергии внутри него, в форме кинетической энергии и потенциальной энергии, и энергия не может быть ни создана, ни исчезнуть. На основании этого факта мы можем рассчитать скорость объекта независимо от времени.
Когда объект поднимается на высота над землей приобретает некоторый потенциал энергия, которая затем преобразуется в кинетическую энергию и используется во время полета.
Рассмотрим объект массы m, который стоит на столе высотой h.1, он испытывает внешнюю силу, набирает обороты и начинает ускоряться по направлению к земле. Поскольку объект покоится на столе, его начальная скорость u = 0 и, следовательно, кинетическая энергия также равна нулю. Объект на высоте h1 имеет потенциальную энергию U1 связанные с ним.
U1= mgh1
Начиная свой путь к земле, эта потенциальная энергия преобразуется в кинетическую энергию.
KE2=1/2мВ2
После падения на землю потенциальная энергия тела U2= mgh0; так как ч0=0, U_2=0.
Поскольку энергия объекта сохраняется, сумма кинетической энергии и потенциальной энергии до и после падения на землю будет равна.
KE1+U1=КЭ2+U2
U1=КЭ2
MGH1=1/2мВ2
v2=2гх1
v = √2gh1-(Один)
Следовательно, скорость объекта, падающего на землю под действием силы тяжести, определяется уравнением (11).
Problem2: Мальчик играет с мячом. Он подбросил мяч высоко в воздух и наблюдает за его свободным падением. Какова будет скорость мяча при приближении к земле, если мяч поднимется на высоту 8 метров над поверхностью Земли?
Дано: Высота h = 8м,
g = 9.8 м / с2
Используя уравнение (11),
v = √2gh1
=√2*9.8*8
=√156.8=12.52 м/с
Следовательно, конечная скорость мяча, приближающегося к земле, будет равна 12.5 м / с.
Как найти горизонтальную скорость без времени?
Объект, движущийся в горизонтальном направлении независимо от ускорения свободного падения Земли и приложенной силы, называется горизонтальной скоростью.
Горизонтальная скорость в простоте равна отношению расстояния, пройденного объектом, и времени, затраченного на преодоление расстояния. Это,
Горизонтальная скорость VH= пройденное расстояние/затраченное время
Для объекта, движущегося в движении снаряда, объект связан с двумя компонентами скорости: горизонтальной составляющей по оси x ‘V Cosθ’ в направлении движения и вертикальной составляющей по оси y ‘V Sinθ’, действующей вверх. при ускорении вверх, а затем вниз по отрицательной оси Y при ускорении по направлению к земле.
Из приведенного выше графика, чтобы вычислить горизонтальную скорость, которая является постоянной и в направлении оси x, компонент косинуса по тригонометрии равен
Cosθ=соседний/гипотенуза=горизонтальная скорость/начальная скорость
Cosθ=VH/V
VH= V Cos θ — (12)
Вышеупомянутое соотношение показывает уравнение для определения горизонтальной скорости независимо от времени.
Пример: Мяч подбрасывается в воздух и движется по параболической траектории под углом 60 °.0 с поверхности Земли. Если начальная скорость мяча равна 5 м / с, найдите горизонтальную скорость мяча.
Дано: θ = 600
Начальная скорость u = 5 м / с
Используя уравнение,
VH=VCosθ
=5*Кос(60)
=5*1/2=2.5 м/с
Следовательно, горизонтальная скорость мяча составляет 2.5 м / с.
Дальность полета снаряда — это расстояние, которое объект преодолеет от своей начальной точки, которая находится в точке (0,0) на приведенном выше графике, в зависимости от горизонтальной скорости объекта и того, как долго объект находится в воздухе.
То есть,
Р=ВHTf-(Один)
Где R — диапазон, ВH — горизонтальная скорость объекта, а Tf время полета.
Время, необходимое объекту во время движения снаряда, чтобы вернуться на землю при y = 0, упоминается как время полета.
Выведем уравнение для времени пролета, используя уравнение прямолинейного движения, приведенное ниже.
V=U+at—(14)
Начальная скорость объекта U=VSinθ
Конечная скорость V Cosθ =0
И a = -g, поскольку ускорение находится в отрицательной оси y.
Уравнение становится,
V= V Sinθ –gt
С момента финала скорость равна нулю,
0= VSinθ –gt
V Sinθ =gt
t=V Sinθ/g — (15)
Это время, необходимое объекту для достижения максимальной высоты во время полета.
Это означает, что время достижения максимальной высоты будет равно времени, необходимому объекту для покрытия оставшейся половины полета.
Значит, время для полета
Tf=2 В Sinθ/g — (16)
Подставляя уравнение (12) и уравнение (16) в уравнение (13),
R=V Cosθ*2V Sinθ/g
Р=В2/г* 2SinθCosθ
Р=В2 Sin2θ/g — (17)
Следовательно, скорость движущегося снаряда объекта также равна
V=√Rg/Sin2θ — (18)
Скорость может быть рассчитана путем измерения дальности полета и угла, который объект составляет относительно земли.
Подробнее о Снаряд Движение.
Как найти центростремительную скорость без учета времени?
Объект, движущийся по круговой траектории со временем, приобретает центростремительную скорость.
Направление скорости объекта по круговой траектории остается касательным к окружности и перпендикулярно центростремительной силе, направленной к центру.
Рассмотрим объект массы m, ускоряющийся по круговой траектории из-за внешней силы, приложенной к объекту. Центростремительная сила, действующая на объект, прямо пропорциональна квадрату, умноженному на скорость, достигаемую объектом, и обратно пропорциональна расстоянию от объекта до центра круга. Приложенная сила равна центростремительной силе, действующей на объект.
Ф=Фc
ма=мв2/r
а=в2/r
v2=ар
v=√ar—(19)
Скорость объекта при круговом движении равна квадратному корню из ускорения объекта и радиуса круговой траектории и не зависит от времени.
Пример: Представьте машину, движущуюся по круговой дорожке за пределами футбольной площадки с ускорением 40 км / ч. Диаметр земли 80 метров. Найдите скорость автомобиля.
Given: a=40km h=40*1000/60*60=11.1m/s
d=80м, r=80/2=40м
v=√ар
=√11.1 м/с*40 м
=√444
= 21.1 м / с2
=75.96 км/ч~ 76 км/ч
Следовательно, скорость автомобиля, разгоняющегося по круговой траектории, составляет 76 км / ч.
Подробнее о Как найти скорость с ускорением: разные подходы, проблемы, примеры.
Часто задаваемые вопросы
Q1. Две девушки играют в передачу с мячом; одна девушка бросает мяч высоко в воздух, образуя угол 450 с направлением горизонтальной скорости передача мяча девушке, стоящей на расстоянии 10 м от нее. Какая скорость набирает мяч при броске?
Дано: θ = 450
Дальность полета мяча на броске R = 10 метров
Р=В2 без2θг
V=√Rg sin2θ
V=√10*9.8/Sin(2*60)
V=√98/Sin(120)
V=√98/0.86
V=√113.95
V=10.67 м/с
Следовательно, скорость мяча во время полета составляет 10.67 м / с.
Какая средняя скорость?
Ускоряющийся объект меняет направление скорости и скорости вместе с определенной продолжительностью времени.
Сумма всех скоростей, изменяющихся во времени, деленная на общее количество изменений, называется средней скоростью.
Большинство студентов впервые знакомятся с физикой в форме кинематики — области физики, которая изучает только движение объектов. Они используют уравнения для расчета скорости, положения и ускорения, чтобы научиться применять математику в реальном мире. Распространенный вопрос просит студентов вычислить конечную скорость объекта, не зная, как долго он ускоряется. Пока известно ускорение и смещение объекта, любой студент может решить эту проблему.
Анализ проблем
Убедитесь, что ускорение является постоянным. Постоянное ускорение будет простым числом, таким как 9, 8 метра в секунду в секунду (м / с ^ 2), и не будет изменяться в зависимости от времени или скорости.
Изучите задачу, чтобы найти смещение объекта и его начальную скорость.
Включите ускорение, смещение и начальную скорость в это уравнение: (Конечная скорость) ^ 2 = (Начальная скорость) ^ 2 + 2_ (Ускорение) _ (Смещение). Решите проблему, используя ручку, бумагу и калькулятор.
Пример проблемы
-
Простые алгебраические ошибки — самая распространенная ошибка, которую студенты делают в задачах кинематики.
Предположим, что автомобиль имеет начальную скорость 5 метров в секунду и разгоняется со скоростью 4 метра в секунду на расстоянии 10 метров. Вы можете узнать его конечную скорость и сколько времени машина проехала 10 метров.
Определите ускорение автомобиля. Здесь это четко указано как 4 м / с ^ 2. Это постоянное ускорение, потому что оно не меняется со временем; Ускорение автомобиля одинаково на протяжении всей проблемы.
Найти начальную скорость и смещение. Начальная скорость четко указана как 5 метров в секунду. Но проблема заключается только в пройденном расстоянии, а не в смещении. Используйте интуицию, чтобы утверждать, что пройденное расстояние и смещение одинаковы, 10 метров.
Решите уравнение (Конечная скорость) ^ 2 = (Начальная скорость) ^ 2 + 2_ (Ускорение) _ (Смещение). Включение значений дает V ^ 2 = 5 ^ 2 + 2_4_10. Взяв квадратный корень с обеих сторон (и снова используя интуицию, чтобы утверждать, что результат должен быть положительным), получаем V, равный квадратному корню из (25 + 80) = 10, 25 метра в секунду.
Решите за время после того, как конечная скорость найдена. Для этого вы можете изменить следующее уравнение: (Конечная скорость) = (Начальная скорость) + (Ускорение) * (Время). Поэтому в этом случае (Время) = (Конечная скорость — Начальная скорость) / (Ускорение). Время тогда равно (10, 25 — 5) / (4) = 1, 31 секунды.
подсказки
Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.
Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).
Рис.1. Так выглядит формула, по которой можно вычислить путь тела, не зная, сколько времени занимало движение
Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.
Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.
Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.
Выводим формулу пути без времени
Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.
В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону).
Сонаправленные или противоположно направленные векторы называют коллинеарными векторами. Прочитайте подробнее о коллинеарных векторах.
Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:
[ large begin{cases} S = v_{0} cdot t + displaystylefrac{a}{2} cdot t^{2} \ v = v_{0} + a cdot t end{cases} ]
( large v_{0} left( frac{text{м}}{c} right)) – начальная скорость тела;
( large v left( frac{text{м}}{c} right)) – конечная скорость;
( large a left( frac{text{м}}{c^{2}} right)) – ускорение тела;
( large S left( text{м} right)) – путь, пройденный телом;
(large t left( c right)) – время, за которое тело прошло этот путь.
В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.
Что сделать, чтобы получить формулу пути, в которой отсутствует время:
- сначала получить выражение для времени t из уравнения для скорости;
- затем в формулу пути подставить полученное выражение вместо времени t.
Выражаем время из формулы для скорости
Выпишем формулу, связывающую начальную и конечную скорость тела:
[ large v = v_{0} + a cdot t ]
Избавимся в правой части от начальной скорости, обозначенной символом ( v_{0}). Для этого из обеих частей уравнения вычтем число ( v_{0}). Получим такую запись:
[ large v — v_{0} = a cdot t ]
Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». Для этого разделим обе части уравнения на «a»:
[ large frac{ v — v_{0}}{a} = t ]
Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».
В формулу пути подставим выражение для времени
Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:
[ large begin{cases} S = v_{0}cdot t + displaystyle frac{a}{2}cdot t^{2}\ displaystyle frac{v — v_{0}}{a} = t end{cases} ]
В первом уравнении системы будем заменять символ t дробью из второго уравнения. Тогда система из двух уравнений превратится в единственное уравнение. И в этом уравнении не будет символа t времени:
[large S = v_{0} cdot frac{ v — v_{0}}{a} + frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]
Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.
Упрощаем выражение, расположенное до знака «плюс» в правой части
Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:
[large v_{0} cdot frac{ v — v_{0}}{a} ]
Умножим числитель дроби на число (v_{0}).
Для этого:
- сначала числитель обособим скобками;
- затем запишем число (v_{0}) перед скобками;
- а потом внесем это число внутрь скобок.
В числитель дроби, обособленный с помощью скобок помещаем число (v_{0}):
[large v_{0} cdot frac{ (v — v_{0})}{a} = frac{ v_{0} cdot (v — v_{0})}{a} ]
Теперь необходимо умножить скобку на число (v_{0}). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.
Рис. 2. Чтобы умножить скобку на число, нужно умножить каждое слагаемое в скобке на это число
Нужно к каждой скорости в скобках дописать число (v_{0}), умножая его на эти скорости. Получим такое выражение:
[large frac{ v_{0} cdot (v — v_{0})}{a} = frac{ (v_{0} cdot v — v_{0} cdot v_{0})}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} ]
То есть, вместо первоначальной записи, мы получили такую запись:
[large v_{0} cdot frac{ (v — v_{0})}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} ]
Возводим в квадрат дробь
После знака «плюс» в правой части уравнения располагается дробь, которую нужно возвести в квадрат. Обратим внимание на эту дробь:
[large left( frac{ v — v_{0}}{a} right)^{2}]
Правильно возвести дробь в степень поможет рисунок 3.
Рис. 3. Дробь возводим в степень, отдельно возводя в эту степень ее числитель и знаменатель
В результате возведения в квадрат дробь приобретет такой вид:
[large left( frac{ v — v_{0}}{a} right)^{2} = frac{ (v — v_{0})^{2}}{a^{2}}]
В числителе этой дроби находится выражение в скобках, которое нужно возвести в квадрат. И нам придется применить одну из формул сокращенного умножения. Запоминать формулы сокращенного умножения удобно в виде, приведенном на рисунке 4.
Рис. 4. Удобный для запоминания вид формул сокращенного умножения
Используем для этого формулу сокращенного умножения, которая содержит знак «минус». Она называется «Квадрат разности». Тогда числитель дроби превратится в такую запись:
[large ( v — v_{0})^{2} = (v^{2} + v^{2}_{0} — 2vv_{0})]
Теперь можем записать полученную дробь:
[large frac{ (v — v_{0})^{2}}{a^{2}} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}} ]
Упрощаем правую часть, записанную после знака «плюс»
Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:
[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]
Мы уже провели некоторые преобразования и можем теперь заменить дробь, возводимую в квадрат более подробной записью:
[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2} = frac{a}{2} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}}]
Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.
Итак, поменяем местами знаменатели дробей:
[large frac{a}{2} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}} = frac{a}{a^{2}} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2}]
Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:
[large frac{a}{a^{2}} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2} = frac{1}{a} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2}]
А перемножив числители и знаменатели двух дробей, получим такую запись:
[large frac{1}{a} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:
[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».
Теперь, осталось сложить две дроби в правой части – дробь, записанную до знака «плюс» с дробью, записанной после знака «плюс». А чтобы эти дроби можно было сложить, нужно будет привести их к общему знаменателю.
Приводим к общему знаменателю дроби в правой части уравнения
Вернемся еще раз к первоначальному уравнению:
[large S = v_{0} cdot frac{ v — v_{0}}{a} + frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]
Заменим правую часть этого уравнения выражениями, которые мы получили:
[large S = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} + frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Сравним знаменатели дробей.
Первая дробь обладает знаменателем «a», а вторая – «2a». Выберем число «2a» в качестве общего знаменателя обеих дробей.
Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:
[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot 1]
Примечания:
- Нам известно, что если какое-либо число умножить на единицу, то после умножения это число не изменится. Значит, если какое-либо выражение умножить на единицу, то полученное выражение останется равным самому себе. На единицу можно умножать все, что угодно – дроби, выражения в скобках и т. п.
- Математики часто применяют прием умножения на единицу. А после этого единицу записывают в виде некоторой дроби. При этом используют правило: Единица – это дробь, у которой числитель и знаменатель равны (одинаковые).
Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:
[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot 1 = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot frac{2}{2}]
Получим такую дробь:
[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot frac{2}{2} = frac{ 2(v_{0} cdot v – v^{2}_{0} )}{2a} ]
Поместим ее в выражение для пути:
[large S = frac{ 2(v_{0} cdot v – v^{2}_{0} )}{2a} + frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Дроби с одинаковыми знаменателями складываем
Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:
[large S = frac{ 2(v_{0} cdot v – v^{2}_{0} ) + (v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Раскроем скобки в числителе полученного выражения:
[large S = frac{ 2v_{0} v – 2v^{2}_{0} + v^{2} + v^{2}_{0} — 2vv_{0}}{2a}]
Примечание: Обратим внимание на то, что в числителе дважды встречается член (2v_{0} v), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа (2v_{0}v) вычитается такое же число (2vv_{0}). В конце концов, это число покидает нашу запись и, она упрощается:
[large S = frac{ – 2v^{2}_{0} + v^{2} + v^{2}_{0}}{2a}]
Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:
[large S = frac{ v^{2} + v^{2}_{0} – 2v^{2}_{0}}{2a}]
Вычтем подобные члены, содержащие ( v^{2}_{0}):
[large v^{2}_{0} – 2v^{2}_{0} = – v^{2}_{0} ]
В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:
[large boxed{ S = frac{ v^{2} — v^{2}_{0}}{2a} }]
Примечания:
- Это формула, с помощью которой можно рассчитать путь тела, когда известны его начальная и конечная скорость, а, так же, ускорение.
- Видно, что время t в правой части этого выражения отсутствует.
- Мы выводили эту формулу для случая, когда тело увеличивало скорость.
Как выглядит формула пути без времени, когда скорость тела уменьшается
Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:
[large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]
Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:
[ large begin{cases} S = v_{0} cdot t — displaystyle frac{a}{2} cdot t^{2} \ v = v_{0} — a cdot t end{cases} ]
Выводы
Пусть нам известны начальная и конечная скорость тела и его ускорение. Тогда путь, пройденный телом, можно рассчитать так:
- Когда движение равноускоренное и скорость тела увеличивается: [large boxed{ S = frac{ v^{2} — v^{2}_{0}}{2a} }]
- А когда движение равнозамедленное и скорость уменьшается: [large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]
Скорость, время и ускорение
Расчеты
Три этих физических величины взаимосвязаны между собой процессом движения. Если известны две из этих величин, можно найти третью.
Скорость тела при условии равноускоренного прямолинейного движения определяем по формуле:
V = V0 + а*t
V0 — начальная скорость (при t = 0);
а — ускорение;
t — время.
Итак, чтобы найти скорость, к начальной скорости прибавляем произведение ускорения на время.
Если V0 = 0, то V = а*t.
Чтобы найти время, нужно вначале найти разность между скоростью в данный момент и начальной скоростью, затем полученный результат разделить на ускорение.
t = (V — V0) / а
Ускорение показывает изменение скорости движущегося тела, рассчитывается по двум скоростям и времени. Чтобы вычислить ускорение, следует найти разницу между скоростью в данный момент и начальной скоростью, затем все это разделить на время.
При ускорении:
а = (V — V0) / t
При торможении:
а = (V0 — V) / t
Ускорение — величина векторная, которая задается не только числом, но и направлением, измеряется в метрах в секунду (м/с2).
Чтобы рассчитать среднее ускорение, находим разницу между начальной и конечной скоростями Δv, полученный результат делим на разницу между временем Δt.(начальным и конечным) :
а = Δv / Δt
Быстро и правильно рассчитать величину скорости, ускорения или найти время вам поможет онлайн калькулятор.
Расчет скорости, времени и ускорения
Движение тела без начальной скорости
Во многих случаях тело начинает движение из состояния покоя, то есть, из состояния с нулевой начальной скоростью. Поговорим кратко о движении тела без начальной скорости.
Начальная скорость тела в Системе Отсчета
Описание движения тела начинается с определения Системы Отсчета – то есть с определения тела отсчета, координатных осей и метода измерения времени.
Рис. 1. Система отсчета.
При этом возможны случаи, когда скорость тела в нулевой момент времени равна нулю. То есть, тело в начальный рассматриваемый момент времени не движется относительно тела отсчета (хотя, оно может двигаться в других системах).
Например, пассажир движущегося поезда некоторое время сидит на своем месте, а потом переходит на другое место. В Системе Отсчета, связанной с рельсами, он постоянно движется. Однако, в Системе Отсчета, связанной с вагоном, он в нулевой момент времени покоится, и лишь спустя некоторое время начинает движение.
Рис. 2. Поезд, пассажир, относительность движения.
Таким образом, начальная скорость тела зависит от выбранной Системы Отсчета.
Формулы кинематики для случая нулевой начальной скорости
Если начальная скорость тела равна нулю, а тело через некоторое время переместилось, значит, на тело действовала некоторая сила, которая привела к появлению ускорения, в результате которого и произошло перемещение тела. Иначе говоря, тело двигалось с ускорением. То есть, можно использовать общие формулы кинематики для равноускоренного движения:
$$overrightarrow x=overrightarrow x_0+overrightarrow v_0t+$$
$$overrightarrow v=overrightarrow v_0+overrightarrow at$$
Подставив в эти формулы $overrightarrow v_0 = 0$, получим:
$$overrightarrow v=overrightarrow at$$
Если построить графики этих формул и сравнить их с общими графиками, то можно отметить следующие особенности.
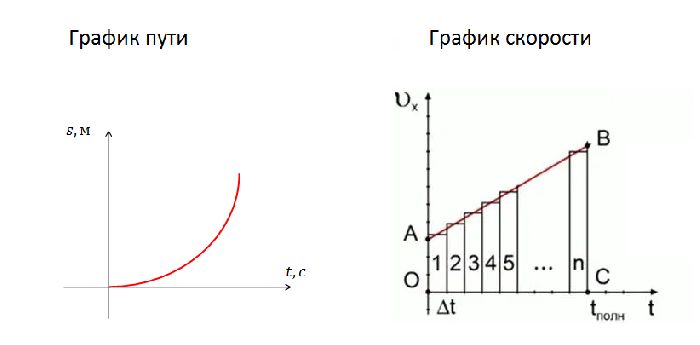
График пути представляет собой параболу, такую же, как при движении с начальной скоростью. Однако, эта парабола симметрична относительно оси ординат, и ее вершина пересекает эту ось. Следовательно, если тело двигалось с тем же ускорением до принятого в Системе Отсчета начального момента, то в этот момент перемещение тела имеет экстремальное (наибольшее или наименьшее) значение. Например, если рассматривается свободное падение тела, то нулевой момент будет соответствовать высшей точке траектории.
График скорости представляет собой прямую, имеющую тот же наклон, как и при движении с начальной скоростью, но, пересекающую начало координат.
Рис. 3. Графики пути и скорости для равноускоренного движения.
Выбор Системы Отсчета
Формулы, описывающие движение тела без начальной скорости, проще. Поэтому при решении задач следует, по возможности, выбирать Систему Отсчета так, чтобы у рассматриваемого тела начальная скорость была равна нулю.
Особенно простая форма получается, если и начальное перемещение тела также будет нулевым. Например, для описанного выше примера перехода пассажира с одного места на другое – Систему Отсчета разумно связать с креслом пассажира.
Что мы узнали?
Формулы кинематики для движения без начальной скорости проще. Поэтому следует по возможности выбирать Систему Отсчета так, чтобы рассматриваемые тела в этой системе не имели начальной скорости.
Как найти ускорение? Какова формула, по которой вычисляют ускорение?
Всё зависит от того, в каком разделе физики Вы находитесь. Точнее даже сказать: в каком разделе механики.
а) ускорение при равноускоренном прямолинейном движении.
Чтобы найти ускорение при равноускоренном прямолинейном движении, достаточно воспользоваться формулой
a = Δv/Δt
Δv — величина изменения скорости;
Δt — время (изменение времени).
или же формулой
a = (v – v0)/t
v — конечная скорость тела;
v0 — начальная скорость тела;
б) ускорение при движении по окружности.
Чтобы найти ускорение при движении по окружности, чаще всего применяется формула:
a = (v^2)/r
a — центростремительное ускорение;
v — линейная скорость тела;
r — радиус окружности.
Но есть и другие формулы:
a = 4 * (π^2) * r/(T^2)
a — центростремительное ускорение;
r — радиус окружности;
T — период обращения тела;
a = 4 * (π^2) * r * (ν^2)
a — центростремительное ускорение;
r — радиус окружности;
ν — частота обращения тела;
a = (ω^2) * r
a — центростремительное ускорение;
ω — угловая скорость тела;
r — радиус окружности.
В динамике ускорение находится по второму закону Ньютона.
Второй закон Ньютона звучит таким образом:
Формула 2-го закона Ньютона такова:
a = F/m
F — сила (величина силы);
Искать «а» ради «ускорения»-пустое занятие. Искать надо F-Силу,которая вызывает движение,и изменяет его. S/tt=F/m. S,t,m можно измерить. F=?
Ошибка Ньютон: S=att/2. S=att ! (без /2).
«а»-это ЭНЕРГИЯ движения. Она НЕ зависит от графика движения, и численно = S/tt (V/t).
У падающего «яблока..» несколько скоростей: нач. скорость, кон.скорость,средняя скорость, at, 2at. «средняя скорость»-(S/t)-это та-же скорость at,но выраженная через ЭНЕРГИЮ и ВРЕМЯ: F/m*t.
ВСЕ расчёты на движение надо делать ТОЛЬКО из СРЕДНЕЙ скорости! (Энергия одинакова, и НЕ зависит от графика движения). И нет «надобности» в «интегралах». . Задачка: машина m=1165 кг, прошла 250 м. за 18 с.(набрала скорость от 0 до 27,7 м/с за 18 сек.) («Жигули»). Вопрос: какая мощность мотора?
Всякий механизм имеет КПД. КПД ДВС (у бензиновых двс=16%).Решение: S/tt=F/m. 250/324=F/1165, (или 13,9/18=F/1165). F=900 кг.м/сс. Это 12 л.с. при 100% КПД ! При 16% мощность=75 л.с. (а,Да! «ускорение»? оно =0,77 м/сс. ). Но и без «а»не обойтись.
Грубая ошибка, находить «а»: Vo=0. V кон.=27,7. t=18 сек. а=(27,7-0)/18. а=1,5 м/сс. Мощность мотора=150 л.с.
То-же с «яблоком. » Vo=0, Vкон.=9,8. t=1 c. Правильно: (0+9,8)/2t. a=4,9 м/cc S=4,9 м.
«Если тело упало на Землю с высоты h, то S/tt ВСЕГДА . РАВНО числу 4,9. Это число 4,9 м/сс и ЕСТЬ «УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ»! Скорость: м/с. Ускорение-м/сек.сек. 9,8-это скорость,(но НЕ ускорение).
Сколько ошибок (и слёз) при решении задач:
Vo=5. t=10. a=2. S=? a=? V кон.=?
Решение: S=Vot+att. S=5/10+2*10*10. S=250. a=S/tt. a=2,5. V кон.=Vo+2at. Vкон.=5+2*2*10. V кон.=45. Проверка:S=att. 2,5*10*10=250. S=(v+V)/2*t. (5+45)/2*10. S=250 м.
По принятым формулам: S=(vo+att/2)*t. S=5*10+2*10/10/2=150 м. a=2S/tt. 300/100=3 м/сс
Скорость, время и ускорение
Три этих физических величины взаимосвязаны между собой процессом движения. Если известны две из этих величин, можно найти третью.
Скорость тела при условии равноускоренного прямолинейного движения определяем по формуле:
V = V0 + а*t
V0 — начальная скорость (при t = 0);
а — ускорение;
t — время.
Итак, чтобы найти скорость, к начальной скорости прибавляем произведение ускорения на время.
Если V0 = 0, то V = а*t.
Чтобы найти время, нужно вначале найти разность между скоростью в данный момент и начальной скоростью, затем полученный результат разделить на ускорение.
t = (V — V0) / а
Ускорение показывает изменение скорости движущегося тела, рассчитывается по двум скоростям и времени. Чтобы вычислить ускорение, следует найти разницу между скоростью в данный момент и начальной скоростью, затем все это разделить на время.
При ускорении:
а = (V — V0) / t
а = (V0 — V) / t
Ускорение — величина векторная, которая задается не только числом, но и направлением, измеряется в метрах в секунду (м/с2).
Чтобы рассчитать среднее ускорение, находим разницу между начальной и конечной скоростями Δ v, полученный результат делим на разницу между временем Δ t.(начальным и конечным) :
а = Δ v / Δ t
Быстро и правильно рассчитать величину скорости, ускорения или найти время вам поможет онлайн калькулятор.