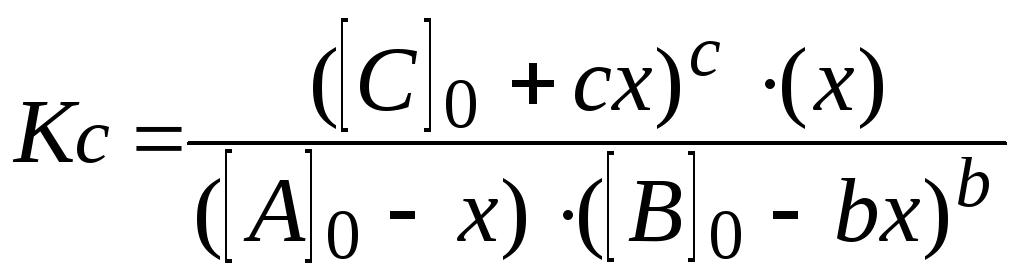Вычисление концентрации веществ, участвующих в реакции
Задача 18.
Реакция идет по уравнению: 4НСl + О2 = 2Н2О + 2Сl2. Через некоторое время после начала реакции концентрации участвующих в ней веществ стали (моль/л) НСl = 0,85; О2 = 0,44; Сl2 = 0,30. Какими были концентрации НСl и О2 в начале реакции?
Решение:
Для нахождения исходных концентраций НСl и О2 учтем, что, согласно уравнению реакции, из 4 молей НСl и 1 моля О2 образуется по 2 моля Н2О и Сl2. Поскольку по условию задачи в каждом литре системы образовалось по 0,3 моля, Н2О и Сl2,то при этом было израсходовано 0,6 молей НСl и 0,15 молей О2. Таким образом, искомые исходные концентрации равны:
[НСl]исх = 0,6 + 0,85 = 1,45 моль/л;
[О2]исх = 0,15 + 0,44 = 0,59 моль/л.
Задача 19.
Реакция идет по уравнению N2 + O2 = 2NO. Концентрации исходных веществ до начала реакции были [N2]исх = 0,049 моль/л, [O2] = 0,01моль/л. Вычислите концентрацию этих веществ в момент когда [NO] = 0,005 моль/л.
Решение:
[N2]исх = 0,049 моль/л
[O2]исх =0,01моль/л
[NO] = 0,005 моль/л
Уравнение реакции имеет вид:
N2 + O2 = 2NO
1моль 1моль 2моль
Из уравнения реакции вытекает, что количество продукта реакции NO превышает в 2 раза количество исходных веществ N2 и O2. Отсюда
n(N2) = n(O2) = 0,005/2 = 0,0025 моль/л.
c(N2) = 0,049 – 0,0025 = 0,0465 моль/л;
c(O2) = 0,01 – 0,0025 = 0,0075 моль/л.
Как определять исходную концентрацию вещества
Вещества, вступающие в химическую реакцию, претерпевают изменения состава и строения, превращаясь в продукты реакции. Концентрация исходных веществ уменьшается вплоть до нуля, если реакция идет до конца. Но может протекать обратная реакция, когда продукты распадаются на исходные вещества. В таком случае устанавливается равновесие, когда скорость прямой и обратной реакции становится одинаковой. Разумеется, равновесные концентрации веществ будут меньше исходных.

Инструкция
Произошла химическая реакция по схеме: А + 2Б = В. Исходные вещества и продукт реакции – газы. В какой-то момент установилось равновесие, то есть, скорость прямой реакции (А + 2Б = В) сравнялась со скоростью обратной (В = А + 2Б). Известно, что равновесная концентрация вещества А равна 0,12 моль/литр, элемента Б – 0,24 моль/литр, а вещества В – 0,432 моль/литр. Требуется определить исходные концентрации А и Б.
Изучите схему химического взаимодействия. Из нее следует, что один моль продукта (элемента В) образовывался из одного моля вещества А и двух молей вещества Б. Если в одном литре реакционного объема образовывалось 0,432 моля элемента В (по условиям задачи), то, соответственно, одновременно расходовалось 0,432 моля вещества А и 0,864 моля элемента Б.
Вам известны равновесные концентрации исходных веществ: [A] = 0,12 моль/литр, [Б] = 0,24 моль/литр. Прибавив к этим величинам те, которые были израсходованы в ходе реакции, вы получите величины исходных концентраций: [A]0 = 0,12 + 0,432 = 0,552 моль/литр; [Б]0 = 0,24 + 0,864 = 1,104 моль/литр.
Также вы можете определить исходные концентрации веществ с помощью константы равновесия (Кр) — отношения произведений равновесных концентраций продуктов реакции к произведению равновесных концентраций исходных веществ. Константа равновесия рассчитывается по формуле: Кр = [C]n [D]m /([A]0x[B]0y), где [C] и [D] – равновесные концентрации продуктов реакции С и D; n, m – их коэффициенты. Соответственно, [A]0, [В]0 – равновесные концентрации элементов, вступающих в реакцию; x,y – их коэффициенты.
Зная точную схему протекающей реакции, равновесную концентрацию хотя бы одного продукта и исходного вещества, а также величину константы равновесия, можно записать условия этой задачи в виде системы двух уравнений с двумя неизвестными.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Зная величины констант равновесия и используя стехиометрические соотношения реакции (закон сохранения массы), рассчитывают равновесный состав продуктов по следующей схеме.
Пишут уравнение реакции.
2. Пишут под формулами уравнения начальные концентрации исходных веществ (в моль/л). Если начальные концентрации продуктов реакции не оговариваются в условии задачи, они обычно принимаются равными нулю.
3. Принимают, что в ходе реакции до состояния равновесия прореагировало x моль/л какого-либо вещества. Обычно за x принимают изменение концентрации того реагента, стехиометрический коэффициент при котором в уравнении реакции наименьший, чтобы избежать дробных коэффициентов при неизвестном x. Например, прореагировало x моль/л вещества А.
4. По уравнению реакции определяют изменение концентраций других веществ.
5. Определяют равновесные концентрации веществ. При протекании реакции в прямом направлении до состояния равновесия происходит уменьшение концентраций исходных веществ и увеличение концентраций продуктов реакции.
по уравнению 1 b c 1
6. Пишут выражение закона действующих масс. Подставляют в него найденные значения равновесных концентраций.
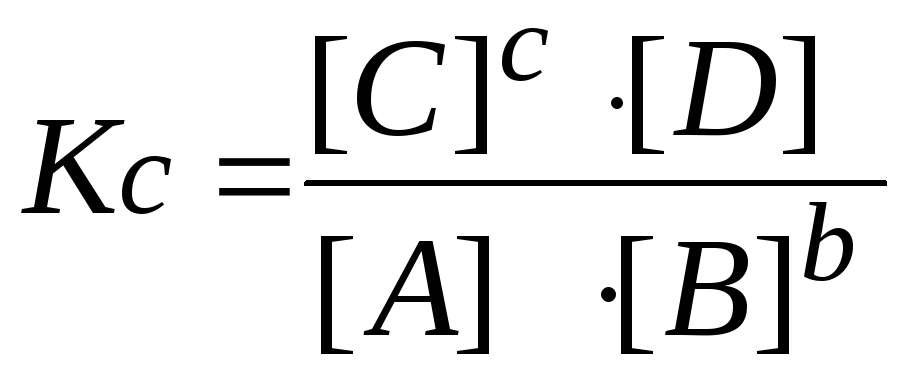
7. Решают уравнение. При этом учитывают, что отрицательный корень не имеет физического смысла, и убыль концентрации исходного вещества не может быть больше величины самой концентрации (начальная концентрация исходного вещества не может быть меньше его остаточной равновесной концентрации).
Находят равновесные концентрации.
4. Смещение химического равновесия. Принцип Ле Шателье
Истинное химическое равновесие является динамическим и подвижным: изменение внешних условий (температуры, давления, концентраций реагирующих веществ) ведет к смещению равновесия в сторону прямой или обратной реакции.
Характер влияния внешних факторов на равновесные системы выражает принцип Ле Шателье.
Если на систему, находящуюся в состоянии равновесия, оказать внешнее воздействие, то смещение равновесия происходит в сторону той реакции (прямой или обратной), которая ослабляет эффект внешнего воздействия.
4.1. Изменение концентраций
Равновесное состояние в системе
характеризуется (для одной и той же температуры) константой равновесия:
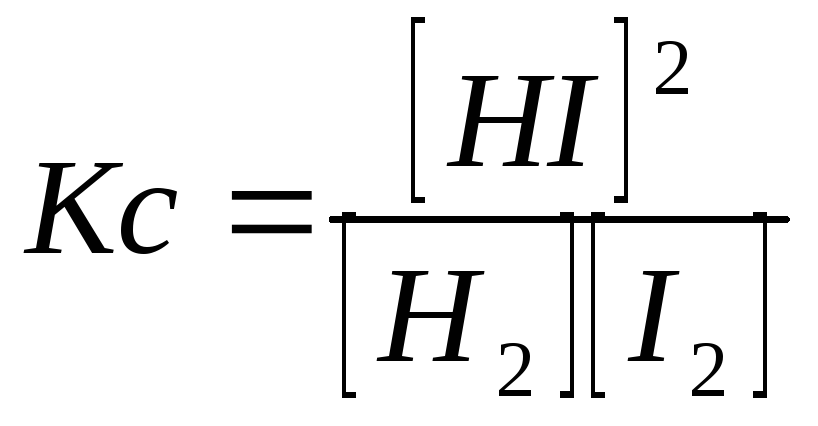
Если, например, в систему добавить водород, т.е. увеличить его концентрацию, то скорость прямой реакции увеличится (в соответствии с законом действующих масс):
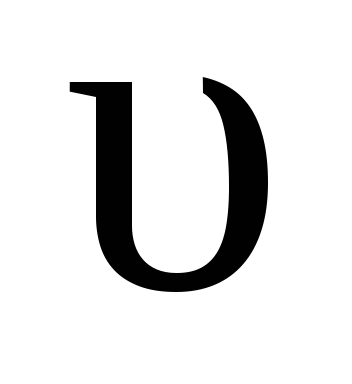

равновесие сместится вправо. Концентрация йодоводорода будет увеличиваться, а концентрация водорода и йода будет уменьшаться. Процесс будет протекать до тех пор, пока не установится новое равновесие. Новые равновесные концентрации всех компонентов будут другими, но соотношение между ними, определяемое константой равновесия, останется постоянным.
Если в систему ввести дополнительное количество йодоводорода, то скорость обратной реакции увеличится:
равновесие сместится влево.
В соответствии с принципом Ле Шателье:
— при увеличении концентрации какого-либо из веществ, участвующих в равновесии, равновесие смещается в сторону расхода этого вещества;
— при уменьшении концентрации какого-либо из веществ равновесие смещается в сторону образования этого вещества.
Удаление из системы продуктов (или продукта) реакции ведет к смещению равновесия в сторону прямой реакции, а уменьшение концентрации исходных (или исходного) веществ, приводит к сдвигу равновесия в направлении обратной реакции.
Задачник по общей и неорганической химии
5. Химическое равновесие
5.1. Состояние химического равновесия
Теоретическая часть
характеризуется наступлением состояния истинного химического равновесия. В этом состоянии выполняется (по определению) условие неизменности во времени молярных концентраций реагентов и продуктов, называемых равновесными концентрациями.
В отличие от молярной концентрации некоторого вещества В (сВ) в любом неравновесном состоянии системы равновесная концентрация того же вещества обозначается квадратными скобками [В].
Для обратимой химической реакции, протекающей при некоторой температуре, устанавливаются любые, но постоянные равновесные концентрации [А], [В], [С], [D]. Они не зависят друг от друга, а определяются только положением состояния равновесия.
В соответствии с законом действующих масс состояние равновесной химической системы характеризуется константой равновесия:

Выражение (5.2) позволяет рассчитать KС по известным равновесным концентрациям всех веществ гомогенной газофазной реакции (5.1), а также для гомогенной реакции в растворе, например
или концентрацию одного из веществ по известным равновесным концентрациям остальных веществ и KС.
Пример 1. При некоторой температуре в системе
равновесные концентрации веществ равны соответственно 0,04, 0,12 и 0,06 моль/л. Рассчитать KС реакции.
Ответ. Для данной реакции KС = 0,54.
Если по условию задачи известна равновесная концентрация только одного продукта из нескольких, то перед расчетом KС необходимо вычислить незаданные равновесные концентрации продуктов по выражению
Пример 2. При некоторой температуре в системе
равновесные концентрации С2Н6, О2 и СО2 составили соответственно 0,22, 1,34 и 0,57 моль/л. Рассчитать KС реакции.
Ответ. Для данной реакции KС = 0,11.
Для гетерогенных реакций, в которых при данной температуре среди реагентов и продуктов присутствуют (помимо газов) отдельные фазы твердых и жидких веществ, равновесные концентрации твердых и жидких веществ в выражение для константы равновесия не входят ввиду их постоянства во всей области существования данных агрегатных состояний этих веществ.
Действительно, равновесная концентрация некоторого жидкого вещества В или твердого вещества С есть отношение их плотности (ρВ или ρС) к молярной массе (МВ или МС):
поэтому концентрации В(ж) и С(т) постоянны и не зависят от присутствующего количества этих веществ в реакции.
Для некоторой гетерогенной обратимой реакции
выражение для константы равновесия имеет вид
Состояние истинного равновесия в химической системе (5.1) называют также динамическим, поскольку в ней протекает двусторонняя реакция в прямом направлении (А и В — реагенты, С и D — продукты) и обратном (А и В — продукты, С и D — реагенты). Кроме того, подход к состоянию равновесия при некоторой температуре может осуществляться как в прямом, так и в обратном направлении (рис. 5.1, поля 1 и 2). При этом кривые зависимости соотношения неравновесных концентраций веществ (составлено аналогично выражению 5.2) от времени сходятся в точке, отвечающей (по оси абсцисс) значению KС для данной реакции.
В реакции (5.1), протекающей в прямом направлении, значения [С] и [D] будут максимальными концентрациями продуктов, а [A] и [В] минимальными остаточными концентрациями реагентов. Следовательно, KС фактически определяет равновесный (максимально возможный в данных условиях) выход каждого продукта.
Равновесный выход продукта отношение количества продукта в состоянии равновесия обратимой реакции (nравн) к стехиометрическому количеству этого продукта в той же, но необратимой реакции (nстех) или отношение соответствующих концентраций. Так, для реакции (5.1) имеем:
Если значение KС велико, то произведение [С] с x [D] d много больше произведения [A] a x [B] b , т. е. в системе преобладает прямое направление реакции и равновесные концентрации продуктов намного больше, чем равновесные концентрации реагентов, а потому выход продуктов С и D велик.
Аналогично при очень малом значении KС преобладает обратное направление реакции и выход продуктов С и D прямой реакции незначителен.
При KС = 1 преобладание прямого и обратного направления реакции отсутствует.
Если сложная химическая реакция осуществляется в два или большее число этапов, для которых известны значения KС, то константу равновесия этого процесса можно выразить через KС этапов, например (все вещества — газы):
В расчетных задачах этого раздела предполагается, что подход к состоянию равновесия обратимой реакции осуществляется за счет ее прямого направления. В начальный момент реакции, протекающей по реакции (5.1), концентрации газообразных реагентов имеют некоторые (любые заданные) значения с0А и с0В, а концентрации газообразных продуктов равны нулю (с0С = с0D = 0).
Если в реакции участвуют жидкие и твердые вещества, то считается, что они полностью нелетучи и потому не имеют никакой концентрации в газовой фазе.
При протекании реакции в прямом направлении до состояния равновесия происходит уменьшение концентраций газообразных реагентов и увеличение концентраций газообразных продуктов, определяемые по закону сохранения выражениями:
Эти выражения позволяют рассчитать равновесные концентрации веществ по начальным концентрациям реагентов при известном значении KС (и наоборот).
Пример 3. При некоторой температуре в системе
равновесная концентрация О2 составила 0,2 моль/л. Определите начальную концентрацию реагента.
Ответ. Начальная концентрация NO2 была равна 0,45 моль л.
Выражение для [NO2] выведено и подставлено в расчетную формулу из закона действующих масс (5.2):
Пример 4. При Т = const рассчитайте равновесные концентрации газообразных веществ в системе
если начальная концентрация СО составляла 0,16 моль л.

Ответ. Равновесные концентрации СO и СO2 равны соответственно 0,1 и 0,06 моль л.
Указанную систему уравнений можно было решить и относительно [СO2], а затем вычислить значение [СO]:
Пример 5. При Т = const рассчитайте равновесные концентрации реагента и продуктов в системе
если начальное количество PCl5 было 6 моль, а объем реактора составляет 5 л.
отсюда
Решая квадратное уравнение, получаем: [Cl2]1 = + 0,2 моль/л (реальный корень); [Cl2]2 = 0,24 моль/л (нереальный корень);
Ответ. Равновесные концентрации Cl2, PCl5 и PCl3 составляют 0,2, 1,0 и 0,2 моль л соответственно.
Обратите внимание на то, что один из корней квадратного уравнения всегда будет нереальным, т.е. его значение будет либо отрицательным (а такие значения концентраций не имеют химического смысла), либо положительным, но дающим для реагента неравенство [ ] > с (а начальная концентрация реагента, по определению, не может быть меньше его остаточной равновесной концентрации). В этом примере значение нереального корня отрицательное.
В системе A(г)+2В(г)С(г) равновесие концентрации равны:
[A]=0,6 моль/л, [В]=1,2 моль/л, [С]=2,16 моль/л.
Найдите константу равновесия реакции и исходные концентрации веществ А и В.
Из уравнения видны, что 1 моль вещества А образует 1 моль вещества С, значит 2,16 моля образуется на 2,16 моль А.
4.3.6. Расчеты массы (объема, количества вещества) продукта реакции, если одно из веществ дано в виде раствора с определенной массовой долей растворенного вещества.
Для расчета массы (объема, количества вещества) продукта реакции, если данные по одному из веществ представлены в виде раствора с определенной массовой долей этого растворенного вещества, следует воспользоваться нижеследующим алгоритмом:
1) Прежде всего следует найти массу растворенного вещества. Возможны две ситуации:
* В условии даны масса раствора и массовая доля растворенного вещества (концентрация). В этом случае масса растворенного вещества рассчитывается по формуле:
* В условии даны объем раствора вещества, плотность этого раствора и массовая доля растворенного вещества в этом растворе. В таком случае следует воспользоваться формулой для расчета массы раствора:
После чего следует рассчитать массу растворенного вещества по формуле 1.
2) Рассчитать количество вещества (моль) участника реакции, масса которого стала известна из расчетов выше. Для этого воспользоваться формулой:
3) Записать уравнение реакции и убедиться в правильности расставленных коэффициентов.
4) Рассчитать количество моль интересующего участника реакции исходя из известного количества другого участника реакции, зная, что количества веществ любых двух участников реакции A и B относятся друг к другу как коэффициенты перед этими же веществами в уравнении реакции, то есть:
Если в условии требовалось рассчитать количество вещества, то действия на этом заканчиваются. Если же требуется найти его массу или объем, следует переходить к следующему пункту.
5) Зная количество вещества, определенное в п.4, мы можем рассчитать его массу по формуле:
Также, если вещество является газообразным и речь идет о нормальных условиях (н.у.), его объем может быть рассчитан по формуле:
Рассмотрим пару примеров расчетных задач по этой теме.
Пример 1
Рассчитайте массу осадка, который образуется при добавлении к 147 г 20%-ного раствора серной кислоты избытка раствора нитрата бария.
Решение:
1) Рассчитаем массу чистой серной кислоты:
m(H2SO4) = w(H2SO4) ∙ m(р-ра H2SO4)/100% = 147 г ∙ 20% /100% = 29,4 г
2) Рассчитаем количество вещества (моль) серной кислоты:
n(H2SO4) = m(H2SO4) / M(H2SO4) = 29,4 г/98 г/моль = 0,3 моль.
3) Запишем уравнение взаимодействия серной кислоты с нитратом бария:
H2SO4 + Ba(NO3)2 = BaSO4↓ + 2HNO3
4) В результате расчетов стало известно количество вещества серной кислоты. Осадок представляет собой сульфат бария. Зная, что:
n(BaSO4)/n(H2SO4) = k(BaSO4)/k(H2SO4), где n — количество вещества, а k — коэффициент в уравнении реакции,
можем записать:
n(BaSO4) = n(H2SO4) ∙ k(H2SO4)/k(BaSO4) = 0,3 моль ∙ 1/1 = 0,3 моль
5) Тогда масса осадка, т.е. сульфата бария, может быть рассчитана следующим образом:
m(BaSO4) = M(BaSO4) ∙ n(BaSO4) = 233 г/моль ∙ 0,3 моль = 69,9 г
Пример 2
Какой объем газа (н.у.) выделится при растворении необходимого количества сульфида железа (II) в 20%-ном растворе соляной кислоты с плотностью 1,1 г/мл и объемом 83 мл.
Решение:
1) Рассчитаем массу раствора соляной кислоты:
m(р-ра HCl) = V(р-ра HCl) ∙ ρ(р-ра HCl) = 83 мл ∙ 1,1 г/мл = 91,3 г
Далее рассчитаем массу чистого хлороводорода, входящего в состав кислоты:
m(HCl) = m(р-ра HCl) ∙ w(HCl)/100% = 91,3 г ∙ 20%/100% = 18,26 г
2) Рассчитаем количество вещества хлороводорода:
n(HCl) = m(HCl)/M(HCl) = 18,26 г/36,5 г/моль = 0,5 моль;
3) Запишем уравнение реакции сульфида железа (II) с соляной кислотой:
FeS + 2HCl = FeCl2 + H2S↑
4) Исходя из уравнения реакции следует, что количество прореагировавшей соляной кислоты с количеством выделившегося сероводорода связано соотношением:
n(HCl)/n(H2S) = 2/1, где 2 и 1 — коэффициенты перед HCl и и H2S соответственно
Следовательно:
n(H2S) = n(HCl)/2 = 0,5/2 = 0,25 моль
5) Объем любого газа, находящегося при нормальных условиях, можно рассчитать по формуле V(газа) = Vm ∙ n(газа), тогда:
V(H2S) = Vm ∙ n(H2S) = 22,4 л/моль ∙ 0,25 моль = 5,6 л
Задачи
Рассчитать концентрацию в этот момент и начальную скорость прямой реакции.
Константа скорости гомогенной реакции
равна . Через некоторое время от начала реакции в реакционной смеси обнаружено 20 % от первоначального количества HJ, 0,2 моль/л
и 0,4 моль/л
. Рассчитать концентрацию
в этот момент и начальную скорость прямой реакции.
Решение. Известна концентрация одного из продуктов реакции – , что позволяет вычислить изменение концентрации
к моменту времени
:
моль/л;
моль/л.
Тогда, пользуясь соотношением (15)
,
определяем:
(моль/л);
(моль/л);
(моль/л).
Искомая концентрация в момент времени
:
моль/л;
Находим начальные концентрации реагентов.
Поскольку , то
моль/л.
О втором реагенте () известно, что в реакционной смеси обнаружено (
) 20 % от первоначального количества; значит, прореагировало (
) 80 %. Составляем пропорцию:
С0(HI) – 100%
Δc(HI) = 0,4 моль/л – 80%
откуда
(моль/л).
Начальную скорость прямой реакции рассчитываем по закону действующих масс:
.
Результаты расчетов представим в виде таблицы 6.
Таблица 6
| 2 | 1 | 1 | 2 | |
| 0,5 | 0,4 | 0 | 0 | |
| 0,4 | 0,2 | 0,2 | 0,4 | |
| 0,1 | 0,2 | 0,2 | 0,4 | |
| 0,2 |