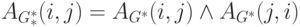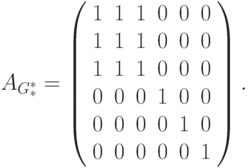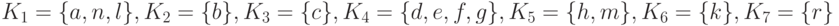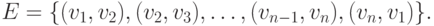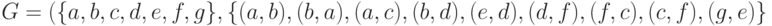Как найти компоненты сильной связности графа - Avtoru.top

Поиск компонент сильной связности: алгоритм Косарайю

Время на прочтение
2 мин

Количество просмотров 33K

На хабре нет ни одной статьи о поиске компонент сильной связности. Однако это интересная задача, имеющая приложения в самых разных сферах: системах рекомендаций, математической логике и, неожиданно, экологии. Ниже формулировка задачи и решение — алгоритм Косарайю.

К делу:

Заметим: отношение сильной связности — это отношение эквивалентности.

Компонентой сильной связности называется класс эквивалентности множества вершин ориентированного графа относительно отношения сильной связности. Другими словами компонента сильной связности = сильно связный подграф. Так как сильная связность — это отношение эквивалентности, то граф разбивается на сильно связные компоненты. Наша задача найти все такие классы эквивалентности.

Алгоритм Косарайю

Инвертированием ориентированного графа назовем процедуру, в ходе которой поменяем направление каждого ребра на противоположное.

Метод Косарайю прост для реализации и понимания. Так как компоненты сильной связности есть циклы, то они совпадают и у исходного графа и у его инвертирования.

Пусть дан ориентированный граф G = (V, E). Через G’ = (V, E’) обозначим интертирование G.

Будем обходить граф G в глубину, пока не посетим все вершины. Заведем массив out = [0…|V|-1] — время выхода из вершины. Под временем понимаются логические часы: изначально время равно 0, при переходе в вершину или выходе из неё время увеличивается на 1.

Когда обход закончится, заведем массив vertices, куда добавим все вершины в порядке увеличения времени выхода. Теперь запустим обход в глубинку на инвертированном графе G’. Каждый раз для обхода будем выбирать ещё не посещенную вершину с максимальным индексом в массиве vertices. Все вершины, посещенные в ходе одной итерации dfs, образуют компоненту сильной связности.

Время работы

Заметим: если граф представлен графом смежности, то нам не требуетcя хранить в памяти инвертированный граф. Иначе нам потребуется O(V+E) доп. памяти. Но, в любом случае, нам требуется O(V) памяти для массивов out и vertices.

Алгоритм состоит из двух обходов DFS. Каждый работает пропорционально V+E для разреженных графов и V^2 для насыщенных. Кроме того, нам требуется O(VlogV) для сортировки вершин при построении массива vertices.

Дополнительно

Корректность алгоритма и псевдокод можно посмотреть тут: www.jeffreykarres.com/blog/kosaraju

В начале статьи я упоминал приложения.

На SO писали про использование этого алгоритма для формальной верификации:
stackoverflow.com/questions/11212676/what-are-strongly-connected-components-used-for
А про экологию можно почитать в статье:
www.nceas.ucsb.edu/~allesina/PDF/Allesina2005.pdf

Источник

Содержание

1 Алгоритм
2 Доказательство корректности алгоритма
3 Время работы алгоритма
4 Псевдокод
5 Источники информации

Алгоритм

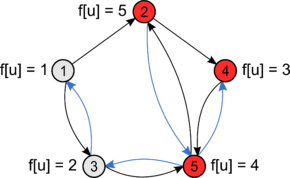
Вершины 2, 4, 5 сильносвязаны.
Синим цветом обозначен обод DFS по инвертированным ребрам

Компоненты сильной связности в графе можно найти с помощью поиска в глубину в 3 этапа:

Построить граф с обратными (инвертированными) рёбрами
Выполнить в поиск в глубину и найти — время окончания обработки вершины
Выполнить поиск в глубину в , перебирая вершины во внешнем цикле в порядке убывания

Полученные на 3-ем этапе деревья поиска в глубину будут являться компонентами сильной связности графа .
Так как компоненты сильной связности и графа совпадают, то первый поиск в глубину для нахождения можно выполнить на графе , а второй — на .

Доказательство корректности алгоритма

Теорема:

Вершины и взаимно достижимы после выполнения алгоритма они принадлежат одному дереву обхода в глубину.

Доказательство:

Если вершины и были взаимно достижимы в графе , то на третьем этапе будет найден путь из одной вершины в другую, это означает, что по окончанию алгоритма обе вершины лежат в одном поддереве.

Вершины и лежат в одном и том же дереве поиска в глубину на третьем этапе алгоритма. Значит, что они обе достижимы из корня этого дерева.
Вершина была рассмотрена вторым обходом в глубину раньше, чем и , значит время выхода из нее при первом обходе в глубину больше, чем время выхода из вершин и . Из этого мы получаем 2 случая:
1. Обе эти вершины были достижимы из в инвертированном графе. А это означает взаимную достижимость вершин и и взаимную достижимость вершин и . А складывая пути мы получаем взаимную достижимость вершин и .
2. Хотя бы одна не достижима из в инвертированном графе, например . Значит и была не достижима из в инвертированном графе, так как время выхода — больше . Значит между этими вершинами нет пути, но последнего быть не может, потому что была достижима из по пункту 1).

Значит, из случая 2.1 и не существования случая 2.2 получаем, что вершины и взаимно достижимы в обоих графах.

Время работы алгоритма

Для того, чтобы инвертировать все ребра в графе, представленном в виде списка потребуется действий. Для матричного представления графа не нужно выполнять никакие действия для его инвертирования.
Количество ребер в инвертированном равно количеству ребер в изначальном графе, поэтому поиск в глубину будет работать за
Поиск в глубину в исходном графе выполняется за .

В итоге получаем, что время работы алгоритма .

Псевдокод

Пусть — исходный граф, —инвертированный граф. В массиве будем хранить номера вершин в порядке окончания обработки поиском в глубину в графе . В результате получаем массив , который каждой вершине сопоставляет номер её компоненты.

   function dfs1(v):                                          
       color[v] = 1
       for (v, u) in E
           if not visited[u]
               dfs1(G[v][u])
       Добавляем вершину v в конец списка ord
   
   function dfs2(v):                                          
       component[v] = col
       for (v, u) in E
           if (вершина u еще не находится ни в какой компоненте)                       
               dfs2(H[v][u])
   
   function main():
       считываем исходные данные, формируем массивы G и H
       for u in V                           
           if not visited[u]
               dfs1(u)
       col = 1
       for (по всем вершинам u списка ord[] в обратном порядке)                                                        
           if (вершина u не находится ни в какой компоненте)
               dfs2(u)
               col++

Источники информации

Р.Седжвик. «Фундаментальные алгоритмы на С++. Алгоритмы на графах» — СПб, ДиаСофтЮП, 2002
MAXimal :: algo :: Поиск компонент сильной связности, построение конденсации графа
Визуализация поиска компонент сильной связности

Источник

С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.

Cоставляем матрицу смежности A(D) размерности (N− количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк – индексы вершин, из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят (если есть дуга, исходящая из вершины Vi и входящая в Vj, то элемент матрицы смежности, стоящий на пересечении I-той строки и J-того столбца равен 1, иначе – 0.).

Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) ориентированного графа по первой формуле утверждения 3, затем находим матрицу сильной связности S(D) ориентированного графа (она должна быть симметрической) по второй формуле из того же утверждения.

Алгоритм выделения компонент сильной связности

1. Присваиваем P=1 (P − количество компонент связности), .

2. Включаем в множество вершин Vp Компоненты сильной связности Dp вершины, соответствующие единицам первой строки матрицы Sp. В качестве матрицы A(Dp) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.

3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то P— количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как Sp+1, присваиваем P=P+1 и переходим к п. 2.

Пример

Выделим компоненты связности ориентированного графа, изображенного на рис. 6. В данной задаче количество вершин N=5.

Рис. 6.

Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом

Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:

, ,

Следовательно,

Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:

Присваиваем P=1 и составляем множество вершин первой компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины .

Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине V1, чтобы получить матрицу S2(D):

Присваиваем P=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S2(D), то есть . Составляем матрицу смежности для компоненты сильной связности исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:

Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2 ,чтобы получить матрицу S3(D), которая состоит из одного элемента:

И присваиваем P=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины .

Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:

< Предыдущая		Следующая >

Источник

Алгоритм определения компонент сильной связности орграфа

Удалить
из графа вершины источники, тупиковые
и изолированные вершины, зафиксировав
их как отдельные сильные компоненты.
Выбрать
некоторую вершину x_i.
Определить
для x_i.
Выполнить
операцию пересечения
и зафиксировать множество вершин,
вошедших в.
Удалить
из графа вершины, принадлежащие
и инцидентные им дуги. Если получен
подграфG’, то перейти
к п. 2. Если граф пуст, то перейти к п. 6.
Сформировать
множество классов C.

Для
определения
получим степенистроки x_iматрицы смежности A,
а для определениястепенистолбца x_i. Максимальный показатель степениn–1, так как учитываются
только кратчайшие маршруты. Затем
объединим полученные строки (степенистроки x_i)
со строкой, имеющей единственную 1 в
позиции вершиныx_i,
а полученные столбцы (степенистолбца
x_i)
объединим со столбцом, имеющим единственную
1 в позиции вершиныx_i.

определяется как множество вершин,
имеющих 1 в полученной матрице строке.определяется как множество вершин,
имеющих 1 в полученной матрице столбце.

Пример.Дан граф рис. 22.1.

Найти
компоненты сильной связности графа.

Анализируя
граф, находим, что вершина 5 тупиковая.
Удалив ее, обнаруживаем, что появилась
новая тупиковая вершина 4.

После
удаления вершины 4 получаем граф на трех
вершинах, для которого матрица смежности
равна

Рисунок
22.1

A=.

Выберем
вершину 1.

Для
этой вершины
=
– первая строка матрицы смежности.

Для
получения
возводим строку вершины 1 матрицыAво вторую степень, т.е. умножаем строку
вершины 1на матрицуA

=*=
.

Поскольку
после удаления вершин 4 и 5 в графе
осталось только три вершины, то вторая
степень – это предел.

Объединим
,со
строкой
,
представляющей вершину 1.

Получаем

=
{1}
=
=
.

В другом
представлении =
{1, 2, 3}.

Теперь
определим
.

=.=*=. {1}
=.

= {1}==.

В другом
представлении
=
{1, 2, 3}.

Таким
образом

=
{1, 2, 3} и= {1, 2, 3}.

Следовательно,

=
{1, 2, 3}{1,
2, 3} = {1, 2, 3}.

Так как
ранее были исключены тупиковые вершины
5 и 4, каждая из которых образует свой
класс сильной связности, то все классы
сильной связности будут такими {1, 2, 3},
{4}, {5}.

22.2.3 Определение компонент связности

Если
для любой вершины x_iвыполняется условие

то граф
сильно связен.

Поскольку
связный неорграф всегда сильно связен,
то полученный алгоритм определения
компонент сильной связности пригоден
и для определения компонент связности
неорграфов: Каждая компонента неорграфа
сильно связана, а между компонентами
связи нет.

Связность
орграфа проверяется удалением ориентации
дуг и установлением связности полученного
неорграфа.

Пример.
Дан граф рис. 22.2, для которого имеем

A=
.

Рисунок
22.2

В графе
изолированных вершин нет, поэтому
исключать ничего не надо.

Выберем
вершину 1.

В графе
6 вершин, поэтому для определения
инужно
возводить первую строку и первый столбец
матрицы смежности в степени с первой
по пятую.

Возводим
в степень первую строку матрицы A(сложение и умножение элементов булевские)

Первая
строка матрицы смежности

Вторая
степень первой строки матрицы смежности

=*
=.

Третья
степень первой строки матрицы смежности

=*
=.

При
возведении в третью степень получено
повторение строки, возводимой в степень,
поэтому операцию возведения в степень
прекращаем.

Если
продолжить возведение в степень, то
результат будет повторяться.

Найдем
.

= {1}=

=
=.

В других
обозначениях

= {1, 3, 5}.

Определим
.

=
.=
*
=
.

=
*
=
.

Результат
совпадает с начальным значением,
следовательно, возведение в степень
надо прекратить.

Найдем

=
{1}==
.

В других
обозначениях

=
{1, 3, 5}.

=
{1, 3, 5}{1,
3, 5} = {1, 3, 5}.

Вершины
1, 3, 5 принадлежат отдельной компоненте
связности, поэтому на дальнейший процесс
поиска других компонент связности
влиять не будут. для
уменьшения объема вычислений эти
вершины, вместе с инцидентными им
ребрами, можно исключить. Рассматриваемый
пример достаточно простой, поэтому
исключать ничего не будем.

Возьмем
вершину, не принадлежащую
,
например, 4.

Действуя
аналогично, находим

=*
=.

Получено
повторение строки, возводимой в степень,
поэтому операцию возведения прекращаем.

Найдем
.

=
{4}=

==.

В других
обозначениях

= {2, 4, 6}.

Определим
.

=
.=
*
=
.

=
*
=
.

Результат
совпадает с начальным значением,
следовательно, возведение в степень
надо прекратить.

Найдем

=
{4}==
.

В других
обозначениях

=
{2, 4, 6}.

=
{2, 4, 6}{2,
4, 6} = {2, 4, 6}.

Таким
образом, все вершины графа вошли в два
класса – в две компоненты связности C₁= {1, 3, 5} иC₄= {2,
4, 6}.

Соседние файлы в папке 3 — Графы

Источник

Взаимная достижимость, компоненты сильной связности и базы графа

По аналогии с графом достижимости определим граф сильной достижимости.

Определение 9.10. Пусть G=(V,E) — ориентированный граф. Граф сильной достижимости G_*^*=(V,E_*^*) для G имеет то же множество вершин V
и следующее множество ребер E_*^* ={ (u, v) | в графе G вершины v и u взаимно достижимы}.

По матрице графа достижимости 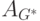$A_{G^*}$ легко построить матрицу $A_{G_*^*}$ графа
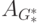
сильной достижимости.
Действительно из определений достижимости и сильной достижимости непосредственно
следует, то для всех пар (i,j), 1<= i,j <= n, значение элемента 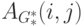$A_{G_*^*}(i,j)$ равно 1 тогда и только тогда,
когда оба элемента A_G*(i, j) и A_G*(j, i) равны 1, т.е.

$A_{G_*^*}(i,j) = A_{G^*}(i, j) wedge A_{G^*}( j, i)$

По матрице 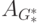$A_{G_*^*}$ можно выделить компоненты сильной связности графа G следующим образом.

Поместим в компоненту K₁ вершину v₁ и все такие вершины v_j, что A_{G_*^*}(1,j) = 1.
Пусть уже построены компоненты K₁, …, K_i и v_k — это вершина с минимальным номером, еще не попавшая в компоненты. Тогда поместим в компоненту K_{i+1} вершину v_k и все такие вершины v_j,
что A_{G_*^*}(k,j) = 1.

Повторяем шаг (2) до тех пор, пока все вершины не будут распределены по компонентам.

В нашем примере для графа G на рис.2 по матрице 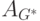$A_{G^*}$ получаем
следующую матрицу графа сильной достижимости

$A_{G_*^*}= left( begin{array}{cccccc} 1 & 1 & 1 & 0& 0& 0\ 1 & 1 & 1 & 0& 0& 0\ 1 &1 & 1 & 0& 0& 0\ 0 & 0 & 0 & 1& 0& 0\ 0 & 0 & 0 & 0& 1& 0\ 0 & 0 & 0 & 0& 0& 1 end{array}right).$

Используя описанную выше процедуру, находим, что вершины графа G разбиваются на 4 компоненты сильной связности: K₁= {v₁, v₂, v₃}, K₂ ={ v₄}, K₃ ={ v₅}, K₄ ={ v₆}.

На множестве компонент сильной связности также определим отношение достижимости.

Определение 9.11. Пусть K и K’ — компоненты сильной связности графа G.
Компонента K достижима из компоненты K^prime, если K= K’
или существуют такие две вершины u in K
и v in K' , что u достижима из v. K строго достижима из K^prime, если Kne K' и K достижима из K’.

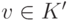
Компонента K называется минимальной, если она не является строго
достижимой ни из какой компоненты.

Так как все вершины в одной компоненте взаимно достижимы, то нетрудно понять,
что отношения достижимости и строгой достижимости на компонентах не зависят
от выбора вершин 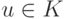u in K и v in K' .

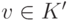
Из определения легко выводится следующая характеристика строгой достижимости.

Лемма 9.3.
Отношение строгой достижимости является отношением частичного порядка, т.е. оно
антирефлексивно, антисимметрично и транзитивно.

Это отношение можно представлять в виде ориентированного графа, вершинам и которого
являются компоненты, а ребро (K’, K) означает, что K строго достижима из K’.
На рис. 9.4 показан этот граф компонент для рассматриваемого выше графа G.

Рис.
9.4.
Граф отношения достижимости на компонентах G

В данном случае имеется одна минимальная компонента K₂.

Во многих приложениях ориентированный граф представляет собой сеть распространения
некоторого ресурса: продукта, товара, информации и т.п. В таких случаях естественно возникает
задача поиска минимального числа таких точек (вершин),
из которых этот ресурс может быть доставлен в любую
точку сети.

Определение 9.12. Пусть G=(V,E) — ориентированный граф.
Подмножество вершин 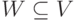называется порождающим,
если из вершин W
можно достичь любую вершину графа.
Подмножество вершин 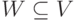называется базой графа,
если оно является порождающим,
но никакое его собственное подмножество порождающим не является.

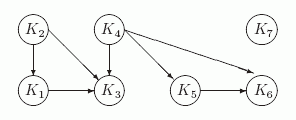
Следующая теорема позволяет эффективно находить все базы графа.

Теорема 9.1.
Пусть G=(V,E) — ориентированный граф. Подмножество вершин
является базой G тогда и только тогда, когда содержит по одной вершине из каждой
минимальной компоненты сильной связности G и не содержит никаких других вершин.

Доказательство Заметим вначале, что каждая вершина графа достижима из вершины,
принадлежащей некоторой минимальной компоненте. Поэтому множество вершин W,
содержащих по одной вершине из каждой минимальной компоненты, является порождающим
а при удалении из него любой вершины перестает быть таковым, так как вершины из
соответствующей минимальной компоненты становятся недостижимы. Поэтому W является базой.

Обратно, если W является базой, то оно обязано включать хотя бы по одной вершине
из каждой минимальной компоненты, иначе вершины такой минимальной компоненты окажутся
недоступны. Никаких других вершин W содержать не может, так как каждая из них
достижима из уже включенных вершин.

Из этой теоремы вытекает следующая процедура построения одной или перечисления всех баз графа G.

Найти все компоненты сильной связности G.
Определить порядок на них и выделить минимальные относительно этого порядка компоненты.
Породить одну или все базы графа, выбирая по одной вершине из каждой минимальной компоненты.

Пример 9.5.
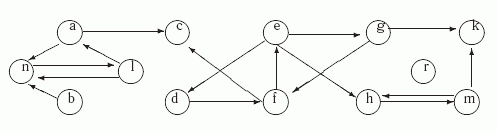
Определим все базы ориентированного графа G, показанного на рис.9.5.

Рис.
9.5.
Граф G

На первом этапе находим компоненты сильной связности G:

$K_1 ={ a, n, l }, K_2 = { b }, K_3 ={ c}, K_4 ={ d,e, f, g}, \ K_5={ h, m}, K_6 ={ k}, K_7= { r}$

На втором этапе строим граф строгой достижимости на этих компонентах.

Рис.
9.6.
Граф отношения достижимости на компонентах G

Определяем минимальные компоненты: K₂ = { b }, K₄ ={ d,e, f, g} и K₇= { r}.

Наконец перечисляем все четыре базы G: B₁= { b, d, r}, B₂= { b, e, r}, B₃= { b, f, r} и B₁= { b, g, r}.

Задачи

Задача 9.1. Докажите, что сумма степеней всех вершин произвольного ориентированного графа четна.

У этой задачи имеется популярная интерпретация: доказать, что общее число
рукопожатий, которыми обменялись люди, пришедшие на вечеринку,
всегда четно.

Задача 9.2. Перечислите все неизоморфные неориентированные графы, у которых не
более четырех вершин.

Задача 9.3.
Докажите, что неориентированный связный граф остается связным после
удаления некоторого ребра 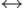это ребро принадлежит некоторому циклу.

Задача 9.4.
Докажите, что неориентированный связный граф с n вершинам и

содержит не менее n-1 ребер,
если содержит больше n-1 ребер, то имеет, по крайней мере, хотя бы один цикл.

Задача 9.5.
Докажите, что в любой группе из 6 человек есть трое попарно знакомых или
трое попарно незнакомых.

Задача 9.6.
Докажите, что неориентированный граф G=(V,E) связен
для каждого разбиения $V= V_{1}cup V_{2}$ с непустыми V₁ и V₂ существует ребро, соединяющее V₁ с V₂.

Задача 9.7.
Докажите, что, если в неориентированном графе имеется ровно две вершины нечетной
степени, то они связаны путем.

Задача 9.8.
Пусть G=(V,E) неориентированный граф с |E| < |V|-1. Докажите, что тогда G несвязный граф.

Задача 9.9. Докажите, что в связном неориентированном графе
любые два простых пути максимальной длины имеют общую вершину.

Задача 9.10.
Пусть неориентированный граф без петель G=(V,E) имеет k компонент связности. Доказать, что тогда

Задача 9.11. Определите, что представляет из себя граф достижимости для

графа с n вершинам и и пустым множеством ребер;
графа с n вершинам и: V= {v₁,… , v_n}, ребра которого образуют цикл:

$E ={(v_1,v_2), (v_2,v_3), ldots , (v_{n-1},v_n), (v_n,v_1) }.$

Задача 9.12. Вычислите матрицу графа достижимости 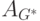$A_{G^*}$ для графа

$G=({a,b,c,d,e,f, g}, { (a,b), (b,a), (a,c), (b,d), (e,d), \(d, f), (f,c), (c,f), (g,e)}$

и постройте соответствующий ей граф достижимости. Найдите все базы графа G.

Задача 9.13.
Построить для заданного на рис. 9.7 ориентированного графа G₁=(V,E)
его матрицу смежности A_G1, матрицу инцидентности B_G1
и списки смежности. Вычислить матрицу достижимости A_G1*
и построить соответствующий граф достижимости G₁^*.