Как найти количество точек информатика

Привет! Сегодня разберём новый тип 6 задания из ЕГЭ по информатике 2023! Добавим недостающий пазл в видеокурс по подготовке к ЕГЭ по информатике.

Так же Вы можете посмотреть разбор 6 задания из ДЕМОВЕРСИИ 2023.

На мой взгляд, на экзамене скорее всего будет задача, похожая именно на демонстрационный вариант. Т.к. это задание нового образца, то выпускникам необходимо привыкнуть к нему.

Вспомним, когда в прошлом году была введена новая формулировка для 3 задания, то на экзамене дали очень похожую задачу на ту, которая была в демоверсии.

Рассмотрим первую тренировочную задачу из 6 задания ЕГЭ по информатике 2023.

Задача (Элегантный способ)

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись

Повтори k [Команда1 Команда2 … КомандаS]

означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:

Повтори 15 [Вперёд 15 Направо 120]

Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

Решение:

В начале нужно понять, какая фигура получится в результате действий Исполнителя Черепахи.

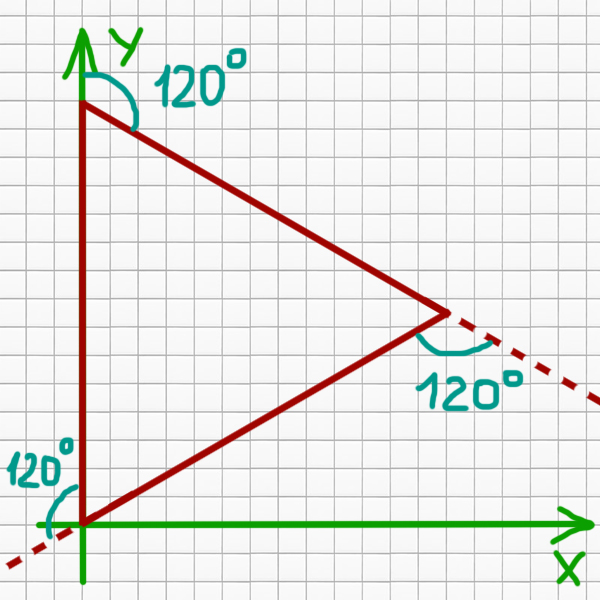
Черепаха идёт вверх на 15 единиц. Потом поворачивает направо на 120 градусов. Потом идёт на 15 единиц по заданному курсу и снова поворачивает на 120 градусов, идёт на 15 единиц ещё и попадает в исходную точку. В итоге получается равносторонний треугольник! Дальнейшие повторения не имеют смысла, т.к. нового больше ничего не нарисуется.

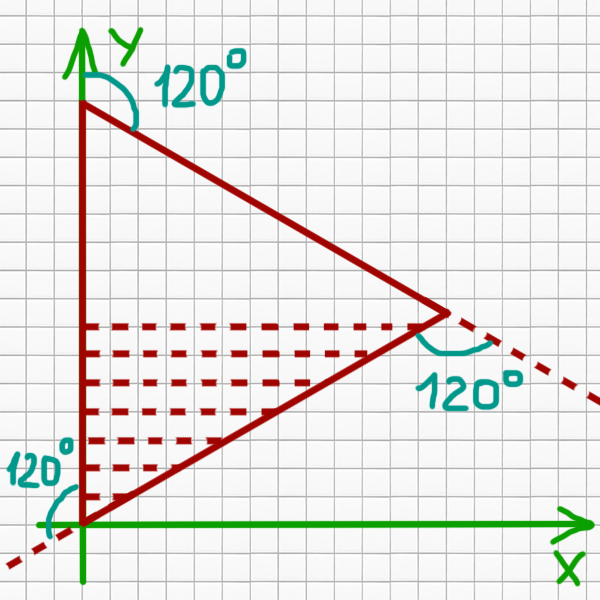
Проведём перпендикуляры от каждой точки с целыми координатами на оси Y внутри треугольника.

Для каждой точки на оси Y мы можем найти этот перпендикуляр. Это и есть искомое количество точек на каждой такой линии, если округлить это значение в меньшую сторону.

Посмотрим, как найти такой перпендикуляр, если точка на оси Y находится до середины стороны. Пусть есть точка (0, y_n), а d_n — это перпендикуляр для этой точки. Тогда

tg(60^o) = d_n / y_n
d_n = tg(60^o) * y_n

Для второй половины длины перпендикуляров будут такие же.

Напишем программу на Питоне, которая подсчитает все точки.

import math

s=0

for y in range(0, 8):
    s = s + int(math.tan(math.pi / 3) * y )

s = 2*s

print(s)

Нам необходимо взять первые 7 точек, дальше ситуация симметричная. Пишем в цикле for 8, потому что последнее число не проходится в Питоне.

Вычисляем по формуле длину каждого перпендикуляра. Тангенс вычисляется с помощью функции math.tan. Для неё нужна математическая библиотека math. Функция должна получить градусы в радианах, поэтому ей передаём π/3 = 60^o.

В цикле суммируем все точки для каждой линии. Результат нужно умножить на 2, чтобы учесть вторую половину треугольника.

Ответ: 90

Задача(Считаем точки вручную)

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Налево m (где m – целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись

Повтори k [Команда1 Команда2 … КомандаS]

означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:

Повтори 16 [Налево 36 Вперёд 4 Налево 36]

Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии следует учитывать.

Решение:

В это задачке достаточно не просто составить уравнения прямых полученной фигуры. В таких случаях можно попробовать вручную посчитать точки с помощью известной программы Кумир от НИИСИ РАН. Скачать её можно с официального сайта НИИСИ РАН.

Вероятно, это программа окажется на компьютере на экзамене.

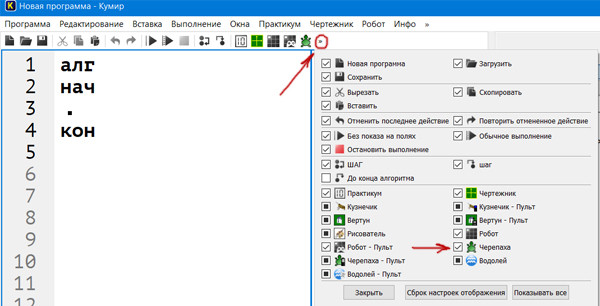
Запустим программу Кумир-Стандарт. В начале нужно подключить модуль Черепаха.

После того, как модуль Черепаха подключён, можно написать программу на языке Кумир.

использовать Черепаха
алг
нач
  опустить хвост
  нц 16 раз
    влево(36)
    вперед(4)
    влево(36)
  кц
кон

В начале нужно подключить модуль Черепаха. Слово алг обозначает начало алгоритма. Слово нач — это начало программы.

Опускаем хвост у Черепахи. Цикл пишем с помощью команды нц — начало цикла. Команда кц — это конец цикла. Команда влево — это аналог команды Налево (видим, что эти команды пишутся по-разному). Аналогично есть команда вправо в программе Кумир. Команда вперед пишется без буквы ё.

После того, как алгоритм перенесли в программу Кумир, запускаем программу, нажав на кнопку F9 (или кнопка плей в виде треугольника).

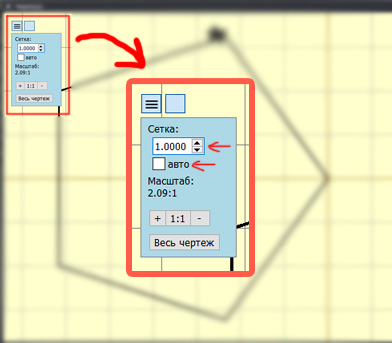
После этого появится окно в правом нижнем углу. Это окно можно расширить до приемлемых размеров, чтобы нам было удобно анализировать рисунок.

Необходимо настроить масштабирование на 1.

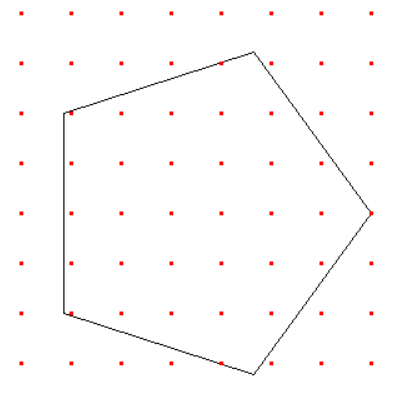
После этого можно сделать скриншот и перенести рисунок в программу Paint, где и посчитать точки вручную.

Получается в ответе 31 точка. Обратите внимание, что в этой задачи просили подсчитать точки, которые находятся на линиях в том числе.

Даже если нет программы Кумир, можно подсчитать точки вручную через Python. Напишем программу.

from turtle import *

left(90)
for i in range(16):
    left(36)
    forward(4*40)
    left(36)

penup()
for x in range(-10, 10):
    for y in range(-10, 10):
        setpos(x*40, y*40)
        dot(4, 'red')

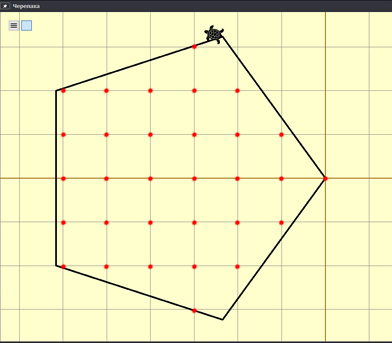
Программа выведет такую картину.

В программе подключаем модуль turtle. В начале повернём Черепаху на 90 градусов налево, с помощью команды left. Это делается из-за того, в Python Черепаха смотрит вдоль положительного направления оси абсцисс.

Далее идёт цикл, который указан в задаче. Он должен повторится 16 раз. Внутри цикла пишем программу для Черепахи. Команда left() — поворот налево (аналогично right() — поворот направо), команда forward() — это движение верёд.

4 единицы внутри команды forward() умножаются на 40. Число 40 — это коэффициент размера нашего рисунка. Попробуйте «поиграть» с этим числом, чтобы посмотреть эффект уменьшения или увеличения рисунка.

Команда penup() позволяет поднять кисть, чтобы проставить точки, которые будут символизировать точки с целыми координатами.

Далее идут вложенные циклы, с помощью них мы проставим точки с целыми координатами. Выбираем диапазон, чтобы наша фигура точно уместилась.

Команда setpos() ставим точки. Умножаем координаты x и y на тот же коэффициент, что использовали ранее.

Команда dot() устанавливает жирность и цвет точки.

Ответ: 31

Задача (Составляем уравнения)

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост поднят. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует три команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке; Опусти, принуждающая Черепаху опустить хвост.

Запись Повтори k [Команда 1 Команда 2 … Команда S] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:

Вперёд 100 Направо 90 Вперёд 100 Направо 30 Опусти Повтори 10 [Вперёд 25 Направо 90]

Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

Решение:

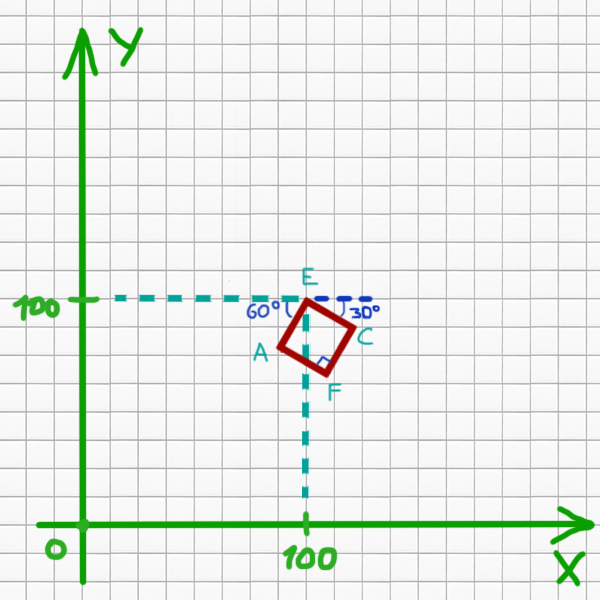
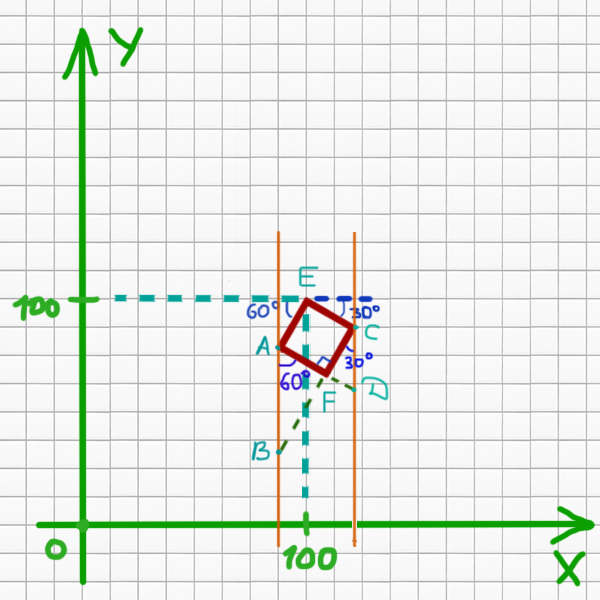
Нарисуем общий рисунок.

Здесь уже не очень удобно пользоваться элегантным способом. Составим уравнения прямых, которые образуют квадрат. Общий вид уравнения прямой выглядит так:

y=k*x+b

Коэффициент k — это тангенс угла наклона α к оси X ( 0 ≤ α < π, но α ≠ π/2). Число b — это смещение прямой по оси Y относительно нуля.

Для прямой AE k₁=tan(60^o)=√3. Так же она проходит через точку (100, 100).

Найдём число b. Подставим в общее уравнение координаты точки (100, 100):

y = k*x+b = √3*100 + b = 100
b=100*(1 — √3)

Получается уравнение прямой AE:

y= √3*x + 100(1 — √3)

Найдём на сколько смещена FC по оси Y относительно AE.

cos(60^o) = 25 (сторона квадрата) / AB

AB = 25 / cos(60^o) = 25 / 0,5 = 50

Получается, что уравнение для прямой FC:

y=√3*x + 100(1 — √3) — 50

Для прямой EC k₂=-tan(30^o) = — √3/3. Эта прямая тоже проходит через точку (100, 100). Подставим эти координаты в уравнение и найдём b.

y = (-√3/3) * x + b = (-√3/3) * 100 + b = 100
b = 100(1 + √3/3)

Тогда уравнение для прямой EC получается:

y = (-√3/3) * x + 100(1 + √3/3)

Найдём на сколько смещена прямая AF относительно EC по оси Y.

cos(30^o) = 25 (длина стороны) / CD
CD = 25 / cos(30^o) = 25 / (√3/2) = 50/√3

Тогда для прямой AF:

y = (- √3/3) * x + 100(1 + √3/3) — 50/√3

Пробежимся с помощью Питона для переменной x от 0 до 150. Для переменной y от 0 до 100. Чтобы получить точку, используем вложенные циклы!

s=0

for x in range(1, 200):
    for y in range(1, 200):
        if (y < (3**0.5)*x + 100*(1-3**0.5)) and (y > (3**0.5)*x + 100*(1-3**0.5) - 50) and (y < (- 3**0.5 / 3)*x + 100*(1+ 3**0.5 / 3)) and (y > (-3**0.5/3)*x + 100*(1 + 3**0.5 /3) - 50 / 3**0.5 ):
            s=s+1

print(s) 

Точки, которые лежат в квадрате должны удовлетворять следующим условиям:

Точки должны быть ниже прямых AE и EC, но выше AF и FC

Проверить выше или ниже некоторая точка M(x_m, y_m), чем прямая y=k*x+b, можно следующим образом:

Если y_m > k*x_m + b, то точка лежит выше прямой.
Если y_m < k*x_m + b, то точка лежит ниже прямой.

Данный принцип и был использован в программе.

Ответ: 625

Задача (Закрепление)

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует три команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке; Опусти, принуждающая Черепаху опустить хвост.

Запись Повтори k [Команда 1 Команда 2 … Команда S] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:

Повтори 21 [Вперёд 31 Направо 60]

Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

Копирование прямо
Решение:

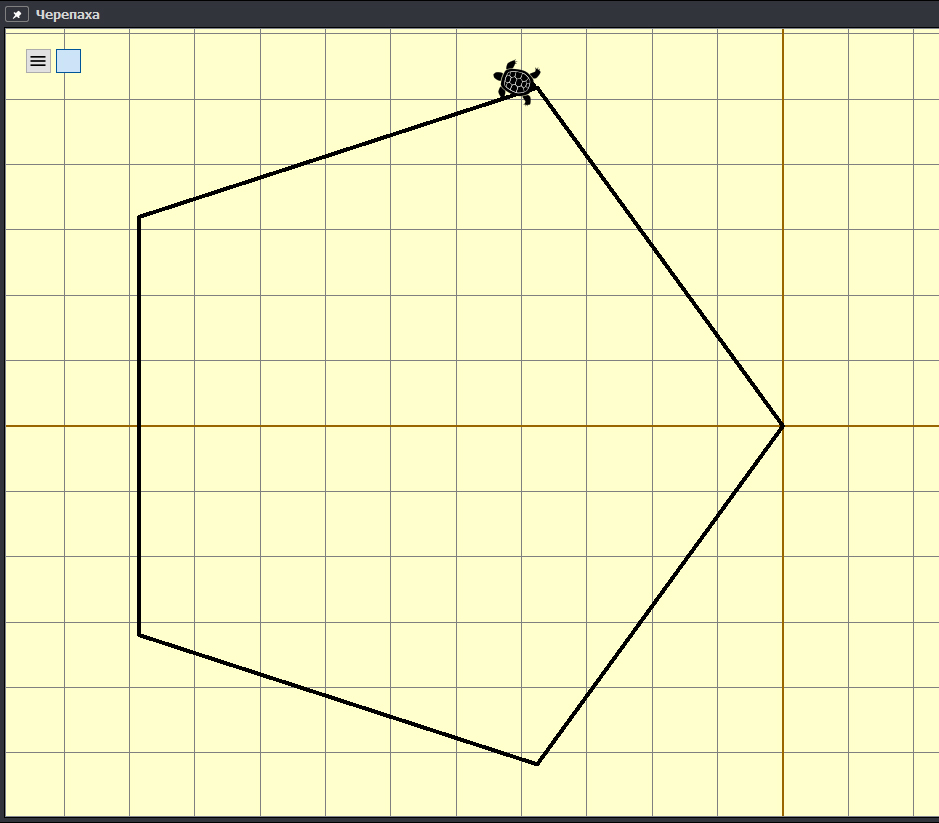
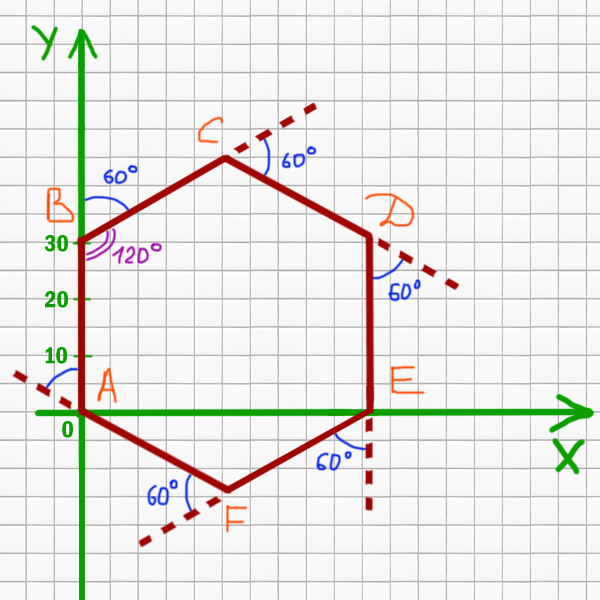
Попробуем понять, какая фигура получится в итоге.

Получается правильный шестиугольник. Угол ∠СВА = 120^o. Как раз угол правильного n-угольника равен (n-2)*180^o/n. Для шестиугольника получается (6-2)*180^o/6 = 120^o.

Будем решать методом составления уравнений.

Рассмотрим прямую BC. Если провести от точки B прямую параллельную оси X, то мы увидим, что угол наклона прямой BC равен 30^o.

y = tan(30^o)*x + 31
y = (√3/3) * x + 31

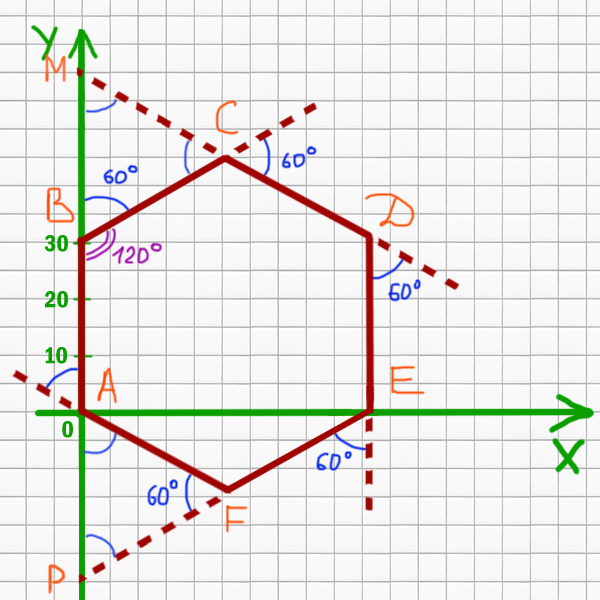
Прямая DC имеет угол наклона -30^o к оси X. Она расположена выше, чем BC на МВ. Треугольник BCM равносторонний. Значит, МВ=31. Тогда уравнение для DC будет:

y = -(√3/3) * x + 62

Уравнение для AF будет:

y = -(√3/3) * x

Прямая EF имеет угол наклона 30^o относительно оси X. Смещена она вниз на AP. Треугольник AFP так же является равносторонним. Следовательно, AP = 31. Тогда для EF получается:

y=tan(30^o)*x — 31
y=(√3/3)*x — 31

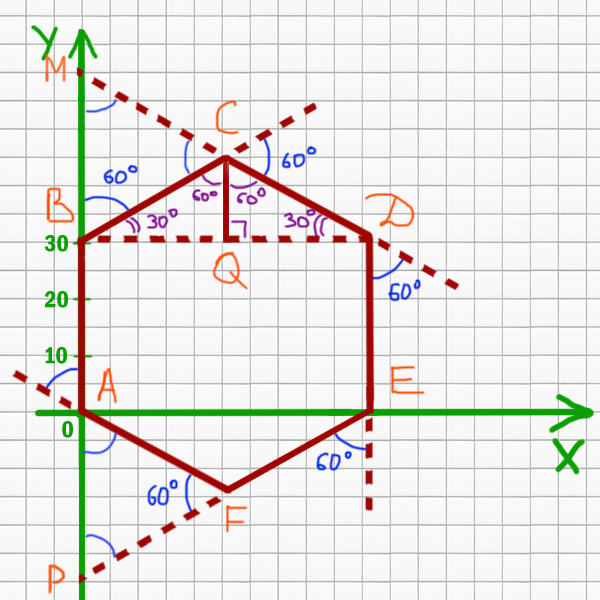
Прямая AB это x=0. Найдём так же ED.

cos(30^o) = BQ / BC
BQ = BC * cos(30^o)
BQ = 31 * (√3/2)
BD = 2 * BQ = 2 * 31 * (√3/2) = 31 * √3

Значит, уравнение для ED: x = 31 * √3.

Когда уравнения готовы, можно написать программу.

k=0
for x in range(-100, 100):
    for y in range(-100, 100):
        if (y < 3**0.5 / 3 * x + 31) and (y < -(3**0.5) / 3 * x + 62) and (y > -(3**0.5) / 3 * x) and (y > 3**0.5 / 3 * x - 31) and (x > 0) and (x < 31 * 3**0.5):
            k=k+1
print(k)

Точки должны быть ниже прямых BC и CD, но выше прямых AF и EF. Так же координаты x должны быть 0 < x < 31 * √3.

Важно не забыть для y пробежаться и по отрицательным значениям, т.к. фигура находится меньше оси X.

Ответ: 2476

На сегодня всё. Удачи при решение 6 задания из ЕГЭ по информатике 2023.

Задачи, связанные с определением количества информации, занимают довольно большое место как в общем курсе 9-11 классов, так и при итоговой аттестации разного типа.

Обычно решение подобных задач не представляет трудности для учащихся с хорошими способностями к анализу ситуаций. Но большинство учеников поначалу путаются в понятиях и не знают, как приступить к решению.

Тем не менее, к 9-му классу учащиеся уже имеют определенный опыт решения задач по другим предметам (более всего – физика) с применением формул. Определить, что в задаче дано, что необходимо найти, и выразить одну переменную через другую – действия довольно привычные, и с ними справляются даже слабые ученики. Представляется возможным ввести некоторые дополнительные формулы в курсе информатики и найти общий стиль их применения в решении задач.

Оттолкнемся от одной из главных формул информатики – формулы Хартли N=2ⁱ. При ее использовании учащиеся могут еще не знать понятия логарифма, достаточно вначале иметь перед глазами, а затем запомнить таблицу степеней числа 2 хотя бы по 10-й степени.

При этом формула может применяться в решении задач разного типа, если правильно определить систему обозначений.

Выделим в системе задач на количество информации задачи следующих типов:

1. Количество информации при вероятностном подходе;
2. Кодирование положений;
3. Количество информации при алфавитном подходе (кодирование текста);
4. Кодирование графической информации;
5. Кодирование звуковой информации

Все задачи группы A (в случае, если мы имеем дело с равновероятными событиями) решаются непосредственно по формуле Хартли с ее привычными обозначениями:

• N – количество равновероятных событий;
• i – количество бит в сообщении о том, что событие произошло,

Причем в задаче может быть определена любая из переменных с заданием найти вторую. В случае если число N не является непосредственно числом, представляющим ту или иную степень числа 2, количество бит нам необходимо определить «с запасом». Так для гарантированного угадывания числа в диапазоне от 1 до 100 необходимо задать минимально 7 вопросов (27=128).

Решение задач для случаев неравновероятных событий в этой статье не рассматривается.

Для решения задач групп B-E дополнительно введем еще одну формулу:

Q=k*i

и определим систему обозначений для задач разного типа.

Для задач группы B значение переменных в формуле Хартли таково:

• i – количество «двоичных элементов», используемых для кодирования;
• N – количество положений, которые можно закодировать посредством этих элементов.

Так:

• два флажка позволяют передать 4 различных сообщения;
• с помощью трех лампочек можно потенциально закодировать 8 различных сигналов;
• последовательность из 8 импульсов и пауз при передаче информации посредством электрического тока позволяет закодировать 256 различных текстовых знаков;

и т.п.

Рассмотрим структуру решения по формуле:

Задача 1: Сколько существует различных последовательностей из символов «плюс» и «минус» длиной ровно в пять символов?

Дано: i = 5

Найти: N

Решение: N = 2⁵

Ответ: 5

Каждый элемент в последовательности для кодирования несет один бит информации.

Очевидно, что при определении количества элементов, необходимых для кодирования N положений, нас всегда интересует минимально необходимое для этого количество бит.

При однократном кодировании необходимого количества положений мы определяем необходимое количество бит и ограничиваемся формулой Хартли. Если кодирование проводится несколько раз, то это количество мы обозначаем как k и, определяя общее количество информации для всего кода (Q), применяем вторую формулу.

Задача 2: Метеорологическая станция ведет наблюдение за влажностью воздуха, результатом которых является целое число от 1 до 100%, которое кодируется посредством минимально возможного количества бит. Станция сделала 80 измерений. Какой информационный объем результатов наблюдений.

Дано: N = 100; k = 80

Найти: Q

Решение:

По формуле Хартли i = 7 (с запасом); Q = 80 * 7 = 560

Ответ: 560 бит

(Если в задаче даны варианты ответов с использованием других единиц измерения количества информации, осуществляем перевод: 560 бит = 70 байт).

Отметим дополнительно, что, если для кодирования используются нe «двоичные», а скажем, «троичные» элементы, то мы меняем в формуле основание степени.

Задача 3: Световое табло состоит из лампочек. Каждая из лампочек может находиться в одном из трех состояний («включено», «выключена» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов.

В данном случае N = 18, основание степени – 3. Необходимо найти i. Если логарифмы еще не знакомы, определяем методом подбора – 5. Ответ: 5 лампочек

Далее рассмотрим решение задач на кодирование текстовой, графической и звуковой информации.

Здесь важно провести параллели:

Информация, которая обрабатывается на компьютере, должна быть представлена в виде конечного множества элементов (символ для текста, точка – для графики, фрагмент звуковой волны – для звука), каждый из которых кодируется отдельно с использованием заданного количества бит. Зависимость количества элементов, которые могут быть закодированы, от количества бит, отводимых, на кодирование одного элемента, как и раньше, определяем по формуле Хартли.

А путем умножения количества элементов (k) на «информационный вес» одного из них, определяем общее количество информации в текстовом, графическом, звуковом фрагменте (Q).

Каждую задачу можно решить, обозначив заданными переменными известные данные, и выразив одну переменную через другую. Только необходимо помнить, что непосредственно расчеты чаще всего производятся в минимальных единицах измерения (битах, секундах, герцах), а потом, если необходимо, ответ переводится в более крупные единицы измерения.

Рассмотрим конкретные примеры:

Алфавитный подход позволяет определить количество информации, заключенной в тексте. Причем под «текстом» в данном случае понимают любую конечную последовательность знаков, несущую информационную нагрузку. Поэтому обозначения переменных для задач группы C одинаково применимы как для задач на передачу обычной текстовой информации посредством компьютера (i = 8, N = 256 или i = 16, N = 16256) так и для задач на передачу сообщений посредством любых других алфавитов (здесь и далее используются разные названия, встречающиеся в задачах):

• i – количество бит, используемое для кодирования одного текстового знака, равнозначно: количество информации (в битах), в нем содержащееся, информационный «вес», информационный «объем» одного знака;
• N – полное количество знаков в алфавите, используемом для передачи сообщения, мощность алфавита;
• k – количество знаков в сообщении;
• Q – количество информации в сообщении (информационный «вес», «объем» сообщения), количество памяти, отведенное для хранения закодированной информации;

Задача 4: Объем сообщения – 7,5 кбайт. Известно, что данное сообщение содержит 7680 символов. Какова мощность алфавита?

Дано:

Q = 7,5 Кбайт = 7680 байт ( в данном случае нет необходимости перевода в биты);

k = 7680

Найти: N

Решение: i = Q / k = 1 байт = 8 бит; N = 2⁸ = 256

Ответ: 256 знаков

Задача 5: Дан текст из 600 символов. Известно, что символы берутся из таблицы размером 16 на 32. Определите информационный объем текста в битах.

Дано:

k = 600; N = 16 * 32

Найти: Q

Решение:

N = 2⁴ * 2⁵ = 2⁹; i = 9; Q = 600 * 9 = 5400 бит;

Ответ: 5400 бит

Задача 6: Мощность алфавита равна 64. Сколько кбайт памяти потребуется, чтобы сохранить 128 страниц текста, содержащего в среднем 256 символов на каждой странице?

Дано:

N = 64; k = 128 * 256

Найти: Q

Решение:

64 = 2ⁱ; i = 6; Q = 128 * 256 * 6 = 196608 бит = 24576 байт = 24 Кбайт;

Ответ: 24 Кбайт

Задача 7: Для кодирования нотной записи используется 7 значков-нот. Каждая нота кодируется одним и тем же минимально возможным количеством бит. Чему равен информационный объем сообщения, состоящего из 180 нот?

Дано:

N = 7; k = 180

Найти: Q

Решение:

7 = 2ⁱ; i = 3 (с запасом); Q = 180 * 3 = 540 бит;

Ответ: 540 бит

Рассматривая задачи групп D и E, вспоминаем, что при кодировании графики и звука производится дискретизация, то есть разбиение изображения на конечное множество элементов (пикселей) и звуковой волны на конечное множество отрезков, количество которых зависит от количества измерений в секунду уровня звука (частоты дискретизации) и времени звучания звукового файла.

То есть –

• общее количество элементов в графическом файле (k) равно разрешению изображения или разрешению экрана монитора, если изображение формируется на весь экран,
• общее количество элементов в звуковом файле (k) равно произведению частоты дискретизации на время звучания (важно при этом использовать в качестве единиц измерения минимальные единицы – герцы и секунды).

Рассмотрим всю систему обозначений для данного типа задач:

• i – количество бит, используемое для кодирования одного элемента изображения или звукового фрагмента, равнозначно: глубина цвета, звука;
• N – насыщенность цвета, равнозначно: количество цветов в палитре изображения, цветовое разрешение изображения; насыщенность звука (в задачах обычно не используется);
• k – количество точек в изображении, равнозначно: разрешение изображения (или экрана) или количество фрагментов дискретной звуковой волны (равно произведению частоты дискретизации на время звучания);
• Q – количество информации, содержащееся в графическом (звуковом) файле, равнозначно: информационный «объем», «вес» графического (звукового) файла, объем памяти (видеопамяти), необходимый для хранения заданного файла.

Задача 8: Для хранения растрового изображения размером 64 на 64 пикселя отвели 512 байтов памяти. Каково максимально возможное число цветов в палитре изображения?

Дано:

k = 64 * 64 = 212; Q = 512 байтов = 29 * 23 = 212 бит;

Найти: N

Решение:

i = Q / k = 2¹² / 2¹² = 1; N = 21 = 2

Ответ: 2 цвета

Задача 9: Сколько памяти нужно для хранения 64-цветного растрового графического изображения размером 32 на 128 точек?

Дано:

N = 64; k = 32 * 128;

Найти: Q

Решение:

i = 6 (по формуле Хартли); Q = 32 * 128 * 6 = 24576 бит = 3072 байт = 3 Кбайт

Ответ: 3 Кбайт

Задача 10: Оцените информационный объем моноаудиофайла длительностью звучания 1 минута, если глубина кодирования равна 16 бит при частоте дискретизации 8 кГц

Дано:

k = 60 * 8000; i = 16;

Найти: Q

Решение:

Q = 60 * 8000 * 16 = 7680000 бит = 960000 байт = 937,5 Кбайт

Ответ: 937,5 Кбайт

(Если файл стерео, Q будет больше в 2 раза).

Задача 11: Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен 625 Кбайт

Дано:

i = 16; k = 32000 * t; Q = 625 кбайт = 640000 байт = 5120000 бит;

Найти: t

Решение:

k = Q / i; k = 5120000 / 16 = 320000; t = 320000 / 32000 = 10 сек

Ответ: 10 секунд

В эту же схему укладывается решение задач на скорость передачи информации любого типа, если в хорошо известной учащимся формуле:

S = V * t принять S = Q (количество переданной информации вместо расстояния).

Задача 12: Сколько секунд потребуется обычному модему, передающему сообщения со скоростью 28800 бит/сек, чтобы передать цветное растровое изображение размером 640 на 480 пикселей, при условии, что цвет каждого пикселя кодируется тремя байтами?

Дано:

V = 28800 бит/сек; k = 640 * 480; i = 3 байт = 24 бит;

Найти: t

Решение:

t = S (Q) / V; Q = k * i = 640 * 480 * 24 = 7372800 бит; t = 7372800 / 28800 = 256 сек.

Ответ: 256 сек

В заключение отметим, что после определенной тренировки решения задач по формулам, многие учащиеся перестают нуждаться в их прописывании в задаче, сразу определяя порядок необходимых арифметических действий для ее решения.

Урок
«Вычисление
объема графического файла»

                                                        Кодирование
графической информации

Вычисление объема графического
файла

Информации о состоянии каждого пикселя
хранится в закодированном виде в памяти ПК. Из основной формулы информатики
можно подсчитать объем памяти, необходимый для хранения одного пикселя:

Вычисление
объема растрового изображения

Задача 1. Вычислить объем
растрового черно-белого изображения размером 100 х 100.

Решение: V = K * i = 100 x 100 x 1 бит = 10
000 бит / 8 бит = 1250 байт / 1024 = 1,22 Кбайт.

Ответ: 1,22 Кбайт

Задача 2. Вычислить объем
растрового изображения размером 100 х 100 и палитрой 256 цветов.

Решение: 1)  256 = 2 ⁱ ,  i = 8 

                 
2) V = K * i = 100 x 100 x 8 бит
= 100 x 100 x 1
байт = 10 000 байт / 1024 = 9,76 Кбайт.

Ответ: 9,76 Кбайт

                                                          
Вычисление объема векторного изображения

Задача
3. Вычислить
объем векторного изображения.

Решение: Векторное
изображение формируется из примитивов и хранится в памяти в виде формулы:

RECTANGLE 1, 1, 100,  100,
Red, Green

                 
Подсчитаем количество символов в этой формуле: 36 символов (букв, цифр, знаков
препинания и пробелов)

                 
36 символов х 2 байта = 72 байт    (Unicode 1
символ — 1 байт)

Ответ: 72 байт

Урок
«Определение объема графического файла»

Задача 
2. Какой объем информации занимает черно-белое изображение 
размером 600 х 800?

Решение:  600
х 800 = 480 000  точек   480 000  точек  х 1 бит = 480
000  бит

480
000  бит / 8 бит / 1024 байт ≈ 58, 59 Кбайт

Ответ: 58, 59 Кбайт

Задача  3. Определить  объем
растрового изображения размером 600 х 800 при глубине цвета 24 бита. 

Решение:  600
х 800 = 480 000  точек 480 000  точек  х 24 бит = 11 520
000  бит

11 520
000 бит / 8 бит / 1024 байт = 1406,25 Кбайт / 1024 байт ≈ 1,37 Мбайт

Ответ: ≈ 1,37 Мбайт

Задача  3.  Определить объем видеопамяти компьютера, который
необходим для реализации графического режима монитора с разрешающей
способностью  1024×768 и палитрой 65536 цветов.

Решение: N 
= 2ⁱ  =  65536       i =  16 бит 
     Количество точек изображения равно:
      1024  х 768 = 786432

16 бит  х 786432 = 12582912 бита / 8 бит / 1024 байт
= 1536 Кбайт / 1024 байт = 1,5 М байта

Ответ: 1,5
М байта

Задача 
4. Определить объем растрового изображения размером  200 х 200
и  256 цветами.

Решение: 200 
х 200 х 8 бит = 320 000 бит / 8 бит / 1024 байт = 39,0625 Кбайт ≈ 39 Кбайт

Ответ: 39 Кбайт

Самостоятельное
решение задач:

Задача 1. Сколько цветов будет в
палитре, если каждый базовый цвет кодировать в 6 битах?

Задача 2.  Для хранения
растрового изображения размером 1024 х 512 пикселей отвели 256 Кбайт памяти.
Каково максимально возможное число цветов в палитре изображения?

Задача 3. Сколько
памяти компьютера требуется для двоичного кодирования 256-цветного рисунка
размером 10 х 10 точек?

Задача 4. Разрешение
экрана монитора – 1024 х 768 точек, глубина цвета – 16 бит. Каков необходимый
объем видеопамяти для данного графического режима?

Задача 5. Объем
видеопамяти равен 512 Кбайт, разрешающая способность дисплея – 800 х 600. Какое
максимальное количество цветов можно использовать при таких условиях?

Задача 6. Сравнить размеры
видеопамяти, необходимые для хранения изображений:

                    
— 1-е изображение: черно-белое размером 200 х 400

                    
— 2-е изображение: 4 цветное размером 100 х 200

1) первое изображение занимает
памяти больше чем второе на 40000 байтов

2) первое изображение занимает
памяти меньше чем второе на 500 байтов

3) первое изображение занимает
в два раза больше памяти, чем второе

4) первое изображение занимает
в два раза меньше памяти, чем второе

5) оба изображения имеют
одинаковый объем памяти

Домашнее
задание – решить задачи:

Задача 1. Каждой
точке экрана монитора (пикселю) поставлены в соответствие четыре бита, что
позволит отобразить n цветов.        

Задача 2.  Объём видеопамяти равен 4 Мб,
битовая глубина – 24, разрешающая способность дисплея – 640 х 480. Какое
максимальное количество страниц можно использовать при этих условиях?