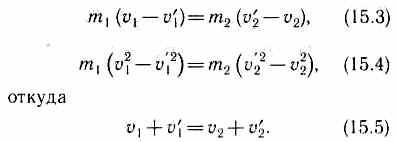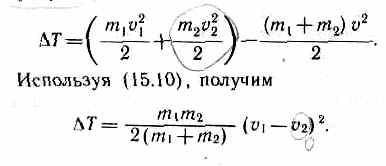Как найти количество теплоты выделившееся при ударе - Avtoru.top

Условие задачи:

Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе двух свинцовых шаров массой 1 кг каждый, скользящих без вращения по абсолютно гладкой поверхности. До удара шары двигались по одной прямой в одном направлении. Скорость первого шара равна 10 см/с, скорость второго – 20 см/с.

Задача №2.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m=1) кг, (upsilon_1=10) см/с, (upsilon_2=20) см/с, (Q-?)

Решение задачи:

Запишем два закона:

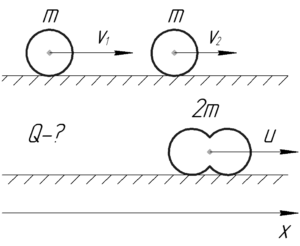
закон сохранения импульса (ЗСИ) в проекции на ось (x), поскольку система, состоящая из двух шаров замкнута в этом направлении;
закон сохранения энергии (ЗСЭ), но учтем, что часть начальной кинетической энергии шаров при абсолютно неупругом ударе переходит в теплоту (Q).

[left{ begin{gathered}
m{upsilon _1} + m{upsilon _2} = 2mu hfill \
frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m{u^2}}}{2} + Q hfill \
end{gathered} right.]

Из ЗСИ выразим скорость шаров после удара:

[u = frac{{{upsilon _1} + {upsilon _2}}}{2}]

Полученное выражение подставим в ЗСЭ:

[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}{left( {frac{{{upsilon _1} + {upsilon _2}}}{2}} right)^2} + Q]

Раскроем квадрат суммы в правой части уравнения:

[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}left( {frac{{upsilon _1^2 + 2{upsilon _1}{upsilon _2} + upsilon _2^2}}{4}} right) + Q]

Откроем скобки:

[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{mupsilon _1^2}}{4} + frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} + Q]

[Q = frac{{mupsilon _1^2}}{4} – frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} = frac{m}{4}left( {upsilon _1^2 – 2{upsilon _1}{upsilon _2} + upsilon _2^2} right)]

[Q = frac{m}{4}{left( {{upsilon _1} – {upsilon _2}} right)^2}]

Получилась “красивая” формула для расчета ответа. Переведем скорости в единицы системы СИ.

[10; см/с = frac{{10}}{{100}}; м/с = 0,1; м/с]

[20; см/с = frac{{20}}{{100}}; м/с = 0,2; м/с]

Считаем ответ:

[Q = frac{1}{4}{left( {0,1 – 0,2} right)^2} = 2,5 cdot 10^{-3}; Дж = 2,5; мДж]

Ответ: 2,5 мДж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с

Источник

Начиная с определений импульса и объяснения законов сохранения, в статье показывается способ решения ряда задач, в которых важно только начальное и конечное состояние (но, например, ничего нельзя сказать про время движения), в частности, задач на столкновение тел.

Введение

С помощью законов сохранения многие механические задачи решаются намного проще, чем при использовании динамических уравнений движений. С другой стороны, законами сохранения можно пользоваться только в тех случаях, когда необходимо, зная начальное состояние тела, найти конечное. При данном описании системы невозможно узнать время движения тела и все промежуточные состояния.

Для лучшего понимания темы различных соударений давайте еще раз повторим теорию по законам сохранения в механике.

Самыми распространенными законами сохранения является закон сохранения импульса и энергии.

Импульс

Определение. Импульсом p тела (материальной точки) называется векторная физическая величина, равная произведению массы m на скорость (здесь и далее жирным шрифтом выделены векторные величины).

p = mv.

Изменение импульса можно представить через второй закон Ньютона:

Δp = mΔv = FΔt

Если рассмотреть систему материальных точек, которые движутся с разными скоростями, то импульс задается следующим выражением:

p = m₁v₁+ m₂v₂ + …

Закон сохранения импульса

При отсутствии внешних сил импульс системы материальных точек сохраняется.

Замечание 1. Отсутствие внешних сил означает, что система замкнута.

Замечание 2. Часто в задачах есть внешние силы, но при этом законом сохранения импульса в каком-то виде пользоваться можно.

Внешние силы есть, но они взаимно скомпенсированы (например сила тяжести и сила нормальной реакции опоры при движении по гладкой поверхности).
Внешние силы не имеют проекции на какую-то заданную ось (например, ось ОX), тогда импульс может сохраняться вдоль этого направления.
Если в некоторый момент времени внутренние силы много больше внешних, тогда импульс системы сохраняется (например, разрыв снаряда)

Так как задачи только на закон сохранения достаточно однообразные, то рассмотрим и закон сохранения энергии.

Работа и энергия

Любая механическая система характеризуется скалярной величиной E — энергией, которая однозначно определяет состояние системы. Зная энергию системы в двух состояниях, можно найти работу внешних сил, совершенную над системой:

ΔE = E₂ – E₁ = A.

Механическая работа

Определение. Если на тело, движущееся по прямой, действует постоянная сила F, то механической работой A этой силы на перемещение s называется скалярное произведение

A = (F, s) = |F||s| · cos(α) = Fs · cos(α),

где α — угол между векторами F и s.

Определение. Средняя мощность <P> силы F — это отношение работы А, совершенной силой F за время t, к интервалу времени t.

<P> = A / t.

Мощность также можно переписать так: <P> = Fv · cos(α).

Консервативные и диссипативные силы

Определение.Консервативные силы (потенциальные силы) —это силы, работа которых при перемещении из состояния 1 в состояние 2 не зависит от траектории, а зависит только от начального и конечного положения точек 1 и 2.

Примеры.Работа силы тяжести или электростатических сил не зависит от траектории, следовательно, это консервативные силы.

К диссипативным силам относятся различные виды силы трения.

Замечание. Работа диссипативных сил всегда отрицательна. Следовательно, они уменьшают механическую энергию тела, переводя ее в тепло.

Кинетическая и потенциальная энергия

Определение. Кинетическая энергия тела равна произведению массы тела на квадрат скорости, деленное на два:

Eкин = mv² / 2.

Так как работа консервативных сил зависит только от начального и конечного положения, то для нее можно определить потенциальную энергию.

Потенциальная энергия для силы тяжести определяется следующим выражением:

Eпот = mgh.

Замечание. Для силы тяжести можно легко вывести потенциальную энергию, зная работу силы притяжения.

Другие примеры.Зная силу растяжения или сжатия пружины, легко посчитать потенциальную энергию сжатой (растянутой) пружины:

Eпот = k(x₂ – x₁)² / 2.

Закон сохранения и изменения энергии

Формулировка. Механическая энергия в замкнутой системе сохраняется при отсутствии диссипативных сил:

ΔE = 0

Замечание 1. Механической энергией называется сумма потенциальной и кинетической энергии.

E = Eкин + Епот.

Замечание 2.При наличии консервативных сил может меняться скорость тела (системы тел) и их общая кинетическая энергия, но это будет происходить за счет перехода кинетической энергии в потенциальную.

Формулировка. Изменение механической энергии под действием внешних и внутренних неконсервативных сил равно суммарной работе этих сил А:

ΔE = A.

Теорема об изменении кинетической энергии

Формулировка. Работа всех сил (консервативных и диссипативных) равна изменению кинетической энергии системы.

∑A = ΔEкин.

Замечание. С помощью этой теоремы легко решать многие задачи. Например, рассмотрим задачу о нахождении тормозного пути автомобиля, движущегося со скоростью v = 60 км/ч по дороге с коэффициетом трения μ = 0,5.

Работа силы трения:

A = –μN = –μmgS,

где N — сила нормальной реакции, S — тормозной путь автомобиля.

Изменение кинетической энергии:

ΔE = –mv² / 2.

По теореме о изменении кинетической энергии:

–mv² / 2 = –μmgS.

S = v² / 2gμ = 29 м

Замечание.Скорость необходимо перевести в СИ.

Соударения

Определение. Центральный удар — это соударение 2 тел , при котором скорости каждого из тел направлены вдоль линии, соединяющей центры обоих тел.

Замечание. Если один из шаров покоится, то скорость второго тела должна быть направлена вдоль линии, соединяющей центры тел.

При решении задач на столкновение двух и более тел надо привыкнуть к следующим формулировкам:

Абсолютно упругий удар (упругий удар) — это тип соударения, при котором выполняется закон сохранения энергии и закон сохранения импульса. Часто этот тип соударения применим к железным шарикам.
Неупругий удар — это удар, при котором выполняется закон сохранения импульса и закон изменения механической энергии (так как теряется часть энергии при ударе).
Абсолютно неупругий удар — это удар, при котором два тела продолжают двигаться как единое целое. При этом столкновении выполняется закон сохранения импульса и закон изменения механической энергии.

Замечание. Как мы видим, для решения задач нужно сначала записать соответствующие законы сохранения энергии и импульса или изменения энергии. Далее необходимо решить получившуюся систему уравнений.

Задача 1

Железный шар массы m = 500 г движется по гладкой горизонтальной поверхности со скоростью 10 м/с и сталкивается с неподвижным восковым шаром, имеющим массу М = 200 г, после чего оба шара движутся вместе. Найдите количество теплоты, выделившееся при ударе.

Решение. В этой задаче удар абсолютно неупругий, поэтому выполняется закон сохранения импульса (ЗСИ) и изменения энергии.

Запишем ЗСИ на ось OX:

mv = (m + M)V. (1)

Для того, чтобы найти выделившуюся энергию при соударении, необходимо записать закон изменения энергии (ЗИЭ)

ΔE = mv² / 2 — (m + M)V² / 2. (2)

Далее остается только математическая часть задачи — решить систему уравнений (1) и (2). Из (1) найдем V:

V = mv / (M + m).

Подставив в (2), получим:

Замечание. Такую задачу невозможно решить для неупругого удара, при котором тела не слипаются друг с другом, так как нам будет неизвестны скорости двух разлетевшихся тел.

Список литературы

Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.

Источник

Брусок массой 400 г, движущийся по гладкой горизонтальной поверхности со скоростью ʋ = 10 м/с, ударяется о такой же, но неподвижный брусок и теряет половину своей скорости. Найдите количество теплоты, выделившейся при соударении брусков. Движение брусков считать поступательным.

Спрятать решение

Решение.

Дано:

m=0,4 кг

υ=10 м/c

Q—?

Решение:

Согласно закону сохранения импульса

откуда скорость второго бруска после соударения

Согласно закону сохранения энергии

откуда количество теплоты, выделившееся при ударе, равно

Подставляя числовые данные условия задачи и проверяя размерность найденной величины, получаем

Ответ: 10 Дж.

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Приведено полное правильное решение, включающее следующие элементы: 1) верно записано краткое условие задачи; 2) записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом; 3) выполнены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ. При этом допускается решение «по частям» (с промежуточными вычислениями).	3
Правильно записаны необходимые формулы, проведены вычисления, и получен ответ (верный или неверный), но допущена ошибка в записи краткого условия или переводе единиц в СИ. ИЛИ Представлено правильное решение только в общем виде, без каких-либо числовых расчётов. ИЛИ Записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом, но в математических преобразованиях или вычислениях допущена ошибка.	2
Записаны и использованы не все исходные формулы, необходимые для решения задачи. ИЛИ Записаны все исходные формулы, но в одной из них допущена ошибка.	1
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла.	0
Максимальный балл	3

Источник

Примером применения
законов сохранения импульса и энергии
при решении реальной физической
задачи является удар абсолютно упругих
и неупругих тел.

Удар
(или соударение)
—
это столкновение двух или более тел,
при котором взаимодействие длится очень
короткое время. Исходя из данного
определения, кроме явлений, которые
можно отнести к ударам в прямом смысле
этого слова

(столкновения
атомов или биллиардных шаров), сюда
можно отнести и такие, как удар человека
о землю при прыжке с трамвая и т. д. При
ударе в телах возникают столь
значительные внутренние силы, что
внешними силами, действующими на
них, можно пренебречь. Это позволяет
рассматривать соударяющиеся тела
как замкнутую систему и применять к ней
законы сохранения.

Тела
во время удара претерпевают деформацию.
Сущность удара заключается в том,
что кинетическая энергия относительного
движения соударяющихся тел на короткое
время преобразуется в энергию упругой
деформации. Во время удара имеет
место перераспределение энергии между
соударяющимися телами. Наблюдения
показывают, что относительная скорость
тел после удара не достигает своего
прежнего значения. Это объясняется
тем, что нет идеально упругих тел и
идеально гладких поверхностей.
Отношение нормальных составляющих
относительной скорости тел после и до
удара называется коэффициентом
восстановления :

 =
v’_n/v_n.

Если
для сталкивающихся тел =0,
то такие тела называются абсолютно
неупругими, если
=1—абсолютно
упругими.

На
практике для всех тел 0<<1
(например, для стальных шаров 0,56,
для шаров из слоновой кости 0,89,
для свинца 0).
Однако в некоторых случаях тела можно
с большой точностью рассматривать либо
как абсолютно упругие, либо как
абсолютно неупругие.

Прямая,
проходящая через точку соприкосновения
тел и нормальная к поверхности их
соприкосновения, называется линией
удара. Удар
называется центральным,
если
тела до удара движутся вдоль прямой,
проходящей через их центры масс. Мы
будем рассматривать только центральные
абсолютно упругие и абсолютно
неупругие удары.

Абсолютно
упругий удар — столкновение
двух тел, в результате которого в обоих
взаимодействующих телах не остается
никаких деформаций и вся кинетическая
энергия, которой обладали тела до удара,
после удара снова превращается в
кинетическую энергию

Для абсолютно
упругого удара выполняются закон
сохранения импульса и закон сохранения
кинетической энергии.

Обозначим
скорости шаров массами m₁
и
m₂
до удара через v₁
и
v₂,
после
удара — через v’₁
и
v’₂
(рис.
18). При прямом центральном ударе
векторы скоростей шаров до и после удара
лежат на прямой линии, соединяющей их
центры. Проекции векторов скорости на
эту линию равны модулям скоростей. Их
направления учтем знаками: положительное
значение припишем движению вправо,
отрицательное — движению влево.

При указанных
допущениях законы сохранения имеют вид

Произведя
соответствующие преобразования в
выражениях (15.1) и (15.2), получим

Решая уравнения
(15.3) и (15.5), находим

Разберем несколько
примеров.

Проанализируем
выражения (15.8) и (15.9) для двух шаров
различных масс:

а) m₁
=m₂.
Если
второй шар до удара висел неподвижно
(v₂=0)
(рис.
19), то после удара остановится первый
шар (v’₁=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(v’₂
= v₁);

б)
m₁>m₂.

Первый
шар продолжает двигаться в том же
направлении, как и до удара, но с меньшей
скоростью (v’₁<v₁).
Скорость
второго шара после удара больше, чем
скорость первого после удара (v’₂>v’₁)
(рис.20);

в)
m₁<m₂.
Направление
движения первого шара при ударе изменяется
— шар отскакивает обратно. Второй шар
движется в ту же сторону, в которую
двигался первый шар до удара, но с меньшей
скоростью, т.е. v’₂<v₁
(рис.
21);

г)
m₂>>m₁
(например,
столкновение шара со стеной). Из уравнений
(15.8) и (15.9) следует, что v’₁=-v₁,
v’₂2m₁v₁/m₂0.

2) При
m₁=m2
выражения
(15.6) и (15.7) будут иметь вид

v’₁=v₂,
v’₂=v₁,

т. е. шары равной
массы «обмениваются» скоростями.

Абсолютно
неупругий удар — столкновение
двух тел, в результате которого тела
объединяются, двигаясь дальше как единое
целое.

Продемонстрировать
абсолютно неупругий удар можно с
помощью шаров из пластилина (глины),
движущихся навстречу друг другу (рис.
22).

Если
массы шаров m₁
и
m₂,
их скорости до удара v₁
и
v₂,
то,
используя закон сохранения импульса,
можно записать

Если
шары движутся навстречу друг другу, то
они вместе будут продолжать двигаться
в ту сторону, в которую двигался шар,
обладающий большим импульсом. В частном
случае если массы шаров равны (m₁=m₂),
то

v
= (v₁+v₂)/2.

Выясним, как
изменяется кинетическая энергия
шаров при центральном абсолютно
неупругом ударе. Так как в процессе
соударения шаров между ними дей-

ствуют силы,
зависящие не от самих деформаций, а от
их скоростей, то мы имеем дело с силами,
подобными силам трения, поэтому закон
сохранения механической энергии не
должен соблюдаться. Вследствие деформации
происходит «потеря» кинетической
энергии, перешедшей в тепловую или
другие формы энергии. Эту «потерю» можно
определить по разности кинетической
энергии тел до и после удара:

Если
ударяемое тело было первоначально
неподвижно (v₂=0),
то

Когда
m₂>>m₁
(масса
неподвижного тела очень большая), то
v<<v₁
и
почти
вся кинетическая энергия тела при ударе
переходит в другие формы энергии.
Поэтому, например, для получения
значительной деформации наковальня
должна быть массивнее молотка.
Наоборот, при забивании гвоздей в стену
масса молотка должна быть гораздо
большей (m₁>>m₂),
тогда
vv₁
и
практически вся энергия затрачивается
на возможно большее перемещение гвоздя,
а не на остаточную деформацию стены.

Абсолютно неупругий
удар — пример того, как происходит
«потеря» механической энергии под
действием диссипативных сил.

Контрольные
вопросы

• В чем различие
между понятиями энергии и работы?

• Как найти
работу переменной силы?

• Какую работу
совершает равнодействующая всех сил,
приложенных к телу, равномерно движущемуся
по окружности?

• Что такое
мощность? Вывести ее формулу.

• Дайте определения
и выведите формулы для известных вам
видов механической энергии. • Какова
связь между силой и потенциальной
энергией?

• Почему изменение
потенциальной энергии обусловлено
только работой консервативных сил?

• В чем заключается
закон сохранения механической энергии?
Для каких систем он выполняется?

• Необходимо
ли условие замкнутости системы для
выполнения закона сохранения механической
энергии?

• В чем физическая
сущность закона сохранения и превращения
энергии? Почему он является фундаментальным
законом природы?

• Каким свойством
времени обусловливается справедливость
закона сохранения механической энергии?

• Что такое
потенциальная яма? потенциальный барьер?

• Какие заключения
о характере движения тел можно сделать
из анализа потенциальных кривых?

• Как
охарактеризовать положения устойчивого
и неустойчивого равновесия? В чем их
различие?

• Чем отличается
абсолютно упругий удар от абсолютно
неупругого?

• Как определить
скорости тел после центрального абсолютно
упругого удара? Следствием каких законов
являются эти выражения?

Задачи

3.1. Определить:
1) работу поднятия груза по наклонной
плоскости; 2) среднюю и 3) максимальную
мощности подъемного устройства, если
масса груза 10 кг, длина наклонной
плоскости 2 м, угол ее наклона к горизонту
45°, коэффициент трения 0,1 и время подъема
2 с. [1) 170 Дж; 2) 85 Вт; 3) 173 Вт |

3.2. С башни высотой
35 м горизонтально брошен камень массой
0,3 кг. Пренебрегая сопротивлением
воздуха, определить: 1) скорость, с которой
брошен камень, если через 1 с после начала
движения его кинетическая энергия 60
Дж; 2) потенциальную энергию камня через
1 с после начала движения. [1) 17,4 м/с; 2)
88,6 Дж ]

3.3. Пренебрегая
трением, определить наименьшую высоту,
с которой должна скатываться тележка
с человеком по желобу, переходящему в
петлю радиусом 10 м, чтобы она сделала
полную петлю и не выпала из желоба. [25
м]

3.4.
Пуля массой m=
10 г, летевшая горизонтально со скоростью
v
= 500 м/с, попадает в баллистический
маятник длиной l=
1 м и массой М = 5 кг и застревает в нем.
Определить угол отклонения маятника.
[ 18°30′ ]

3.5.
Зависимость потенциальной энергии
частицы в центральном силовом поле от
расстояния r
до

центра
поля задается выражением П(r)
=A/r²
-B/r,
где А
и
В —
положительные постоянные.

Определить
значение r₀,
соответствующее
равновесному положению частицы. Является
ли это положение положением устойчивого
равновесия? [r₀
= 2А/В]

3.6.
При центральном абсолютно упругом ударе
движущееся тело массой m₁
ударяется
в покоящееся тело массой m₂,
в результате чего скорость первого тела
уменьшается в n=
1,5 раза. Определить: 1) отношение m₁/m₂;
2)
кинетическую энергию T’₂,
с
которой начнет двигаться второе
тело, если первоначальная кинетическая
энергия первого тела T₁
=
1000 Дж. [ 1) 5; 2) 555 Дж ]

3.7.
Тело массой m₁=4
кг движется со скоростью v₁=3
м/с
и ударяется о неподвижное тело такой
же массы. Считая удар центральным и
неупругим, определить количество
теплоты, выделившееся при ударе. [9 Дж ]

* У. Гамильтон
(1805—1865) — ирландский математик и
физик.

Соседние файлы в папке Трофимова

Источник

Условие задачи:

Дано:

Решение задачи:

Ответ: 2,5 мДж.

Смотрите также задачи:

Введение

Импульс

Закон сохранения импульса

Работа и энергия

Механическая работа

Консервативные и диссипативные силы

Кинетическая и потенциальная энергия

Закон сохранения и изменения энергии

Теорема об изменении кинетической энергии

Соударения

Задача 1

Список литературы

Не пропустите также: