Как найти количество подведенной теплоты по графику

2.9.1 Определение количества подведенной теплоты цикла q1

Количество подведенной теплоты графически
определяется площадью под кривой
процесса.

После проведения подсчета количества
клеток под кривой оказалось 285 штук.

Масштаб одной клетки в координатах T-s:

• относительно оси T, K:
  30;

• относительно оси
  
  :
  14.

Следовательно, подведенная теплота
цикла, определенная графическим методом
равна:

2.9.2 Определение количества подведенной теплоты цикла q2

Количество отведенной теплоты графически
определяется площадью под кривой
процесса графика, изображающего весь
цикл. После проведения подсчета количества
клеток по графику оказалось, что всего
их 115 штук.

Масштаб одной клетки в координатах T-s:

• относительно оси T, K:
  30;

• относительно оси

  :
  14.

Следовательно, отведенная теплота
цикла, определенная графическим методом
равна:

Дж/кг

2.9.3 Определение количества теплоты цикла qc

Количество теплоты цикла определяет
площадь полученной в координатах T-s
фигуры. Чтобы определить эту площадь,
необходимо подсчитать количество клеток
внутри фигуры.

Масштаб одной клетки в координатах T-s:

• относительно оси T, K:
  30;

• относительно оси

  :
  14.

После проведения подсчета количества
клеток оказалось, что всего их 170 штук,
следовательно, теплота цикла, определенная
графическим методом равна:

Дж/кг

2.9.4 Определение количества работы цикла lc

Количество работы цикла определяет
площадь полученной в координатах p-v
трапеции. Чтобы определить эту площадь,
необходимо подсчитать количество клеток
внутри трапеции.

Масштаб одной маленькой клеточки в
координатах p-v:

• относительно оси р, Па: 100000;

• относительно оси v, м³/кг:
  0,021.

После проведения подсчета количества
клеток оказалось, что всего их 34 штуки,
следовательно, работа цикла, определенная
графическим методом равна:

Дж/кг

2.10 Сравнение значений
количества подведенной q₁
и отведенной q₂
теплоты, теплоты цикла q_c,
работы цикла l_c
цикла, полученных графическим методом,
с соответствующими величинами, полученными
при выполнении пункта 5

2.10.1 Определение
количества подведенной теплоты цикла
q₁

Графическим методом:

Дж/кг

Расчетным методом:

Дж/кг

Рассчитаем погрешность:

2.10.2 Определение
количества отведенной теплоты цикла
q₂

Графическим методом:

Дж/кг

Расчетным методом:

Дж/кг

Рассчитаем погрешность:

2.10.3 Определение
количества теплоты цикла q_c

Графическим методом:

Дж/кг

Расчетным методом:

Дж/кг

Рассчитаем погрешность:

2.10.4 Определение
количества работы цикла l_c.

Графическим методом:

Дж/кг

Расчетным методом:

Дж/кг

Рассчитаем погрешность:

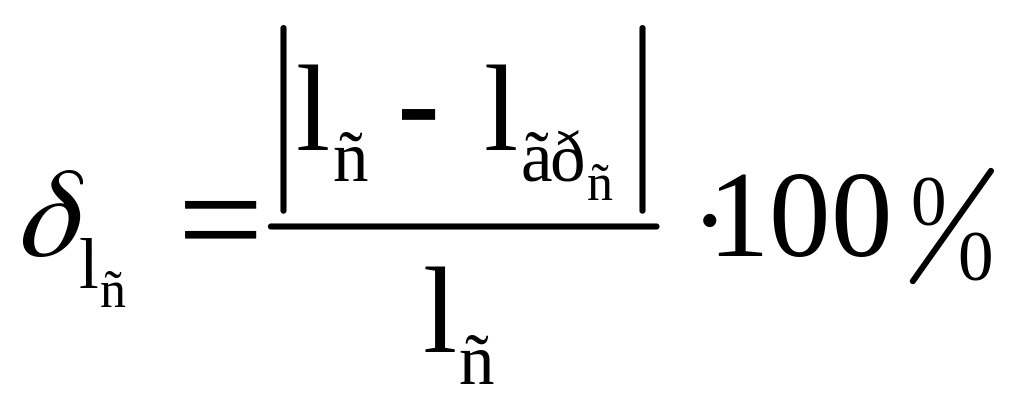
ГЛАВА
III.
РЕЗУЛЬТАТЫ РАСЧЕТОВ.

Таблица 3.1 — Параметры
состояния в характерных точках

Таблица 3.2 —
Характеристики термодинамических
процессов цикла

Таблица 3.3 —
Характеристики цикла

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Основными процессами в термодинамике являются:

• изохорный, протекающий при постоянном объеме;
• изобарный, протекающий при постоянном давлении;
• изотермический, происходящий при постоянной температуре;
• адиабатный, при котором теплообмен с окружающей средой отсутствует;
• политропный, удовлетворяющий уравнению pvⁿ= const.

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

• уравнение процесса в p—v иT—s координатах;
• связь между параметрами состояния газа;
• изменение внутренней энергии;
• величину внешней работы;
• количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.

Изохорный процесс

Изохорный процесс в p, v— , T, s— и i, s-координатах (диаграммах)

При изохорном процессе выполняется условие v = const.

Из уравнения состояния идеального газа (pv = RT) следует:

 p/T = R/v = const,

т. е. давление газа прямо пропорционально его абсолютной температуре:

 p₂/p₁ = T₂/T₁.

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

q= c_v(T₂ —  T₁). 

Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:

Δu = c_v(T₂ — T₁).

Изменение энтропии в изохорном процессе определяется по формуле:

s₂ – s₁= Δs = c_vln(p₂/p₁) = c_vln(T₂/T₁).

Изобарный процесс

Изобарный процесс в p, v— , T, s— и i, s-координатах (диаграммах)

Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

v/T = R/p = const

или

 v₂/v₁ = T₂/T₁,

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

l = p(v₂ – v₁). 

Т. к. pv₁ = RT₁ и pv₂ = RT₂, то

l = R(T₂ – T₁).

Количество теплоты при c_p = const определяется по формуле:

q = c_p(T₂ – T₁).

Изменение энтропии будет равно: 

s₂ – s₁= Δs = c_pln(T₂/T₁).

Изотермический процесс

Изотермический процесс в p, v— , T, s— и i, s-координатах (диаграммах)

При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

pv = RT = const

или

p₂/p₁ = v₁/v₂,

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

l  = RTln (v₂ – v₁) = RTln (p₁ – p₂).

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

q = l.

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

s₂ – s₁= Δs = Rln(p₁/p₂) = Rln(v₂/v₁).

Адиабатный процесс

Адиабатный процесс в p, v— , T, s— и i, s-координатах (диаграммах)

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

du + pdv = 0

или

Δu+ l = 0,

следовательно

Δu= —l. 

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq = 0 выразим следующим образом:

dq = c_адdT = 0. 

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад = 0).

Известно, что

с_p/c_v = k

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

pv^k = const. 

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).

Значения показателя адиабаты k для некоторых газов:

k_{воздуха} = 1,4

k_{перегретого пара} = 1,3

k_{выхлопных газов ДВС} = 1,33

k_{насыщенного влажного пара} = 1,135

Из предыдущих формул следует:

l= — Δu = c_v(T₁ – T₂);

i₁ – i₂= c_p(T₁ – T₂).

Техническая работа адиабатного процесса (l_техн) равна разности энтальпий начала и конца процесса (i₁ – i₂).

Адиабатный процесс, происходящий без внутреннего  трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.

Политропный процесс

Политропным называется процесс, который описывается уравнением:

pvⁿ= const.

Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:

p₂/p₁ = (v₁/v₂)ⁿ; T₂/T₁ = (v₁/v₂)^n-1; T₂/T₁ = (p₂/p₁)^(n-1)/n. 

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

q = (u₂ – u₁) + l.

Поскольку

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv⁰ = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p⁰v = const, p^1/∞v = const, pv^∞ = const – изохора;

pv^k = const (n = k) – адиабата.

n > 0 – гиперболические кривые,

n < 0 – параболы.

По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.

Графический
и табличный методы анализа тепловых процессов в задачах по физике.

Описаны
методы и приёмы, используемые автором в своей практической деятельности, при
изучении тепловых явлений в 8-м и 10-м классах. Примеры и иллюстрации, приведённые
в данном материале, позволяют продемонстрировать образцы решения задач по
термодинамике.

В
педагогической деятельности учителя физики приходится достаточно часто
сталкиваться с трудностями понимания учащимися анализа тепловых процессов. В
результате, казалось бы, простые задачи оказываются нерешенными. А ведь с
уравнением теплового баланса в курсе физики школьники встречаются дважды: в 8-м
и в 10-м классах, причём сложность изучения данной темы в старших классах
возрастает в разы. Но если в основной школе ученик не понял чего-то, то в 10-м
классе всё приходится начинать сначала.

При
поиске решения данных проблем нужно учитывать два важных параметра:

1.     
Методы
решения должны быть наглядными и универсальными;

2.     
Доступными
для понимания и применения большинству учащихся непрофильных классов.

Анализ
учебно-методической литературы и контрольно-измерительных материалов показал,
что графическое представление тепловых процессов позволяет значительно
упростить поиск решения и составление уравнений, а также выявить скрытые
процессы, т.е. обнаружить подводные камни. В статье представлено обобщение
опыта работы автора по теме «Тепловые явления»

Уравнение
теплового баланса. Изменение агрегатных состояний вещества

Многие
обучающиеся испытывают сложности при составлении уравнений для решения задач, в
которых происходит теплообмен между несколькими телами с учётом изменения
агрегатного состояния этих тел. Можно использовать схемы, отображать процессы с
помощью кругов, но, как выяснилось, все эти способы выраженного положительного
эффекта не дают.

Перед
тем как перейти к непосредственному рассмотрению приёмов решения задач по теме
«Тепловые явления», нужно отметить три важных замечания по методике изложения и
изучения данной темы:

1.     
Необходимо изначально показать обучающимся
важность составления и записи уравнения теплового баланса в общем виде:

2.     
Научить различать процессы,
сопровождающиеся выделением и поглощением теплоты, и подставлять в уравнение с
учётом отданного и полученного количества теплоты.

3.     
Научить читать
графики изменения температуры агрегатного состояния вещества.

Методика
решения подобных задач с учётом перехода из одного агрегатного состояния в
другое у каждого учителя своя, но любому учителю физики всегда важно рассмотреть
и альтернативную точку зрения. Плюсы и минусы своих вариантов всегда становятся
более заметными в сравнении с предложениями коллег.

Предлагаю
рассмотреть метод, состоящих всего из двух этапов:

1.     
Графическая интерпретация условия задачи.

2.     
Составление уравнения теплового баланса
для данной задачи, используя график, после чего начинается непосредственное
математическое решение задачи.

В
качестве примера рассмотрим несколько задач, начиная с самой простой с
постепенным усложнением. Обязательным условием в задачах будет наличие двух и
более тел.

Задача
№1 (без изменения агрегатных состояний веществ):

В
латунный калориметр массой 128 г, содержащий 240 г воды при температуре 8,4⁰С,
опущено металлическое тело массой 192 г, нагретое до 100⁰С. Окончательная
температура, установившаяся в калориметре, 21,5⁰С. Определите
удельную теплоёмкость испытуемого тела
[1].

Решение:

1.     
Графически показываем изменение
температуры всех тел, указанных в задаче. Видно, что в уравнении теплового
баланса будет три слагаемых. Для удобства можно записать уравнения для каждого
участка в отдельности:

2.     
Составляем уравнение согласно графику:

И
вот теперь начинается самое важное – математическое решение задачи.

На
первых же занятиях нужно обозначить целесообразность решения задачи в общем
виде. Показать на примерах, что решение по действиям веет к округлениям, и как
следствие – неправильному ответу. Ведь подстановка данных в выраженную из
формулы величину позволяет быстро и безошибочно получить верный результат.

Задача
№2 (с изменением агрегатных состояний веществ):

Смесь,
состоящую из 5 кг льда и 15 кг воды при общей температуре 0⁰С, нужно
нагреть до температуры 80⁰С пропусканием водяного пара при
температуре 100⁰С. Определить необходимое количество пара
[1].

Решение:

1.     
Графически показываем изменение
температуры всех тел, указанных в задаче. Видно, что в уравнении теплового
баланса будет пять слагаемых. Для удобства можно записать уравнения для каждого
участка:

2.     
Составляем уравнение согласно графику:

Задача
№3 (с изменением агрегатного состояния части одного из веществ):

В
бак, содержащий воду массой 10 кг при температуре 20⁰С, бросили
кусок железа массой 2 кг, нагретый до температуры 500⁰С. При этом
некоторое количество воды превратилось в пар. Конечная температура,
установившаяся в баке, равна 24⁰С. Определить массу воды,
обратившейся в пар [1].

Решение:

1.     
Графически показываем изменение
температуры всех тел, указанных в задаче. Видно, что в уравнении теплового
баланса будет четыре слагаемых. Для удобства можно записать уравнения для
каждого участка:

2.     
Составляем уравнение согласно графику:

 Данный
метод позволяет наглядно увидеть, что происходит в задаче с веществами и какие
уравнения необходимы для решения задачи.

Первый
закон термодинамики для изопроцессов и КПД тепловой машины.

Данная
тема при своей простоте, вызывает серьёзные затруднения у выпускников при
решении задач 28 и 30 части 2 ЕГЭ по физике.

Так
же, как и в предыдущем случае, предлагаемый метод предполагает выполнение
следующих задач:

1.     
Научить обучающихся анализировать графики
тепловых процессов для начала с помощью таблицы (для начала).

2.     
Быстро определять в различных осях
координат (p,V,T)
максимальные и минимальные значения температуры, давления и объёма газа.

3.     
Использовать уравнение Клапейрона-Менделеева
для выражения внутренней энергии или работы газа через другие величины.

4.     
Научить определять работу газа на участке
как площадь фигуры под ним в координатах p(V).

Все
эти навыки отрабатываются на каждом уроке в течение всего процесса изучения
молекулярной физики газов. Необходимый уровень навыков достигается в течение
нескольких занятий, после чего данный метод решения ложится в основу обобщения
изученных приёмов и при подготовке к ЕГЭ ученик уже имеет необходимые знания и
навыки, что позволяет сконцентрироваться на более детальном рассмотрении задач
повышенной сложности.

Метод
анализа тепловых процессов с позиции термодинамики состоит из двух этапов:

1.     
Анализ замкнутого цикла и заполнение расширенной
таблицы.

2.     
Составление необходимых соотношений,
уравнений согласно условия задачи с опорой на анализ.

Рассмотрим
по аналогии с предыдущими задачами несколько типовых задач по термодинамике,
применив к ним данный метод решения.

Задача
№1 (определение участков, где выделялась или поглощалась теплота):

Определите
на каком участке графика газу сообщалась теплота и вычислите её значение?

Решение:

1.     
Анализируем график и заполняем таблицу. Из
таблицы видно, на каких участках к системе подводилась теплота, а на каких
отводилась. В дальнейшем можно подвести учащихся к осознанию того, что и без
таблицы можно быстро определять, что теплота подводится на тех участках где
происходит увеличение температуры или объёма газа. Однако надо быть аккуратным
с таким утверждением и помнить об адиабатном расширении или сжатии, т.к. в
таком случае никакого теплообмена не происходит.

2.     
Из таблицы выводим уравнение для расчёта
количества теплоты, поступившей от нагревателя или наоборот отдаваемой в
окружающую среду:

Для
решения задачи остаётся лишь воспользоваться изученным уравнениями. По поводу
возможного замечания о том, что при передаче теплоты холодильнику в уравнении
должен быть знак «минус», можно ответить, что он появится автоматически, если
ученик будет правильно выполнять расчёт изменения внутренней энергии и работы
газа. Необходимо помнить, что при вычислении любого изменения необходимо
отнимать начальное значение от конечного, это же касается расчёта работы газа
как площади фигуры по графику процесса в осях p(V).

Задача
№2 (определение изменения каких-либо макропараметров):

Как
изменялась температура газа на каждом участке? Опишите процессы, происходящие с
газом.

Решение:

Анализируем
график и заполняем таблицу. Из таблицы видно, как менялась внутренняя энергия и
количество теплоты, на основании табличных данных делается описание процессов и
изменение температуры.

Задача
№3 (расчёт КПД тепловой машины):

Определите
КПД тепловой машины.

Решение:

1.     
Полезную работу газа по данному графику
определить очень просто, она равна площади фигуры цикла. А вот количество
теплоты, подводимой к системе определить можно двумя способами. Самый быстрый –
посмотреть на каких участках было увеличение температуры и объёма. Из графика
видно, что изотерма, проходящая через точку 2 выше чем изотермы, проведённые
через точки 1 и 3. А изотерма в точке 1 ниже чем в точке 3. Участок 2-3
изохорный процесс, поэтому количество теплоты сообщалось только на участке 1-2.
К данному выводу, можно прийти и через таблицу:

2.     
Составляя уравнение КПД необходимо
записать выражения изменения внутренней энергии и работы газа через p₀
и V₀,
тогда они сократятся и останется только числовое выражение.

Данная
методика позволяет анализировать более сложные задачи и находить нюансы которые
могут быть упущены при беглом просмотре условия задачи. Рассмотрим пример такой
задачи.

Задача
№4 (расчёт КПД тепловой машины):

Определите
КПД тепловой машины.

Решение:

Данная
задача может показаться простой для ученика, но в ней есть один важный момент.
При расчёте количества теплоты сообщаемой нагревателем, необходимо рассчитать
положительное изменение внутренней энергии. А на данном графике, не каждый
ученик сможет увидеть, что на участке 1-2 было увеличение температуры. Большая
часть учащихся увидев данный участок, воспользовавшись уравнением состояния
идеального газа обнаружит, что температура в точке 2 меньше температуры в точке
1, а значит было уменьшение внутренней
энергии и не станут учитывать её изменение на этом участке. На самом же деле,
мы имеем дело с процессом, где температура меняется по нелинейному закону
(квадратичная зависимость). Температура увеличивалась от
точки 1 до точки М. После чего начиналось уменьшение внутренней энергии. Таким
образом количество теплоты полученной от нагревателя будет определяться как:

Заполняя
таблицу, ученики не проводя вышеописанного анализа, столкнулись бы с вопросом,
как заполнить ячейку количества теплоты на участке 1-2, это послужило бы для
них сигналом, что необходим детальный анализ данного участка.

Дальнейшие
действия по решению данной задачи выходят за рамки темы статьи. Заметим, что
здесь необходимо использовать знания из математики о линейной функции, участком
которой является отрезок 1-2. Получив функциональную зависимость давления от
объёма на этом участке, необходимо подставить её в уравнение
Клапейрона-Менделеева и задача будет решена.

Приведенные
выше методы решения задач на тепловые являения, при должном усердии и
кропотливой работе учителя над формированием необходимых умений у обучающихся
позволяют подготовить учеников к решению более сложных задач по тепловой физике
и нивелировать их страх перед сдачей выпускного экзамена по физике. Но главным
является то, что использование этих приёмов приводит к развитию нестандартного,
творческого мышления школьника, независимо от профиля его обучения.

Надеемся,
что предложенные приёмы решения задач по термодинамике помогут сделать изучение
тепловых процессов более простым и понятным, будут способствовать формированию
исследовательских навыков при решении задач и окажут положительное воздействие
на интеллектуальное развитие школьников.

Список
использованной литературы

1.     
Кирик, Л.А. Физика-8. Разноуровневые
самостоятельные и контрольные работы. – Харьков.: «Гимназия», 2001. –
144 с.

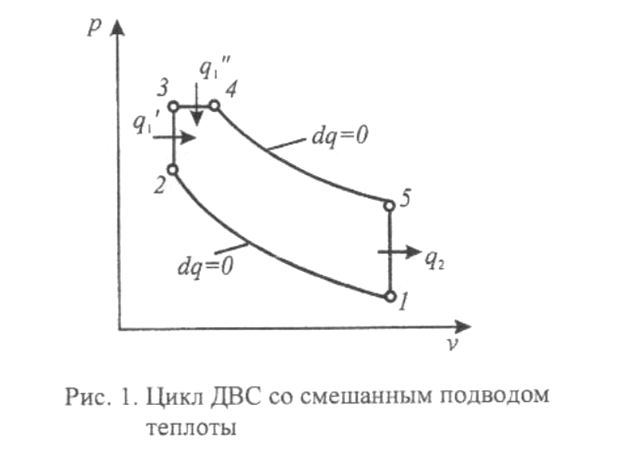
Задача 214

Условие: Для теоретического цикла ДВС со смешанным подводом теплоты, смотри рисунок 1, определить количество подведенной теплоты q1 , количество отведенной теплоты q2, полезную работу цикла lц, и термический КПД цикла ηt,. Определить также, КПД цикла Карно, имеющего одинаковые с заданным циклом минимальную и максимальную температуры. Параметры рабочего тела в начале процесса сжатия: давление – р1=0,1 МПа; начальная температура – t1= -14º С. Заданы безразмерные характеристики цикла: степень сжатия – ε=v1/v2=22; степень повышения давления – λ=р3/р2=1,7; степень предварительного расширения – ρ=v3/v4=1,7. В одном килломоле рабочего тела содержится: 0, 73 кмоль N2; 0, 05 кмоль О2; 0, 04 кмоль CО2; остальное – H2О (т.е. состав смеси задан мольными долями).
Указания (порядок выполнения расчетов):
1. Рассчитать молекулярную массу, газовую постоянную, теплоемкости Cp и Cv газовой смеси, а также показатель адиабаты к. Считать их постоянными для всего цикла. 2. Определить для характерных точек цикла значения давления р, температуры Т, удельного объема v, энтальпии h, и энтропии s. Результаты свести в таблицу.
3. Рассчитать количество подведенной q1 и отведенной q2 теплоты, работу цикла lц, изменение энтальпии, внутренней энергии и энтропии для всех процессов, образующих цикл. Результаты свести в таблицу.
4. Определить термический КПД заданного цикла ηt, а также КПД цикла Карно, имеющего одинаковые с заданным циклом минимальную и максимальную температуры.
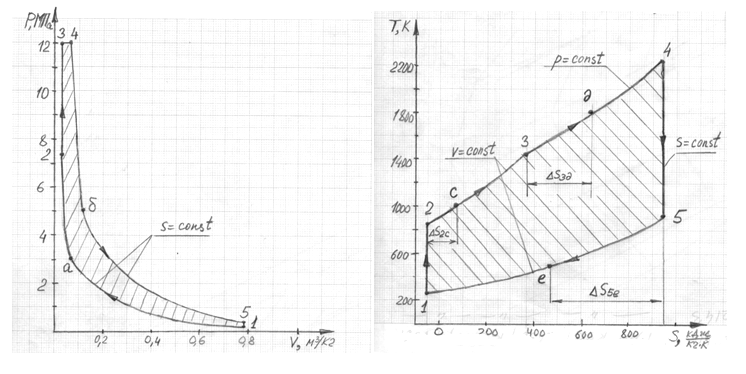
5. По результатам расчетов изобразить цикл ДВС на миллиметровой бумаге в масштабе в координатах р-v и T-s. Величину энтропии определить относительно состояния при нормальных физических условиях (Т0=273 К, р0=0,101 МПа). При изображении процессов кривыми линиями определить параметры, по крайней мере, одной промежуточной точки.

Первый закон термодинамики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

к оглавлению ▴

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние (рис. 1).

Рис. 1.

Работа газа равна:

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

(1)

Если и — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма до объёма . С помощью аналогичных рассуждений приходим к формуле:

Но , и снова получается формула (1).

Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

к оглавлению ▴

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу . Тогда работа газа во всём процессе найдётся суммированием этих малых работ:

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь

к оглавлению ▴

Работа, совершаемая над газом

Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу , которую поршень совершает над газом.

Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой , равной силе по модулю и противоположной по направлению: (рис. 4).

Рис. 4. Внешняя сила , действующая на газ

Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:

Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:

(2)

Нас больше всего интересует случай, когда тело является газом. Тогда (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или

(3)

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

к оглавлению ▴

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:

Всё подведённое к газу тепло идёт на совершение газом работы.

2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:

к оглавлению ▴

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе . Из первого закона термодинамики получаем: , или .

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет , поэтому : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.